Simulating Surface Aeration Systems at Different Scale of Mixing Time*
Achanta Ramakrishna Rao and Bimlesh Kumar
?
Simulating Surface Aeration Systems at Different Scale of Mixing Time*
Achanta Ramakrishna Rao and Bimlesh Kumar**
Department of Civil Engineering, Indian Institute of Science, Bangalore-12, India
Macro and micromixing time represent two extreme mixing time scales, which governs the whole hydrodynamics characteristics of the surface aeration systems. With the help of experimental and numerical analysis, simulation equation governing those times scale has been presented in the present work.
mass transfer, macromixing, micromixing, surface aerators, theoretical power per unit volume, rotor speed
1 INTRODUCTION
The activated-sludge process is one of the most popular processes used to treat domestic and industrial wastewaters. To produce an improved effluent quality by removing substances that have a biological oxygen demand, the aeration system in the activated-sludge process must supply enough oxygen to maintain the metabolic reactions of the microorganisms and provide sufficient mixing in the aeration tank [1]. The aeration system represents the most energy-intensive operation unit in the activated sludge process. Therefore, many different types of aeration systems have been developed over the years in an effort to improve the energy efficiency of aeration. Surface aerators are a popular choice of aeration system because of their inherent simplicity and reliability and their competitive rate of oxygen transfer per unit of power input under actual mixed-liquor aeration conditions [2].
Mixing is an important operation in surface aeration systems. The efficiency of the aeration system is dependent on the mixing conditions. Mixing is an important issue to be considered during the scale-up of many processes, particularly those involving batch reactors like surface aeration systems.
The objective of doing studies on aeration process is to interpret the laboratory result into the filed installation. This means scaling up of laboratory geometric dimensions for the field installation. It requires a geometrical similarity condition that is to say that the field installation should be built on a definite geometric ratio of the laboratory setup. “Scale-up” is an inherent part of process development. Using the definition given by Bisio and Kabel [3], scale-up can be defined as: “the successful startup and operation of a commercial unit whose design and operation procedures are in part based upon experimentation and demonstration at a smaller scale of operation”.
The process of turbulence mixing is very complex. Mixing mechanisms can be grouped into three main categories depending on their characteristic length scale. Small scale mixing close to the molecular level is referred to as micromixing; macromixing is mixing on a large scale, and intermediate scale mixing is called mesomixing. Hence, the understanding of the mixing characteristics is highly desirable in surface aeration systems.
A contribution toward providing a more fundamental approach was made by Bourne and his colleagues through the development of both an experimental technique and an accompanying mathematical model for characterizing what is termed “micromixing” [4, 5]. In Refs. [6-10], different types of models have been proposed to describe mixing processes. In most cases, small-scale mixing mechanisms are characterized with simplified mechanistic models such as the E-model [11, 12], whereas macromixing is described by simplified models. Mixing-precipitation models, which use a detailed characterization of the macromixing,have also been used [7, 8], but in these cases, small scale mixing effects are neglected, thus the multiscale nature of the process is not modeled in all details. However, it has been shown that accounting for such effects can be crucial to capture correctly the system behavior [13]. Unlike macromixing which is associated with large-scale fluid motions that can be monitored directly through physical property measurements, micromixing deals with diffusive mixing on the molecular level and only indirect methods are available for measuring it [5, 14, 15]. In spite of such availability of literature on mixing length scale, typically on mixing scale behavior of surface aerators is missing.
Present work does an attempt of understanding the mixing scale prevalent in surface aeration systems and also tries to find the scale up or simulation equation for different mixing scale.
2 MIXING SCALE IN SURFACE AERATION SYSTEMS
The mixing process is divided into macromixing, mesomixing, and micromixing. These mixing stages complement each other in the sense that they describe different scales of mixing. The mixing stages may occur one after the other or simultaneously. For a process carried out in a stirred tank, the largest scale of mixing is the scale of the whole reactor. Macromixing determines the environment concentrations for mesomixing and micromixing and conveys fluids that are undergoing meso and micromixing through environments where the turbulence properties vary. Macromixing refers to flow processes controlling the residence time distribution,.. the mean convective flow in the vessel. Macromixing can be characterized by the circulation timem, which can be estimated as:
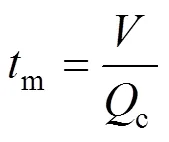
The characteristic time-scale for mesomixing (s) by inertial convective mechanisms can be estimated as Ref. [16]:
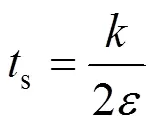
whereis the turbulent kinetic energy, andis the energy dissipation rate.
Micromixing is mixing on the smallest scales of motion and at the final scales of molecular diffusivity. An important feature of micromixing (m) is the accelerating effect of viscous convective deformation on molecular diffusion.mis estimated as follows:
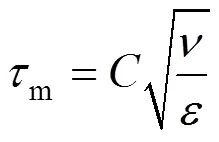
whereis a constant, andis the kinematic viscosity.
Mesomixing is used to describe a set of phenomena between macromixing, which involves the whole vessel, and micromixing, which involves a small volume at the smallest eddy scales. So in designing a surface aeration systems or simulating surface aeration systems, it is imperative to know the behavior of these extreme scales.
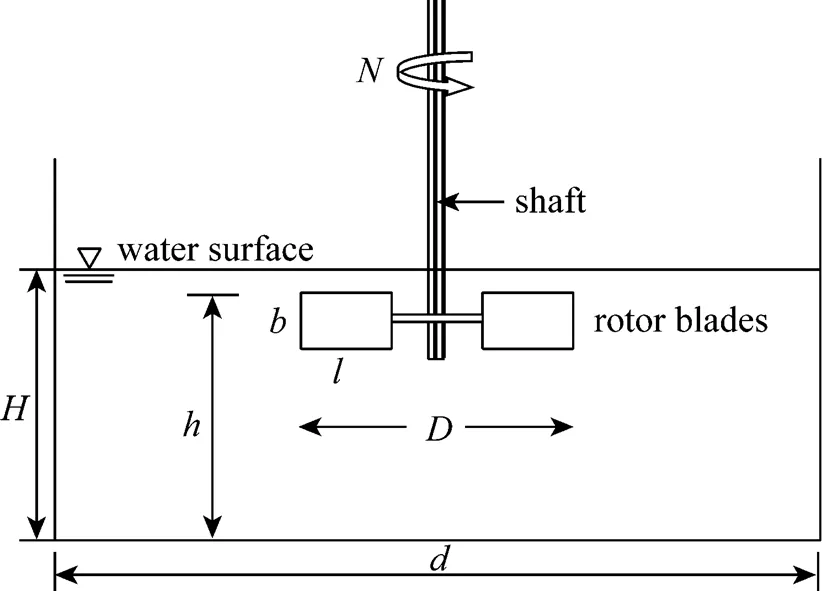
Figure 1 Schematic representation of a surface aeration tank
3 CALCULATIONS OF PROCESS PARAMETERS
Calculations have been carried out on two sizes (0.5184 m2and 1 m2) of circular surface aerators. A schematic representation of the aerator is shown in Fig. 1. The rotor is fitted with six flat blades Rushton turbines. The geometric similarity conditions [Eq. (4)] given by Udaya. [17] is maintained in the aerators.
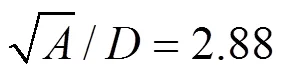
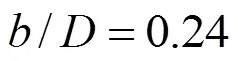
Where,is the cross-sectional area of the tank,is the depth of water in the tank,is the diameter of the rotor and the distance between the top of the blades, and the horizontal floor of the tank isand,are the linear dimensions of the blade. Experimental work is performed to get the mass transfer coefficients. Calculation of mass transfer coefficients (Ka20) have been based on two-film theory [18], and it is calculated for each rotational speed in both the tanks.
According to two-film theory [18], the oxygen transfer coefficient at°C,Kamay be expressed as follows:
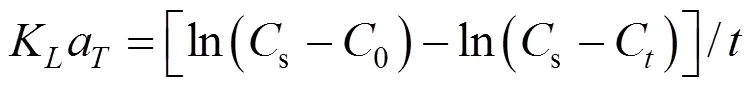
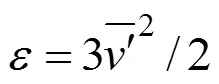
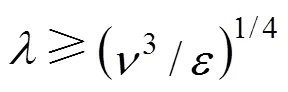
Inside such and smaller elements, the mixing is mainly caused by molecular diffusivity. In a mixing tank, there are two characteristic values of the scale:
(1) Maximum microscale,bulkfor the bulk of flow estimated according to Eq. (7), with the average turbulent dissipation value in the bulk estimated as
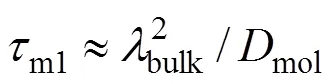
wherebulkis linear scale of turbulence in bulk volume, andmolis the molecular diffusivity.
(2) Minimum microscale,mfor area with the highest local dissipationmwith characteristic micromixing time
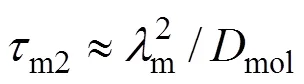
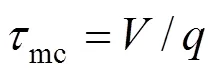
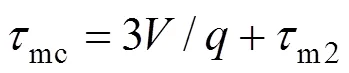
There are, thus, two independent estimates of the micromixing time:m1andmc. The lower of the two is selected by the program as the micromixing time;m. Calculation of micromixing time has been carried out on different rotational speeds.
4 ANALYSES OF THE RESULTS
In this section, experimental and numerical results obtained by Visimix?[20] for macro and micromixing time are analyzed in order to present simulation equations for both of them in geometrically similar surface aeration systems.
4.1 Macromixing time (tm)
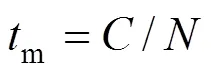
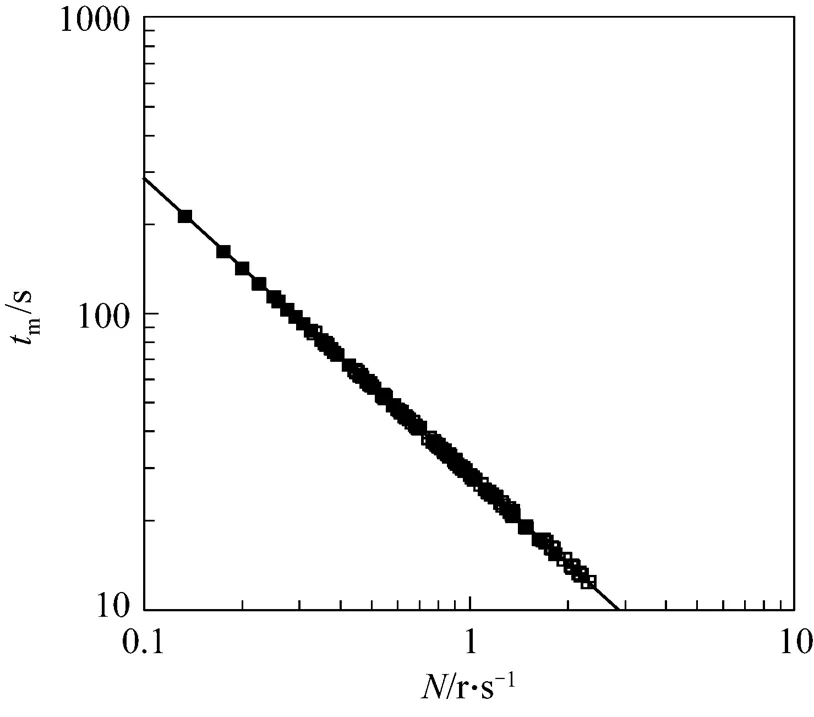
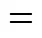
4.2 Micromixing time (τm)
Micromixing is the limiting step in the progress of fast reactions because micromixing dramatically accelerates the rate of production of interfacial area available for diffusion. Micromixing time can provide useful information about the performance of the surface aeration tanks. Micromixing time takes into consideration the small eddies responsible for the concentration gradients surrounding. Numerical data of micromixing time has been plotted in the Fig. 3 with rotor speed as in the case of macromixing time.
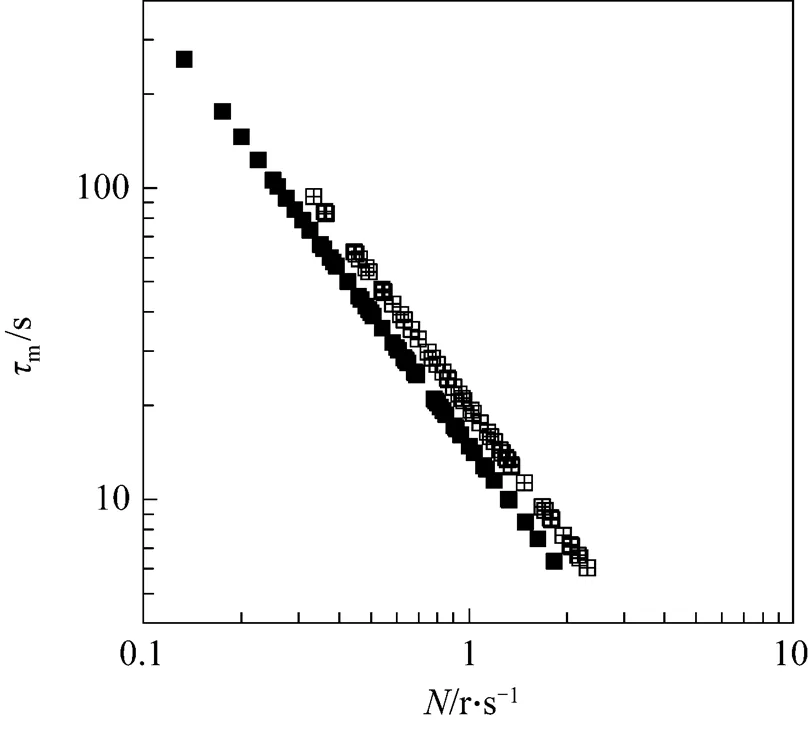

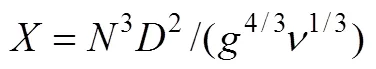
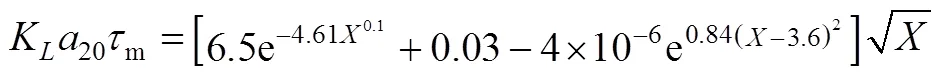
With the help of equation simulatingKa20with[19], we can get values ofmat individual rotor speed.

Oxygen transfer in surface aeration tanks can be explained by coupling the effects of the two most important scales of mixing inside it, the micromixing scale and the macromixing scale. Each mixing scale has a particular effect on the oxygen transfer rate. Macromixing accounts for the geometrical configuration of the surface aerator, where the scaled up problems are focused. In the present work, simulation equation for macro and micromixing time in surface aeration systems has been presented. These equations can be used in scaling up the process characteristics of surface aeration systems.
NOMENCLATURE
cross-sectional area of the tank, m2
blade width of the rotor
a constant
ssaturation value of dissolved oxygen at test conditions
Cconcentration of dissolved oxygen at any time
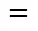
1a constant depending on the pumping capacity of the impeller
impeller diameter
molmolecular diffusivity
depth of water in the tank
distance between the top of the blades and the horizontal floor of the tank
Ka20mass transfer coefficient
blade length of the rotor
stirring rate, r·s-1
ccirculation capacity
circulation
mmacromixing time, s
smesomixing time, s
liquid volume in the tank
mmicromixing time, s
1 Chern, J.M., Yang, S.P., “Oxygen transfer rate in a coarse-bubble diffused aeration system”,...., 42, 6653-6660 (2003).
2 McWhirter, J.R., Chern, J.M., Huttefi, J.C., “Oxygen mass transfer fundamentals of surface aerators”,...., 34, 2644-2654 (1995).
3 Bisio, A., Kabel, R.L., Scale-up of Chemical Processes-Conversion of Laboratory Scale Tests to Successful Commercial Size Design, John-Wiley & Sons (1995).
4 Bourne, J.R., Kozicki, F., Rys, P., “Mixing and fast chemical reaction (I) Test reactions to determine segregation”,..., 36, 1643 (1981).
5 Angst, W., Bourne, J.R., Sharma, R.N., “Mixing and fast chemical reaction (IV) The dimensions of the reaction zone”,..., 37, 585 (1982).
6 Podgorska, W., “Influence of micromixing on precipitation”, Ph.D. Thesis, Warsaw University of Technology (1993).
7 Wei, H., Wei, Z., Garside, J., “Computational fluid dynamics modeling of the precipitation process in a semibatch crystallizer”,...., 40, 5255-5261 (2001).
8 Jaworski, Z., Nienow, A.W., “CFD modelling of continuous precipitation of barium sulphate in a stirred tank”,..., 91, 167-174 (2003).
9 Vicum, L., Ottiger, S., Mazzotti, M., Makowski, L., Ba?dyga, J., “Multiscale modeling of a reactive mixing process in a semibatch stirred tank”,..., 59, 1767-1781 (2004).
10 Kresta, S., Anthieren, G., Parsiegla, K., “Model reduction for prediction of silver halide precipitation”,..., 60, 2135-2153 (2005).
11 Ba?dyga, J., Bourne, J.R., “Simplification of micromixing calculations (I) Derivation and application of new model”,..., 42, 83–92 (1989).
12 Phillips, R., Rohani, S., Ba?dyga, J., “Micromixing in a single-feed semi-batch precipitation process”,., 45, 82-92 (1999).
13 Ba?dyga, J., Orciuch, W., “Barium sulphate precipitation in a pipe—An experimental study and CFD modeling”,..., 56, 2435–2444 (2001).
14 Villermaux. J., David, R., “Recent advances in the understanding of micromixing phenomena in stirred reactors”,..., 21, 105 (1983).
15 Rice, R.W., Baud, R.E., “The role of micromixing in the scale-up of geometrically similar batch reactors”,., 36 (2), 293-298 (1990).
16 Ba?dyga, J., Bourne, J.R., Turbulent Mixing and Chemical Reactions, Wiley, Chichester (1999).
17 -Udaya, S.L., Shrma, K.V.N.S., Rao, A.R.K., “Effect of geometrical parameters for overall oxygen transfer coefficient”, In: Proc. Symp. on Environmental Hydraulics, University of Honking (1991).
18 Metcalf & Eddy Inc., Waste Water Engineering: Treatment Disposal and Reuse, Tata McGraw-Hill, New Delhi (2004).
19 Rao, A.R.K., Laxmi, B.V.B., Narasiah, K.S., “Simulation of oxygen transfer rates in circular aeration tanks”,..., 39 (3), 237-244 (2004).
20 Rao, A.R.K., Kumar, B., “Scaling-up the geometrically similar unbaffled circular tank surface aerator”,..., 31 (2), 287-293 (2008).
21 Rao, A.R.K., “Prediction of reaeration rates in square, stirred tanks”,...,, 125 (3), 215-233 (1999).
22 Rao, A.R.K., Kumar, B., “Rectangular tank surface aerators: scale-up criteria and energy conservation”,....., 3 (4), 427-435 (2006).
23 Rao, A.R.K., Kumar, B., “Scale-up criteria of square surface aerators”,.., 96 (3), 464-470 (2007).
2008-04-14,
2009-02-17.
the Department of Science and Technology, Government of India (DSTO717).
** To whom correspondence should be addressed. E-mail: bimk@civil.iisc.ernet.in
 Chinese Journal of Chemical Engineering2009年2期
Chinese Journal of Chemical Engineering2009年2期
- Chinese Journal of Chemical Engineering的其它文章
- Design and Performance Analysis of Micro Proton Exchange Membrane Fuel Cells*
- Isolation of Cordyceps ophioglossoides L2 from Fruit Body and Optimization of Fermentation Conditions for Its Mycelial Growth*
- Efficient and Comprehensive Utilization of Hemicellulose in the Corn Stover*
- Kinetics of Reaction-Crystallization of Struvite in the Continuous Draft Tube Magma Type Crystallizers—Influence of Different Internal Hydrodynamics
- Preparation and Characterization of Tungsten-substituted Molybdophosphoric Acids and Catalytic Cyclodehydration of 1,4-Butanediol to Tetrahydrofuran*
- Facile Preparation of Danazol Nanoparticles by High-Gravity Anti-solvent Precipitation (HGAP) Method*
