吳永鋒

(銅陵學(xué)院數(shù)學(xué)與計算機科學(xué)系,安徽銅陵 244000)

NA列與兩兩NQD列的Lp收斂性

吳永鋒

(銅陵學(xué)院數(shù)學(xué)與計算機科學(xué)系,安徽銅陵 244000)

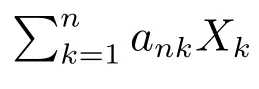
NA列;兩兩NQD列;Lp收斂性;一致可積

1 引言

定義1稱隨機變量X和Y是NQD(Negatively Quadrant Dependend)的,若對任意x,y∈R都有

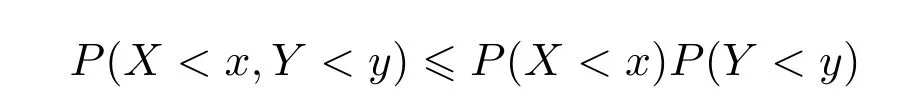
稱隨機變量序列{Xn,n≥1}是兩兩NQD列,若對任意i/=j,Xi與Xj是NQD的.

定義2稱隨機變量X1,X2,…,Xn,n≥2是負相關(guān)(Negatively Associated,簡記為NA) 的,若對{1,2,…,n}的任意兩個非空不相交子集A1與A2均有

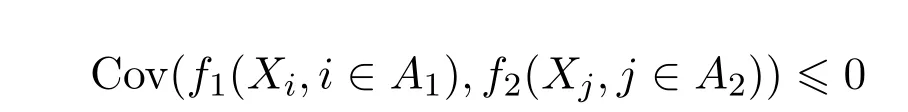
其中fi,i=1,2是使上式有意義且對各變元非降(或同時對各變元非升)的函數(shù).稱隨機序列{Xn,n≥1}是NA的,如果對任意n≥2,X1,X2,…,Xn是NA的.

兩兩NQD列的概念是由Lehmann[1]于1966年提出的,而NA列則是由Joag-Dev 和Proschan[2]于1983年提出.近年來關(guān)于這兩種序列的極限理論獲得了迅猛發(fā)展,如文[3-6] 等.

稱隨機序列{Xk,k≥1}是p階Ces`aro一致可積的[7](p＞0),若

文[4-5]分別在(1)式的條件下獲得了NA列與兩兩NQD列的Lp收斂性結(jié)果.本文則在下述更弱的條件下推廣文[4-5]中的結(jié)果.

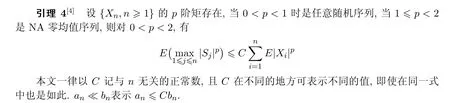
2 主要結(jié)果及證明

引理5{Xn,n≥1}是任意隨機序列,{ank;1≤k≤n,n∈N}是實數(shù)陣列,p＞0,若(4)式成立,且=

[1]Lehmann E L.Some concepts of dependence[J].Ann.Math.Statist.,1966,37:1137-1153.

[2]Joag-Dev K,Proschan F.Negative association of random variableswith app lications[J].Ann.Statist.,1983, 11:286-295.

[3]吳永鋒.兩兩NQD列的Lp收斂性和完全收斂性[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2008,24(3):605-609.

[4]吳群英,王遠清,伍艷春.NA陣列行和最大值的若干極限定理[J].應(yīng)用概率統(tǒng)計,2006,22(2):56-62.

[5]萬成高.兩兩NQD列的大數(shù)定律和完全收斂性[J].應(yīng)用數(shù)學(xué)學(xué)報,2005,28(2):253-261.

[6]吳群英.兩兩NQD列的收斂性質(zhì)[J].數(shù)學(xué)學(xué)報,2002,45(3):617-624.

[7]Chandra T K.Uniformintegrability in the Ces`aro sence and theweak law of large numbers[J].Sankhya:the Indian Yournal of Statistics,1989,51(series A):309-317.

[8]Ord′o?nez Cabrera M.Convergence ofweighted sum s of random variables and uniformintegerbility concerning the weights[J].Collect M ath.,1994,43:121-132.

Lpconvergence for NA random sequences and pairwise NQD random sequences

WU Yong-feng

(Departm ent of Mathem atics and Com puter Science,Tongling University,Tongling 244000,China)

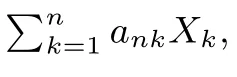
NA random sequences,pairw ise NQD random sequences,Lpconvergence,uniformintegrability

O211.4

A

1008-5513(2009)02-0377-07

2008-10-04.

安徽高校省級自然科研項目(KJ2008B 15ZC),安徽省高校青年教師資助計劃項目(2008jq1140).

吳永鋒(1977-),碩士,研究方向：概率極限理論.

2000M SC:60F15