于林,殷櫻

(三峽大學(xué)理學(xué)院,湖北宜昌 443002)

鞅空間的原子分解與有限鞅的稠密性

于林,殷櫻

(三峽大學(xué)理學(xué)院,湖北宜昌 443002)

引入了原子鞅與正則原子鞅概念,并研究了兩類Banach空間值鞅Hardy空間的原子分解和有限鞅的稠密性,所得結(jié)論揭示了鞅Hardy空間正則原子鞅分解的存在性,有限鞅的稠密性和Banach空間的一致光滑性(或一致凸性)三者之間的內(nèi)在聯(lián)系.

鞅空間;原子分解;有限鞅;稠密

1 概念與引理

設(shè)(?,F,P)是完備的概率空間,(X,‖·‖)是Banach空間,設(shè)f={fn}n≥0是關(guān)于F的某個遞增子σ-代數(shù)序列{Fn}n≥0適應(yīng)的X值鞅,記df={dfn}n≥0是f的鞅差序列,其中dfn=fn?fn?1, n≥0,令f?1≡0,F?1={φ,?}.?p:0＜p＜∞,定義鞅的極大函數(shù)和p階均方函數(shù)如下

上述鞅空間的引入和有關(guān)背景的討論,實值鞅情況可參見文[1-2],向量值鞅情況可參見文[3-9].

2 原子分解

定義4設(shè)X是Banach空間,1＜p＜∞,1≤r＜∞,X值鞅a={an}n≥0稱為是A1(r,∞)(或A2(r,p,∞))原子鞅,若存在停時τ使得

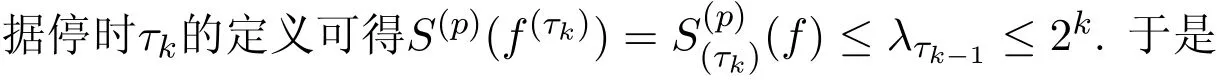
3 有限鞅的稠密性

下面討論鞅空間的原子分解,有限鞅的稠密性與Banach空間的一致光滑性(或一致凸性)之間的聯(lián)系.有限鞅在向量值鞅空間中稠密性的某些討論和應(yīng)用可參見文[9].

定義8[9]稱過程f={fn}n≥0為有限鞅,若fn=E(f|Fn),n≥0,且存在n0使得f是Fn0可測.

注由定義知有限鞅均具有形式:f={f1,f2,…,fn0,fn0,…}.

定理3設(shè)X是Banach空間,1＜p≤2,1≤r≤p,則下列條件等價:

(1)X同構(gòu)于p一致光滑空間;

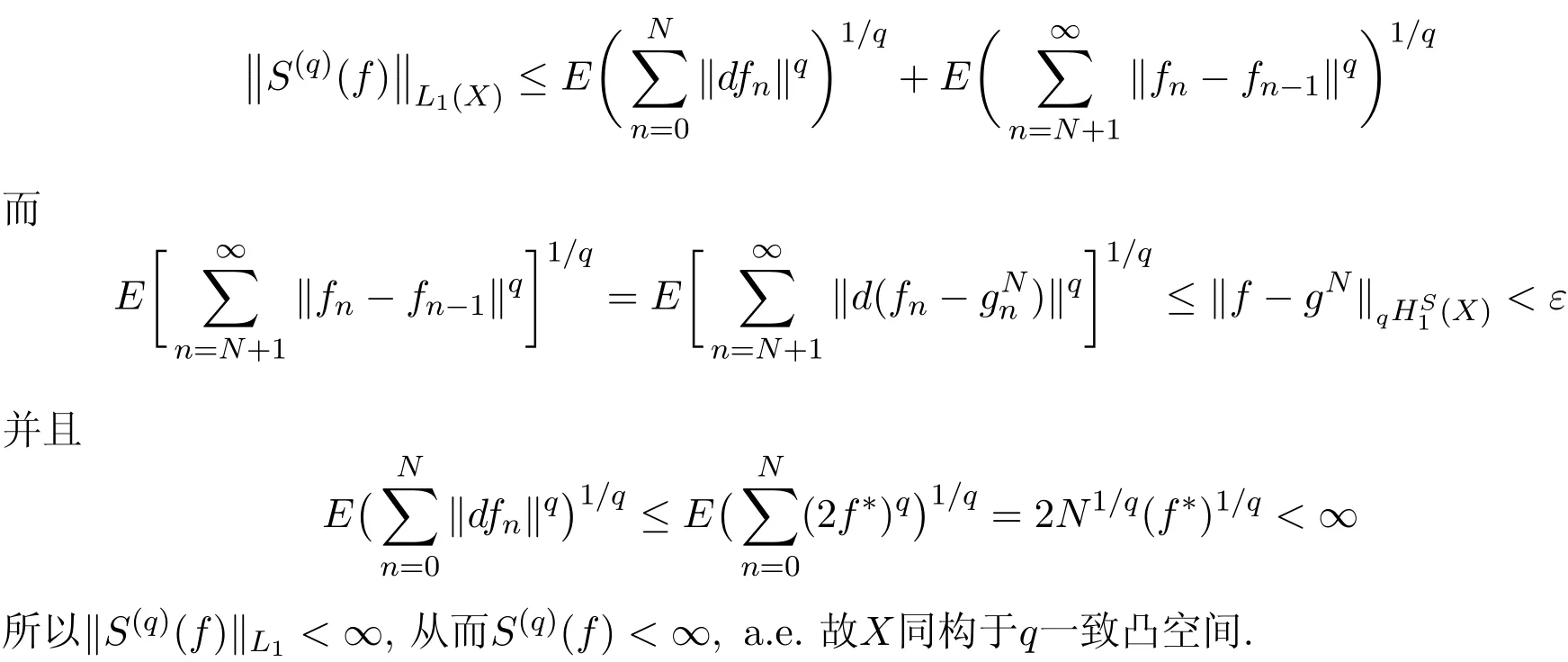
[1]Long Ruilin.Martingale Spaces and Inequalities[M].Beijing:Peking University Press,Vieweg Publishing, 1993.

[2]Weisz F.Martingale Hardy Spaces and Their Applications in Fourier Analysis Lecture Notes in Mathematics(1568)[M].Berlin Heidelberg:Springer-Verlag,1994.

[3]劉培德.鞅與Banach空間幾何學(xué)[M].北京：科學(xué)出版社,2007.

[4]于林.向量值鞅空間理論[M].北京：北京理工大學(xué)出版社,2005.

[5]于林.Banach空間中的Rodenthal型不等式及其應(yīng)用[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2007,23(1):4-10.

[6]劉培德,于林.小指標(biāo)B值鞅空間與原子分解[J].中國科學(xué):A輯,2001,31(17):615-625.

[7]于林.平削算子生成的B值鞅空間及其原子分解[J].應(yīng)用數(shù)學(xué),2004,17(1):108-114.

[8]于林,劉培德.向量值鞅Lipschitz空間pΛβ(X)和pλβ(X)[J].數(shù)學(xué)學(xué)報,2001,44(1):59-68.

[9]Mart′?nez T,Torrea J L.Boundedness of vector-valued martingale transforms on extreme points and applications[J].J.Aust.Math.Soc.,2004,76:207-221.

Atomic decompositions and density of finite martingales in martingale spaces

YU Lin,YIN Ying
(Science College,China Three Gorges University,Hubei,Yichang443002,China)

The concepts of atomic martingales and regular atomic martingales are introduced,then the atomic decompositions and the density of finite martingales in two classes of Banach-space-valued martingale Hardy spaces are investigated.By the results obtained here,the internal relations among the existence of atomical decompositions,the density of finite martingales and the uniform smoothness(or uniform convexity)of Banach spaces are exposed.

martingale space,atomic decomposition,finite martingale,density

O211.4

A

1008-5513(2009)03-0417-08

2007-05-08.

國家自然科學(xué)基金(10371093),湖北省高等學(xué)校自然科學(xué)研究計劃重點項目(D200613001).

于林(1965-),博士,教授,研究方向：鞅論及其在泛函分析與調(diào)和分析中的應(yīng)用.

2000MSC:60G42,60G48,46E30