Scalar or Vector Tetraquark State Candidate: Zc(4100)?
Zhi-Gang Wang (王志剛)
Department of Physics, North China Electric Power University, Baoding 071003, China
Abstract In this article, we separate the vector and axialvector components of the tensor diquark operators explicitly,construct the axialvector-axialvector type and vector-vector type scalar tetraquark currents and scalar-tensor type tensor tetraquark current to study the scalar, vector and axialvector tetraquark states with the QCD sum rules in a consistent way.The present calculations do not favor assigning the Zc(4100) to be a scalar or vector tetraquark state.If the Zc(4100) is a scalar tetraquark state without mixing effects, it should have a mass about 3.9 GeV or 4.0 GeV rather than 4.1 GeV; on the other hand, if the Zc(4100) is a vector tetraquark state, it should have a mass about 4.2 GeV rather than 4.1 GeV.However, if we introduce mixing, a mixing scalar tetraquark state can have a mass about 4.1 GeV.As a byproduct, we obtain an axialvector tetraquark candidate for the Zc(4020).
Key words:Tetraquark state, QCD sum rules
1 Introduction
The attractive interactions of one-gluon exchange favor formation of the diquarks in color antitriplet.[1]The diquarks (or diquark operators)εabcqTb CΓq′cin color antitriplet have five structures in Dirac spinor space, whereCΓ=C,Cγ5,Cγμγ5,CγμandCσμνfor the pseudoscalar(P),scalar(S),vector(V),axialvector(A)and tensor(T)diquarks, respectively, thea,b,care color indexes.The pseudoscalar,scalar,vector and axialvector diquarks have been studied with the QCD sum rules in details, which indicate that the favored configurations are the scalar and axialvector diquark states.[2?4]The scalar and axialvector diquark operators have been applied extensively to construct the tetraquark currents to study the lowest tetraquark states.[5?12]
In 2018, the LHCb Collaboration performed a Dalitz plot analysis ofB0→ ηcK+π?decays and observed an evidence for an exoticηcπ?resonant state.[13]The significance of this exotic resonance is more than three standard deviations, the measured mass and width are 4096±20MeV and 152±58MeV,respectively.The spin-parity assignmentsJP=0+and 1?are both consistent with the experimental data.[13]Is it a candidate for a scalar tetraquark state,[12,14,15]hadrocharmonium,[16]D?molecular state,[17]or charge conjugation of theZ+c(4050)?[18]
In Refs.[9]and [10], we study theandscalar tetraquark states with the QCD sum rules systematically, and obtain the ground state massesMSS=3.89±0.05 GeVMAA=MPP=5.48±0.10 GeV andMVV=for theSS,AA,PPandV Vdiquark-antidiquark type tetraquark states, respectively.The larger uncertaintiesGeV andGeV(compared to the uncertainties±0.05 GeV,±0.10 GeV andGeV) in the ground state masses originate from the QCD sum rules,where both the ground state and the first radial excited state are taken into account at the hadron side.If only the ground states are taken into account in the QCD sum rules, the uncertainties|δM|≤0.10 GeV, so the uncertaintiesGeV andGeV (±0.10 GeV) can be referred to as ”larger uncertainties” (”smaller uncertainties”).
In Ref.[11], we tentatively assign theX?(3860) to be the-type scalar tetraquark state, study its mass and width with the QCD sum rules in details, and obtain the massMSS=3.86±0.09 GeV.Now we can see that the SU(3) breaking effects of the masses of theandtetraquark states from the QCD sum rules are rather small, roughly speaking, they have degenerate masses.If we take the larger uncertainty, the predicted massMAA=3.92GeV for thetetraquark state has overlap with the experimental dataMZc=4096±20MeV marginally,[13]and favors assigning theZc(4100) to be theAA-type scalar tetraquark state.[14]On the other hand, if we take the smaller uncertainty, the predicted massMAA=3.92±0.10 GeV for thetetraquark state has no overlap with the experimental dataMZc=4096±20MeV, and disfavors assigning theZc(4100) to be theAA-type scalar tetraquark state.In a word, it is not robust assigning theZc(4100)to be theAA-type scalar tetraquark state.
In Ref.[12], Sundu, Agaev and Azizi obtain the massMSS=4.08±0.15 GeV, which differs from the predictionMSS=3.86±0.09 GeV greatly.[11]The differences originate from the different input parameters at the QCD side and different pole contributions at the hadron side.In Ref.[11],the pole contribution is about(46?70)%,which is much larger than the pole contribution in Ref.[12].While in early works, we took the pole contributions>50% and chose the energy scales of the QCD spectral densities to beμ=1 GeV, and obtained almost degenerate massesMSS ≈MAA ≈4.4 GeV,[6]which are much larger than the valueMSS=4.08±0.15 GeV.[12]In Ref.[8],we observe that the energy scaleμ=1 GeV is not the optimal energy scale for the hidden-charm tetraquark states.
In summary, the QCD sum rules do not favor assigning theZc(4100)to be the[qc]S[]S-type,[qc]A[]A-type,[qc]P[]P-type and [qc]V[]V-type scalar tetraquark states.
In Refs.[14, 19], we take the scalar and axialvector diquark operators as basic constituents, introduce an explicit P-wave between the diquark and antidiquark operators to construct the vector tetraquark currents,and study the vector tetraquark states with the QCD sum rules systematically, and obtain the lowest vector tetraquark masses up to now,MY=4.24±0.10 GeV,4.28±0.10 GeV, 4.31±0.10 GeV and 4.33±0.10 GeV for the tetraquark statesandrespectively, where the tetraquark states are defined bytheS,LandJare the diquark spin,angular momentum and total angular momentum,respectively.For other QCD sum rules with the [qc]S?μ[]Stype interpolating currents, one can consult Ref.[20].In fact, if we take the pseudoscalar and vector diquark operators as the basic constituents, even (or much) larger tetraquark masses are obtained.[21?23]Up to now, it is obvious that the QCD sum rules do not favor assigning theZc(4100) to be the vector tetraquark state.
It is interesting to analyze the properties of the tensor diquark states, and take the tensor diquark operators as the basic constituents to construct the tetraquark currents to study theZc(4100).
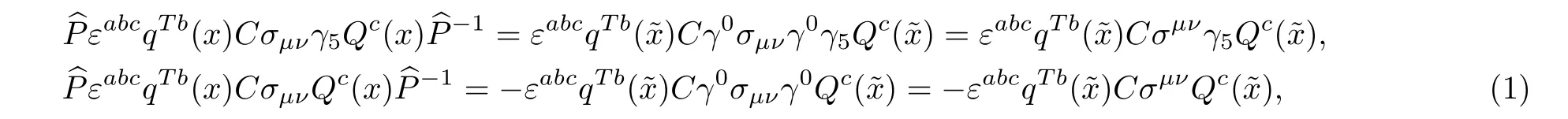
where the four vectorsxμ=() andand we have used the properties of the Diracγ-matrixes,The tensor diquark states have bothJP=1+and 1?components,
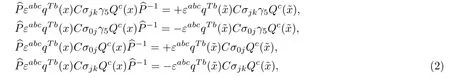
wherej,k=1, 2, 3, and we have used the properties of the Diracγ-matrixes,γ0=γ0,γj=?γj,σjk=σjkandσ0j=?σ0j.Now we introduce the four vectortμ=(1) and project out the 1+and 1?components explicitly,
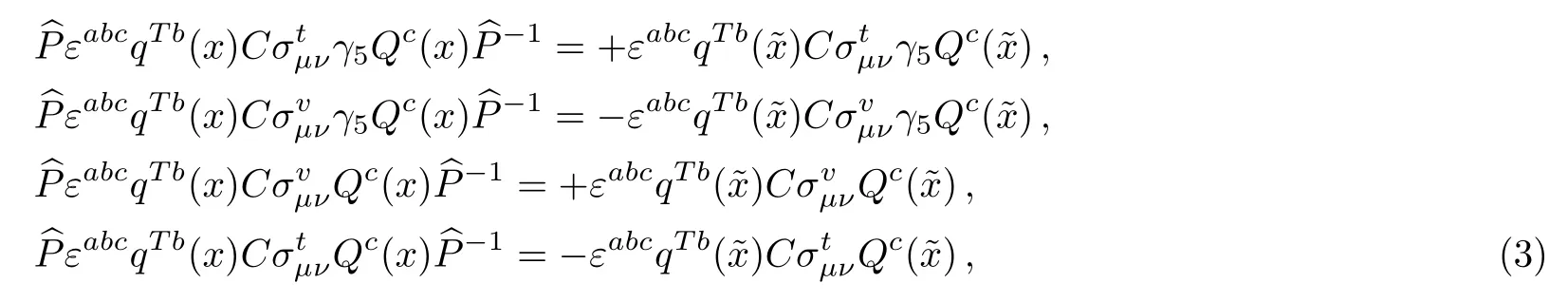
where
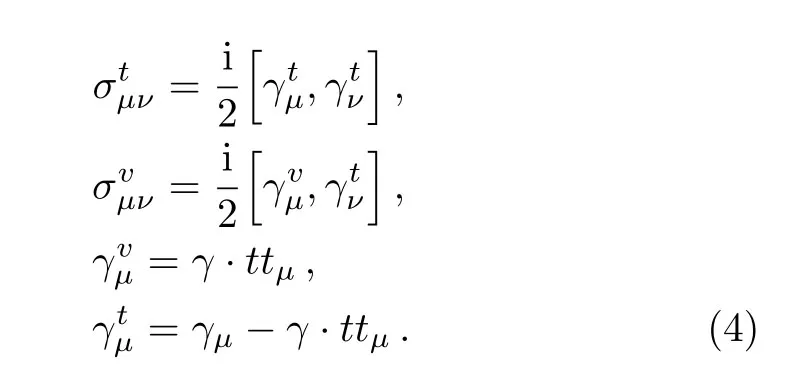
In this article, we choose the axialvector diquark operatorand vector diquark operatorto construct the tetraquark operators.On the other hand, if we choose the axialvector diquark operatorand vector diquark operatorto construct the tetraquark operators,we can obtain the same predictions.
In this article, we separate the vector () and axialvector () components of the tensor diquark operators explicitly,construct the-type and-type scalar tetraquark currents, and theST-type tensor tetraquark current to study theZc(4100) with the QCD sum rules,and try to assign theZc(4100) in the scenario of scalar and vector tetraquark states once more.
The article is arranged as follows:we derive the QCD sum rules for the masses and pole residues of the tetraquark states in Sec.2; in Sec.3, we present the numerical results and discussions; Sec.4 is reserved for our conclusion.
2 QCD Sum Rules for the Scalar and Vector Tetraquark States
Firstly, we write down the two-point correlation functions in the QCD sum rules,

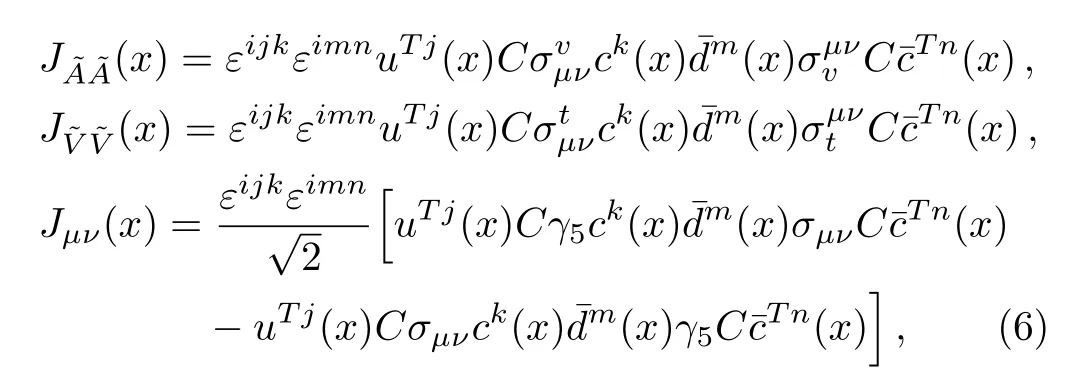
thei,j,k,m,nare color indexes.We take the isospin limit by assuming theuanddquarks have degenerate masses.Under charge conjugation transform, the currentsJ(x) andJμν(x) have the properties,
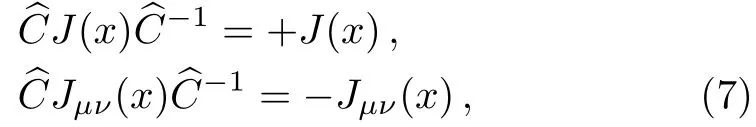
the currents have definite charge conjugation.The currentsJ(x) couple potentially to the scalar tetraquark states, while the currentJμν(x) couples potentially to both theJPC=1+?and 1??tetraquark states,
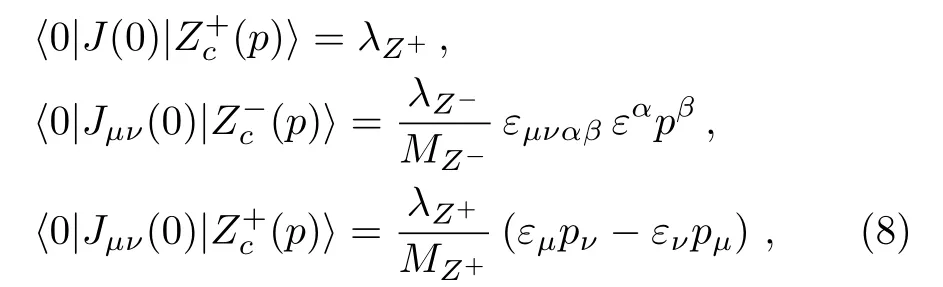
theεμ/αare the polarization vectors of the tetraquark states, the superscripts±denote the positive parity and negative parity, respectively, theMZ±andλZ±are the masses and pole residues, respectively.
We insert a complete set of intermediate hadronic states with the same quantum numbers as the current operators into the correlation functions to obtain the hadronic representation,[24,25]and isolate the ground state tetraquark contributions,
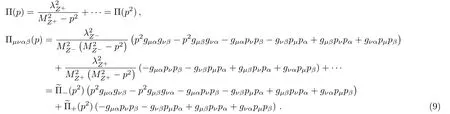
We can project out the components Π±(p2) explicitly by introducing the operators,
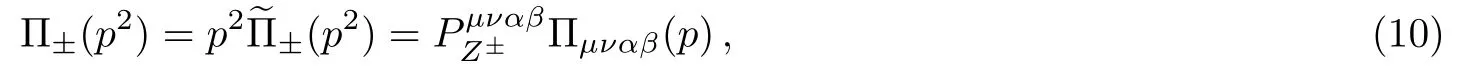
where
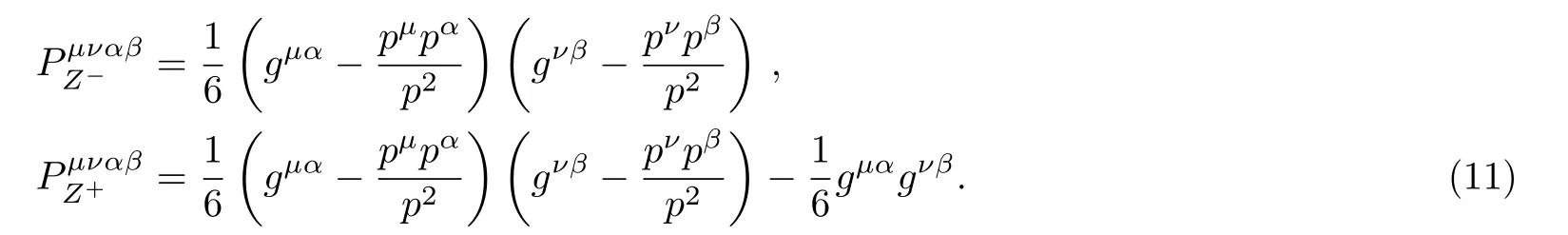
In this article, we choose the correlation functions Π(p2), Π?(p2) and Π+(p2) to study the scalar, vector and axialvector tetraquark states, respectively.
If we cannot project out the components Π±(p2) explicitly, we have to choose the currents(x) and(x),
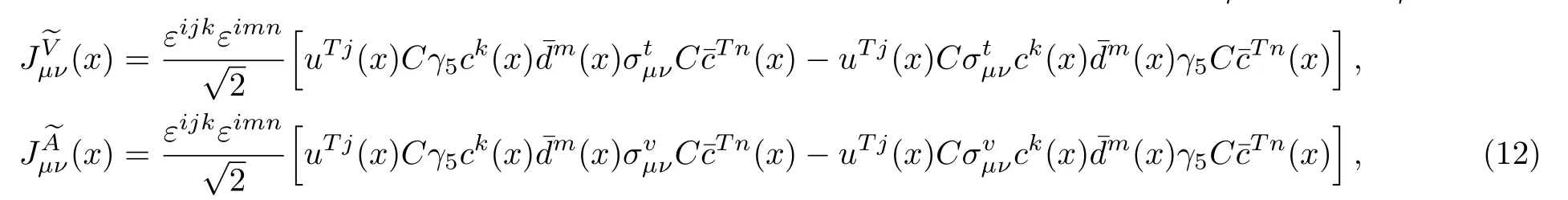
which couple to theJP=1?and 1+tetraquark states respectively,
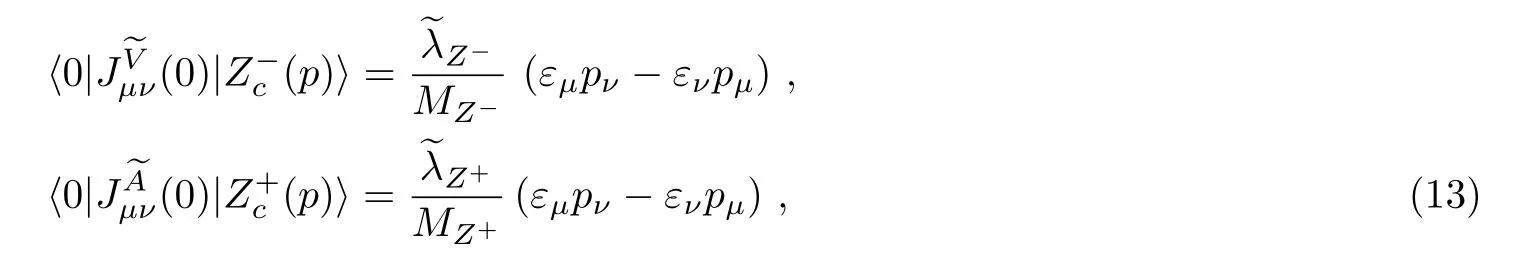
as the current operators(x)and(x)have the properties,
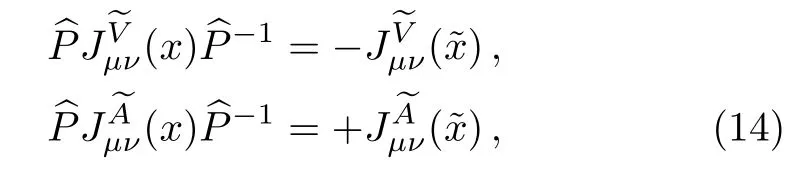
It is more easy to carry out the operator product expansion for the currentJμν(x) than for the currents(x) and(x).In this article, we prefer the currentJμν(x),and denote the corresponding vector and axialvector tetraquark states astype andtype, respectively.
We carry out the operator product expansion for the correlation functions up to the vacuum condensates of dimension 10 in a consistent way,then obtain the QCD spectral densities through dispersion relation, take the quarkhadron duality below the continuum thresholds0and perform Borel transform with respect toP2=?p2to obtain the QCD sum rules:
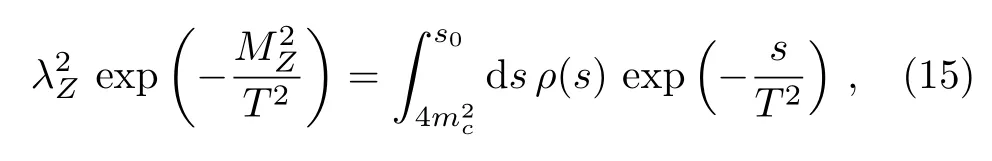
theρ(s) are the QCD spectral densities.The explicit expressions of the QCD spectral densities are available upon request by contacting me with E-mail.For the technical details, one can consult Refs.[8, 23].In carrying out the operator product expansion for the correlation functions Π(p), we encounter the terms (p·t)2, and set (p·t)2=p2,just like in the QCD sum rules for the baryon states separating the contributions of the positive parity and negative parity, where we take the four vectorpμ=(p0).[26]
We derive Eq.(15)with respect toτ=,and obtain the QCD sum rules for the masses of the scalar, vector and axialvector tetraquark statesZcthrough a ratio,
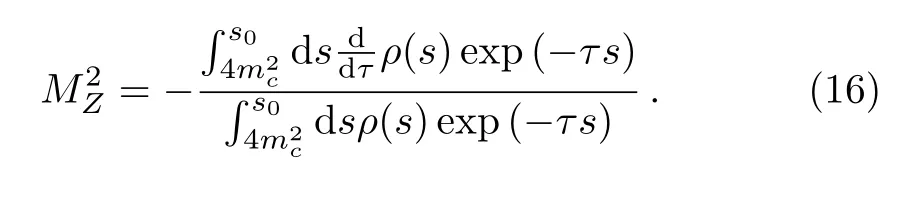
3 Numerical Results and Discussions
We choose the standard values of the vacuum condensatesat the energy scaleμ=1 GeV,[24,25,27]and choose themassmc(mc)=(1.275±0.025)GeV from the Particle Data Group,[28]and setmu=md=0.Moreover, we take into account the energy-scale dependence of the input parameters at the QCD side,
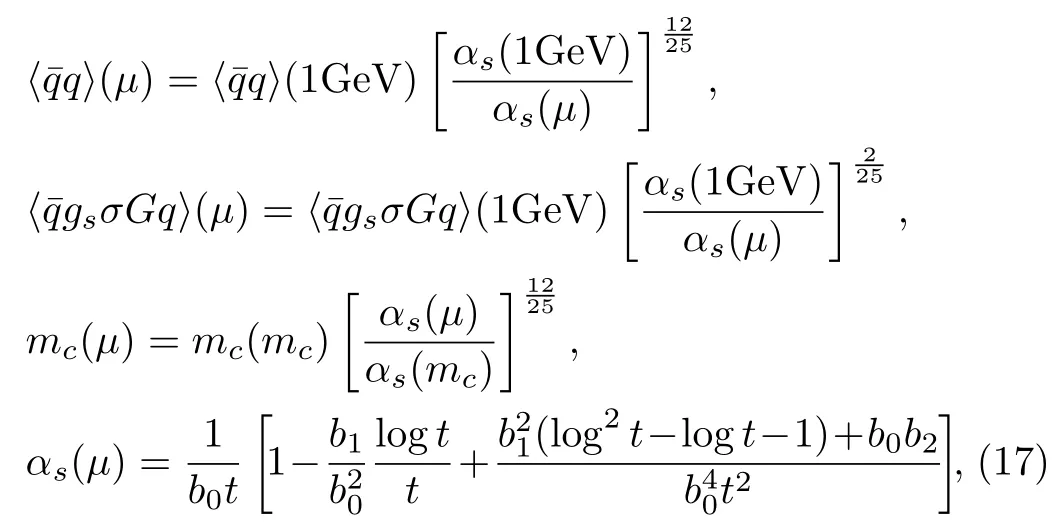
where
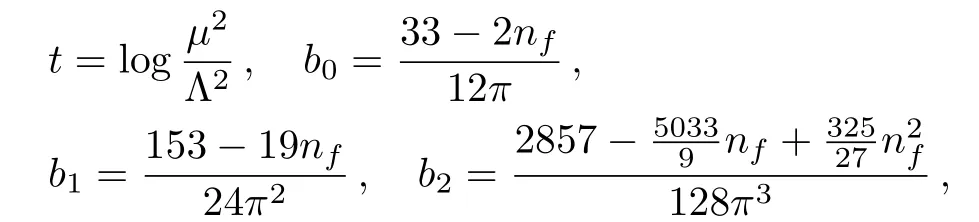
Λ=210 MeV, 292 MeV and 332 MeV for the flavorsnf=5, 4 and 3, respectively,[28,29]and evolve all the input parameters to the ideal energy scalesμto extract the tetraquark masses.In the present work,we choose the flavornf=4.
Now we search for the ideal Borel parametersT2and continuum threshold parameterss0to satisfy the four criteria:
(a) Pole dominance at the hadron side;
(b) Convergence of the operator product expansion;
(c) Appearance of the Borel platforms;
(d) Satisfying the energy scale formula,
via try and error.The resulting Borel parameters, continuum threshold parameters, energy scales of the QCD spectral densities and pole contributions are shown explicitly in Table 1.From the Table, we can see that the pole contributions are about (40?60)%, the pole dominance condition at the hadron side is well satisfied.In calculations, we observe that the contributions of the vacuum condensates of dimension 10 are?1%, the operator product expansion is well convergent.
We take into account the uncertainties of the input parameters and obtain the masses and pole residues of the tetraquark states, which are shown explicitly in Table 2 and in Figs.1 and 2.From Tables 1 and 2,we can see that the energy scale formulais well satisfied, where we take the updated value of the effectivec-quark mass Mc=1.82 GeV.[22]In Figs.1 and 2, we plot the masses and pole residues of the tetraquark states with variations of the Borel parameters at much larger ranges than the Borel widows, the regions between the two perpendicular lines are the Borel windows.In the Borel windows, the uncertainties induced by the Borel parameters are?1% for the masses and≤2% for the pole residues,there appear Borel platforms.Now the four criteria are all satisfied, we expect to make reliable predictions.
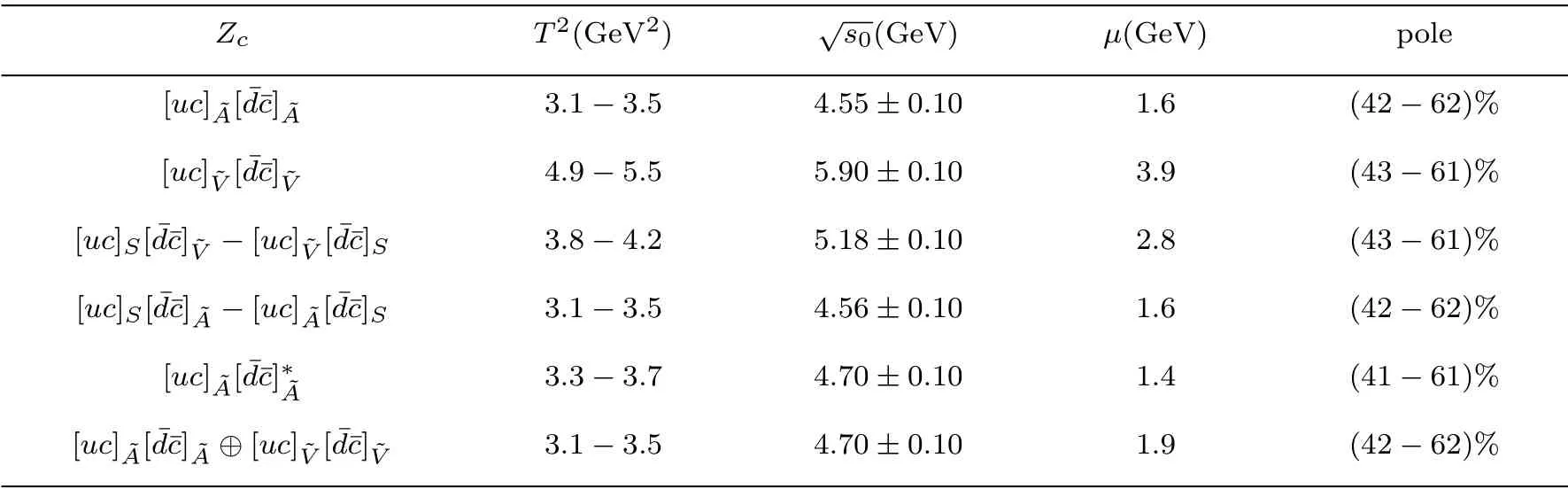
Table 1 The Borel parameters, continuum threshold parameters, energy scales of the QCD spectral densities and pole contributions of the ground state tetraquark states, where the superscript ?denotes the energy scale formula is not satisfied.
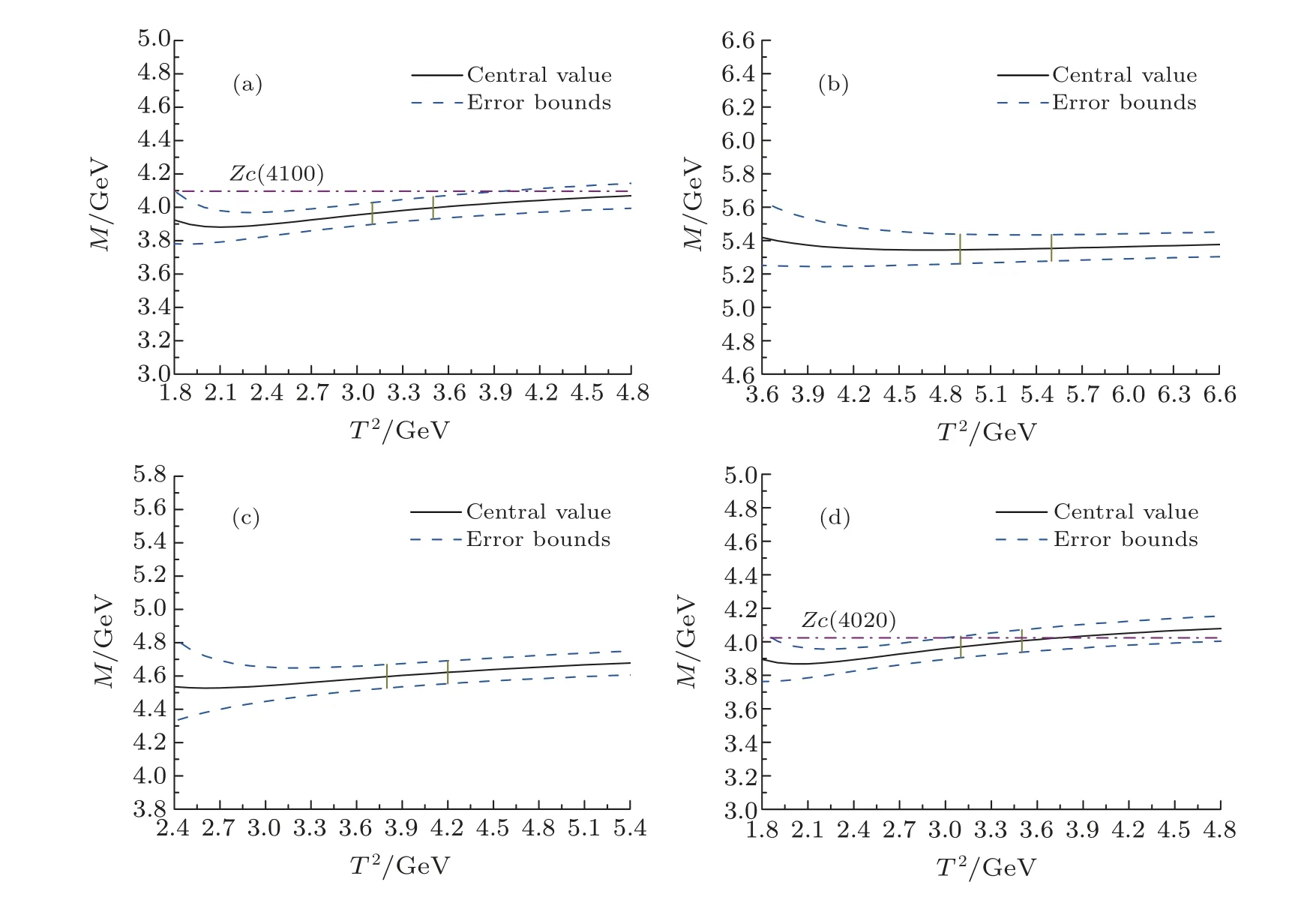
Fig.1 The masses with variations of the Borel parameters T2 for the tetraquark states, (a), (b), (c) and (d) denote the and tetraquark states, respectively, the regions between the two perpendicular lines are the Borel windows.

Table 2 The masses and pole residues of the ground state tetraquark states, where the superscript ?denotes the energy scale formula is not satisfied.
In Ref.[30], we study the tensor-tensor type scalar hidden-charm tetraquark states with currents
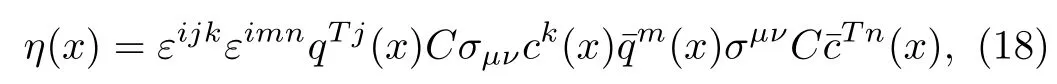
via the QCD sum rules by taking into account both the ground state contributions and the first radial excited state contributions, whereσvμν, and obtain massesMTT,1S=3.82±0.16 GeV andMTT,2S=4.38±0.09 GeV.We can rewrite the currentη(x) as a linear superpositionη(x)=(x)+(x),the tensor-tensor type scalar hidden-charm tetraquark states have both theandcomponents.Compared to the() type tetraquark mass=3.98±0.08 GeV(=5.35±0.09 GeV),the ground state massMTT,1S=3.82±0.16 GeV is (much) lower.In the QCD sum rules for the tensor-tensor type scalar tetraquark states, the termsmcandmcdisappear due to the special superpositionη(x)=(x)+(x),the contamination from thecomponent is large.
In Fig.1, we also present the experimental values of the masses of theZc(4100) andZc(4020).[13,28,31,32]From the figure, we can see that the predicted mass for thetype axialvector tetraquark state is in excellent agreement with the experimental data in the Borel window, and favors assigning theZc(4020) to be the type axialvector tetraquarkstate, while theZc(4100) lies above the-type scalar tetraquark state, and much below the-type scalar tetraquark state and-type vector tetraquark state in the Borel windows, the present QCD sum rules do not favor assigning theZc(4100) to be the scalar or vector tetraquark state.The masses of the scalar hidden-charm tetraquark states have the hierarchy,[9,10,11]
the QCD sum rules disfavor assigning theZc(4100) to be a scalar tetraquark state.
The masses extracted from the QCD sum rules depend on the Borel windows,different Borel windows lead to different predicted masses.From Fig.1(a),we can see that if we choose larger Borel parameter for the-type scalar tetraquark state, for example, chooseT2>4.2 GeV2rather than chooseT2=(3.1?3.5)GeV2,we can obtain a mass about 4.1 GeV, which is compatible with the experimental value of the mass of theZc(4100).If we choose the Borel windowT2=(4.9?5.3)GeV2, the predicted mass=4.09±0.08 GeV, which is in excellent agreement with the experimental dataMZc=4096±MeV.[13]However, the pole contribution is about (14?24)%, the prediction is not robust.
The massextracted from the QCD sum rules decreases monotonously with increase of the energy scales of the QCD spectral density.If we chooseμ=1.4 GeV,T2=(3.3?3.7)GeV2,=4.70±0.10 GeV, the pole contribution is (41?61)% and the operator product expansion is well convergent,we obtain the tetraquark mass=4.12±0.08 GeV, which is in excellent agreement with the experimental dataMZc=4096±MeV,[13]see Fig.3.In Fig.3, we plot the massextracted at the energy scaleμ=1.4 GeV with variation of the Borel parameter, again the region between the two perpendicular lines is the Borel windows.However, the energy scale formulais not satisfied.In the QCD sum rules for the hidden-charm (or hidden-bottom)tetraquark states and molecular states, the integrals
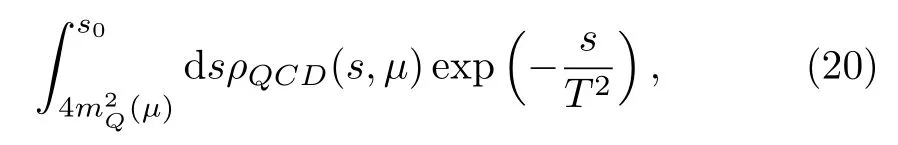
are sensitive to the energy scalesμ.We suggest an energy scale formulawith the effectiveQ-quark mass MQto determine the ideal energy scales of the QCD spectral densities in a consistent way.[23]
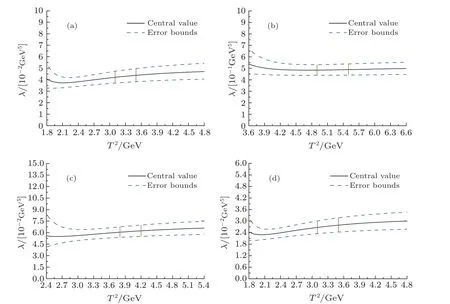
Fig.2 The pole residues with variations of the Borel parameters T2 for the tetraquark states, (a), (b), (c) and (d) denote the and tetraquark states, respectively, the regions between the two perpendicular lines are the Borel windows.
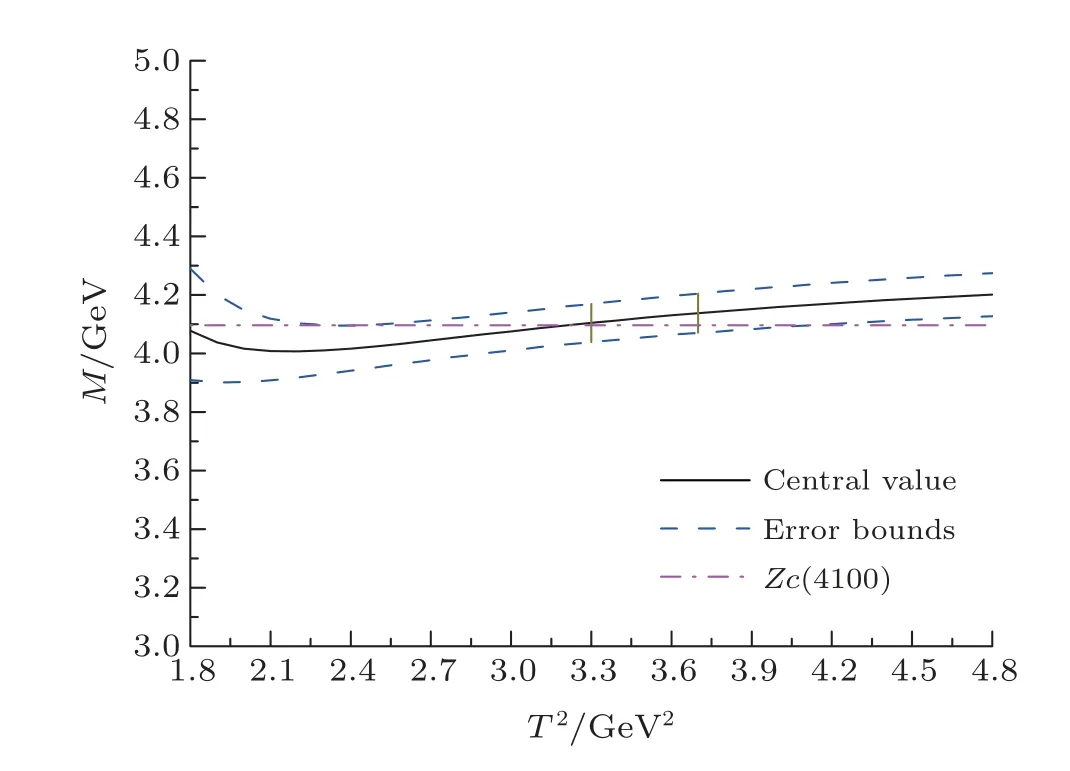
Fig.3 The mass with variation of the Borel parameter T2 for the type scalar tetraquark state at the energy scale μ=1.4 GeV, the region between the two perpendicular line is the Borel window.
The energy scale formula works well for the tetraquark states,[8?11,22,23,33,34]tetraquark molecular states,[35]and even for the hidden-charm pentaquark states.[36]For example, in Refs.[8,22,33]and the present work, we observe that there exist one axialvector tetraquark candidatefor theZc(3900), three axialvector tetraquark candidatesandfor theZc(4020),which is consistent with the almost degenerate scalar and axialvector heavy diquark masses from the QCD sum rules [3].Furthermore, theZc(4430) can be assigned to be the first radial excited state of theZc(3900).If theZc(4100) is a diquark-antidiquark type scalar tetraquark state, the energy scale formula should be satisfied,as theZc(4100)has no reason to be an odd or special tetraquark state.The masses of the scalar tetraquark statesSS,AAandare estimated to be 3.9?4.0 GeV,if the spin-spin interactions are neglected,the QCD sum rules support this estimation.
In Ref.[12], Sundu, Agaev and Azizi choose theSStype scalar current to study the mass and width of theZc(4100), and obtain the massMSS=4.08±0.15 GeV with the pole contribution (19?54)%.In Ref.[11],we tentatively assign theX?(3860) to be the [qc]S[]Stype scalar tetraquark state, study its mass and width with the QCD sum rules, and obtain the massMSS=3.86±0.09 GeV with the pole contribution (46?70)%,which is much larger than the pole contribution(19?54)%in Ref.[12].In Ref.[11], just like in the present work, we use the energy scale formulato enhance the pole contribution.In the QCD sum rules,we prefer larger pole contributions to obtain more robust predictions.
Now we assume that theZc(4100) is a⊕type mixing scalar tetraquark state, and study it with the currentJ(x),
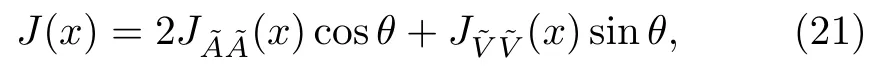
where we introduce the factor 2 due to the relationσμν=+.If we choose the mixing angleθ=26.4?, the energy scaleμ=1.9 GeV, the Borel parameterT2=(3.1?3.5)GeV2, the continuum threshold parameter=4.70±0.10 GeV, the pole contribution is(42?62)%, the operator product expansion is well convergent, the energy scale formula is also satisfied.We obtain the tetraquark mass=4.10±0.09 GeV,which is in excellent agreement with the experimental dataMZc=4096±MeV,[13]see Fig.4.If theZc(4100)is a diquark-antidiquark type tetraquark state, it may be a⊕type mixing scalar tetraquark state.
We can also introduce more parameters and write down the most general scalar currentJ(x),
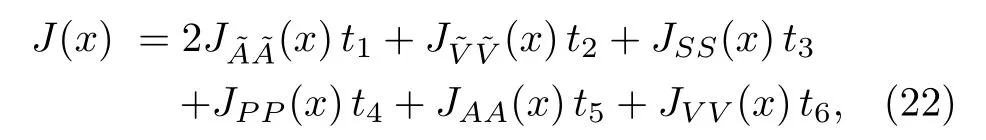
where
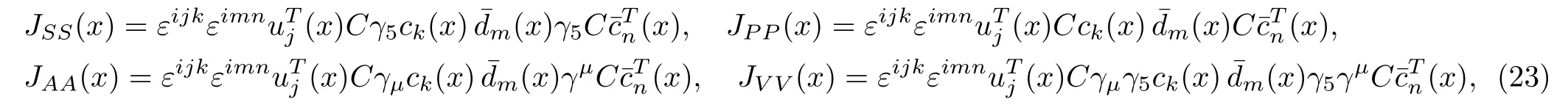
thetiwithi=1, 2, 3,···are arbitrary parameters.We can obtain any value between the largest massMPPand the smallest massMSSby fine tuning the parametersti, see Eq.(19).In fact, we cannot assign a tetraquark state unambiguously with the mass alone, we have to study the decays exclusively to obtain the partial decay widths and confront the predictions to experimental data in the future.The cumbersome calculations may be our next work.In the present work, we can obtain the conclusion tentatively that we cannot reproduce the experimental value of the mass ofZc(4100) without introducing mixing effects.
In this article, we take the zero width approximation.In fact, we can take into account the finite width effect with the simple replacement of the hadronic spectral density,
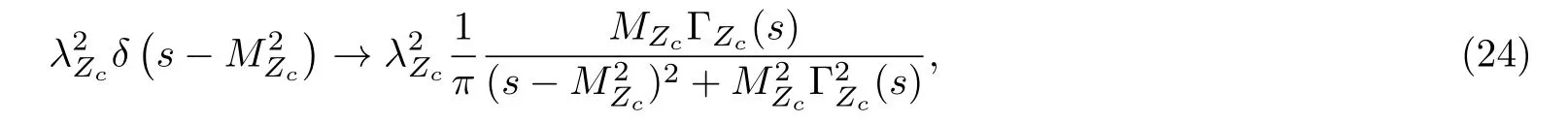
where
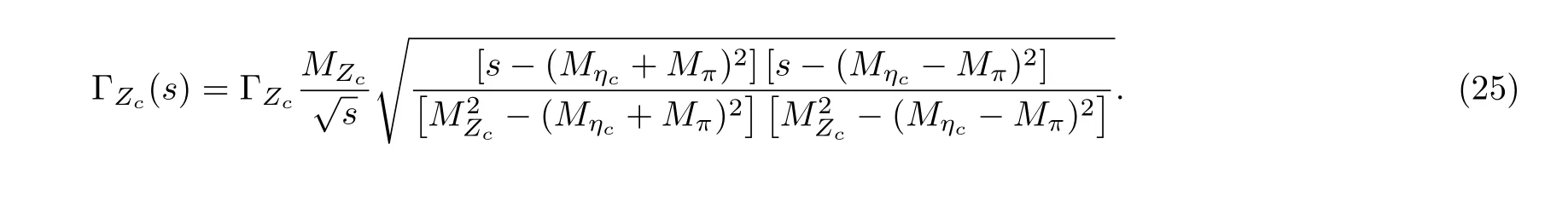
Then the hadron sides of the QCD sum rules in Eqs.(15)–(16) undergo the changes,
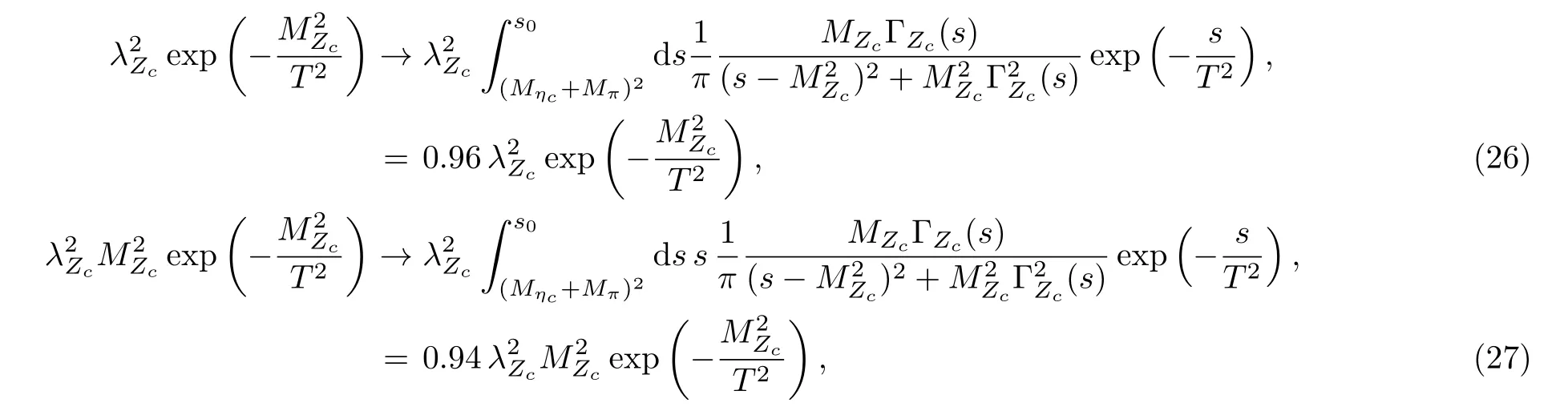
where we have used the central values of the input parameters for thetype scalar tetraquark state shown in Table 1 and the physical values of the mass and width of theZc(4100).We can absorb the numerical factors 0.96 and 0.94 into the pole residueλZcsafely with the simple replacementλZc →(0.97?0.98)λZc, the zero width approximation works well.
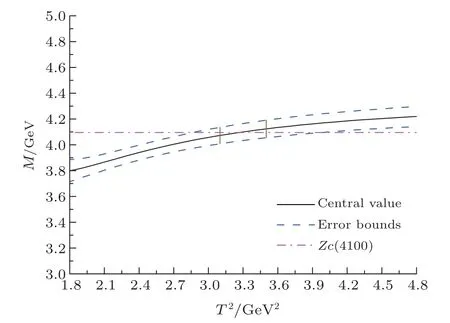
Fig.4 The mass with variation of the Borel parameter T2 for the ⊕type scalar tetraquark state, the region between the two perpendicular line is the Borel window.
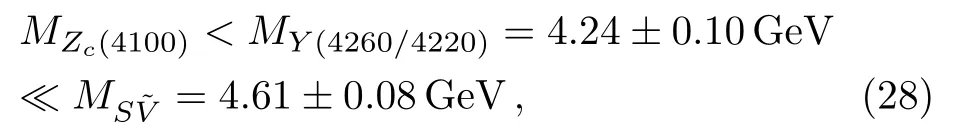
the QCD sum rules also disfavor assigning theZc(4100)to be a vector tetraquark state.
If theZc(4100) is aSS,AAortype scalar hidden-charm tetraquark state without mixing effects, it should have a mass about 3.9 GeV or 4.0 GeV rather than 4.1 GeV; on the other hand, if theZc(4100) is a vector hidden-charm tetraquark state, it should have a mass about 4.2 GeV rather than 4.1 GeV.However,a⊕type mixing scalar tetraquark state can have a mass about 4.1 GeV and reproduce the experimental value of the mass of theZc(4100).[13]
TheZ?c(4100)is observed in theηcπ?mass spectrum,the spin-parity assignmentsJP=0+and 1?are both consistent with the experimental data.We can search for its charge zero partnerZ0c(4100) in theηcπ0mass spectrum,if theηcπ0is in relative S-wave, theZ0c(4100) has theJPC=0++, on the other hand, if theηcπ0is in relative P-wave, theZ0c(4100) has theJPC=1?+.The quantum numbersJPC=1?+is exotic, we can also search for theZ0c(4100) in theJ/ψρ0mass spectrum, which maybe shed light on the nature of theZc(4100).In Ref.[23],we observe that the diquark-antidiquark type vector(or) tetraquark state withJPC=1?+has smaller mass than the corresponding vector tetraquark state withJPC=1??, about 0.09 GeV.In the present case, we can choose the currentημν(x),
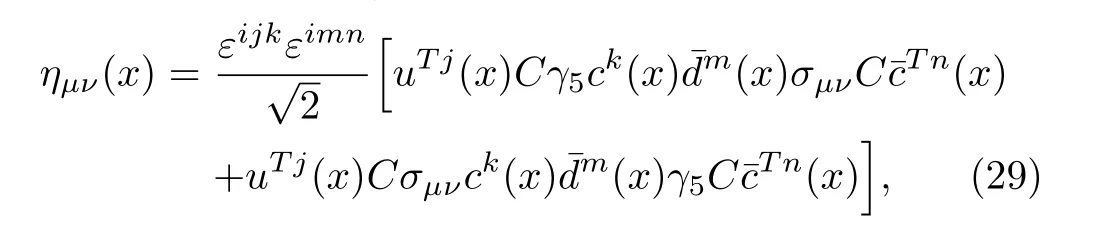
which couples potentially to the vector tetraquark state withJPC=1?+, the mass of the vector tetraquark state withJPC=1?+is estimated to be 4.52±0.08 GeV,which is much larger than the experimental value of the mass of theZ?c(4100), 4096±MeV.
4 Conclusion
In this article, we separate the vector and axialvector components of the tensor diquark operators explicitly,construct the axialvector-axialvector-type and vectorvector type scalar tetraquark currents and scalar-tensor type tensor tetraquark current to study the scalar, vector and axialvector tetraquark states with the QCD sum rules by carrying out the operator product expansion up to vacuum condensates of dimension 10 in a consistent way.In calculation, we use the energy scale formula to determine the ideal energy scales of the QCD spectral densities to extract the masses from the QCD sum rules with the pole contributions about (40?60)%.The present calculations do not favor assigning theZc(4100)to be the scalar or vector tetraquark state.If theZc(4100)is a scalar tetraquark state without mixing effects, it should have a mass about 3.9 GeV or 4.0 GeV rather than 4.1 GeV; on the other hand,if theZc(4100)is a vector tetraquark state,it should have a mass about 4.2 GeV rather than 4.1 GeV.If we introduce mixing effects, a⊕type mixing scalar tetraquark state can have a mass about 4.1 GeV.More precise measurements of the mass, width and quantum numbers are still needed.As a byproduct, we obtain an axialvector tetraquark candidate for theZc(4020).
 Communications in Theoretical Physics2019年11期
Communications in Theoretical Physics2019年11期
- Communications in Theoretical Physics的其它文章
- Structure, Electronic, and Mechanical Properties of Three Fully Hydrogenation h-BN:Theoretical Investigations?
- Polarized Debye Sheath in Degenerate Plasmas?
- Absorption Enhancement of Ultrathin Crystalline Silicon Solar Cells with Dielectric Si3N4 Nanostructures?
- Fractional Angular Momentum of an Atom on a Noncommutative Plane?
- Similar Early Growth of Out-of-time-ordered Correlators in Quantum Chaotic and Integrable Ising Chains?
- Neural-Network Quantum State of Transverse-Field Ising Model?
