張 超,張?jiān)屏?/p>

(1.河北北方學(xué)院理學(xué)院數(shù)學(xué)系,河北張家口075000;2.張家口市第一中學(xué),河北張家口075000)

在現(xiàn)實(shí)生活中,存在大量的最優(yōu)化問題,將它們抽象成優(yōu)化模型后,大都可以歸結(jié)為求全局解的問題,從而促使在最近二三十年里,全局最優(yōu)化以驚人的速度在許多領(lǐng)域取得了快速發(fā)展,許多新的理論及算法被廣泛的應(yīng)用于科學(xué)和工程中遇到的難題上,特別是最近出現(xiàn)的全局優(yōu)化方法[1]作為強(qiáng)有力的工具被成功的應(yīng)用于人們的生產(chǎn)和設(shè)計(jì)問題中.在解決最優(yōu)化問題的眾多方法中,填充函數(shù)法是比較有效的一種方法.本文將討論使用填充函數(shù)法求解帶一般約束的全局優(yōu)化問題[2].

1 構(gòu)造新填充函數(shù)

假設(shè) f(x)在 Rn上連續(xù)可微且滿足強(qiáng)制性條件(x) =+∞,并且存在一個(gè)有界閉區(qū)域Ω?Rn包含了f(x)所有的全局極小解,除此之外還假設(shè)局部極小解的個(gè)數(shù)為有限個(gè) (每個(gè)極小解都是孤立的).

本文就要求解的問題 (P)給出了以下三個(gè)假設(shè)條件:f(x)是連續(xù)的;f(x)有有限個(gè)局部極小值;S是連續(xù)區(qū)域.

在第二條假設(shè)中,盡管 f(x)有有限個(gè)局部極小值,但是卻有可能擁有無限個(gè)局部極小解[3].

定義1 假設(shè)x＊是f(x)的當(dāng)前局部極小解,L(x,,ε)被稱為f(x)在點(diǎn)處的填充函數(shù),如果它滿足以下的性質(zhì):

(1)x＊是L(x,,ε)的最大解,且f(x)的整個(gè)谷域?yàn)長(x,,ε)山域的一部分;

(3)如果f(x)在x＊存在一個(gè)比低的谷域B＊,那么在B＊中存在一個(gè)點(diǎn)x′使L(x,,ε)在和的連線上取得最小,是 x＊的某個(gè)領(lǐng)域中的任意一點(diǎn).)

注意到定義中的第三條與多年前葛仁浦首次提出的填充函數(shù)[4]的概念有所不同,與相連的不是一個(gè)點(diǎn)而是 x＊的某個(gè)領(lǐng)域的每個(gè)點(diǎn).

下面就是本文所構(gòu)造的填充函數(shù):

x＊是問題 f(x)的當(dāng)前局部極小解,ε是一個(gè)大于0小于1的正常數(shù).

考慮下面的一般約束化問題:

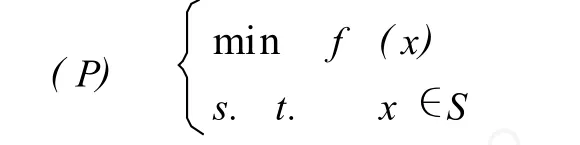
其中 f(x)是連線可微函數(shù),s={x∈Rn|gi(x)≥0,i=1,2,…,m;hi(x)=0,j=1,2,…,l},

2 填充函數(shù)的證明與相關(guān)定理

參數(shù)ε是一個(gè)屬于區(qū)間 (0,1)之間的數(shù).從以上的證明看出,在計(jì)算過程中ε是不用調(diào)整的,可以是一個(gè)預(yù)先給定的非常小的正數(shù).經(jīng)反復(fù)的實(shí)驗(yàn)發(fā)現(xiàn):當(dāng)逐漸變小時(shí),計(jì)算效果會(huì)越變?cè)胶?

3 算 法

根據(jù)前面的分析于證明,下面將給出一個(gè)實(shí)際的算法[8],來求解所構(gòu)造的新的填充函數(shù),以便得到優(yōu)于當(dāng)前最優(yōu)解得更好的解.具體算法描述如下:

Step1 隨機(jī)選取一點(diǎn)x∈X,從該點(diǎn)出發(fā)在S中最小化f(x)得到了問題(P)的一個(gè)最小解x1＊,令ε取一個(gè)非常小的正數(shù),另外選一個(gè)整數(shù)NL.

Step3 如果N≥NL,轉(zhuǎn)到Step6.

Step5 通過初始點(diǎn)x′在集合S中最小化f(x),并且得到了f(x)的一個(gè)局部最小解.令=然后就回到Step2.

Step6 停止計(jì)算,分別輸出問題(P)近似的全局最優(yōu)解和相應(yīng)的全局最優(yōu)值f().

[1] Zhang LS,Ng C,Li D,et al.A new filled f unction method for global optimization[J].Global Optim,2001,20：49-65

[2] 申培萍.全局優(yōu)化方法 [M].北京：科學(xué)出版社,2006：152-209

[3] Han QM,Han JY.Revised filled function methods for global optimization[J].Appl Math Comput,2001(119)：217-228

[4] Ge RP.A filled function method for finding a global minimizer of a f unction of several varables[J].Math Program,1990,46：191-204

[5] 姚亦榮,韓伯順,張連生.尋求全局最優(yōu)解的一個(gè)新的填充函數(shù) [J].上海大學(xué)學(xué)報(bào),2006,(09)：308-312

[6] Ge RP,Qin YF.A class of filled f unctions of finding global minimizers of a f unction of several variables[J].Optim Theory Appl,1987,52：240-252

[7] Ge RP,Qin YF.The golball convexized filled functions for global optimization[J].Appl Math Comput,1990,33：131-158

[8] Zhang LS,Wolfe MA.An interval algorithm for nondifferentiable global optimization[J].Appl Math Comput,1994,63：101-122

[9] Zhu WX.A class of filled functions irrelevant to the number of local mini-mizers of global optimization[J].System Math Sci,2002,22(04)：406-413