LIU Shi-he, YIN Shu-ran

College of Water Resource and Hydropower, Wuhan University, Wuhan 430072, China, E-mail: shihe3086@163.com

GUO Wei

Yangtze River Scientific Research Institute, Wuhan 430010, China

(Received November 9, 2009, Revised December 29 2009)

TURBULENT FLOWS AROUND SAND DUNES IN ALLUVIAL RIVERS*

LIU Shi-he, YIN Shu-ran

College of Water Resource and Hydropower, Wuhan University, Wuhan 430072, China, E-mail: shihe3086@163.com

GUO Wei

Yangtze River Scientific Research Institute, Wuhan 430010, China

(Received November 9, 2009, Revised December 29 2009)

The sand dunes are typical bed forms of natural alluvial rivers. In this article, a vertical 2-D Reynolds stress model is established for the simulation of turbulent flows around sand dunes, and water-sand boundary conditions are set with particular attention. By numerical simulations, the following conclusions can be drawn. (1) The flow resistance in rivers with sand dunes could be divided into the sand-grain resistance and the sand dune resistance, and the sand-grain resistance coefficient mainly depends on Reynolds number, relative sand grain roughness and sand dune steepness. This coefficient in rivers with sand dunes would be larger than that calculated in a flat riverbed, and the steeper the sand dunes, the larger the sand-grain resistance coefficient. (2) The sand dune resistance coefficient mainly depends on the relative sand dune height and sand dune steepness, the steeper the sand dunes, the larger the sand dune resistance coefficient. (3) For the flat riverbed, the turbulent eddy viscosity coefficient and the sediment diffusion coefficient are approximately identical, but for the sand dune riverbed, in the vertical position, where the sediment diffusion coefficient reaches its maximum, it would be higher than the turbulent eddy viscosity coefficient.

sand dune, flow resistance, sediment diffusion coefficient, eddy viscosity

1. Introduction

The sand dunes are typical bed forms of natural alluvial rivers. The study of flows around sand dunes in alluvial rivers is very important both in basic sciences and engineering applications, because it not only concerns the mechanism of flow resistance and sediment transport, but also can help to establish a better mathematical model to simulate sediment-laden flows for flood control, navigation, etc. Liu et al.[1]analyzed the river flow around sand waves and sandbars based on the rapid distortion theory. Bai et al.[2]conducted experimental research on turbulent characteristics of flows over sand ripples. Huo et al.[3]performed experimental research on the time variation of the bed shear stress under the wave effect. In the field of numerical simulations. Yoon and Patel[4]simulated turbulent flows over sand dunes by k-ω turbulence model. Yue[5]further simulated the turbulent flow over a fixed two-dimensional sand dune by large eddy simulation. On the other hand, the riverbed with sand dunes is also one kind of wavy boundaries, similar to the ocean surface with wind-waves[6], the corrugated tubes and sinusoidal wavy cylinder[7]in some industrial installations. There were numerous researches on turbulent flows around common wavy boundaries such as the sine wave boundary. For example, Zilker and Hanratty[8]used the hot film sensor to measure the velocity distribution, and adopted the electric-chemical method to make the actual measurement of the wall shear stress on the sine wave boundary. Hudson et al.[9]used LDV to measure velocity on the sine wave train. Markatos[10]used a standard k-ω model to simulate turbulent flowsover arbitrary shapes. Cherukat et al.[11]adopted the direct numerical simulation to study fully developed turbulent flows over a sine wave wall.

Generally speaking, the formation and evolution of sand dunes in natural alluvial rivers depend on both the bed material composition and flow characteristics. The calculation of sand-grain resistance in alluvial rivers with sand dunes is currently simplified to the calculation in a static flat bed (without sand dunes) due to the lack of appropriate information, which inevitably results in some errors. In addition, the sediment diffusion coefficient is generally approximated by the turbulent eddy viscosity coefficient of flows in the study of the vertical distribution of the suspended sediment concentration in river dynamics. However, there is not much study concerning the validity of this simplification for river flows with sand dunes. Furthermore, very few numerical simulations for flows around sand dunes consider water-sand boundary conditions, which would lead to inaccurate results to some extent due to the effect of sand grains on the characteristics of turbulent flows around sand dunes composed of sand grains.

In this article the vertical 2-D Reynolds stress model is employed for simulating turbulent flows around sand dunes, and particular attention is paid to the treatment of the water-sand boundary conditions in order to provide some insight on above issues.

2. Mathematical model and numerical method

2.1 Governing equations

The governing equations for the vertical 2-D Reynolds stress model are as follows:

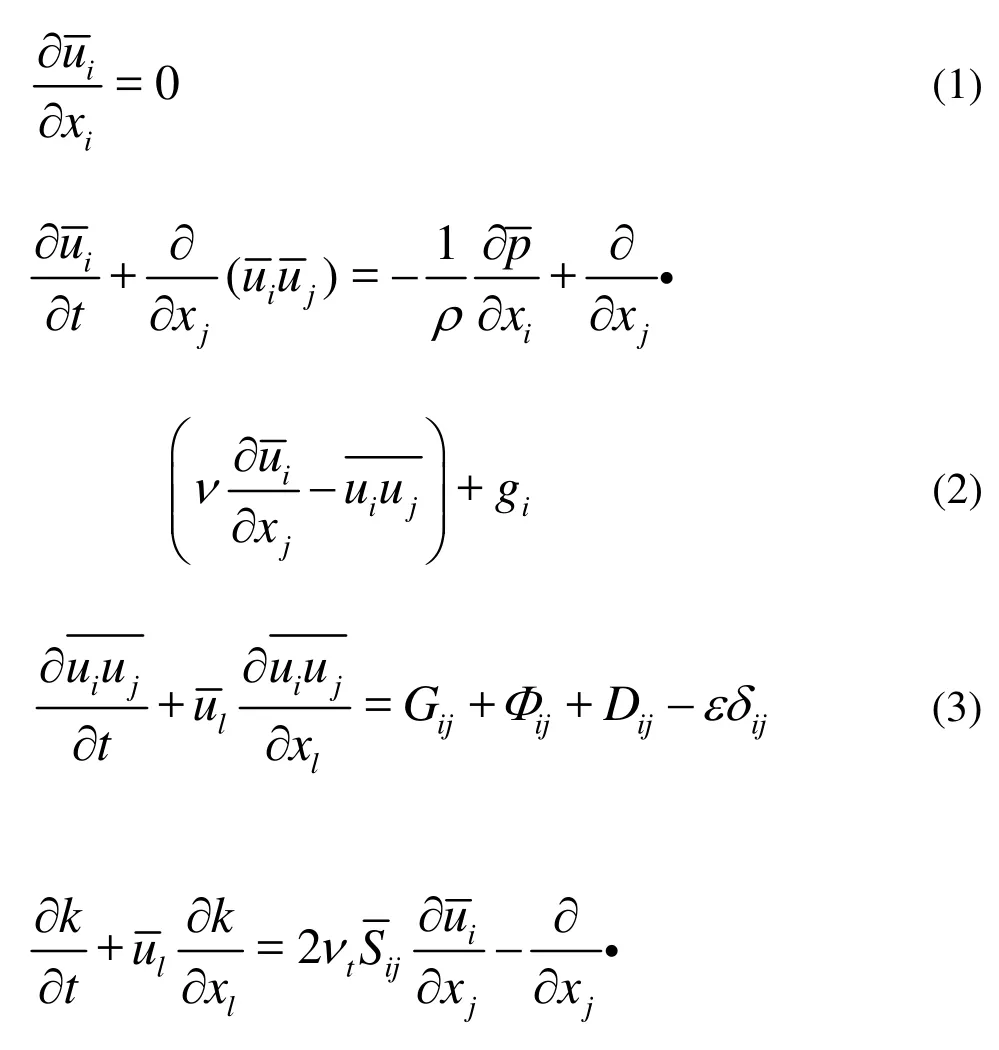
Equations (1) and (2) are Reynolds equations, whereandrefer to the mean velocity and the mean pressure, respectively, ν and νtare the kinematical viscosity coefficient and the turbulent eddy viscosity coefficient, respectively, ρ andare the density of water and Reynolds stress tensor, respectively. Equation (3) is Reynolds stress equation, where Gij,Φijand Dijare Reynolds stress generation term, the pressure dependent variable and the diffusion term, respectively, and are calculated based on models in relation to the turbulent kinetic energy, the turbulent kinetic energy dissipation rate, and others. Equations (4) and (5) are the turbulent kinetic energy equation and the turbulent kinetic energy dissipation rate equation, respectively, whereijrefers to the strain-rate tensor of the mean velocity field, k andε refer to the turbulent kinetic energy and the turbulent kinetic dissipation rate, respectively, σk, σε, Cε1and Cε2are empirical parameters. For details about the calculation of the above terms and the determination of the empirical parameters, see Ref.[12].

2.2 Boundary conditions

2.2.1 Water-sand boundary

The formation of sand dunes is related to the bed material composition and the turbulent flow characteristics. In Fig.1 a sketch of sand dunes in alluvial rivers is given. Due to the coupling effect it is almost impossible to describe the geometric characteristics of sand dunes by only one parameter. In this article, the sand dune steepness Δ/λ, the relative sand dune height Δ/Rb(Rb=H is the hydraulic radius) and the relative sand grain roughness d50/Rb(d50is the median diameter of the bed material) are adopted to describe the coupling effect between the bed material composition and the turbulent flow characteristics. According to Ref.[13], Δ/λ usually ranges between 0.05-0.2.

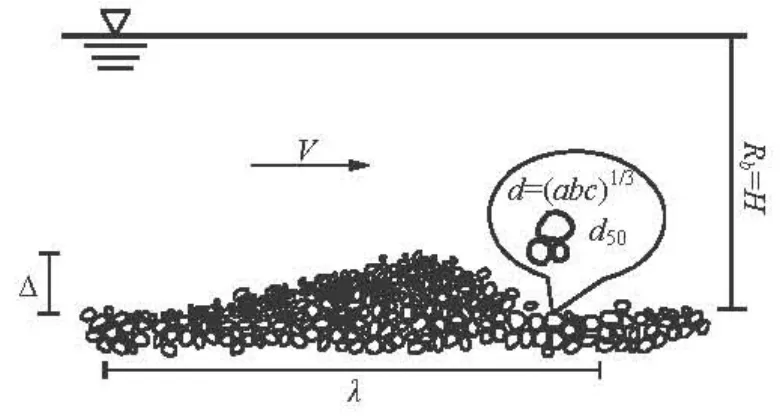
Fig.1 Sketch of sand dune on riverbed

The sand dune is composed of sand grains, thus both the scales of the sand dune and the sand grain will influence the turbulent flow. Based on the studies in Ref.[13,14], the zero position of the bed is taken as 0.75d50, and the longitudinal velocityPis calculated by the formula suggested in Ref.[14], which satisfies all wall conditions, including the hydraulic smooth region, transitional region and rough region.

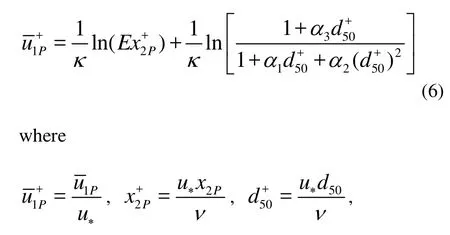
u?is the shear velocity, x2Pis the vertical distance away from the surface of the sand dunes and k=0.4, E=9.8, α1=0.0175, α2=0.002, α3=0.019.

2.2.2 Water-air boundary

The water-air boundary condition is determined according to the rigid-lid hypothesis, because, generally speaking, the effect of sand dunes on the turbulent flow can only be observed within several sand dune heights and the ratio of water depth to sand dune height adopted in this article is large enough.

2.3 Numerical scheme

In the numerical simulation, the fitting quadrilateral meshes of 1530×50 are used. For sand dune riverbeds with different d50, the distance between the first layer of meshes and the surface of the sand dune is approximately 0.5 mm-3.5 mm.

The governing equations are discretised by FVM over the control volume, a third-order accuracy QUICK scheme is used for the convection term while the central difference scheme is used for the diffusion term. The variables are evaluated at the center of the control volume and the arrangement of collocated variables is employed to deal with the coupling relationship between pressure and velocity.

The algebraic equations are solved by the Gauss-Seidel iteration method. The converging criterion is that the unit mass flow residue should be less than 0.01% of the inflow and the overall mass flow residue should be less than 0.5% of the inflow.

3. Validation

3.1 Mean velocity

In Ref.[13], the longitudinal mean velocity in different vertical positions around sand dunes was measured a comparison between the measured mean velocity and the calculated values by this article is given in Fig.2. As can be seen from this figure, the calculated and measured velocities are in good agreement.

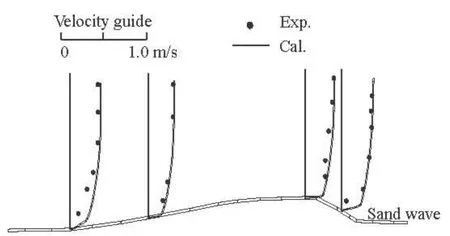
Fig.2 Comparison of the measured and calculated longitudinal mean velocities around sand dunes

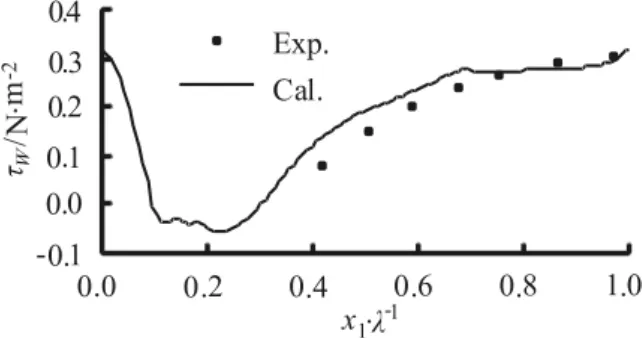
Fig.3 Comparison of the measured and calculated wall shear stresses on sand dunes

3.2 Wall shear stress

In Ref.[13], the wall shear stress on sand dunes was measured. A comparison between the measured wall shear stress and the calculated values by this article is given in Fig.3. As can be seen from this figure, the calculated and measured wall shear stresses are also in good agreement.

The riverbed with sand dunes is in a kind of wavy boundaries and for various forms of wavy boundaries such as the sine wave boundary, Zilker and Hanratty[8]measured the wall shear stress by the electric-chemical method. A comparison between the measured wall shear stress and the calculated values by this article is given in Fig.4, which shows a good agreement.

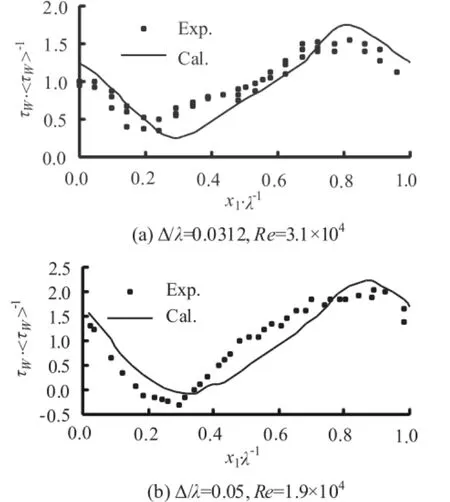
Fig.4 Wall shear stress distribution on sine wavy boundary, wτ refers to the wavy shear stress, ＜wτ＞ refers to the average shear stress within a wavelength, λ refers to the wave length of wavy boundary

4. Discussion on flow resistance in alluvial rivers with sand dunes

As mentioned above, the sand dune is composed of sand grains and hence the flow resistance could be further divided into the sand-grain resistance and the sand dune resistance. It is of significance to distinguish these resistances in alluvial rivers to better understand the total resistance and the sediment movement[13].

4.1 Sand-grain resistance

Sand-grain resistance FSis a surface resistance, which can be obtained by the integration of the wall shear stress τx1on the surface of sand dunes within a wavelength, i.e.,

The mean sand-grain resistance coefficient FSfor a single sand dune is defined as

where V refers to the mean velocity in the section. Previous studies show thatfSmainly depends on Reynolds number Re=VRb/ν, relative sand grain roughness d50/Rband sand dune steepness Δ/λ[16].

In Fig.5 the measured variations of fSwithRe and d50/Rband those calculated in this article are compared, in whichΔ/λ and d50keep as constants with Δ/λ=0.15 and d50=1.75mm As can be seen from this figure,fSslightly decreases with the increase of Re, yet increases with the increase of d50/Rb.

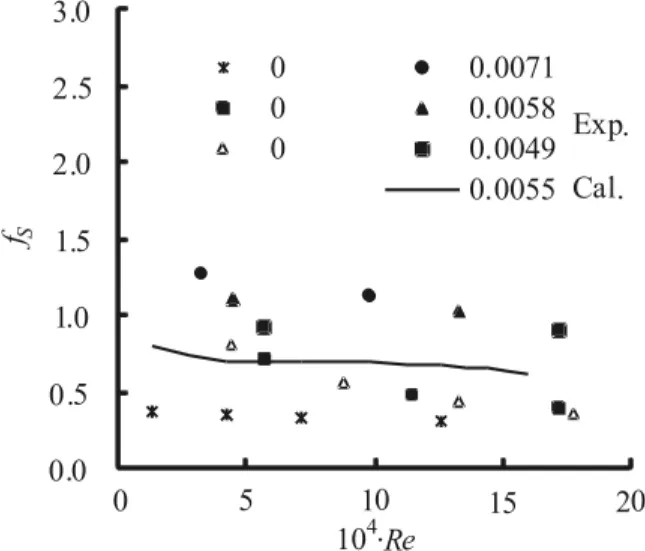
Fig.5 Variations of fSwith Re and d50/Rb, with experimental results from Ref. [16]

In Fig.6, the measured variations of fSwith Refor the sand dune riverbed (Δ/λ≠0) and the flat riverbed (Δ/λ=0) are compared with the calculated ones in this article, in which d50/Rbkeeps as constant (=0.0061). As can be seen from this figure that: (1)fSrapidly decreases with the increase of Reuntil Re is larger than a certain value,fSthen keeps unchanged with the increase of Re, (2)fSin rivers with sand dunes is larger than that calculated in the flat riverbed, and the larger the sand dune steepness Δ/λ, the larger the sand-grain resistance coefficient fS.

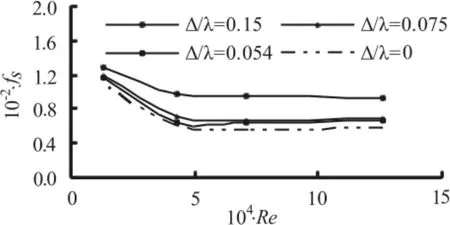
Fig.6 Variations of fSwith Re and Δ/λ

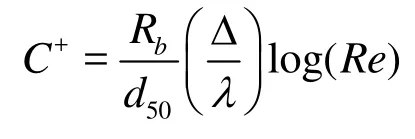
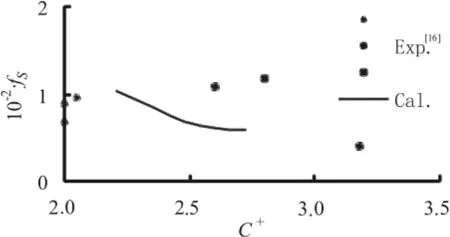
Fig.7 Variation of fSwith C+, with experimental results from Ref.[16]

4.2 Sand dune resistance

Sand dune resistance FDresults from the asymmetric pressure distribution on sand dunes, which can be obtained by the integration of pressure pwithin a wavelength, i.e.,

where θ refers to the angle between the sand dune surface and the horizontal plane. Similar to Eq.(9) the mean sand dune resistance coefficient fDfor a single sand dune is defined as

The sand dune resistance coefficient strongly depends on the sand dune shape. In Ref.[16], based on the analysis of experimental results, the following formula for fDwas proposed:

It was indicated that the parameter m in Eq.(12) is related toΔ/λ, but no detailed relation was given, except that a value of 4/9 was recommended. In Fig.8, the calculated results of this article are given, together with Eq.(12). As can be seen from this figure, the two results are in good agreement. In Fig.9, our calculated results for the variation of m withΔ/λ are given. As can be seen from this figure, the larger the sand dune steepness Δ/λ, the larger the coefficient m.

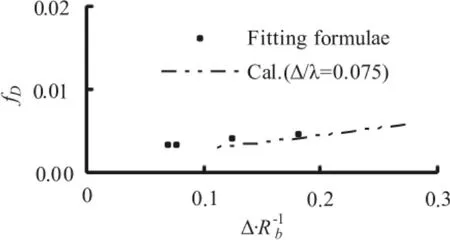
Fig.8 The variation of fDwith Δ/Rb

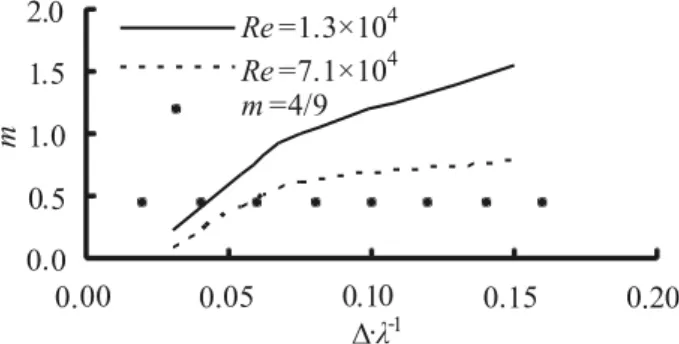
Fig.9 The variation of m withΔ/λ

4.3 Comparison of sand-grain resistance and sand dune resistance

The flow separation in the leeward of sand dunes results in changes of wall shear stress and pressure imposed on the surface of sand dunes, since the extent of the flow separation is related to Δ/λ. The sand-grain resistance and the sand dune resistance would also have the same tendency. In Fig.10, the variations of fSand fDwith Δ/λare given (while Re and d50/Rbkeep unchanged). As can be seen from Fig.10, (1)fSslightly increases with the increase of Δ/λ, while fDsharply increases with the increase of Δ/λ, (2) when Δ/λ is smaller thana certain value (0.07 in Fig.10), fDis less than fS, the sand-grain resistance dominates the flow resistance, but when Δ/λ is large enough, fDwould be much larger than fS, i.e., the flow resistance would be dominated by the sand dune resistance.

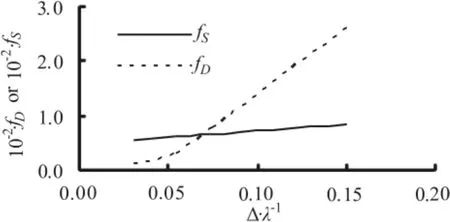
Fig.10 Comparison of sand-grain resistance coefficient and sand dune resistance coefficient

5. Discussion on turbulent eddy viscosity coefficient and sediment diffusion coefficient

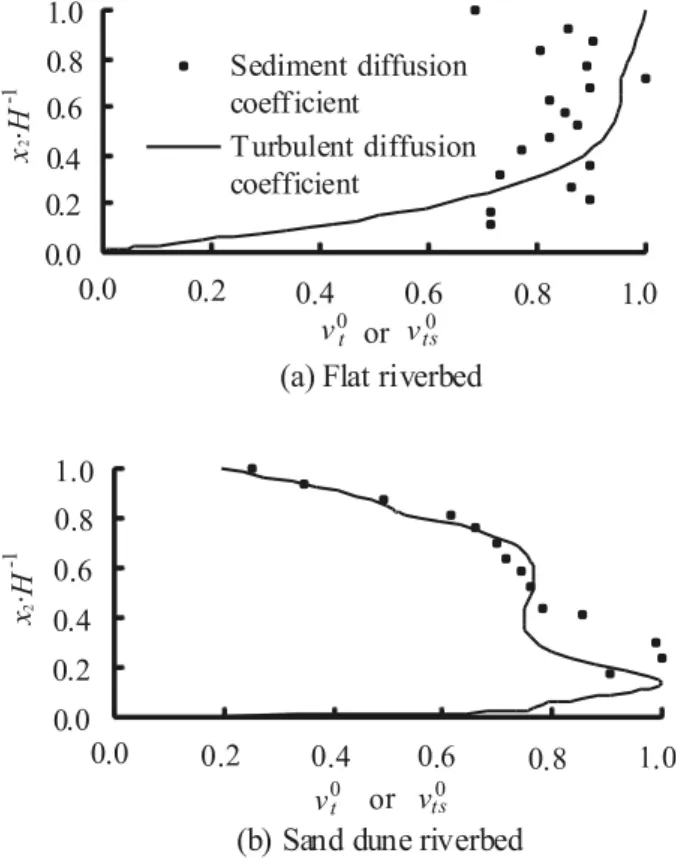
Fig.11 Vertical distributions of turbulent eddy viscosity coefficient and sediment diffusion coefficient

6. Conclusions

Based on the study of turbulent flows around sand dunes in alluvial rivers, the following conclusions are drawn:

(1) A vertical 2-D Reynolds stress model is established for the simulation of turbulent flows around sand dunes. The calculated mean velocity and wall shear stress by the present model are in good agreement with experimental results.

(2) The flow resistance in rivers with sand dunes could be divided into the sand-grain resistance and the sand dune resistance. The sand-grain resistance coefficient mainly depends on Reynolds number, relative sand grain roughness and sand dune steepness, and this coefficient in rivers with sand dunes would be larger than that calculated in a flat riverbed. The sand dune resistance coefficient mainly depends on the relative sand dune height and sand dune steepness. Furthermore, the steeper the sand dunes, the larger the sand-grain and sand dune resistance coefficients are.

(3) For the flat riverbed, the turbulent eddy viscosity coefficient and the sediment diffusion coefficient are approximately identical, but for the sand dune riverbed, in the vertical position, the sediment diffusion coefficient reaches its maximum, which would be higher than the related turbulent eddy viscosity coefficient.

References

[1] LIU Shi-he, XIONG Xiao-yuan and LUO Qiu-shi. Theoretical analysis and numerical simulation of turbulence flow around sand waves and sand bars[J]. Journal of Hydrodynamics, 2009, 21(2): 292-298.

[2] BAI Yu-chuan, XU Dong. Experimental study on turbulent characteristics of flow over sand ripples bed[J]. Journal of Hydrodynamics, Ser. B, 2006, 18(3): 449-454.

[3] HUO Guang, WANG Yi-gang. A new measure for direct measurement of the bed shear stress of wavy boundary layer in wave flume[J]. Journal of Hydrodynamics, Ser. B, 2007, 19(4): 517-524.

[4] YOON J. Y., PATEL V. C. Numerical model of turbulent flow over sand dune[J]. Journal of Hydraulic Engineering, 1996, 122(1): 10-18.

[5] YUE Wu-si, LIN Ching-long and PATEL C. V. Largeeddy simulation of turbulent flow over a fixed two-dimensional dune[J]. Journal of Hydraulic Engineering, 2006, 132(7): 643-651.

[6] ZHOU Liang-ming, WANG Ai-fang and GUO Pei-fang. Numerical simulation of sea surface directional wave spectra under typhoon wind forcing[J]. Journal of Hydrodynamics, 2008, 20(6): 776-783.

[7] ZOU Lin, LIN Yu-feng. Force reduction of flow around a sinusoidal wavy cylinder[J]. Journal of Hydrodynamics, 2009, 21(3): 308-315.

[8] ZILKER D. P., HANRATTY T. J. Influence of the amplitude of a solid wavy wall on a turbulent flow. Part 1 Separated flows[J]. Journal Fluid Mechanics, 1977, 82: 29-51.

[9] HUDSON J. D., DYKHNO L. and HANRATY T. J. Turbulence production in flow over a wavy wall[J]. Experiments in Fluids, 1996, 20(4): 257-265.

[10] MARKATOS N. C. G., SPALDING D. B. and TATCHELL D. G. et al. solution method for three-dimensional turbulent boundary layers on bodies of arbitrary shapes[J]. Computer Methods in Applied Mechanics and Engineering, 1978, 15: 74-161.

[11] CHERUKA P., NA Y. and HANRATTY T. J. et al. Direct numerical Simulation of a fully developed turbulent flow over a wavy wall[J]. Theoretical and Computational Fluid Dynamics, 1998, 11(2): 109-134.

[12] LIU Shi-he. High velocity flow[M]. Beijing: Science Press, 2005, 7-13(in Chinese).

[13] QIAN Ning, WAN Zhao-hui. Mechanics of sediment transport[M]. Beijing: Science Press, 2001, 145-189(in Chinese).

[14] LIU Shi-he, HUANG Wei and LUO Qiu-shi. Numerical simulation of compound open channel flow[J]. Engineering Journal of Wuhan University, 2006, 39(6): 1-5(in Chinese).

[15] TAO Wen-quan. Numerical heat transfer[M]. Xi’an: Xi’an Jiaotong University Press, 2001, 347-374(in Chinese).

[16] SHEH H. W., FEHLMAN H. M. and MENDOZA C. Bed form resistances in open channel flows[J]. Journal of Hydraulic Engineering, 1990, 116(6): 799-815.

[17] FENG Jing-ting, JIAO En-ze. River sediment hazard and prevention[M]. Bejing: China Water Power Press,1987, 44-47(in Chinese.).

10.1016/S1001-6058(09)60034-2

* Project support by the National Natural Science Foundation of China (Grant No. 50539060).

Biography: LIU Shi-he (1962-), Male, Ph. D., Professor