鮑文竹, 張兆迎

(成都信息工程學(xué)院數(shù)學(xué)學(xué)院,四川成都610225)

1 引言和主要結(jié)果

設(shè)F為復(fù)平面一區(qū)域D上的一族亞純函數(shù).如果F中任取一函數(shù)序列{fn(z)}均可選出一個(gè)子列{fnk(z)}在區(qū)域D上按球距內(nèi)閉一致收斂于一亞純函數(shù)或者∞,則稱F在區(qū)域D上正規(guī).

設(shè)f和g為定義在區(qū)域D上的兩個(gè)亞純函數(shù),a為一復(fù)數(shù),若 f(z)-a和g(z)-a有相同的零點(diǎn),則稱f(z)與g(z)在區(qū)域D內(nèi)分擔(dān)a,或稱IM分擔(dān)a.

把亞純函數(shù)正規(guī)族與分擔(dān)值結(jié)合起來(lái)考慮是亞純函數(shù)族理論研究的一個(gè)重要課題,這方面的工作由W.Schwick[1]開(kāi)始研究.近年來(lái)涉及導(dǎo)數(shù)的正規(guī)族理論取得了不少成果.Y.Wang和M.Fang于1998年證明了：

定理A[2]設(shè)f為復(fù)平面上的超越亞純函數(shù),k,n≥k+1為正整數(shù),則(fn)(k)取任何非零有限復(fù)數(shù)無(wú)窮多次.

W.Schick證明了與定理A相關(guān)的正規(guī)定則.

定理B[3]設(shè)F為區(qū)域D上的亞純函數(shù)族,k,n≥k+1為正整數(shù),若對(duì)任意 f∈F有(fn)(k)≠1,則F在區(qū)域D上正規(guī).

應(yīng)用Zalcman引理,容易證明定理B中的條件n≥k+3改為n≥k+1時(shí)結(jié)論也是成立的.最近Yuntong Li和Yongxing Gu又進(jìn)一步推廣了W.Schick的結(jié)論.

定理C[4]設(shè)F為區(qū)域D上的一族亞純函數(shù),,k,n≥k+2為正整數(shù),a≠0為有窮復(fù)數(shù),對(duì)任意的f,g∈F,(fn)(k)和(gn)(k)分擔(dān)a,則F在區(qū)域 D上正規(guī).

由于(fn)(k)與(gn)(k)是L(fn)與 L(gn)的特殊情形,很自然地考慮L(fn)與 L(gn)分擔(dān)a時(shí)F正規(guī)性的問(wèn)題,其中 L(fn)=a0(fn)(k)+a1(fn)(k-1)+,…,+ak(fn),a0≠0,a1,…,ak為復(fù)數(shù).

我們推廣了定理C得到了下述結(jié)果.

定理1 設(shè)F為區(qū)域D上的一族亞純函數(shù),k,n≥k+2為正整數(shù),a≠0為有窮復(fù)數(shù),對(duì)任意的 f,g∈F,L(fn),L(gn)在D上IM分擔(dān)a,則F在區(qū)域D上正規(guī).

在文獻(xiàn)[4]中已經(jīng)給出a≠0以及n≥k+2這兩個(gè)條件必要性的例子.

2 主要引理

對(duì)于研究正規(guī)族問(wèn)題,通常用的是Zalcman引理

引理1[5,6]設(shè)D為復(fù)平面上一個(gè)區(qū)域,F為區(qū)域D上的一個(gè)亞純函數(shù)族,-1＜α＜1.若F在D上不正規(guī),則存在

(1)點(diǎn)列 zn∈D,|zn|＜r＜1;

(2)函數(shù)列 fn∈F;

(3)正數(shù)列 ρn→0+,

引理2 設(shè)f為非常數(shù)亞純函數(shù),k,n≥k+2為正整數(shù),a≠0為有窮復(fù)數(shù),則(fn)(k)-a至少有兩個(gè)不同的零點(diǎn).

當(dāng)f為超越亞純函數(shù)時(shí),引理2為定理A;當(dāng) f為非常數(shù)有理函數(shù)時(shí),引理2文獻(xiàn)為[4]中引理2.

3 定理1的證明

假設(shè)F在內(nèi)D內(nèi)不正規(guī),則F至少在一點(diǎn)z0處不正規(guī).不失一般性,設(shè)z0=0,D為單位圓盤Δ.由引理1,存在

(1)點(diǎn)列 zn∈D,|zn|＜r＜1;

(2)函數(shù)列 fj∈F;

(3)正數(shù)列 ρj→0+,

從上式有

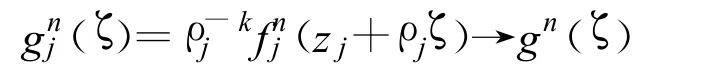
在復(fù)平面的除去g(ζ)的極點(diǎn)的緊集上一致成立故

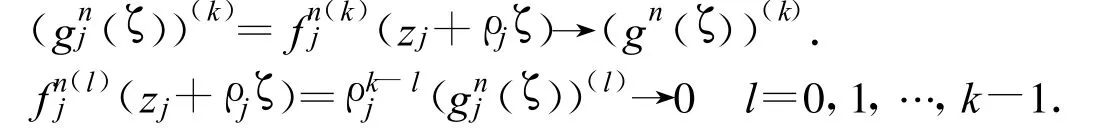
從而

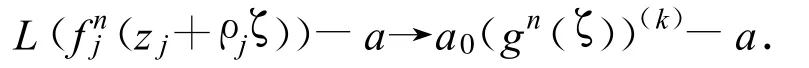
不妨設(shè) ζ0和 ζ0*為的兩個(gè)不同的零點(diǎn),選取 δ(＞0)使得.這里

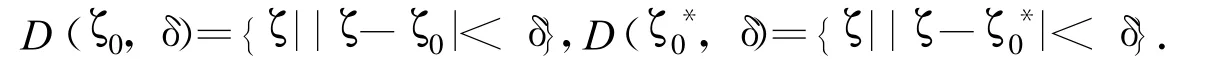
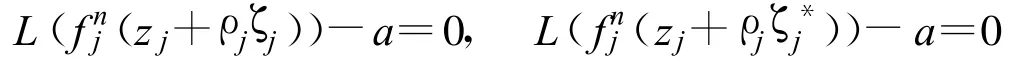
故對(duì)任意l∈N有

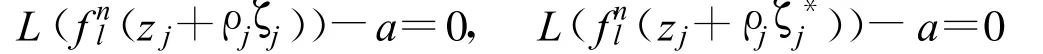
由非常數(shù)亞純函數(shù)零點(diǎn)的孤立性

故

定理1證畢.

[1]W Schwick.Sharing values and normality[J].Arch Math.,1992,59：50-54.

[2]Y F Wang,M L Fang.Picard values and normal families of meromorphic functions with multiple zeros[J].Acta Math.Sinica(in Chinese),1998,41：743-748.

[3]W Schwick.Normality criteria for families of meromorphic function[J].J.Anal.Math.,1989,52：241-289.

[4]Y F Li,Y X Gu.On normal familes of meromorphic function[J].J.Math.Anal.Appl.,2009,354：421-425.

[5]L Zalcman.Normal families：New perspectives[J].Bull.Amer.Math.Soc.,1998,35 ：215-230.

[6]X C Pang.Normality conditions for differential polynomials[J].Kexue Tongbao,1988,33：1690-1693.