黃永峰

(昌吉學(xué)院數(shù)學(xué)系,新疆昌吉 831100)

由上式知,

0 引 言

近年來,高階邊值問題因其在物理及工程學(xué)中較高的應(yīng)用價值而受到廣泛的關(guān)注.一些學(xué)者研究了高階邊值問題正解的存在性,得到了一些較好的結(jié)果[1,2].在研究中,學(xué)者們利用錐拉伸或錐壓縮定理以及不動點指數(shù)理論在非線性項滿足超線性或次線性條件獲得結(jié)論.此外,還有學(xué)者利用臨界點理論及Morse理論研究了高階邊值問題解的存在性[3-6].特別地,文獻(xiàn)[4]利用臨界點理論和Morse理論并結(jié)合局部環(huán)繞定理得到了四階帶參數(shù)Dirichlet邊值問題解的存在性,文獻(xiàn)[6]運用鞍點定理及臨界點理論得到了四階帶參數(shù)的Neumann邊值問題的解的存在性.基于以上的研究工作,本文考慮如下的問題,

1 預(yù)備知識

令 E=C[0,1]為[0,1]上的連續(xù)函數(shù)并按范數(shù) ‖u‖C=tm∈[a0x,1]|u(t)|構(gòu)成的實Banach空間, L2[0,1]為[0,1]上所有平方可積的函數(shù)構(gòu)成的實Hilbert空間,其范數(shù)為,

設(shè) Gi(t,s)為線性邊值問題,

由此知,邊值問題在 C4[0,1]中的解等價于下列方程,

在 C[0,1]中的解.

易知,G(t,s)為連續(xù)的,且邊值問題的解等價于積分方程,

令,

在 C[0,1]中的解.

定義算子 K,

則邊值問題在C4[0,1]中的解當(dāng)且僅當(dāng)其為算子方程,u=Kf→u,在 C[0,1]中的解.

為了證明需要,下面給出一些臨界點理論及局部環(huán)繞的基本定義和引理.

定義1[7]設(shè)D是實Banach空間E中的開集,泛函J:D→R1在D上是Frechet可微,若有,u0∈D,使得J′(u0)=0,則稱,u0是泛函J的一個臨界點.

定義2[7]設(shè) E實Banach空間,J∈C1(E, R1).如果,{un}? E,J(un)→c,J′(un)→θ,n→∞,蘊涵{un}有收斂子列,則稱泛函J滿足(PS)c條件.如果對于所有的c均滿足(PS)c條件,則稱泛函J滿足PS條件.

定義3[8]設(shè)J(θ)=0,E=V⊕X,dimV＜+∞,X為實Banach空間.如果存在ρ＞0,使得,

那么稱J在θ點局部環(huán)繞.

定義4[8]設(shè) u0是泛函J的一個孤立臨界點, J(u0)=c,U是u0的一個鄰域,且在U中,J除u0外沒有其他臨界點,稱,

Cq(J,u0)=Hq(Jc∩U,(Jc∩U){u0}),q=0,1,2,…,為J在u0的第 q個臨界群,其中,Hq(X,Y)為第 q個奇異相對同調(diào)群,其系數(shù)為整數(shù)群.若至少有一個臨界群是非平凡的,則稱 u0是J的一個同調(diào)非平凡臨界點.

引理1[9]算子方程,u=Kf→u,在 C[0,1]中有解,當(dāng)且僅當(dāng),v=K1/2f→K1/2v,在L2[0,1]中有解.

引理2[3]如果泛函,

有一個臨界點,u∈L2[0,1],則邊值問題在 C4[0, 1]中有一個解.

引理3[8]假設(shè)J∈C1(E,R1)滿足 PS條件,且在θ點局部環(huán)繞,則θ為J的一個同調(diào)非平凡臨界點.

2 主要結(jié)論及證明

引理4[6]假設(shè)(H1)及(H2)滿足,那么存在M∞＞0使得,

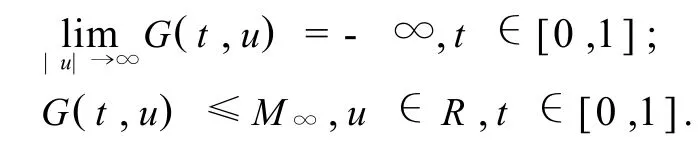
取{un}∈L2[0,1],使得 ‖un‖→∞,且有J(un)≤C,其中,C ∈R為常數(shù).定義 vn= un/‖un‖,取其子列不妨仍記為{vn},使得存在 v0∈L2[0,1],有{vn}弱收斂到 v0,且 ‖v0‖≤1.同時,由 K1/2的全連續(xù)性知,K1/2vn→K1/2v0于 L2[0, 1],同時有,

引理5 假設(shè)(H1)及(H2)滿足,那么有:

(i)J在L2[0,1]是強制的,即 J(u)→+ ∞,‖u‖→∞;

(ii)J滿足PS條件.

證明 (i)假設(shè)(H1)及(H2)滿足,令,

則由引理4知,

由上式知,

故,(Kv0,v0)=λ0‖v0‖2.v0=±ρ0e0,ρ ∈(0,1],K1/2v0(t)≠0,t∈[0,1],并有,

因此,當(dāng) n→∞時,

由上式的矛盾知假設(shè)不成立.因此,J在L2[0, 1]是強制的.

定理1 假設(shè) f(t,0)=0,對(H1)、(H2)和(H3)滿足,那么邊值問題至少有2個平凡解.

證畢.

3 應(yīng)用舉例

考慮邊值問題,

其中,

通過計算知,

[1]Liu B.Positive Solutions of Fourth-oder Boundary Value Problems[J].Appl Math Comput,2004,148(1):407-420.

[2]Pang C,Dong W,Wei Z.Multiple Solutions for Fourth-order Boundary Value Problem[J].J Math Anal Appl,2006,314(1): 464-476.

[3]Liu X,Li W.Existence and Multiplicity of Solutions for Fourth Order Boundary Value Problems with Parameters[J].J Math Anal Appl,2007,327(1):362-375.

[4]Yang Y,Zhang J.Existence of Solutions for Some Fourth-order Boundary Value Problems with Parameters[J].Nonlinear Anal, 2008,69(1):1364-1375.

[5]Han G,Xu Z.Multiple Solutions of Some Nonlinear Fourth-order Beam Equations[J].Nonlinear Anal,2008,68(1):3646-3656.

[6]黃永峰.一類帶參數(shù)的四階Neumann邊值問題解的存在性[J].昌吉學(xué)院學(xué)報,2011,26(1):104-108.

[7]郭大鈞.非線性泛函分析[M].濟南:山東科學(xué)技術(shù)出版社,2001.

[8]Chang K.Infinite Dimensional Morse Theory and Multiple Solution Problems[M].Boston:Birkhauser Press,1993.

[9]Li F,Liang Z,Zhang Q.Existence of Solutions of a Class of Nonliear Second Order Two-point Boundary Value Problems[J].J Math Anal Appl,2005,312(1):357-373.

[10]LiuJ.The Morse Index of a Saddle Point[J].Systems Sci Math Sci,1989(2):32-39.

[11]ZhangJ,Li S.Muitiple Nontrivial Solutions for Some Fourth Order Semlinear Elliptic Problems[J].Nonlinear Anal,2005,60 (1):221-230.