李明泉

(三峽大學(xué)理學(xué)院,湖北宜昌 443002)

復(fù)對數(shù)函數(shù)是實(shí)對數(shù)函數(shù)在復(fù)數(shù)域內(nèi)的拓廣,拓廣后的復(fù)對數(shù)函數(shù)既保持了實(shí)對數(shù)函數(shù)的一些基本性質(zhì),同時(shí)又獲得了一些新的特性,這是在教學(xué)中應(yīng)該特別提醒學(xué)生的.例如,設(shè)z1,z2是不為 0的復(fù)數(shù),則:

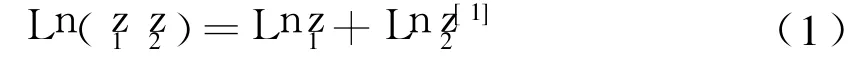
式(1)在復(fù)數(shù)范圍內(nèi)仍成立.由于復(fù)對數(shù)函數(shù)是無窮多值函數(shù),因此式(1)要理解為等式兩端值的全體是相同的,即對式(1)左端的任一值,在式(1)右端都可以找到一值與之相等,反之亦然.

設(shè)z是不為0的復(fù)數(shù),考慮等式:

容易看出式(2)在復(fù)數(shù)范圍內(nèi)不再成立.

式(1)還可以加以推廣,設(shè)復(fù)數(shù) zi≠0 (i=1,2,…,n),則:

特殊的,當(dāng)zi=z≠0(i=1,2,…,n)時(shí),式(3)成為:

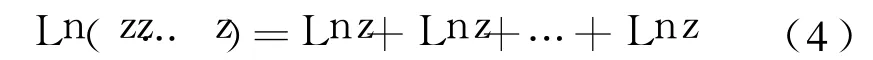
顯然式(4)可記為:

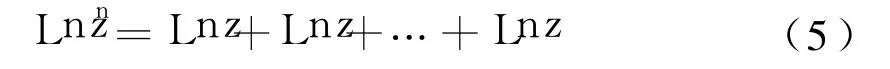
值得注意的是式(5)右端不能記為:

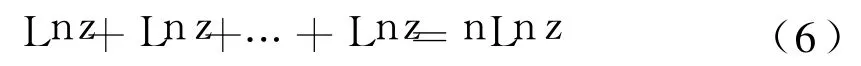
否則式(5)成為式(2),因此式(6)在復(fù)數(shù)域內(nèi)是不成立的.再舉一個(gè)具體例子來說明式(6)不成立,例如,取z=1,當(dāng)n=2時(shí),由式(6)得Ln1+Ln1=2Ln1[2],即:In|1|+ i(arg1+2kπ)+In|1|+i(arg1+2mπ)=2[In |1|+i(arg1+2nπ)],也就是2kπi+2mπi= 4nπi(其中k,m,n為整數(shù)),當(dāng)k=0,m=1時(shí),左端的值為 2πi,顯然不存在整數(shù) n的值,使得2πi=4nπi.

由于Lnz的主值Inz=In|z|+iargz為一單值函數(shù),因此式(6)對主值Inz是成立的,即:

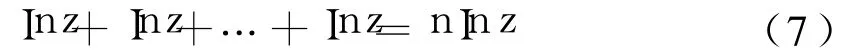
通過以上的分析可以得出結(jié)論:式(6)在復(fù)數(shù)域內(nèi)不成立,而式(7)是成立的.

1 對一個(gè)證明的不妥之處的糾正

由西安交通大學(xué)高等數(shù)學(xué)教研室編寫的《復(fù)變函數(shù)》(第 4版)是目前較流行的一本工科復(fù)變函數(shù)教材,很多高校都把該教材作為工科專業(yè)的教科書,該書在講授 a與 b的乘冪ab=ebLna時(shí)指出:當(dāng)a是不為0的復(fù)數(shù),而b為正整數(shù)n時(shí),a與b的乘冪就是通常意義的 a的n次冪,即an=a·a…a,其證明如下:

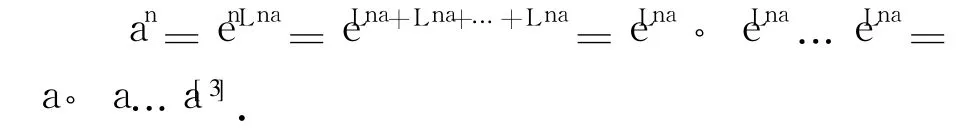
該證明過程顯然用到了式(6),這是不妥當(dāng)?shù)?很容易讓讀者誤認(rèn)為式(6)是成立的,比較合理的證明為:an=enLna=en(Ina+2kπi)= enIna+2knπi(其中 k為整數(shù)).由于復(fù)變指數(shù)函數(shù)是以 2πi為周期的周期函數(shù),因此有 an= enIna,再由式(7)得:

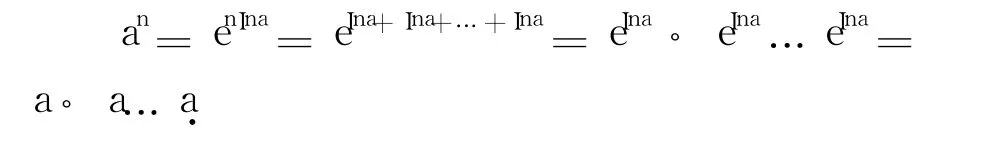
[1] 鐘玉泉.復(fù)變函數(shù)學(xué)習(xí)指導(dǎo)書[M].北京:高等教育出版社,2004

[2] 余家榮.復(fù)變函數(shù)[M].北京:人民教育出版社, 1979

[3] 西安交通大學(xué)高等數(shù)學(xué)教研室.復(fù)變函數(shù)[M]. 4版.北京:高等教育出版社,2003