Solubility of Paclitaxel in Mixtures of Dichloromethane and Supercritical Carbon Dioxide*
LUO Nin (羅寧), LU Yingmei (盧英妹) and JIANG Yanbin (江燕斌),,**
12 Star Lake Bioscience Co., Inc., Zhaoqing 526040, China School of Chemistry and Chemical Engineering, South China University of Technology, Guangzhou 510640, China
1 INTRODUCTION
Paclitaxel is a kind of diterpenoid compound separated from bake of yew trees. Presently it is one of the most popular and promising anti-cancer agents for breast and ovarian cancers [1]. The current clinical formulation of paclitaxel using Cremophor EL as solvent usually elicits serious hypersensitivity in patients[2]. In order to reduce side-effects and increase therapeutic efficiency, many efforts have been devoted to develop Cremophor EL free drug delivery system [3].
Supercritical anti-solvent process becomes an attractive technique of preparing drug delivery system with CO2as favorite anti-solvent and dichloromethane(DCM) as cosolvent [4, 5]. And in recent years, drug delivery system of paclitaxel is successfully prepared by using supercritical anti-solvent method [6]. During supercritical anti-solvent process, the particle morphology and size distribution are strongly affected by the phase behavior [7, 8], and thus it is crucial to understand the phase behavior of supercritical anti-solvent systems. Although a large amount of investigation has been carried out in recent years on the phase behavior of supercritical systems, there is still a lack of equilibrium data.
In this study, the solubility data of paclitaxel + CO2+DCM system were measured using a high-pressure phase equilibrium apparatus equipped with a variable volume view cell. Three widely used cubic equations of state [Redlich-Kwong (RK), Soave-Redlich-Kwong(SRK) and Peng-Robinson (PR) EOS] coupled with the classical van der Waals one-fluid mixing rules are selected to correlate the experimental data since they are applicable to many mixtures containing supercritical fluids [9]. The aim of this work is to present fundamental solubility and thermodynamics data for preparation and quality control of drug delivery system of paclitaxel using supercritical anti-solvent process.
2 EXPERIMENTAL
2.1 Materials
Paclitaxel with stated mass fraction purity >0.998 was obtained from Jinhe Bio-Technology Co. Ltd.,China. The molecular mass of paclitaxel is 853.92 and its molecular structure is described in Fig. 1. Analytical grade DCM (mass fraction >0.995) used as solvent was purchased from Guangdong Guanghua Chemical Reagents Co., China. CO2(mass fraction >0.999) used as anti-solvent was purchased from Guangzhou Shengying Gas Co. Ltd., China. All of them were used directly without further purification.
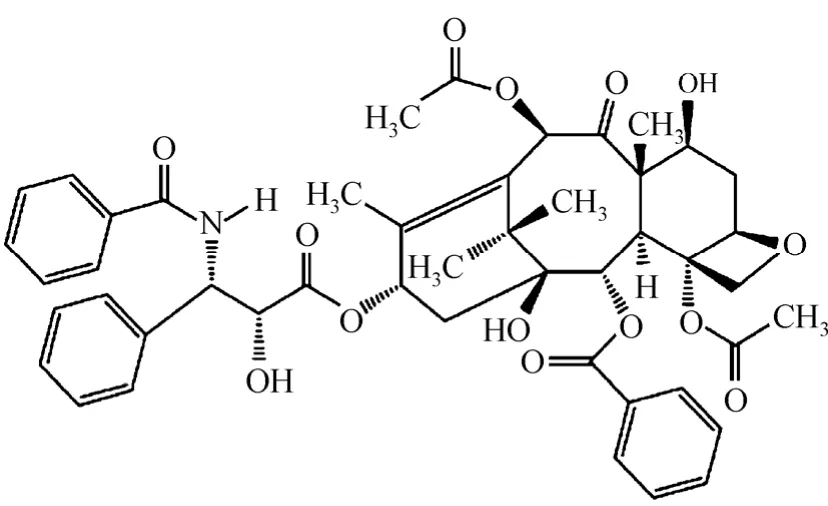
Figure 1 Molecular structure of paclitaxel
2.2 Apparatus and procedure
The experimental apparatus for measuring phase behavior data of different systems is the same as that described in Gong and Cao [10],i.e., the supercritical phase monitor (SPM20, Thar Technology Co., Ltd.). It contains several main parts, that is, (1) a programmable logic controller (PLC) control panel; (2) a high-pressure variable-volume view cell with a pressure transmitter and an internal working volume of about 20 ml; (3) a movable piston inside the cell to change its volume by a hydraulic hand pump and thus change the pressure of the system; (4) an electric heater pads along with high-precision thermocouples for temperature measurement in the cell; (5) a sapphire window coupled with a charge-coupled-device (CCD) camera which is connected to a computer for observing and recording experimental phenomenon; and (6) a stirring system equipped on the top of the cell for agitating the solution in high pressure and sealing the cell. Its maximum operating pressure and temperature are 40.0 MPa and 423.1 K when stirring. The pressure and temperature of the monitor were measured with a resolution of 0.01 MPa and 0.1 K, respectively.
To obtain solubility of paclitaxel in the supercritical systems of CO2+ DCM, experiments were carried out as the following procedure, which is similar to Ohet al. [5] and Jianget al[11]. First, the piston was located to adjust the volume equal to that of solution about 5 ml to remove the entrapped air in the cell,and the solution with a desired composition of paclitaxel and DCM was measured by an electronic balance (AL104, Mettler Toledo) with an uncertainty of 0.1 mg and loaded into the cell. Then, the cell with the stirring system was sealed, the piston was loosened, and about 17.5 g CO2, which depended on the desired mass fraction of CO2and was determined by mass flowmeter (MASS 6000, Siemens) with a precision of 0.1 g, was injected into the cell. The mass fraction of paclitaxel in the paclitaxel + CO2+ DCM system is from 0.0010 to 0.0058, and the mass fraction of DCM content in the solution changes from 0.24 to 0.28.
The mixture in the cell was compressed and heated to a desired temperature. Simultaneously, the water in the hydraulic hand pump was compressed to displace the piston to the window side to decrease the cell volume and thus to raise the pressure in the cell.As the pressure increased and the system was well agitated by the stirring system, the mixture of paclitaxel + CO2+ DCM became a homogeneous solution.After the system reached thermal equilibrium and its temperature was stable enough, the pressure was slowly reduced by about 0.5 MPa·min-1until the single-phase solution became cloudy [5, 11]. The cloud point indicates that the solute begins to precipitate and is defined as the pressure at which the stirrer is no longer to be visually observed [5, 11]. Each point was repeated three times for its mean value and reliable result. The system temperature was from 313.1 to 343.1 K with each point increment of about 5 K. As the above procedure repeated, the pressure-temperature(p-T) cloud point curves for the two systems were obtained.
2.3 Verification
Cloud-point pressures of Poly (lactic acid) with molar mass of 50 kg·mol-1in supercritical mixtures of DCM and CO2were measured to verify the reliability of the experimental apparatus and procedure. The experimental cloud-point pressures were compared with data reported by Leeet al[4]. The obtained data were in reasonable agreement with an average absolute relative deviation of 2.39%, indicating the reliability of the apparatus and procedure [11].
3 RESULTS AND DISCUSSION
3.1 Experimental data
Experimental data of paclitaxel + CO2+ DCM system are given in Table 1. The cloud point pressures(p) were determined as a function of temperature (T)from 313.1 to 343.1 K, pressure up to 33.52 MPa and paclitaxel content. As shown in Table 1, the mass fraction of paclitaxel (w2) varies from 0.0010 to 0.0058 to determine the solubility of paclitaxel in mixtures of DCM and CO2, and the mass fraction of DCM (w3) in the solution changes from 0.24 to 0.28. The uncertainties ofpandTare 0.01 MPa and 0.1 K, respectively.
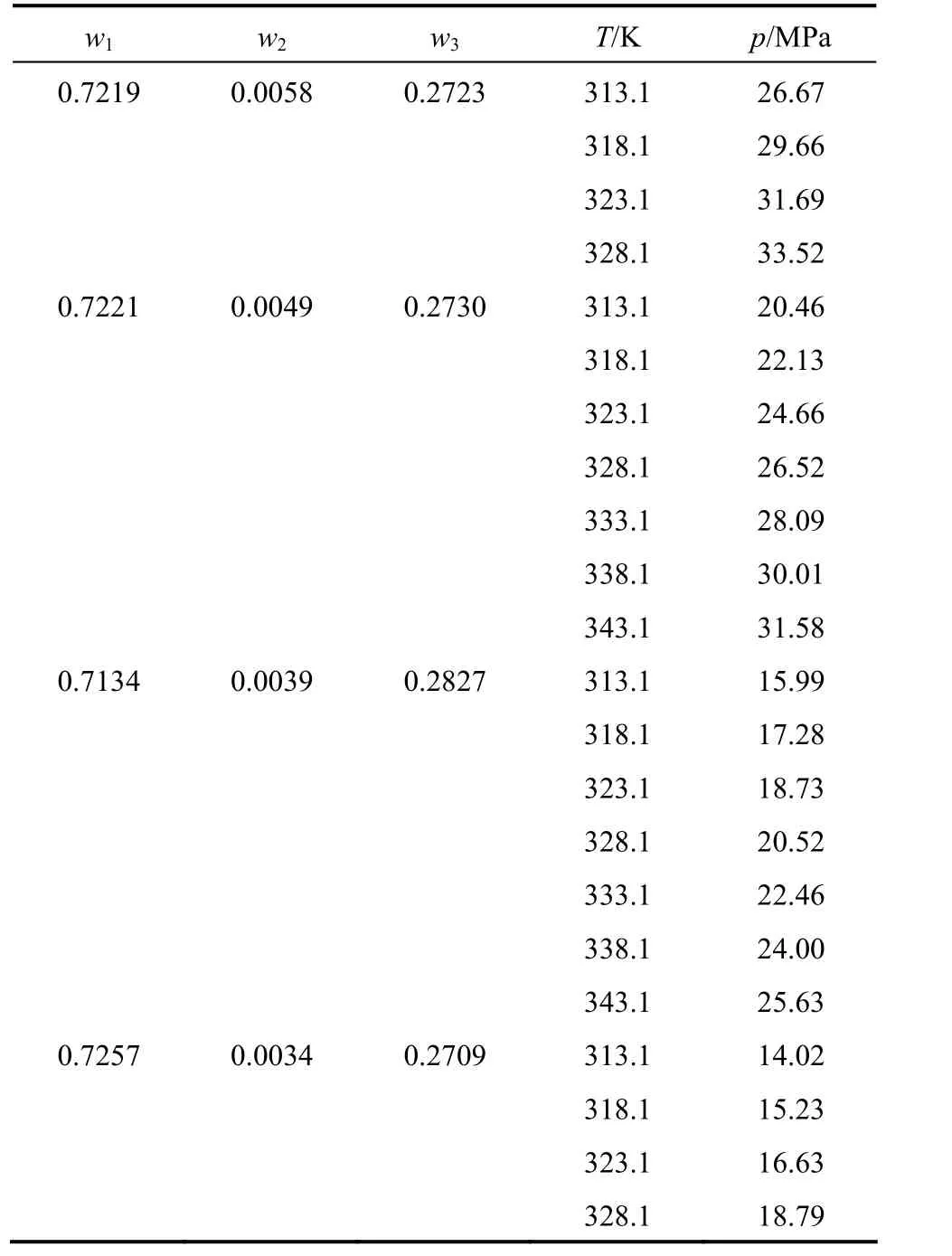
Table 1 Experimental mass fraction data of cloud points of paclitaxel (2) in CO2 (1) + DCM (3)

Table 1 (Continued)

Figure 2 p-Tisopleths of cloud point for paclitaxel (2) in CO2 (1) + DCM (3) at different paclitaxel contentsw2: ■ 0.0010; □ 0.0015; ● 0.0022; ○ 0.0024; ▲ 0.0029;△ 0.0034; ◆ 0.0039; ◇ 0.0049; ▼ 0.0058
Figure 2 shows thep-Tisopleths of the cloud points for paclitaxel in the mixed solvents at different mass fraction of paclitaxel. As shown in Fig. 2, above each cloud point curve it is the region of single phase,while double phases below the curve. This indicates that the cloud points are the boundary of phase transition, and paclitaxel is completely soluble in DCM and CO2in the region of single phase. Thus, mass fraction of paclitaxel at the cloud point is its solubility in the solvent mixture. It is obviously seen from Fig. 1 that the cloud point pressure increases with increasing temperature, which indicates that the ternary system exhibits a typical Lower Critical Solution Temperature(LCST) behavior. It can also be described that as temperature increases, it requires higher pressure to maintain the solution in a single phase.
At a given temperature, as shown in Fig. 2, increasing paclitaxel content and decreasing DCM content will increase the pressure at the cloud point and shrink the region of single phase. Because the solubility of paclitaxel in DCM is limited, as mass fraction of paclitaxel increases, the solute trends to being supersaturated. The cloud point pressure increases linearly with a logarithmic increase of paclitaxel content.
Solubility of paclitaxel (w2) as a function of cloud point pressure at seven different temperatures is shown in Fig. 3. Curves ofp-w2are simulated by fitting the experimental data with cubic polynomial, and the correlation coefficients areR2>0.99. At a fixed temperature, solubility of paclitaxel in mixtures of DCM and CO2is increased along with increase of system pressure. Thus, solubility of paclitaxel in the ternary system can be promoted by increasing pressure. Besides, lower solubility of paclitaxel can be obtained at higher temperature by decreasing pressure.

Figure 3 Solubility of Paclitaxel (2) in mixtures of CO2 (1) +DCM (3) as a function of pressure at different temperatures T/ K: ■ 313.1; □ 318.1; ▲ 323.1; △ 328.1; ● 333.1; ○ 338.1;◆ 343.1

Table 2 Thermodynamic properties of paclitaxel
3.2 Data correlation
Although many equations of state (EOS) have been appeared in the literature, only a few of them have been found to be promising for the estimation of supercritical solubility [9]. Three successful cubic equations of state,i.e., Redlich-Kwong equation of state (RK EOS) [12], Soave-Redlich-Kwong equation of state (SRK EOS) [13] and Peng-Robinson equation of state (PR EOS) [14], which are widely used for strongly nonideal systems with limited miscibility, are selected to correlate the experimental data.
RK EOS is presented as follows:

wherevis the molar volume (m3·mol-1),pis the experimental pressure (Pa),Tis the experimental temperature (K), andaandbare parameters.aandbvalues of the pure component depend on:

whereTcis the critical temperature (K) andpcis the critical temperature pressure (Pa).
SRK EOS is shown as follows:


The pure-component parameters (aiiandbii) are calculated from critical properties of the pure fluids.Critical properties of CO2and DCM can be obtained from many literatures conveniently. Because of limited knowledge, there are no adequate physical properties available for paclitaxel. The critical temperature and pressure are estimated using group contribution techniques based on its molecular structure [15]. The vapor pressure of paclitaxel is estimated using the method suggested by Gupta,et al[16]. Thermodynamic properties of paclitaxel are listed in Table 2.
To extend these EOS to mixtures, a combination of mixing and combining rules is generally used [17].It is found that the van der Waals one-fluid mixing rules with two adjustable parameters are superior to some other more complicated mixing rules. The classical van der Waals one-fluid mixing rules are:

and

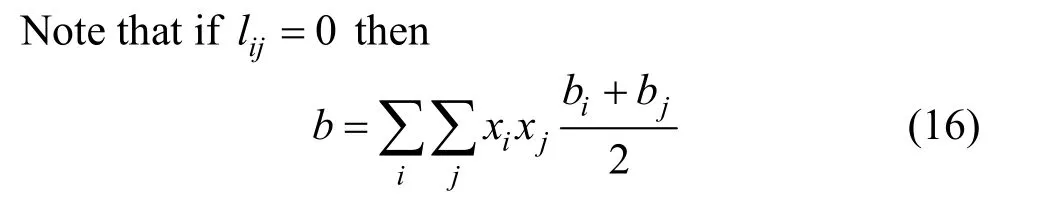
wherekij,lijare the binary interaction parameters. For each temperature, the binary interaction parameterskijandlijare determined by least square fitting of the experiment data in Table 1 to minimize the following objective function:

whereix,calixare the experimental and calculated mole fraction of componenti, respectively. The quality of fitting effect is expressed in terms of average relative deviation (ARD):

whereNis the number of experimental data.
The regressed results of interaction parameterskij,lijand ARD (%) of six combined models along with different temperatures are shown in Table 3. For all of the equations of state, fitting precisions obtained with two binary interaction parameterskijandlijare superior to those with only one binary interaction parameterkij(i.e.,lij=0), with ARD<6% and >11.5%, respectively.This indicates that mixing rules have greater impact on correlation accuracy than the equations of state,which means fitting effects of different models mainly depend on selection of mixing rules. The accuracy of predicted solubility values can be greatly improved by introducing the secondary parameterlij. Among the three equations of state, RK and SRK give better results in correlating solid-supercritical fluid equilibrium, while PR EOS has been usually used in predicting vapor-liquid equilibrium [9].
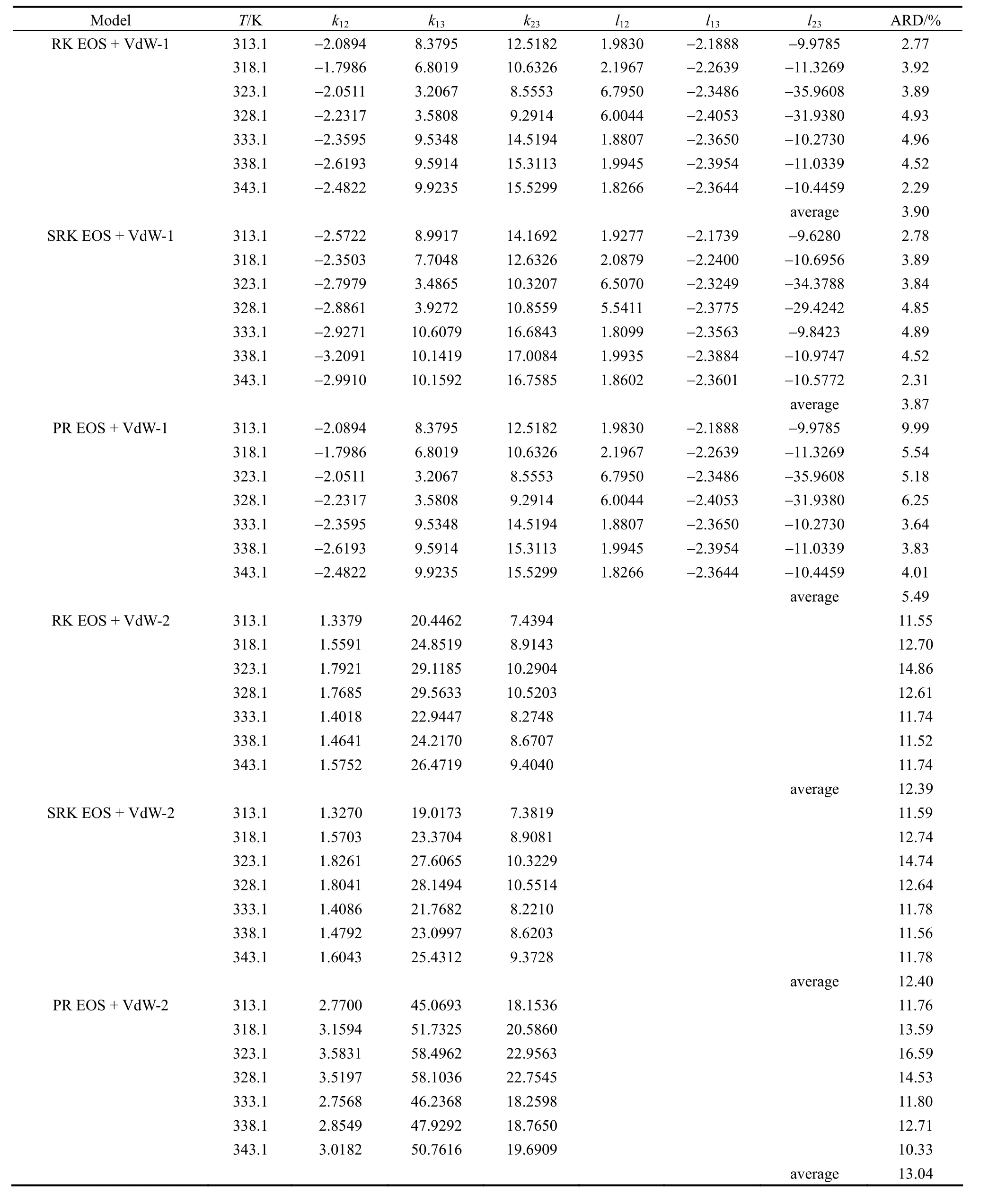
Table 3 Binary interaction parameters and ARD (%) of different combined models
SRK EOS coupled withkijandlijshows the best fit of this ternary system with ARD <5%. The best regressed results of interaction parameterskij,lijand ARD along with different temperatures are shown in Table 3. The results of SRK EOS coupled withkijare listed for comparing. It can be seen that absolute values ofkijandlijare all greater than 1, which means that these adjustable parameters represent the common influence factor of solubility calculation, for instance,critical properties, vapor pressure and cosolvent inducing [18]. To our best knowledge, because of the complexity comparing with the normal system, data correlation of the supercritical system using EOS is still a challenge up to now, and thus much effort must be devoted into this subject to get better correlation results in the future. Fig. 4 shows the comparison of experimental solubility along with calculated results of SRK EOS withkijandlij(solid line) and SRK EOS with onlykij(i.e.,lij=0) (dotted line), respectively. It indicates that the solubility of paclitaxel (2) in CO2(1) +DCM (3) can be satisfactorily estimated by using SRK EOS coupled withkijandlij.

Figure 4 Comparison of experimental solubility with calculated results□ 318.1 K, exp.; ○ 328.1 K, exp.; △ 338.1 K, exp.;SRK EOS + kij and lij, cal.; SRK EOS + kij, cal.
4 CONCLUSIONS
The solubility of paclitaxel in solvent mixtures of DCM and supercritical CO2was investigated as a function of temperature, pressure and the paclitaxel content by measuring the cloud points of the ternary mixture. In thep-Tisopleths of cloud points, the cloud point pressure increases with increasing temperature,which exhibits a typical LCST behavior of the system.Increasing the paclitaxel content at a given temperature will increase the cloud point pressure and shrink the single phase region. The three cubic equations of state with the van der Waals one-fluid mixing rules with two adjustable parameters are selected to correlate the experimental solubility of paclitaxel in DCM + CO2mixtures. SRK EOS coupled with two binary interaction parameterskijandlijshows the best fit of this ternary system with ARD <5%. The correlation accuracy can be greatly improved by introducing the secondary parameterlij.
NOMENCLATURE

ACKNOWLEDGEMENTS
The authors are also grateful to Dr.J. Guan for the helpful discussion of the program.
1 Rowinsky, E.K., Cazenave, L.A., Donehower, R.C., “Taxol: A novel investigational antimicrotubule agent”,J.Natl.Cancer I., 82 (15),1247-1259 (1990).
2 Gelderblom, H., Verweij, J., Nooter, K., Sparreboom, A., “Cremophor EL the drawbacks and advantages of vehicle selection for drug formulation”,Eur.J.Cancer, 37 (13), 1590-1598 (2001).
3 Panchagnula, R., “Pharmaceutical aspects of paclitaxel”,Int.J.Pharm., 172 (1-2), 1-15 (1998).
4 Lee, B.C., Kuk, Y.M., “Phase behavior of poly (L-lactide) in supercritical mixtures of dichloromethane and carbon dioxide”,J.Chem.Eng.Data, 47 (2), 367-370 (2002).
5 Oh, D.J., Lee, B.C., Hwang, S.J., “Solubility of simvastatin and lovastatin in mixtures of dichloromethane and supercritical carbon dioxide”,J.Chem.Eng.Data, 52 (4), 1273-1279 (2007).
6 Kang, Y.Q., Wu, J., Yin, G.F., Huang, Z.B., Liao, X.M., Yao, Y.D.,Ouyang, P., Wang, H.J., Yang, Q., “Characterization and biological evaluation of paclitaxel-loaded poly (L-lactic acid) microparticles prepared by supercritical CO2”,Langmuir, 24 (14), 7432-7441(2008).
7 Miguel, F., Martin, A., Gamse, T., Cocero, M. J., “Supercritical antisolvent precipitation of lycopene: Effect of the operating parameters”,J.Supercrit.Fluids, 36 (3), 225-235 (2006).
8 Matsuyama, K., Mishima, K., “Phase behavior of CO2+ polyethylene glycol + ethanol at pressure up to 20 MPa”,Fluid Phase Equilib.,249 (1-2), 173-178 (2006).
9 Lee, Y.Y., Kim, H., Lee, H., Hong, W.H., “One-fluid mixing rules for cubic equations of state: I. Solubility of pure solids in supercritical fluids”,Korean J.Chem.Eng., 5 (1), 76-82 (1988).
10 Gong, X.Y., Cao, X.J., “Measurement and correlation of solubility of artemisinin in supercritical carbon dioxide”,Fluid Phase Equilirb.,284 (1), 26-30 (2009).
11 Jiang, Y.B., Liu, M., Sun, W.L., Li, L.X., Qian, Y., “Phase behavior of poly(lactic acid)/poly(ethylene glycol)/poly(lactic acid) (PLAPEG-PLA) in different supercritical systems of CO2+ Dichloromethane and CO2+ C2H5OH + dichloromethane”,J.Chem.Eng.Data, 55(11), 4844-4848 (2010).
12 Redlich, O., Kwong, J.N.S., “On the thermodynamics of solutions. V.an equation of state. fugacities of gaseous solutions”,Chem.Rev., 44,233-244 (1949).
13 Soave, G., “Equilibrium constants from a modified Redlich-Kwong equation of state”,Chem.Eng.Sci., 27 (6), 1197-1203 (1972).
14 Peng, D.Y., Robinson, D.B., “A new two-constant equation of state”,Ind.Eng.Chem.Fundam., 15 (1), 59-64 (1976).
15 Nalesnik, C.A., Hansen, B.N., Hsu, J.T., “Solubility of pure taxol in supercritical carbon dioxide”,Fluid Phase Equilibr., 146 (1-2),315-323 (1998).
16 Gupta, P.K., Ganesan, K., Gutch, P.K., Manral, L., Dubey, D., “Vapor Pressure and Enthalpy of Vaporization of Fentanyl”,J.Chem.Eng.Data, 53 (3), 841-845 (2008).
17 Shibata, S.K., Sandler, S.I., “Critical evaluation of equation of state mixing rules for the prediction of high-pressure phase equilibria”,Ind.Eng.Chem.Res., 28 (12), 1893-1898 (1989).
18 Li, Z.Y., Meng, T.Y., Deng, X.L., Liu, X.W., Xia, Y.J., Hu, D.P.,“Correlating and predicting the effects of cosolvent on the solubility enhancement of solids in supercritical carbon dioxide”,Comput.Appl.Chem., 24 (6), 831-837 (2007).
 Chinese Journal of Chemical Engineering2011年4期
Chinese Journal of Chemical Engineering2011年4期
- Chinese Journal of Chemical Engineering的其它文章
- Synthesis of Methyl Isopropyl Ketone and Diethyl Ketone over Ni-Na/ZrO2-MnO2-ZnO Catalyst*
- Isotherm Equation Study of F Adsorbed from Water Solution by Fe2(SO4)3-modified Granular Activated Alumina*
- Preparation and Dyeing Performance of a Novel Crosslinking Polymeric Dye Containing Flavone Moiety*
- The Kinetics for Electrochemical Removal of Ammonia in Coking Wastewater*
- Solvent Recovery from Soybean Oil/Hexane Miscella by PDMS Composite Membrane*
- Direct Optical Resolution of Chiral Pesticides by High Performance Liquid Chromatography*
