A Penalty Approach for Generalized Nash Equilibrium Problem?
HOU JIANAND LAI JUN-FENG
(1.School of Mathematical Sciences,Dalian University of Technology,Dalian,Liaoning,116024)
(2.Science College,Inner Mongolia University of Technology,Hohhot,010051)
A Penalty Approach for Generalized Nash Equilibrium Problem?
HOU JIAN1AND LAI JUN-FENG2
(1.School of Mathematical Sciences,Dalian University of Technology,Dalian,Liaoning,116024)
(2.Science College,Inner Mongolia University of Technology,Hohhot,010051)
The generalized Nash equilibrium problem(GNEP)is a generalization of the standard Nash equilibrium problem(NEP),in which both the utility function and the strategy space of each player depend on the strategies chosen by all other players. This problem has been used to model various problems in applications.However,the convergent solution algorithms are extremely scare in the literature.In this paper, we present an incremental penalty method for the GNEP,and show that a solution of the GNEP can be found by solving a sequence of smooth NEPs.We then apply the semismooth Newton method with Armijo line search to solve latter problems and provide some results of numerical experiments to illustrate the proposed approach.
Nash equilibrium problem,generalized Nash equilibrium problem,logarithmic barrier function,quasi-variational inequality,semismooth Newton method
1 Introduction
We consider the generalized Nash equilibrium problem.We first recall the de fi nition of the Nash equilibrium problem.Let N be the number of players,and each player ν∈{1,···,N} control a variable xν∈Rnν.All players’strategies are collectively denoted by a vector x=(x1,···,xN)T∈Rn,where n=n1+···+nN.To emphasize the ν-th player’s variables within the vector x,we sometimes write x=(xν,x?ν)T,where x?ν∈Rn?νsubsumes all the other players’variables.
Let θν:Rn→Rbe the ν-th player’s payo ff(or loss or utility)function,and Xν?Rnνbe the strategy set of the player ν.Then x?=(x?,1,···,x?,N)T∈Rnis called a Nash equilibrium,or a solution of the standard Nash equilibrium problem(NEP),if each blockcomponent x?,νis a solution of the optimization problem:
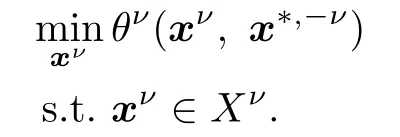
The generalized Nash equilibrium problem(GNEP)generalizes the situation to some extent since now the strategy of player ν belongs to a set Xν(x?ν)?Rnνthat depends on the rival players’strategies.The aim of each player ν,giving the other players’strategies x?ν,is to choose a strategy xνthat solves the minimization problem:

A vector x=(xν)Nν=1is said to be feasible to the GNEP if xν∈Xν(x?ν)for all ν.The GNEP is the problem to find a feasible point x?such that each player’s strategy x?,νsatis fies
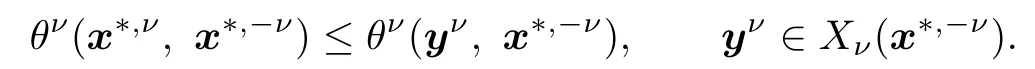
Such a vector x?is called a generalized Nash equilibrium or a solution of the GNEP.
Since Arrow and Debreu’s paper[1]on the existence of equilibria for a competitive economy was published,NEPs and GNEPs have been the subject of a constant if not intense interest.Especially in recent years,the GNEP has been used to model a host of interesting problems arising in economy,computer science,telecommunications and deregulated markets (for example,see[2–4]).
Numerical methods for the GNEP have been developed with different objectives and problem settings.Motivated by the fact that a standard NEP can be reformulated as a variational inequality problem(VI)(see[5–6]),Harker[7]also gave a reformulation of the GNEP as a quasi-variational inequality(QVI).It was noted in[8]that the normalized Nash equilibria which is a solution of the GNEP can be found by solving a suitable standard VI associated to the GNEP.This method seems to be promising because we can find a solution of the GNEP by solving a single VI.The obtained solution is a particular equilibrium. In general,a GNEP has multiple or even in finitely many solutions,and therefore,the VI reformulation fail to identify some important GNEP solutions.
The penalization approach to GNEPs was initiated very recently by Fukushima and Pang[9].The idea of using an exact penalty approach by which a single nondifferentiable NEP has to be solved to obtain a solution of the GNEP was first put forward in[10],in a rather sketch way.This topic has recently been considered also by Fukushima[11],Facchinei and Kanzow[12].They gave some conditions under which penalty approaches can be used to find a generalized Nash equilibrium.
In this paper,by using the logarithmic barrier function and quadratic penalty terms, we transform a class of GNEPs which have shared equality constraints into a sequence of NEPs and show that a solution of the GNEP can be found under suitable conditions.Next, we apply the semismooth Newton method to solve latter NEPs.Finally,we present some numerical results to illustrate the proposed approach.
We use the following notations throughout the paper.For a differentiable function g:Rn→Rm,the Jacobian matrix of g at x∈Rnis denoted by Jg(x),and its transpose by?g(x).Given a differentiable functionΨ:Rn→R,the symbol?xνΨ(x)denotes the partial gradient with respect to xν-part only,andΨ(x)denotes the second order partial derivative with respect to xν-part and xμ-part.For a function f:Rn×Rn→R, f(x,·):Rn→Rdenotes the function with x being fixed.For vectors x,y∈Rn,hx,yi denotes the inner product de fi ned by hx,yi:=xTy and x⊥y implies hx,yi=0.If X?Rnis a nonempty closed convex set,we denote by
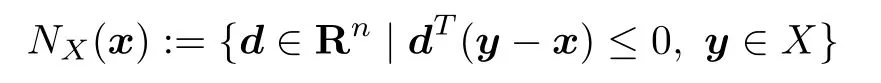
the normal cone to X at x∈X.
2 Problem Reformulation and Assumptions
Let F:Rn→Rmbe a locally Lipschitz continuous function.By Rademacher’s theorem,F is differentiable almost everywhere.Let DFdenote the set of points where F is differentiable. Then the Bouligand-subdifferential of F at x is given by(see[13])
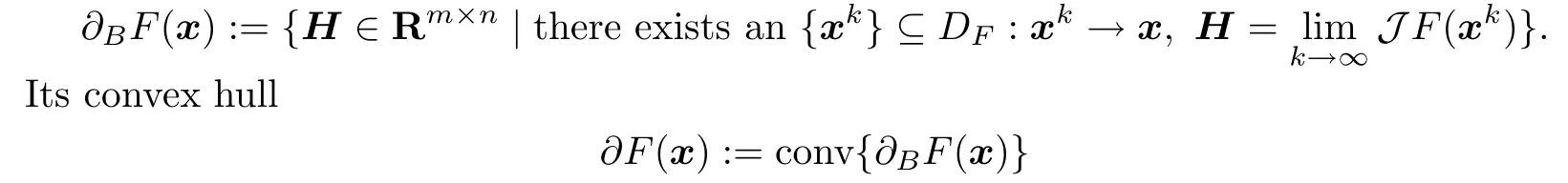
is Clark’s generalized Jacobian matrix of F at x(see[14]).
Based on this notation,we next recall the de fi nition of a semismooth function.This concept was firstly introduced by Mifflin[15]for real-valued mappings and extended by Qi and Sun[16]to vector-valued mappings.
De fi nition 2.1Let Φ:O?Rn→Rmbe a locally Lipschitz continuous function on an open setO.We say that Φ is semismooth at a pointx∈Oif the following conditions hold:
(i)Φ is directionally differentiable atx;
(ii)for any?x∈RnandV∈?Φ(x+?x),as?x→0,
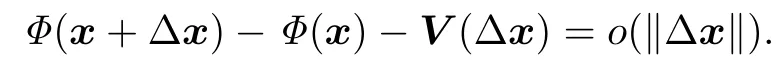
Furthermore,Φ is said to be strongly semismooth atx∈Oif Φ is semismooth atxand for any?x∈RnandV∈?Φ(x+?x),as?x→0,
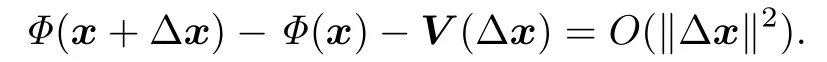
In the study on algorithms for locally Lipschitz systems of equations,the following regularity condition plays a role similar to which of the nonsingularity of the Jacobian matrix in the study of algorithms for smooth systems of equations.
De fi nition 2.2LetG:Rn→Rnbe Lipschitz aroundx.Gis said to be BD-regular atxif all the elements in?BG(x)are nonsingular.Ifˉxis a solution of the systemG(x)=0andGis BD-regular atˉx,thenˉxis called a BD-regular solution of this system.
The main difficulty of the GNEP stems from the variability of the feasible sets Xν(x?ν). If these feasible sets are actually fixed,i.e.,if Xν(x?ν)=Xνfor some given sets Xν, the problem reduces to a standard NEP which is a simpler problem.In this paper,we assume that the feasible set Xν(x?ν)of each player ν has the following structure.Let
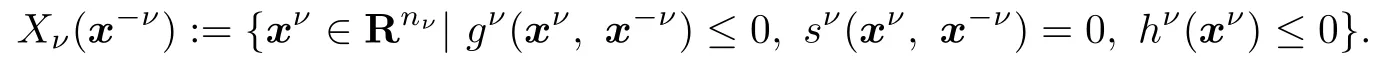
Then,each player ν has to solve the following optimization problem:
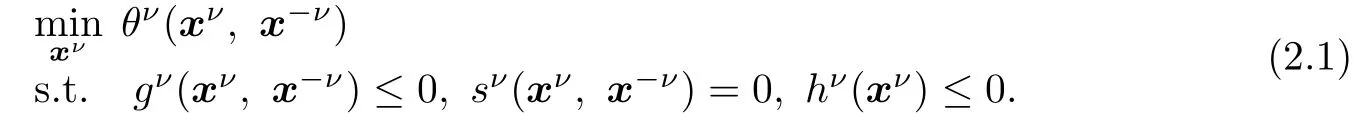
In the sequel,we make the following blanket assumptions,valid for all ν=1,···,N.

We call the problem(2.4)the penalized Nash equilibrium problem.
In the following section,we prove that a solution of the GNEP can be found by solving a sequence of problems of the type(2.4)under some suitable conditions.
3 Penalty Method for GNEP
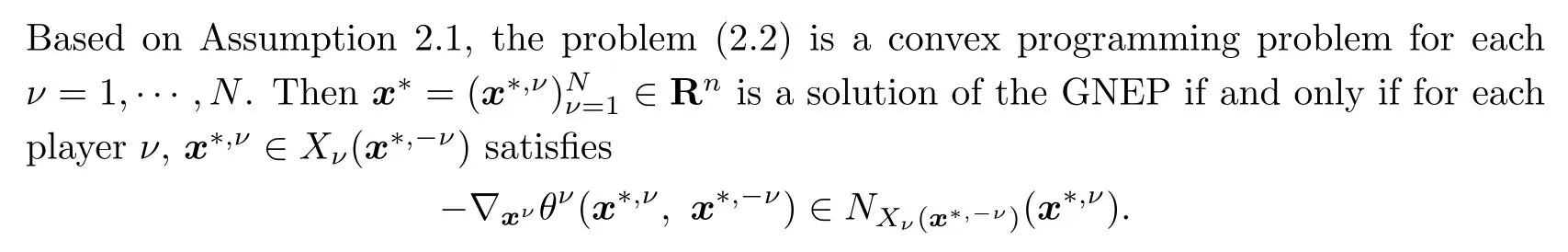

Noticing that the problem(2.4)is a convex programming problem,we have that a vector x∈X is a solution of this NEP if and only if for each ν,x satis fies
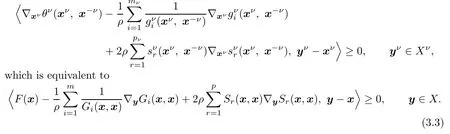
In order to give a convergence result of the penalty method,we first introduce a classical constraint quali fi cation:the extend Mangasarian-Fromovitz constraint quali fi cation (EMFCQ).

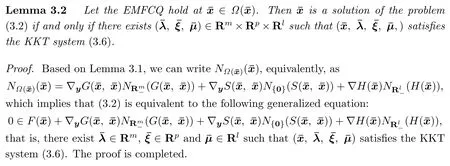
Now,we prove the following convergence theorem for our penalty approach.
Theorem 3.1Let{ρk}be a sequence of positive scalars which grows to in finite ask→∞. For eachk,letxkbe a solution of(3.3)withρ={ρk}.Suppose thatˉxis a limit point of the sequence{xk}at which the EMFCQ(3.4)holds.Thenˉxis a solution of the GNEP.

It is easy to see that γk?γ for k sufficiently large.Suppose that there is an in finite index setΥ?κ such that for every k inΥthe following holds:if
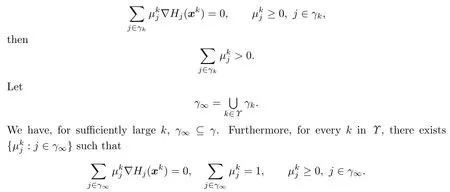

4 The Semismooth Newton Method and Numerical Results
In this section,a Nash equilibriumˉx of the problem(2.4)is computed by applying the semismooth Newton method(see[18])to the complementarity problem that represents the KKT conditions for(3.3)as follows:
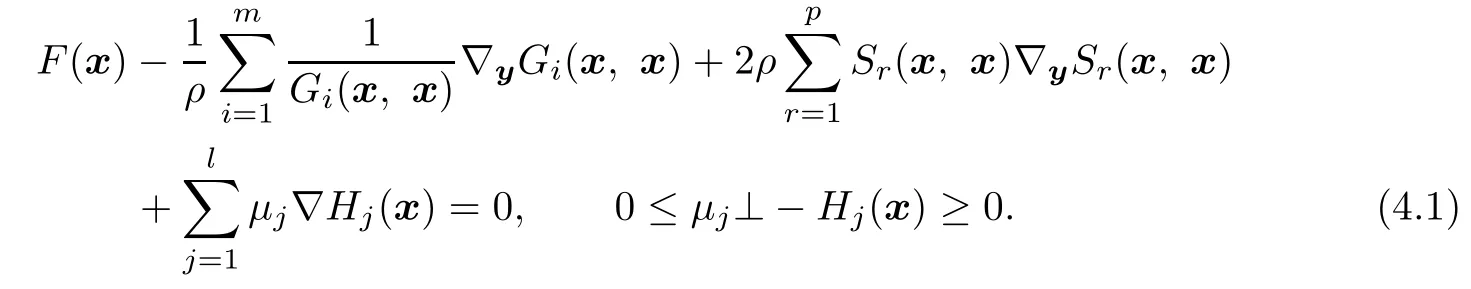
Using the Fischer-Burmeister(F-B)function
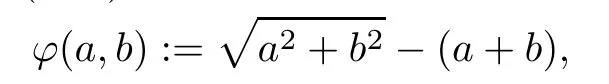
(4.1)can be reformulated as the system
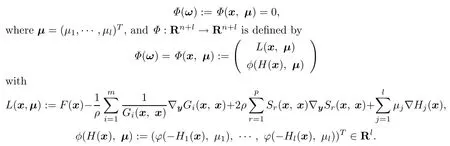
We describe the semismooth Newton method to the systemΦ(ω)=0 in the following, and in order to globalize it,the searching direction switchs to the steepest direction of the merit function

if the generalized Newton direction is not computable or does not satisfy a sufficient decrease condition.
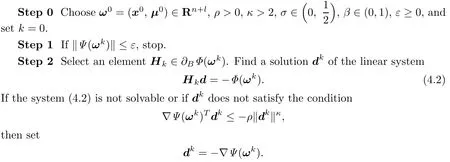
Algorithm 4.1Step 3Let tkbe the greatest number in{βj|j=0,1,2,···}such that
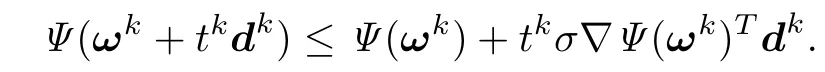
Step 4Set ωk+1=ωk+tkdk,k=k+1 and go back to Step 1.
The following result,summarizing the main properties of the algorithm,comes from[18] directly.
Theorem 4.1Let the sequence{ωk}be generated by Algorithm4.1and have a limit pointω?.Thenω?is a stationary point of Ψ.Furthermore,ifω?is a BD-regular solution of the system Φ(ω)=0,then{ωk}converges toω?Q-superlinearly.
We apply MATLAB 7.0 to some examples of the GNEP.The computational results are summarized in Tables 4.1 and 4.3.
Example 4.1This is a GNEP considered in[12].There are three players(N=3)having 3,2,and 2 variables,respectively.The objective function of each player is given by
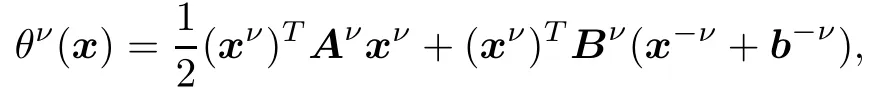
where the matrices and vectors involved are
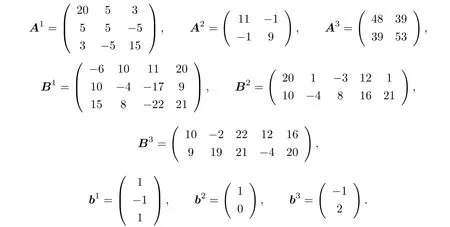
All of the variables have bound constraints:?10≤x≤10.In addition,the first player has the linear constraints

the second player has the constraints
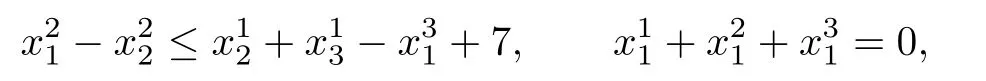
and the third player has the constraints
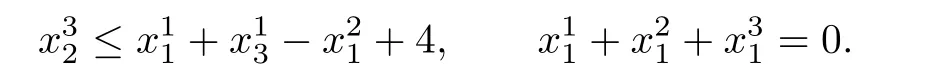
In Table 4.1 for the corresponding numerical results,we only state x11,x21and x31.
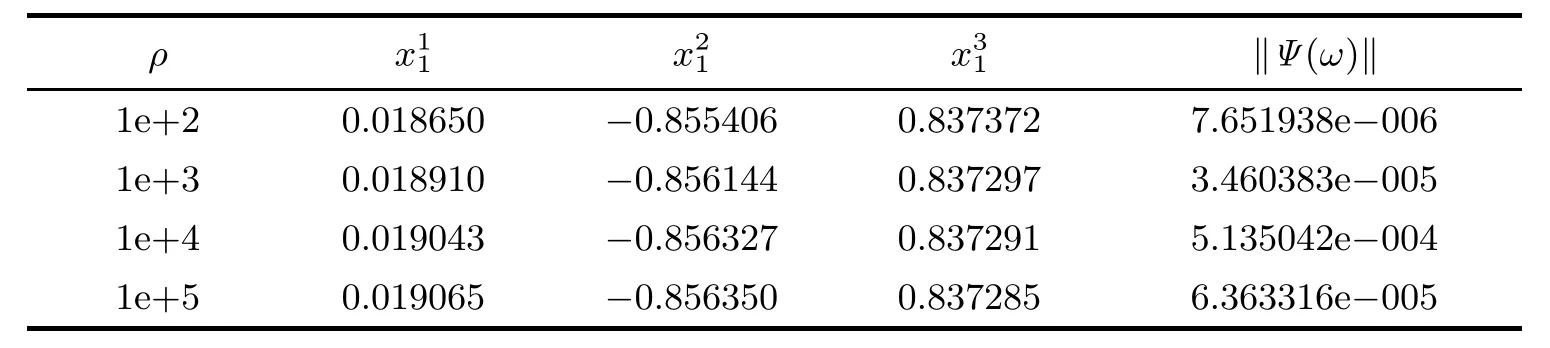
Table 4.1 Numerical results for Example 4.1
Example 4.2This GNEP from[19]is an electricity market problem.This model has three players,the player 1 controls a single variable x1∈R,the player 2 controls a twodimensional vector,and the player 3 controls a three-dimensional decision variable
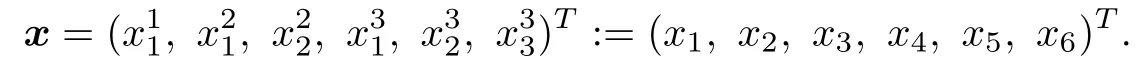
The utility functions are given by
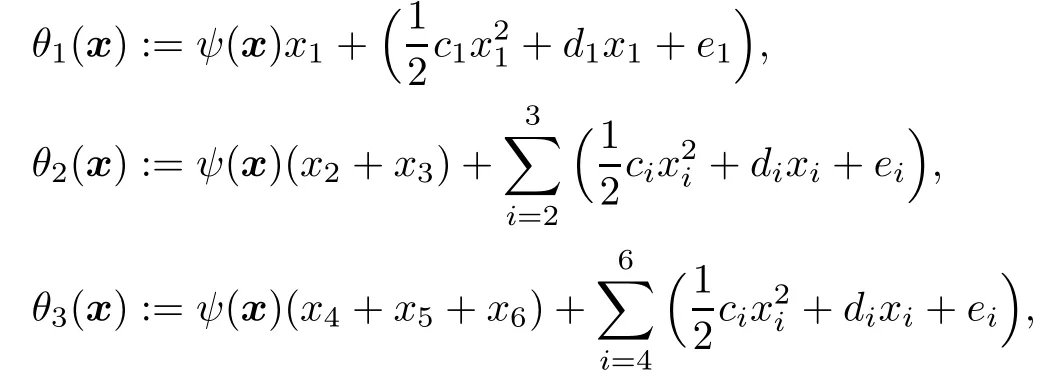
where ψ(x):=2(x1+···+x6)?378.4,and the constants ci,di,eiare given in Table 4.2.

Table 4.2 The constants ci,di,ei
The constraints are
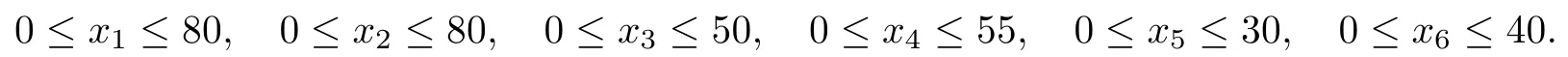
For the first player and the third player,there is a additional constraint:

Table 4.3 shows our corresponding numerical results.
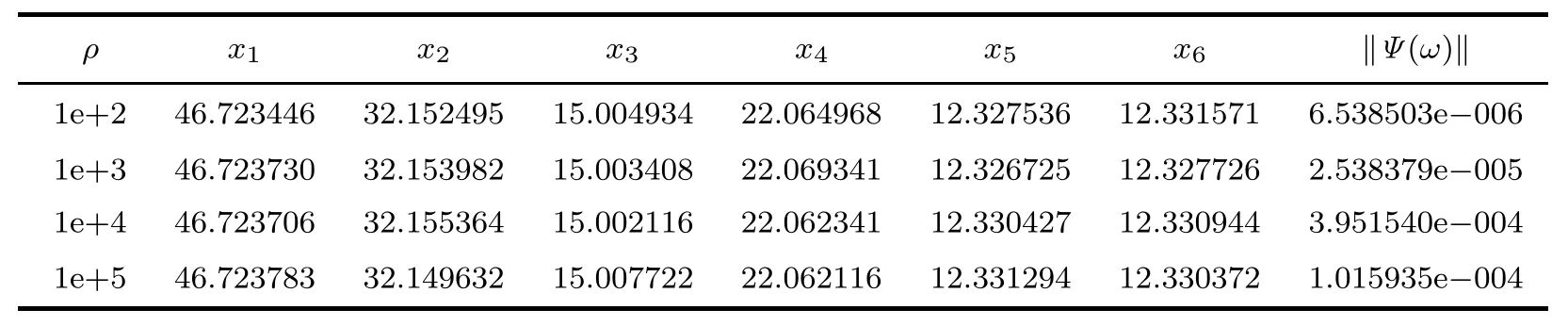
Table 4.3 Numerical results for Example 4.2
The numerical experiments show that the method proposed in this paper is implementable and e ff ective.
[1]Arrow K J,Debreu G.Existence of an equilibrium for a competitive economy.Econometrica, 1954,22:265–290.
[2]Altman E,Wynter L.Equilibrium games,and pricing in transportation and telecommunication networks.Netw.Spat.Econ.,2004,4:7–21.
[3]Hu X,Ralph D.Using EPECs to model bilevel games in restructured electricity morkets with locational prices.Oper.Res.,2007,55:809–827.
[4]Krawczyk J B.Coupled constraint Nash equilibria in enviromental games.Resour.Energy Econ.,2005,27:157–181.
[5]Facchinei F,Pang J S.Finite-Dimensional Variational Inequalities and Complementarity Problems.vol I.New York:Springer,2003.
[6]Facchinei F,Pang J S.Finite-Dimensional Variational Inequalities and Complementarity Problems.vol II.New York:Springer,2003.
[7]Harker P T.Generalized Nash games and quasivariational inequalities.European J.Oper.Res., 1991,54:81–94.
[8]Facchinei F,Fisher A,Piccialli V.On generalized Nash games and variational inequalities.Oper.Res.Lett.,2007,35:159–164.
[9]Fukushima M,Pang J S.Quasi-variational inequalities,generalized Nash equilibria,and multileader-follower games.Comput.Manag.Sci.,2005,2:21–56.
[10]Facchinei F,Pang J S.Exact penalty functions for generalized Nash problems.Large-scale Nonlinear Optim.,2006,83:115–126.
[11]Fukushima M.Restricted generalized Nash equilibria and controlled penalty algorithm.Comput.Manag.Sci.,2011,8:201–218.
[12]Facchinei F,Kanzow C.Penalty methods for the solution of generalized Nash equilibrium problems(with complete test problems).Technical Report,Institute of Mathematics.Germany: University of Wrzburg,2009.
[13]Qi L.A convergence analysis of some algorithms for solving nonsmooth equations.Math.Oper. Res.,1993,18:227–244.
[14]Clarke F H.Optimization and Nonsmooth Analysis.New York:John Wiley,1983.
[15]Mifflin R.Semismooth and semiconvex functions in constrained optimization.SIAM J.Control Optim.,1977,15:959–972.
[16]Qi L,Sun J.A nonsmooth version of Newton’s method.Math.Programming,1993,58:353–368.
[17]Rockafellar R T,Wets R J.Variational Analysis.New York:Springer,1998.
[18]Luca T D,Facchinei F,Kanzow C.A semismooth equation approach to the solution of nonlinear complementarity problems.Math.Programming,1996,75:407–439.
[19]Contreras J,Klusch M,Krawczyk J B.Numerical solutions to Nash-Cournot eqilibria in coupled constraint electricity markeds.IEEE Trans.Power Systems,2004,19:195–206.
Communicated by Li Yong
90C30,91A10,91A80
A
1674-5647(2012)02-0181-12
date:March 27,2011.
 Communications in Mathematical Research2012年2期
Communications in Mathematical Research2012年2期
- Communications in Mathematical Research的其它文章
- Computing Numerical Singular Points of Plane Algebraic Curves?
- Likely Limit Sets of a Class of p-order Feigenbaum’s Maps?
- Stability of Global Solution to Boltzmann-Enskog Equationwith External Force?
- Analysis of Bifurcation and Stability on Solutions of a Lotka-Volterra Ecological System with Cubic Functional Responses and Di ff usion?
- Stability of Fredholm Integral Equation of the First Kind in Reproducing Kernel Space?
- Trivariate Polynomial Natural Spline for 3D Scattered Data Hermit Interpolation?
