Flexural behaviors of double-reinforced ECC beams
Yan Yuan Xu Yun Wang Xun Pan Jinlong
(Key Laboratory of Concrete and Pre-Stressed Concrete Structures of Ministry of Education, Southeast University, Nanjing 210096, China)
Nowadays, concrete is the most widely used building material, which has the maturest construction technology and an irreplaceable role in building modern infrastructures. However, conventional concrete is a kind of brittle cementitious material with low tensile strength and crack resistance, limited deformability and bad impact resistance, leading to limitations for its further applications in the future[1]. Since the 1970s, fiber reinforced concrete (FRC) with high performance in strength, durability, and fluidity has become a major developing trend for the requirements of tall buildings and long-span bridges. However, the FRC still shows tensile softening after the peak tensile strength is reached. For further improving the durability and the seismic resistance of structures, fiber reinforced cementitious materials with super-high ductility have gradually become a new popular area in recent years.
In 1992, Li and Leung[2]proposed a design method for a kind of engineered cementitious composites (ECC) based on micromechanics. ECC is a cementitious material with a fiber volume fraction of 2%, and shows strain-hardening behavior under uniaxial tension accompanied with fine cracks (smaller than 60 μm). ECC has been developed for applications in the construction industry[3-5]. For properly designed ECC material, it has very good ductility with the ultimate tensile strain of more than 3%, which is nearly more than 300 times the initial cracking strain of normal concrete[6]. When concrete is fully or partially substituted by ECC in the concrete structures, deformability, durability[7]and seismic resistance can be significantly increased, which has been demonstrated by many research works. Moreover, super high deformability of ECC can also contribute to the bond strength between ECC and steel reinforcement. When the steel reinforcement reaches yielding strength, cracks in ECC can be well controlled in size and ECC can continue to bear load, resulting in increased stiffness and load bearing capacity for the structure. Also, the high shear strength of ECC can significantly reduce the use of stirrups in structural elements. Consequently, steel can be saved and the construction process becomes easier. Meanwhile, ECC maintains a great energy absorption capacity. When it is applied to some key parts of structures, not only seismic collapse can be avoided, but also crack widths after the earthquake will be reduced, which considerably reduces the repair cost of the damaged structures[8]. Therefore, the application of ECC in structural members not only can improve the ductility of structures, but also can effectively control crack width and propagation. As a result, the durability of structures can be improved. In this paper, based on the design theory of the reinforced concrete structure, theoretical studies are conducted on the flexural properties of double-reinforced ECC beams. As evident differences exist between the mechanical behaviors of ECC and normal concrete, the double-reinforced ECC beams have distinctly different deformation and mechanical characteristics from the normal RC beams, such as the stress distribution in the tension and compression zones. The load capacities for different loading stages are derived. To demonstrate the validity of the proposed calculation methods, experimental study on a double-reinforced beam is carried out. Finally, parametric studies are conducted to study the effects of the material properties of ECC and the steel reinforcement ratio on the flexural behaviors of beams.
1 Basic Assumptions
According to the Chinese code for the design of concrete structures (GB 50010—2010), the following assumptions are acceptable for analyzing the flexural behaviors of double-reinforced ECC flexural members.
1) The cross section of the ECC beam remains plane under external loading.
2) There is no relative sliding between the steel reinforcement and the ECC material.
3) The tensile strength of ECC is fully considered.
4) A bilinear constitutive model is used to describe the stress-strain behavior of ECC[9](see Fig.1), whereσtcandεtcare the initial cracking strength and strain of ECC in tension;σtuandεtuare the ultimate strength and strain of ECC in tension;σccandεccare the initial cracking strength and strain of ECC in compression;σcuandεcuare the ultimate strength and strain of ECC in compression.
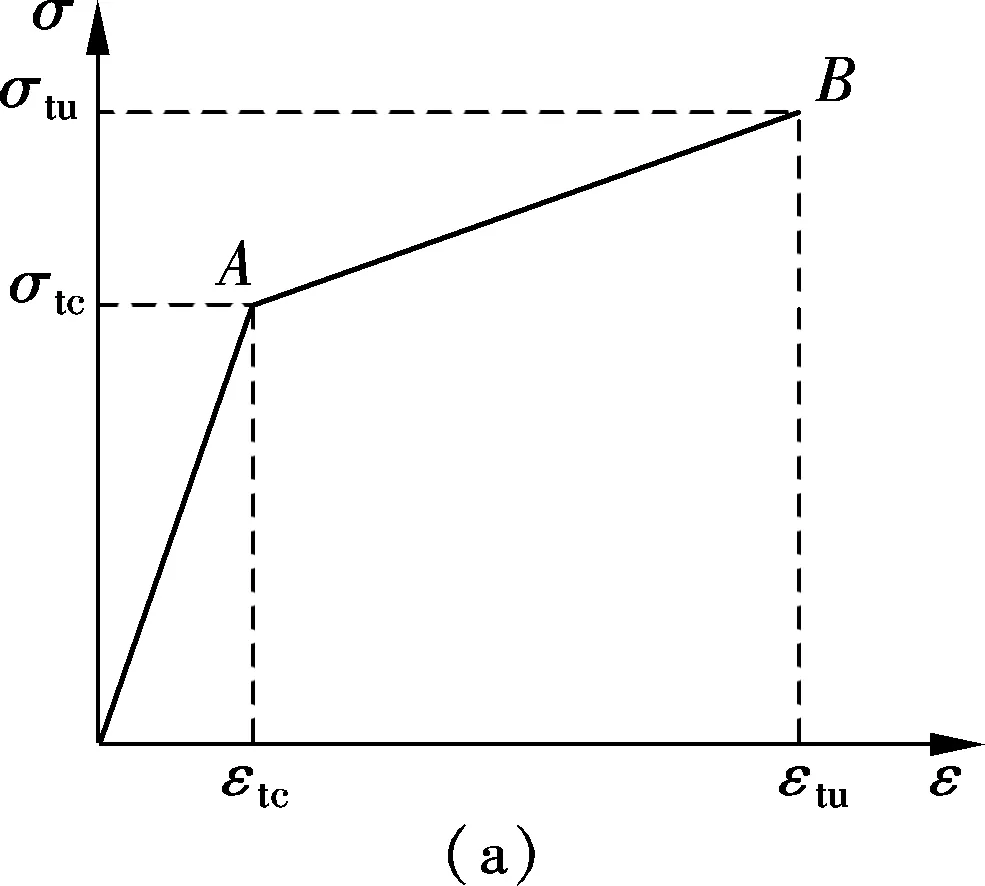
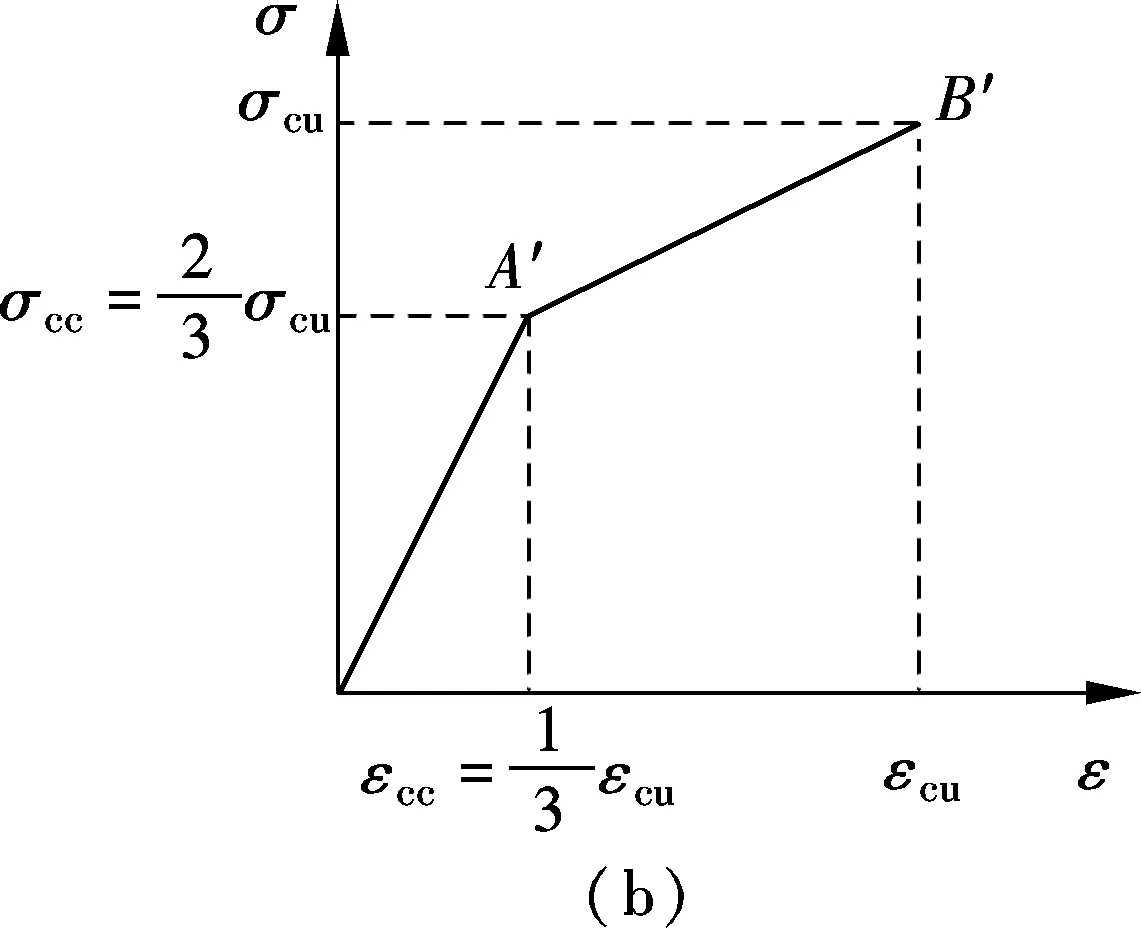
Fig.1Stress-strain relationship for ECC material. (a) In tension; (b) In compression
5) An ideal elastoplastic stress-strain relationship is assumed for the steel reinforcement (see Fig.2).
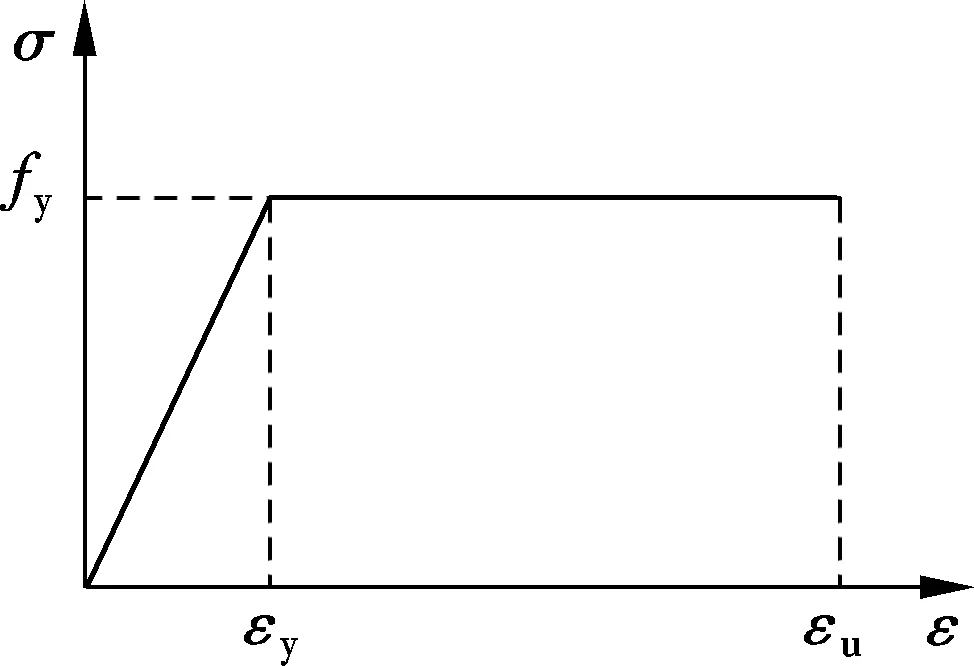
Fig.2 Stress-strain relationship of steel reinforcement
2 Theoretical Analysis of Double-Reinforced ECC Beam
The loading process for the reinforced ECC beam can be divided into three stages, i.e., the elastic stage, the cracking stage and the ultimate failure stage.
2.1 Elastic stage
When the external moment is small, there are no cracks in the tension side. Assuming that all the materials are in the elastic stage, stresses and strains in ECC are linearly distributed along the cross section. And the stress of the steel reinforcement remains at a low level. Therefore, the moment-curvature relationship is an approximate straight line in this stage. Fig.3 shows the stress and strain distributions of the ECC beam in this stage. The stresses along the cross section can be given by
(1)
whereεtis the tensile strain of the most outside fiber of the beam;ε(x) andσ(x) are the strain and stress for an arbitrary point on the beam, respectively;cis the height of the central axis of the section.
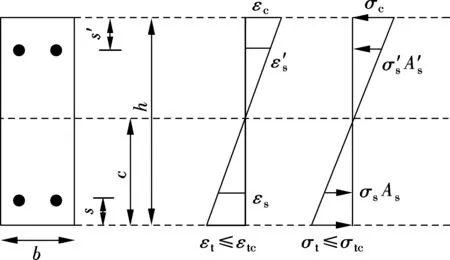
Fig.3 Stress and strain distributions of ECC beam in elastic stage
2.2 Cracking stage
At the end of this stage, the most outside fiber of the beam reaches the initial cracking strain of ECC, and the beam starts to enter the second stage, i.e., the cracking stage. When the external moment is relatively small, the maximum compressive strain in ECC is lower thanεcc, so the compression zone is still in the elastic stage. With the increase in the external moment, the maximum compressive strain in ECC is greater thanεcc, and the compression zone enters the plastic stage.
Fig.4 shows the stress and strain distributions of the ECC beam when the compression zone is still in the elastic stage. The stresses along the cross section are given by
(2)
whereais the height of the tensile plastic zone.
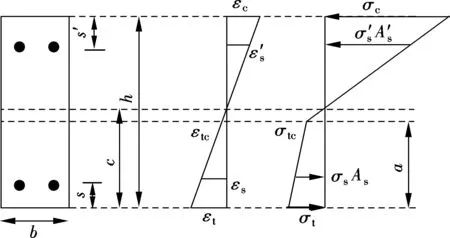
Fig.4 Stress and strain distributions of ECC beam in cracking stage with a linear stress distribution in compression zone
With the increase in the external moment, the maximum compressive strain of ECC in the compression zone is greater thanεcc, and the compression zone starts to enter the plastic stage. Fig.5 shows the stress and strain distributions of the ECC beam in this stage. The stresses along the cross section are given by whereeis the height of the compressive plastic zone from the bottom of the beam.
(3)
In this stage, when the most outside fiber of the compression zone reaches the ultimate compression strain, the beam is considered to fail due to the compression failure of ECC. For this failure mode, ECC in the compression zone reaches its ultimate compression strain before the tensile steel reinforcement reaches its yielding strain.
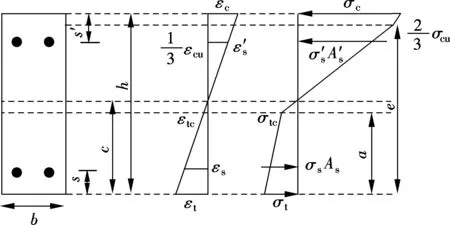
Fig.5 Stress and strain distributions of ECC beam in cracking stage with a bilinear stress distribution in compression zone
2.3 Ultimate failure stage
With the further increase in the external moment, the tensile steel reinforcement enters the yielding stage, and the cross section starts to get into the third stage, i.e. the ultimate failure stage. There are three different strain distributions of ECC and steel reinforcement, which are given as follows:
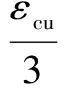
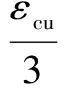
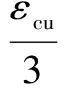
Through the above analyses on different stages of the steel double-reinforced ECC beam, the moment-curvature curve can be obtained.
3 Experimental Verification of Theoretical Model
In this paper, the test results of a double-reinforced ECC beam are compared with the theoretical calculation results to verify the validity of the derived equations.
3.1 Introduction of experiments
A four-point bending test is carried out to study the flexural behavior of the double reinforced ECC beam. During the test, three linear variable differential transformers (LVDTs) are used to record data of the deflections in the midspan. Along the depth of the middle of the beam, three strain gauges are attached with 35, 150 and 265 mm from the bottom of the beam. They are used to analyze the strain distributions during the loading process. Other three strain gauges are attached to the tensile steel reinforcement with 40, 80 and 120 mm from the midspan for recording strains of the steel reinforcement. A hydraulic jack is used to apply load on the beam, and the force from the hydraulic jack is recorded by a pressure sensor. The test beam is loaded to failure (i.e., the residual load was lower than 80% of the peak load) before unloaded. Fig.6 shows the specimen dimension information and arrangement of the instruments. The length of the beam is 2 350 mm, and the section is 200 mm in width and 300 mm in depth. According to the test results of material properties, the initial cracking strain and strength of ECC are 0.21 Pa and 3 MPa; the ultimate tension and compression strain are 0.03 and 0.004, and the corresponding stresses are 4.5 and 35 MPa, respectively. The elastic modulus and yielding strength of the steel reinforcement are 200 GPa and 460 MPa, respectively.
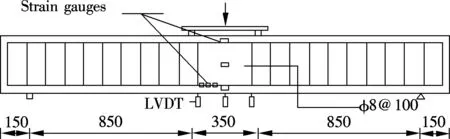
Fig.6 Dimensions of beam and loading configurations (unit: mm)
3.2 Comparisons between test and theoretical results
Fig.7 shows the moment-tensile steel reinforcement strain curves and moment-curvature curves from experimental and theoretical calculations. According to the comparisons, the moment-tensile steel reinforcement strain curve from the theoretical calculation shows good consistency with the test results. The theoretical yielding moment is 82.78 kN· m, which is only 3.8% higher than the test result 79.77 kN· m. The theoretical moment-curvature curve also shows good consistency with the test result. Especially when the curvature is less than 3.09×10-5mm-1, the theoretical yielding curvatureφyis 1.66×10-5mm-1which is only 5% less than the test result. However, after the curvature reaches 3.09×10-5mm-1, due to the faster development of cracks, stiffness of the beam starts to degrade, leading to deviation of the theoretical results from the test results. Finally, the theoretical ultimate bearing capacity is 88.32 kN· m, which is 7.8% higher than that of the test result (81.90 kN· m). And the theoretical curvature is 3.66×10-5mm-1, which is smaller than the test result (4.84×10-5mm-1). Overall, the calculation curves of moment-tensile steel reinforcement strain and moment-curvature are in good consistency with the test results.
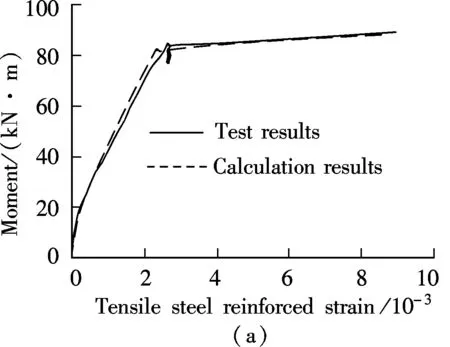
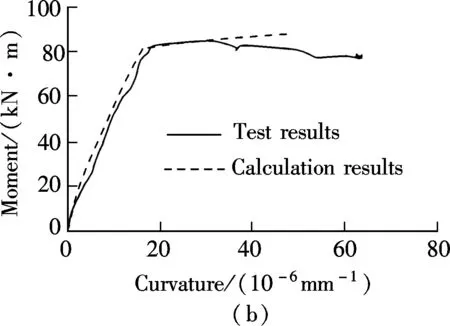
Fig.7 Comparison of calculation and test. (a) Moment-tensile steel reinforced strain curves; (b) Moment-curvature curves
4 Parametric Studies
Based on the parameters of the test, parametric studies are conducted for discussing the effects of the compression strength, ultimate compression strain, tension strength of ECC and the steel reinforcement ratioρ. The effects of these parameters on the ductility, ultimate curvatureφuand ultimate bearing capacityMuof reinforced ECC beams are shown in Tab.1.
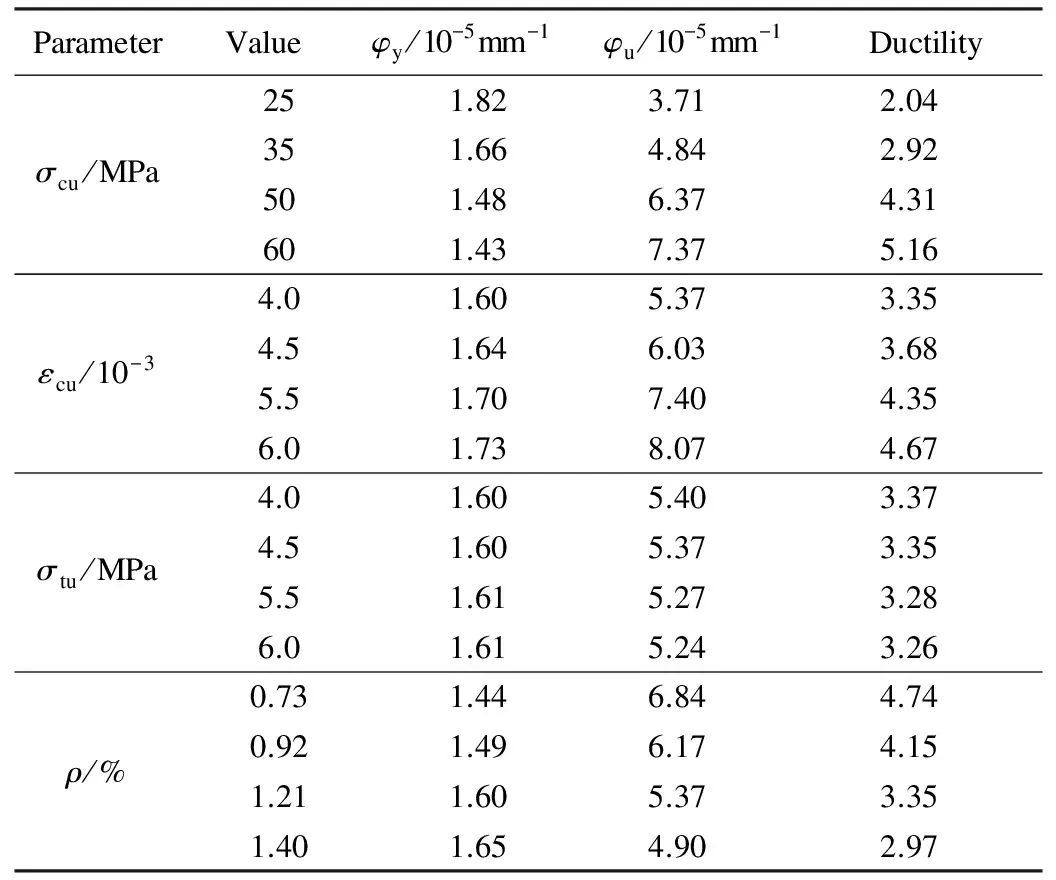
Tab.1 Parameters and corresponding ductility
4.1 Effects of ultimate compression strength and strain of ECC material
The correlation curves of Figs.8 to 11 show how the ultimate compression strength and the ultimate compression strain of ECC influence the ultimate bearing capacity and the ultimate curvature of the cross section. According to Fig.8 and Fig.9, both the ultimate curvature and the ultimate bearing capacity increase with the ultimate compression strength of ECC. When the ultimate compression strength increases from 25 to 60 MPa, the corresponding curvature doubles, and the ductility of the reinforced ECC beam shows an increase of 150%. Meanwhile, the ultimate bearing capacity increases only 16%. Therefore, the ultimate compression strength of ECC material plays an important role in the flexural performance of the ECC beams.
As shown in Fig.10 and 11, both the ultimate curvature and the ultimate bearing capacity linearly increase with the ultimate compression strain of ECC. With the ultimate compression strain increasing from 0.004 to 0.006, the ultimate curvature shows an increase of approximately 50% and the ductility an increase of 40%. However, the ultimate bearing capacity improves only about 1%. Because the height of the central axis remains at 225 mm from the bottom of the beam, the ultimate curvature increases linearly with the ultimate compression strain.
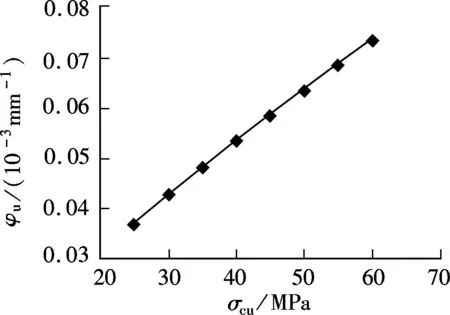
Fig.8 σcu vs. φu
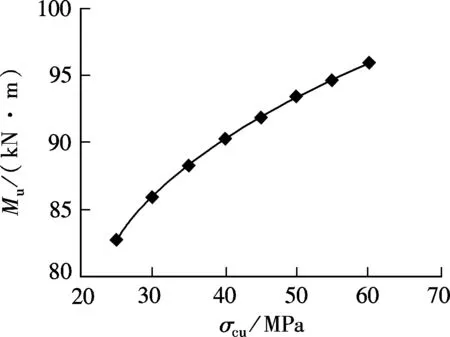
Fig.9 σcu vs. Mu
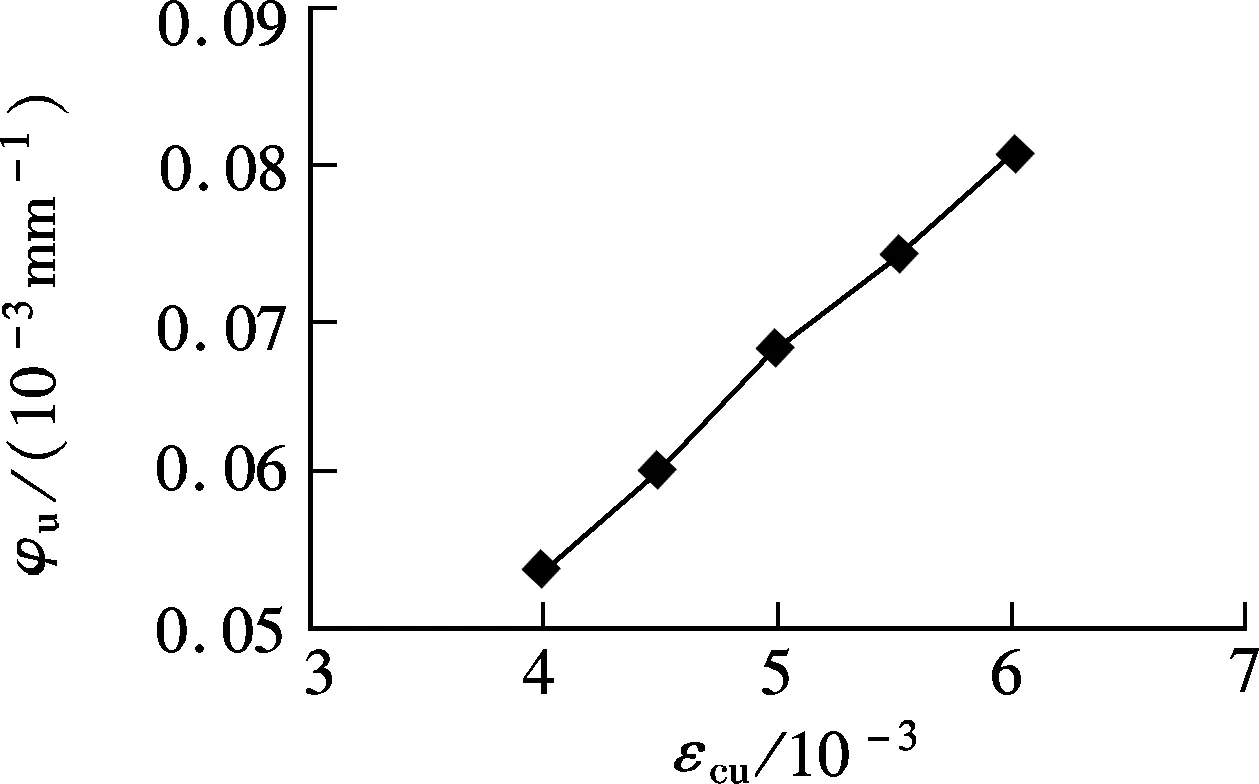
Fig.10 εcu vs. φu
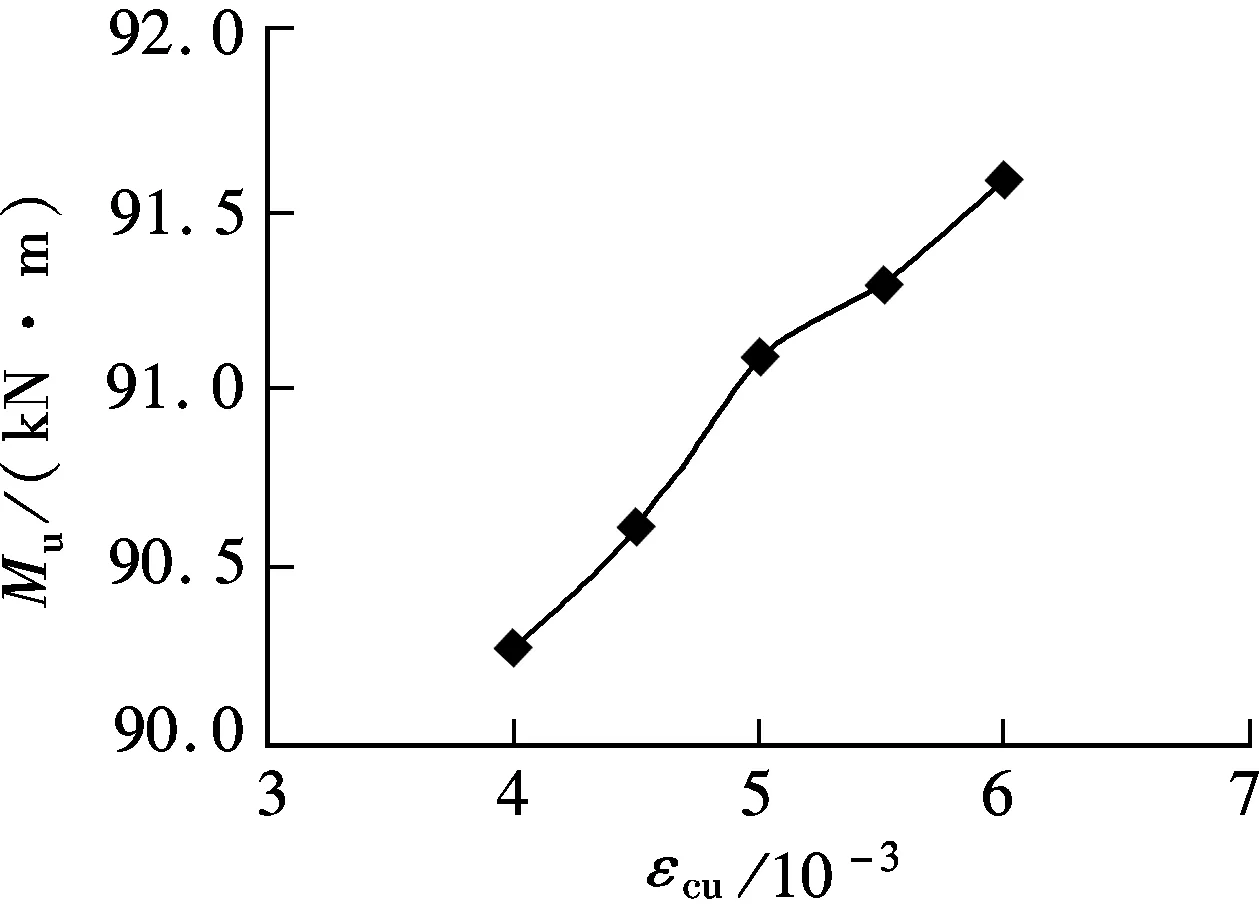
Fig.11 εcu vs. Mu
4.2 Effects of ultimate tension strength of ECC material
Fig.12 and 13 show the correlations ofφuvs.σtuandMuvs.σtu, respectively. It is shown that the ultimate curvature and ductility degrade as the tensile strength of ECC material increases. However, the corresponding load bearing capacity increases with the tensile strength of ECC. In a word, the ultimate curvature and the bearing capacity are affected slightly with the increase in the ultimate tensile strength of ECC from 4 to 6 MPa. Within nd the bearing capacity are affected slightly
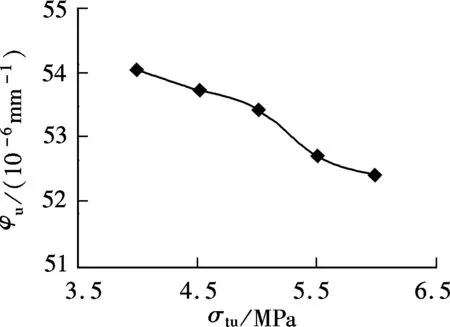
Fig.12 φu vs. σtu
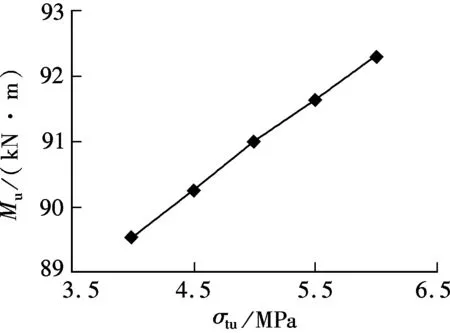
Fig.13 Mu vs. σtu
4.3 Effects of steel reinforcement ratio of beams
Figs.14 and 15 show the correlation curves ofρvs.φuandρvs.Mu, respectively. As the steel reinforcement ratio becomes higher, the height of the central axis becomes smaller, so does the magnitude of curvature. Fig.15 shows that the ultimate bearing capacity increases with the steel reinforcement ratio, but the height of the central axis degrades with it. In the compression zone, because both the force and the force arm increase, the ultimate bearing capacity improves significantly. Therefore, the increase in the reinforcement ratio can improve the ultimate bearing capacity of beams to some extent, but it will lead to degradation of ductility at the same time.
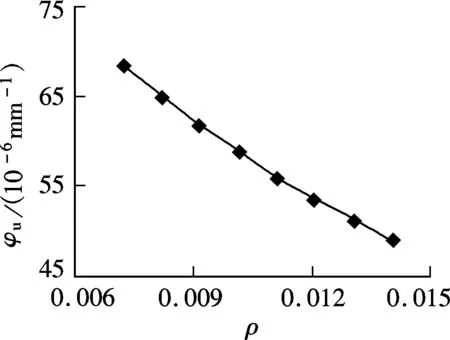
Fig.14 φu vs. ρ

Fig.15 Mu vs. ρ
5 Conclusion
This paper focuses on theoretical and experimental research on the flexural behaviors of double-reinforced ECC beams. Based on the assumption of the plane section remaining plane in bending and simplified constitutive models of materials, calculation methods of the load carrying capacities for different critical stages are proposed. Also, these calculation methods are demonstrated by comparing the test results with the calculation results. Finally, parametric studies on compression strength, ultimate compression strain, tension strength of ECC material and the steel reinforcement ratio are conducted. The results show that the increase in the compression strength of ECC will greatly improve the load bearing capacity, curvature and ductility of beams. The increase in the ultimate compression strain can significantly improve the ultimate curvature and ductility, but it has little effect on the load bearing capacity of beams. The tensile strength of ECC has little effect on the flexural behaviors of ECC beams. The increase in the steel reinforcement ratio can lead to a significant improvement of the load bearing capacity and stiffness of beams, but degradation of the ductility of beams.
[1]Li Zongjin.Advancedconcretetechnology[M]. New Jersey: John Wiley & Sons, 2011:13-14.
[2]Li V C, Leung C K Y. Steady state and multiple cracking of short random fiber composites [J].ASCEJournalofEngineeringMechanics, 1992,188(11):2246-2264.
[3]Kim Y Y, Fischer G, Li V C. Performance of bridge deck link slabs designed with ductile engineered cementitious composite [J].ACIStructuralJournal, 2004,101(6): 792-801.
[4]Lepech M D, Li V C. Application of ECC for bridge deck link slabs [J].MaterialsandStructures, 2009,42(9): 1185-1195.
[5]Lepech M D, Li V C. Sustainable pavement overlays using engineered cementitious composites [J].InternationalJournalofPavementResearchandTechnology, 2010,3(5): 241-250.
[6]Christopher K Y L, CheungY N, Zhang J. Fatigue enhancement of concrete beam with ECC layer [J].CementandConcreteResearch, 2007,29(6):465-473.
[7]Kesner K, Billington S L. Investigation of infill panels made from engineered cementitious composites for seismic strengthening and retrofit [J].ASCEJournalofStructuralEngineering, 2005,131(11):1712-1720.
[8]Billington S L. Damage-tolerant cement based materials for performance based earthquake engineering design: research needs[C]//ProceedingsoftheFifthInternationalConferenceonFractureMechanicsofConcreteandConcreteStructures. Vail, Colorado, USA, 2004:53-60.
[9]Maalej M, Li V C. Flexural/tensile-strength ratio in engineered cementitious composites [J].JournalofMaterialsinCivilEngineering, 1994,6(4):513-528.
 Journal of Southeast University(English Edition)2013年1期
Journal of Southeast University(English Edition)2013年1期
- Journal of Southeast University(English Edition)的其它文章
- Factors affecting headway regularity on bus routes
- Effects of carbonaceous conductive fillers on electrical and thermal properties of asphalt-matrix conductive composites
- Fatigue behavior of basalt-aramidand basalt-carbon hybrid fiber reinforced polymer sheets
- Effect of chloride salt concentration on unconfined compression strength of cement-treated Lianyungang soft marine clay
- Response mechanism for widened pavement structure subjected to ground differential settlement
- Flexural behaviors of double-reinforced ECC beams
