賈秀利,關(guān)麗紅,王振華

(1. 吉林工商學(xué)院 基礎(chǔ)部,長(zhǎng)春 130062;2. 長(zhǎng)春大學(xué) 理學(xué)院,長(zhǎng)春 130022;3. 吉林大學(xué) 數(shù)學(xué)研究所,長(zhǎng)春 130012)

0 引 言

考慮下列混合型隨機(jī)時(shí)滯發(fā)展方程的系數(shù)滿足局部Lipschitz條件和Khasminskii條件時(shí)解的存在唯一性:

dX(t)=AX(t)+F(X(t),X(t-τ),r(t))dt+G(X(t),X(t-τ),r(t))dW(t),x∈[0,T],

(1)

其滿足初始條件

(2)

當(dāng)隨機(jī)偏微分方程的系數(shù)滿足局部Lipschitz條件和線性增長(zhǎng)條件時(shí),方程的解存在唯一[1-5]. 但一些隨機(jī)系統(tǒng)的系數(shù)并不滿足線性增長(zhǎng)條件,例如: 對(duì)于一些隨機(jī)微分方程和隨機(jī)時(shí)滯方程,Rafail[6]和Mao等[7]分別用Khasminskii型條件替代線性增長(zhǎng)條件得到了方程解的存在唯一性;Bao等[8]研究了一類帶跳擴(kuò)散的隨機(jī)偏微方程的系數(shù)滿足局部Lipschitz條件和Khasminskii型條件時(shí)解的存在唯一性;Bao等[9]研究了混合型隨機(jī)熱方程的Lyapunov指數(shù). 本文研究混合型隨機(jī)時(shí)滯偏微分方程解的存在唯一性,并用實(shí)例驗(yàn)證了理論結(jié)果.

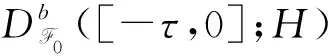
E〈W(t),x〉〈W(s),y〉=(t∧s)〈Q1/2x,Q1/2y〉K, ?x,y∈K,

其中Q是K上的正自伴跡算子[2]. 令R+∶=[0,∞),N是正整數(shù). 再令{r(t),t∈R+}是在概率空間(Ω,Ft,{Ft}t≥0,P)上取值于有限狀態(tài)空間S∶={1,2,…,N}內(nèi)的右連續(xù)Markov鏈,它的生成元Γ∶=(γij)N×N為

1 主要結(jié)果

假設(shè)：

(H1)A是C0半群T(t)(t>0)的無(wú)窮小生成元,并且是一個(gè)無(wú)界算子;

(H2) 映射F:H×H×S →H,G:H×H×S → L(H,K)是Borel可測(cè)的,并且滿足局部Lipschitz 條件,即對(duì)于每個(gè)h>0,都存在一個(gè)常數(shù)Lh>0,使得對(duì)于所有的x1,x2,y1,y2∈H及‖xi‖H∨‖yi‖H≤h(i=1,2),有

定義1如果下列條件成立,則隨機(jī)過(guò)程{X(t),t∈[0,T]}(0≤T≤∞)稱為方程(1)的解:

1)X(t)是Ft適應(yīng)的,并且當(dāng)t≥0時(shí),以概率1有Cdlg路徑;

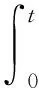
以概率1成立.

1)U(x,i)關(guān)于x是二次(Fréchet)可微的;

2)Ux(x,i)和Uxx(x,i)分別在空間H和L(H,H)上連續(xù).

引理1假設(shè)U∈C2(H;R+),{X(t),t≥0}是方程(1)的解,則當(dāng)t≥0時(shí),

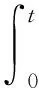
其中: ?x,y∈H,i∈S;算子

定理1假設(shè)(H1),(H2)成立,并且下列Khasminskii型條件成立: 假設(shè)存在一個(gè)函數(shù)U∈C2(H×S;R+)及一個(gè)正常數(shù)l,使得

LU(x,y,i)≤l(1+U(x)+U(y)), (x,y)∈H×H,

并且

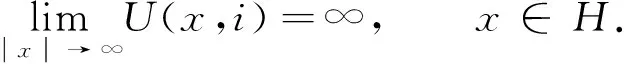
證明: 由于方程(1)的系數(shù)關(guān)于(x,y,i)滿足局部Lipschitz條件,所以方程(1)在極大區(qū)間t∈[-τ,σ∞)內(nèi)存在唯一的局部解x(t),其中σ∞是爆破時(shí)間. 則只需證明σ∞=∞. 對(duì)任意的正數(shù)k≥1,定義停時(shí)τk=σ∞∧inf{t∈[0,τ∞): |x(t)|≥k}. 蘊(yùn)含著τk隨k增加.

利用標(biāo)準(zhǔn)截?cái)嗉夹g(shù)[10],定義

對(duì)于x,y∈H,r∈S,Fk(x,y,r),Gk(x,y,r)是全局Lipschitz的,則下述隨機(jī)偏微分方程在區(qū)間[-τ,τk)內(nèi)存在唯一解:

dXk(t)=AXk(t)+Fk(Xk(t),Xk(t-τ),r(t))dt+Gk(Xk(t),Xk(t-τ),r(t))dW(t),t∈[0,T],

(3)

且滿足初始條件:

(4)

由Khasminskii型條件,可得

其中

由Gronwall不等式,可得

EU(Xk(t∧τk))≤(C+lt)e2lt.

進(jìn)一步,有

P(τk≤t)≤E(U(Xk(τk)Iτk≤t)≤(C+lt)e2lt.

則

令k→ ∞,可得 P(τ≤t)=0. 由t的任意性,可得 P(τ=∞)=1. 證畢.

例1考慮帶擴(kuò)散的隨機(jī)時(shí)滯偏微分方程:

(5)

對(duì)于所有的(x,y,i)∈H×H×S,令

并且

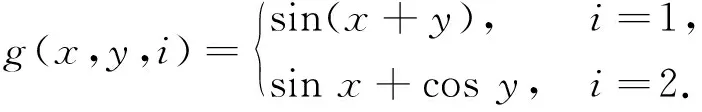
再令

則

其中l(wèi)是一個(gè)常數(shù). 則由定理1知,方程(5)存在唯一全局解.

[1] CHOW Pao-liu. Stochastic Partial Differential Equations [M]. Boca Raton: Chapman and Hall/CRC,2007.

[2] Prato G,Da,Zabczyk J. Stochastic Equations in Infinite Dimensions [M]. Cambridge: Cambridge University Press,1992.

[3] LIU Kai. Stability of Infinite Dimensional Stochastic Differential Equations with Applications [M]. Boca Raton: Chapman and Hall/CRC,2005.

[4] Peszat S,Zabczyk J. Stochastic Partial Differential Equations with Lévy Noise: An Evolution Equation Approach [M]. Cambridge: Cambridge University Press,2007.

[5] Claudia P,Michael R. A Concise Course on Stochastic Partial Differential Equations [M]. Berlin: Springer,2007.

[6] Rafail K. Stochastic Stability of Differential Equations [M]. Aeidelberg: Springer,1980.

[7] MAO Xue-rong,Rassias M J. Khasminskii-Type Theorems for Stochastic Differential Delay Equations [J]. Stoch Anal Appl,2005,23: 1045-1069.

[8] BAO Jian-hai,Truman A,YUAN Cheng-gui. Almost Sure Asymptotic Stability of Stochastic Partial Differential Equations with Jumps [J]. SIAM J Control Optim,2011,49(2): 771-787.

[9] BAO Jian-hai,MAO Xue-rong,YUAN Cheng-gui. Lyapunov Exponents of Hybrid Stochastic Heat Equations [J]. Systems Control Lett,2012,61(1): 165-172.

[10] Friedman A. Stochastic Differential Equations and Applications [M]. 2nd ed. Dover: Dover Pulications,2006.