YU Dan(于丹)and YANG Jun-Zhong(楊俊忠)

School of Science,Beijing University of Posts and Telecommunications,Beijing 100876,China

1 Introduction

Synchronization,an emergent property in systems consisting of a large number of elementary unites with their own dynamics,is ubiquitous in physical systems,chemical systems,social systems,and biological systems.[1?7]A powerful approach on analyzing synchronization in these systems is to model elementary units as phase oscillators when the interaction among them is weak.Along this line,the Kuramoto model is the most representative one.[7?9]The original Kuramoto model assumes that the phase oscillators are coupled globally and their natural frequencies follow a given distribution.The theoretical analysis shows that there exists a critical coupling strength above which the coupled phase oscillators transit from an incoherent state to a partial synchronous state.Further increasing the coupling strength may eventually lead to a global synchronization in which all phase oscillators rotate with a common frequency.

Recently,the Kuramoto model on complex networks in which each phase oscillator only interacts with its nearest neighbors has drawn great attentions.[10]It has been found that the topological properties of complex networks have strong impacts on the critical coupling strength for the onset of synchronization and on the scenarios of the transition to synchronization.[11?14]Nevertheless,the synchronization transitions on diあerent networks are always continuous one(or the second order ones).

It is a well-known fact that the roles of an elementary unit on collective dynamics in coupled systems depend not only on its own dynamical characteristics but also on its position on the network.[15]Recently,motivated by the abrupt percolation transition on complex networks,[16?18]Garde?nes et al.introduced a microscopic correlation between the structural and the dynamical properties of the system[19]by setting the natural frequency of a phase oscillator to be the degree of the node it sits on.They found an explosive synchronization in which the synchronization transition becomes a discontinuous one(or a f i rst-order transition)and the incoherent state may coexist with the global synchronization in a certain range of the coupling strength.Furthermore,the explosive synchronization on scale-free networks is also found when phase oscillators are replaced by chaotic R¨ossler oscillators.[20]However,how the explosive synchronization depends on the correlation between the structural and the dynamical properties of the system is still an open problem,which is the goal in this work.

In this work,we f i rst consider the frequency distribution following the degree distribution of networks.We introduce a correlation factor β accounting for the correlation between the structural and the dynamical properties of the system.Then we show that the critical coupling strength has strong dependence on the correlation factor β and that the transition to synchronization may be either the second-order or the f i rst-order one depending on the correlation factor β.For proper β,we f i nd that the explosive synchronization transition may occur between the incoherent state and partially synchronized states.Finally,we show that the dependence of the synchronization transition on the correlation factor can also be found when the natural frequency follows other types of distributions such as a Lorentzian probability distribution.

2 Model

Let us consider a network of N coupled phase oscillators.Each phase oscillator is characterized by a phase θ(t).The motion equation of the systems is given by the Kuramoto model:[7]

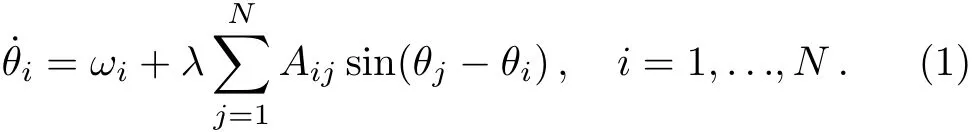
ωiis the natural frequency of the oscillator i and is taken from a probability distribution g(ω).λ stands for the coupling strength among oscillators.Aijare the elements of an N×N adjacency matrix A,so that Aij=1 when the oscillators i and j are connected while Aij=0 otherwise.Aijgives rise to the degree kiof the node the oscillator i sits on.In this work,we consider scale-free networks whose degree distribution P(k)follows a power law.

To introduce the correlation factor β,we assume that phase oscillators have sit on networks but with unknown natural frequencies.We f i rst sort the phase oscillators by the degrees of the nodes they sit on and have a structural sequence{k1,k2,...,kN}in which k1≥ k2≥ ···≥ kN.In this notation,the label kidenotes the i-th phase oscillator,which has the degree ki.Then we sort the natural frequencies to be assigned and have a dynamical sequence{ω1,ω2,...,ωN}in which ω1≤ ω2≤ ···≤ ωN.In this notation,the label ωidenotes the i-th natural frequency.For the case that g(ω)has the same form as P(k),the relation between two sequences lies at ωi=kN?i+1.To be stressed,the numbers in the subscript of ωiare just for index and are not related to phase oscillators.

To establish the correlation between the structural and the dynamical properties in the model,we introduce the correlation factor β (β ∈ [1,N])as follows.The natural frequency ω1is assigned to the β-th oscillator in the structural sequence.Then,the natural frequency ω2is assigned to the(β+1)-th oscillator with the probability(N ? β)/(N?1)or to the(β ?1)-th oscillator otherwise.By repeating the above procedure,every phase oscillator in the structural sequence will be assigned a natural frequency in the dynamical sequence.We call the system with the correlation factor β=N the one with positive correlation between the structural and the dynamical properties,which is the case in the work by Garde?nes et al.[19]Correspondingly,we call the system with β=1 the one with negative correlation.With the increase of β,more and more phase oscillators with higher degrees acquire large natural frequencies,which changes the correlation between the topological and the dynamical properties in the model.Therefore,we may build up arbitrary intermediate correlation between positive and negative ones through this way.

In the rest of work,we will see that the correlation between the structural and the dynamical properties has strong impacts on the critical coupling strengthes such as λffor the onset of synchronization and λbfor the oあset of synchronization.Moreover,we will f i nd that the correlation factor might aあect the type of the synchronization transition.

3 Results and Analysis

We simulate the Kuramoto model on Barab′asi–Albert(BA)networks[21?22]by using the fourth order Runge–Kutta algorithm.The size of the network is N=5000 and the mean degree 〈k〉=6.

To investigate the transition to synchronization in the system of Eq.(1),we consider the complex order parameter,which is def i ned as

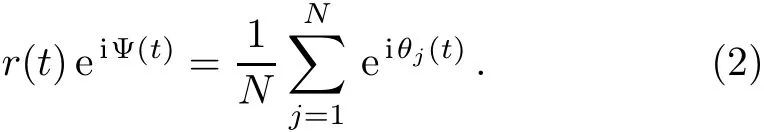
Ψ(t)is the average phase of the collective dynamics of the system and the modulus r(t)∈[0,1]represents the degree of synchronization among oscillators.r=1 when all oscillators get synchronized to Ψ(t).On the other hand,r=0 indicates the incoherent state where the phases of oscillators are evenly distributed in[0,2π].In simulations,for a given λ,the modulus of the order parameter is averaged over a long time interval after transient.

To explore the synchronization transition,we compute two synchronization diagrams r(λ),labelled as the forward and the backward continuations,for diあerent β.Figure 1(a)shows the results for β=1 the case with negative correlation between the topological and the dynamical properties.From the f i gure,it is clear that both the forward continuation diagram and the backward continuation diagram give rise to the same dependence of r on λ,which refers to a continuous synchronization transition.Several features in the f i gure should be addressed.Firstly,the modulus of the order parameter r has a much high value even when the coupling is extremely weak.The feature is related to the distribution of the natural frequency,which only allows a few of diあerent values and a large amount of oscillators such as those with the lowest natural frequency have already formed synchronous clusters accidently.In this situation,we treat the onset of synchronization as an event that oscillators with diあerent natural frequencies get trapped and,consequently,the critical coupling strength is identif i ed by the discontinuity in the slope of r(λ)(Here,the onset of synchronization lies at around λ ? 0.2).The second feature in Fig.1(a)is that the increase of r with λ is not in a smooth way after the onset of synchronization and there exist several coupling strengthes λ at which the slope of r(λ)is not continuous.As shown below,these discontinuities account for the transitions between diあerent partially synchronized states.

However,the continuous synchronization transition can be observed only at small β.Figure 1(b)shows the results for β=800 where the forward continuation diagram shows a sharp jump from the incoherent state with r? 0 to a state with r? 0.6 at λf? 0.58 while the transition from a synchronous state back to the incoherent one occurs at λb? 0.43 in the backward continuation diagram.Further increasing β leads the discontinuous characteristics of the synchronization transition to be more clearer.As shown by Figs.1(c)and 1(d),increasing β postpones the onset of synchronization in the forward continuation diagram and the oあset of the synchronized states in the backward continuation diagram to stronger coupling strengthes and the range of the coupling strength for the coexistence of the incoherent state and the synchronous states may be widened.The results in Fig.1 show that the correlation between the structural and the dynamical properties in the model is crucial for the characteristics of the synchronization transition and the synchronization is diきcult to achieve for high correlation factor β.

To get deep insights on synchronization transition at diあerent β,we compute the eあective frequency of phase oscillators in the forward continuation of λ.For a phase oscillator i,its eあective frequency is de fi ned as ωieあ=〈θ˙i〉where 〈·〉is the time average over a long time interval after transient.The results are presented in Fig.2 in which diあerent colors are used to distinguish oscillators with diあerent degrees.Figure 2(a)shows the scenario how the continuous synchronization transition is proceeded at β =1.The transition at λ ? 0.2 is characterized by the event that part of oscillators with natural frequencies ω=4 and ω=3 get synchronized.With the increase of the coupling strength,the global synchronization among oscillators with ω =3 and with ω =4 are built gradually.After that,the partial synchronization and the global synchronization among oscillators with larger natural frequencies and those already in synchronization happen at larger coupling strength successively.The occurrence of each partial synchronization accompanies a discontinuity in the curve of r(λ)as observed in Fig.1(a).In the case of β =1,the oscillators with high degrees such as ki＞ 6 have their natural frequencies less than ω=4.

The synchronization among oscillators in Fig.2(a)actually has two-folded implications. On the one hand,the f i gure indicates that the oscillators with highest degrees get synchronized f i rstly,which is in agreement with the observations on scale-free networks[we call it network-assisted-synchronization-mechanism(NASM)].On the other hand,the f i gure indicates that the oscillators got f i rst synchronized are those whose natural frequencies are most probable,which is also in agreement with the observations in original Kuramoto model[We call it the frequency-assisted-synchronization mechanism(FASM)].To be noted,due to the power law distribution of the natural frequency,the common frequency among the synchronized oscillators is not equal to ? = 〈k〉=6 before the global synchronization among all oscillators is built up.

Increasing the correlation factor β will break up the coincidence between NASM and FASM at β=1,which may lead the type of synchronization transition to change from a continuous to a discontinuous one. As shown in Figs.2(b)–2(d),the oscillators with high degrees become more impossible to adopt probable natural frequencies with the increase of the correlation factor β.Resultantly,NASM and FASM can not be realized simultaneously,which means that oscillators with high degrees are not favored by FASM or oscillators with probable natural frequencies are not favored by NASM,and the competition between NASM and FASM leads to a discontinuous synchronization transition.In Figs.2(b)(β=800),(c)(β =3500),and(d)(β =5000),the synchronization transition becomes discontinuous and,generally,the critical coupling strength λfincreases with β.Interestingly,we f i nd that,for intermediate β,the discontinuous synchronization transition may occur between the incoherent state and a partial synchronous state for intermediate correlation factors[see Figs.2(b)and 2(c)],which is found in a second order Kuramoto model on scale-free networks recently.[23]There are still a large amount of oscillators with high natural frequencies are outside of the synchronous clusters after the onset of synchronization.Beyond λf,there exist several successive transitions between diあerent partial synchronous states(or global synchronous state)and these transitions are types of continuous ones.Figures 2(b)and 2(c)reveal another feature at the discontinuous transition between the incoherent state and a certain partial synchronous state:Right at λf,the distribution of the eあective frequency becomes narrow suddenly for oscillators outside synchronous clusters,which is not observed in a continuous synchronization transition.For positive correlation with β=N,the discontinuous synchronization transition occurs between the incoherent state and the global synchronous state in which all phase oscillators have a same eあective frequency ? = 〈k〉=6 beyond the onset of synchronization as shown in Fig.2(d).

Fig.2 (Color online)The eあective frequencies of oscillators are plotted against the coupling strength in the forward continuation diagram in Fig.1 for diあerent correlation factors β (a)β =1,(b)β =800,(c) β =3500,(d) β =5000.Diあerent colors stand for the oscillators with diあerent degrees.

The impacts of the correlation factor β on the synchronization transition can be summarized in Fig.3 where the onset of synchronization λfin the forward continuation diagram and the oあset of synchronization λbin the backward continuation diagram are presented against β.For each β,we present data for ten realizations of the correlation between the structural and the dynamical properties.Figure 3 shows that the synchronization transition is a continuous one for β ＜ 300 where λf= λbwhile a discontinuous one otherwise.From the f i gure,we f i nd that,for diあerent realizations of correlation,λfand λbf l uctuate greatly and that both λfand λbtend to go up with β when synchronization transition is a discontinuous one.Figure 3 also shows that λbreaches a saturated value earlier than λbwith the increase of β and the range of the coupling strength for the coexistence of the incoherent state and the synchronous state is enlarged with β.

In the above investigations,the probability distribution of the natural frequencies follows the degree distribution of the underlying networks,which only consists of a few of diあerent natural frequencies.However,the dependence of synchronization transition on correlation between the structural and the dynamical properties is not limited to this special distribution of natural frequencies.Here we consider a widely used distribution for natural frequencies,the Lorentzian distribution which follows g(ω)= γ/(ω2+ γ2)π. The width γ is set to be γ=0.1.The N natural frequencies are randomly drawn from the Lorentzian distribution and are sorted according to the probabilities they appear. Therefore,we have a dynamical sequence{ω1,ω2,...,ωN}such that g(ω1)≤ g(ω2)≤ ···≤ g(ωN).Then we introduce the correlation factor β and assign each oscillators with a natural frequency by following the procedure in the model section.Figure 4 shows the results of r against λ for diあerent β.Similar to Fig.1,whether the synchronization transition is a continuous one or a discontinuous one depends on the value of β.Figure 4 also shows that the critical coupling strengthes λfand λbincrease with β in an overall trend.

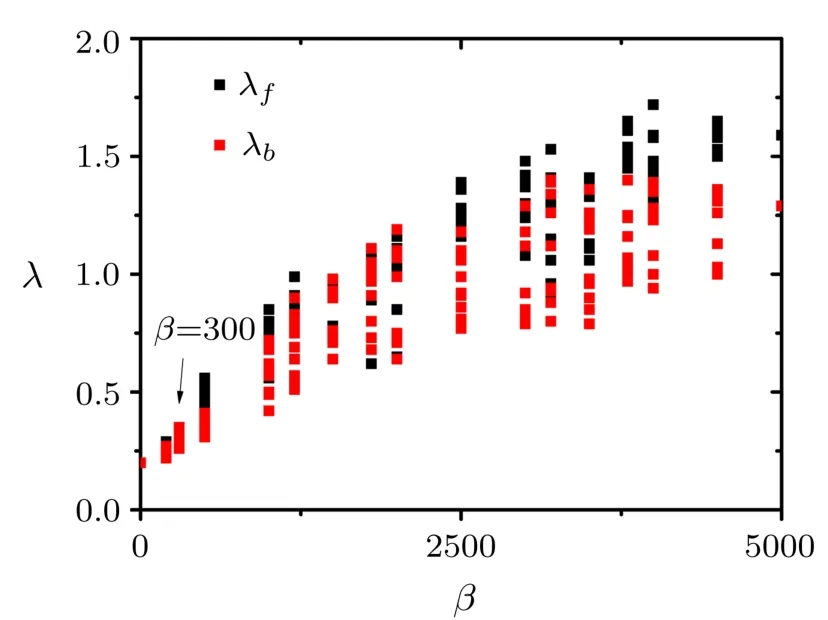
Fig.3(Color online)The coupling strengthes λfin the forward continuation diagram and λbin the backward continuation diagram are plotted against the correlation factor β for ten realizations.The distribution of natural frequency follows the degree distribution of the underlying networks.N=5000 and 〈k〉=6.

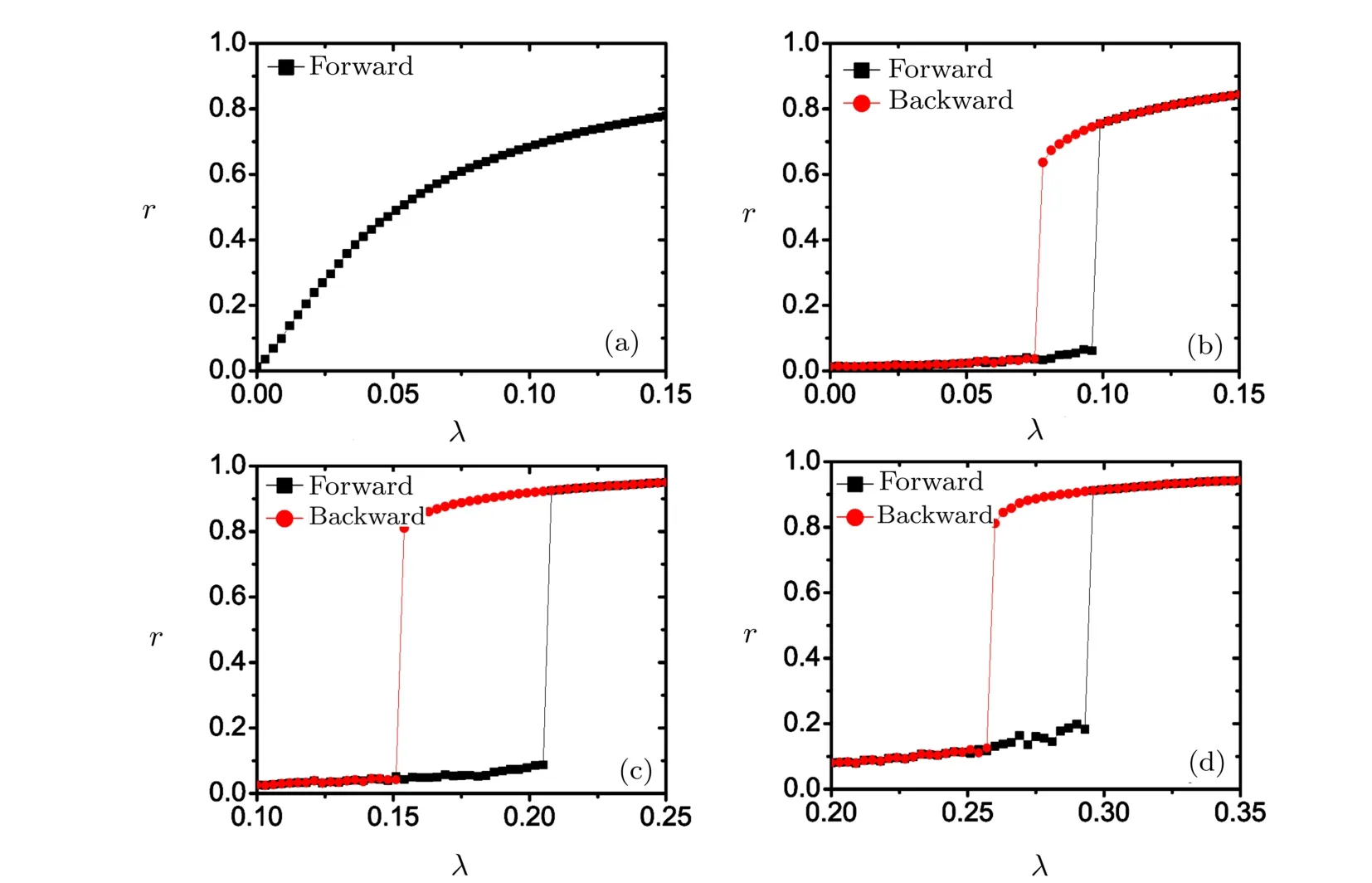
Fig.4(Color online)The synchronization diagrams r(λ)at diあerent correlation factors β for a Kuramoto model on BA networks.g(ω)follows a Lorentzian distribution with γ =0.1 and 〈ω〉=0.(a) β =1;(b)β =1800;(c)β =4000;(d)β =5000.These plots show both forward and backward continuations in λ with the increment of λ at 0.01.N=5000 and 〈k〉=6.

4 Conclusions

In conclusion,we numerically investigate the synchronization transition in a Kuramoto model on scale-free networks.We have introduced a quantity β,the correlation factor,to characterize the correlation between the structural and the dynamical properties in the model.We found that the synchronization transition may be a continuous one for low correlation factor β and a discontinuous one(or explosive synchronization)otherwise.We also found that the critical coupling strengthes for the onset of synchronization out of the incoherent state and for the oあset of synchronization to the incoherent state depend on the correlation factor β.These two critical coupling strengthes and the range of coupling strength for the coexistence of the incoherent state and synchronous states increase with β in an overall way.We also found that the dependence of synchronization transition on the correlation factor can be found in the case that other types of probability distributions of natural frequencies such as Lorentzian distribution are adopted.

[1]N.Wiener,Nonlinear Problems in Random Theory,MIT Press,Cambridge,MA(1958).

[2]S.H.Strogatz,Nonlinear Dynamics and Chaos:With Applications to Physics,Biology,Chemistry,and Engineering,Persus,New York(1994).

[3]A.Arenas,A.D′?az-Guilera,J.Kurths,Y.Moreno,and C.Zhou,Phys.Rep.469(2008)93.

[4]J.A.Acebr′on,L.L.Bonilla,C.J.P.Vicente,F.Ritort,and R.Spigler,Rev.Mod.Phys.77(2005)137.

[5]N.A.M.Ara′ujo,H.Seybold,R.M.Baram,H.J.Herrmann,and J.S.Andrade,Phys.Rev.Lett.110(2013)064106.

[6]M.Rohden,A.Sorge,M.Timme,and D.Witthaut,Phys.Rev.Lett.109(2012)064101.

[7]Y.Kuramoto,Chemical Oscillations,Waves and Turbulence,Springer,New York(1984).

[8]D.Yuan and J.Z.Yang,Commun.Theor.Phys.59(2013)684.

[9]H.Y.Yang,S.Zhang,and G.D.Zong,Commun.Theor.Phys.55(2011)185.

[10]F.E.N.Hassan,M.Paulsamy,F.F.Fernando,and H.A.Cerdeira,Chaos 19(2009)013103.

[11]Y.Moreno and A.F.Pacheco,Europhys.Lett.68(2004)603.

[12]A.Arenas,A.D′?az-Guilera,and C.J.Perez-Vicente,Phys.Rev.Lett.96(2006)114102.

[13]C.Zhou and J.Kurths,Chaos 16(2006)015104.

[14]J.G′omez-Garde?nes,Y.Moreno,and A.Arenas,Phys.Rev.Lett.98(2007)034101.

[15]Y.Liu,J.J.Slotine,and A.L.Barab′asi,Nature(London)473(2011)167.

[16]D.Achlioptas,R.M.D’Souza,and J.Spencer,Science 323(2009)1453.

[17]F.Radicchi and S.Fortunato,Phys.Rev.Lett.103(2009)168701.

[18]Y.S.Cho,J.S.Kim,J.Park,B.Kahng,and D.Kim,Phys.Rev.Lett.103(2009)135702.

[19]J.G′omez-Garde?nes,S.G′omez,A.Arenas,and Y.Moreno,Phys.Rev.Lett.106(2011)128701.

[20]I.Leyva,R.Sevilla-Escoboza,J.M.Buld′u,I.Sendi?na-Nadal,J.G′omez-Garde?nes,A.Arenas,Y.Moreno,S.G′omez,R.Jaimes-Re′ategui,and S.Boccaletti,Phys.Rev.Lett.108(2012)168702.

[21]A.L.Barab′asi and R.Albert,Science 286(1999)509.

[22]J.G′omez-Garde?nes and Y.Moreno,Phys.Rev.E 73(2006)056124.

[23]P.Ji,T.K.DM.Peron,P.J.Menck,F.A.Rodrigues,and J.Kurths,Phys.Rev.Lett.110(2013)218701.