狀態(tài)依賴下不確定切換線性系統(tǒng)有限時(shí)間穩(wěn)定性分析
王躍華,孫曉靚
(1.沈陽(yáng)大學(xué) 理學(xué)院,遼寧 沈陽(yáng) 110044;2.遼寧水利職業(yè)學(xué)院,遼寧 沈陽(yáng) 110122)
對(duì)于現(xiàn)有的關(guān)于切換系統(tǒng)穩(wěn)定性的研究成果,近些年主要側(cè)重在Lyapunov漸近穩(wěn)定問(wèn)題上,也就是表現(xiàn)在無(wú)限的時(shí)間間隔里系統(tǒng)達(dá)到穩(wěn)定.然而在實(shí)際應(yīng)用中,人們更多地考慮的是在一定時(shí)間間隔內(nèi)系統(tǒng)的各種行為.因此,從實(shí)際角度出發(fā),人們側(cè)重于研究的是系統(tǒng)的有限時(shí)間穩(wěn)定問(wèn)題.有限時(shí)間穩(wěn)定性問(wèn)題在文獻(xiàn)[1]中初次被提及.具體地說(shuō),系統(tǒng)的有限時(shí)間穩(wěn)定也就是要滿足當(dāng)系統(tǒng)的初始條件有界時(shí),在有限時(shí)間內(nèi)系統(tǒng)的狀態(tài)可以達(dá)到預(yù)先設(shè)定的界限.顯然,這與Lyapunov漸近穩(wěn)定是不同的.一個(gè)系統(tǒng)可以是有限時(shí)間穩(wěn)定的但是又未必是漸近穩(wěn)定的,這在文獻(xiàn)[2]中被提到,并且有限時(shí)間穩(wěn)定的一些早期的結(jié)論可以在文獻(xiàn)[3-5]中找到.
1 問(wèn)題的提出與帶有不確定項(xiàng)的切換線性系統(tǒng)的描述
考慮一系列如下形式的切換線性控制系統(tǒng):
對(duì)于系統(tǒng)(1),選取如下切換狀態(tài)反饋控制器:
u(t)=Kσ(t)x(t).
(3)
將式(3)代入切換線性系統(tǒng)(1),就可以得到如下形式的閉環(huán)系統(tǒng):
2 相關(guān)假設(shè)與引理
假設(shè)1x(t)的曲線是處處連續(xù)的,也就是切換線性系統(tǒng)的狀態(tài)x(t)在切換的瞬間是不會(huì)發(fā)生跳躍的.
為了確定切換子系統(tǒng)的Lyapunov類函數(shù),整個(gè)狀態(tài)空間Rn需要被分割成若干個(gè)子空間,記作Ωi.為了達(dá)到這個(gè)目的,需要使這些Ωi區(qū)域覆蓋整個(gè)狀態(tài)空間,也就是需要滿足如下覆蓋條件:
Ω1∪Ω2∪…∪Ωm=Rn.
(4)
為了簡(jiǎn)化問(wèn)題,這里假設(shè)每個(gè)區(qū)域Ωi都可以表示成如下二次形式:
Ωi={x∈Rn|xTQix≥0} (i=1,2,…,m).
(5)
式中,Qi∈Rn×n是對(duì)稱矩陣.
下面的引理給出了滿足覆蓋條件的一種有效方法.
引理1[6](覆蓋條件) 如果對(duì)于每一個(gè)狀態(tài)x∈Rn,都有
(6)
成立,那么Ω1∪Ω2∪…∪Ωm=Rn.其中,θi≥0(i=1,2,…,m).
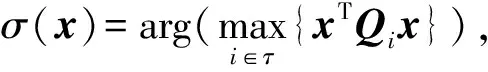
3 有限時(shí)間穩(wěn)定的定義
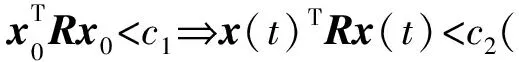
4 有限時(shí)間穩(wěn)定的充分條件及證明
對(duì)于系統(tǒng)(1),選取切換狀態(tài)反饋控制器u(t)=Kσ(t)x(t),將其代入切換線性系統(tǒng)(1),就可以得到如下形式的閉環(huán)系統(tǒng):
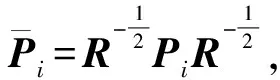
(11)
(12)

證明 令
V(x)=Vi(x)=xTPix
(13)
作為L(zhǎng)yapunov備選函數(shù)用來(lái)測(cè)量每一個(gè)區(qū)域Ωi的能量.這里不妨設(shè)i=1,2;j=1,2.對(duì)于i,j為其他值的一般情況也是顯然的.
第一種情況:當(dāng)滑膜現(xiàn)象不發(fā)生時(shí).
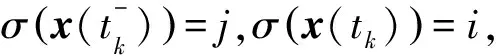
(14)
由式(7)可得
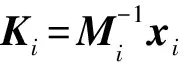
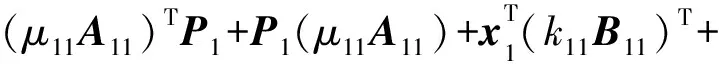
(k11B11)x1+(μ12A12)TP1+P1(μ12A12)+
(19)
(k21B21)x2+(μ22A22)TP2+P2(μ22A22)+
(20)
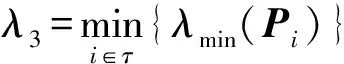
(21)
對(duì)其從tk到t求解可得
V(x) (22) (23) 由式(21)和式(22)可以得到 根據(jù)式(10)以及式(24)~式(26)可以得到 (27) 則根據(jù)定義可知,連續(xù)時(shí)間切換線性系統(tǒng)(1)是有限時(shí)間穩(wěn)定的. 第二種情況:當(dāng)滑膜現(xiàn)象發(fā)生時(shí). 當(dāng)滑膜現(xiàn)象發(fā)生時(shí),在狀態(tài)處滿足如下關(guān)系式: 也就是在子系統(tǒng)發(fā)生變化時(shí)會(huì)產(chǎn)生滑膜現(xiàn)象.滑膜現(xiàn)象可能在區(qū)域Ωi,j處發(fā)生,也就是滿足如下關(guān)系式: xTQix=xTQjx≥0. 滑膜現(xiàn)象會(huì)導(dǎo)致在切換表面產(chǎn)生或者穩(wěn)定或者不穩(wěn)定的動(dòng)力系統(tǒng),因此,需要研究定理中給定的條件是否能夠保證在滑膜現(xiàn)象發(fā)生時(shí)切換系統(tǒng)仍然是有限時(shí)間穩(wěn)定的.當(dāng)滑膜現(xiàn)象在超平面Ωi,j處發(fā)生時(shí),也就意味著滿足如下關(guān)系式: 式中:i=1,2,…,m,j=1,2,…,m.也就是要滿足如下關(guān)系式: 因此,在滑膜表面的系統(tǒng)可以表示成 其中,ρ∈[0,1].由定理中的不等式可得 由此可得 式(33)和式(34)相加可得 同時(shí)有 式(36)和式(37)相加可得 αxTλ3x<αxTPjx. (38) 從而可以得到 (39) 也就是 (40) 因?yàn)槭?21)和式(29)同樣適用于滑膜表面的系統(tǒng),因此,剩下的證明過(guò)程和第一種情況相同. 本文主要研究了在狀態(tài)依賴切換策略下,帶有不確定項(xiàng)的切換系統(tǒng)的有限時(shí)間穩(wěn)定性問(wèn)題.與以往的文獻(xiàn)側(cè)重于運(yùn)用時(shí)間依賴切換策略相比,本文研究的狀態(tài)依賴切換策略更加復(fù)雜,由于切換常數(shù)有時(shí)不會(huì)事先給出,因此,本文研究的狀態(tài)依賴切換策略就顯得更加實(shí)用. 參考文獻(xiàn): [1] Dorato P.Short Time Stability in Linear Time-Varying Systems[C]∥Proceedings of the IRE International Convention Record: Part 4.New York,1961:83-87. [2] Amato F,Ariola M,Dorato P.Finite-Time Control of Linear Systems Subject to Parametric Uncertainties and Disturbances[J].Automatica,2001,37(9):1459-1463. [3] Weiss L,Infante E.Finite Time Stability under Perturbing Forces and on Product Spaces[J].IEEE Transactions on Automatic Control ,1967,12(1):54-59. [4] Li Shihua,Wang Zhao,Fei Shumin.Finite-Time Control of a Bioreactor System Using Terminal Sliding Mode[J].International Journal of Innovative Computing,Information and Control ,2009,5(10B):3495-3504. [5] He Shuping,Liu Fei.Robust Finite-Time Stabilization of Uncertain Fuzzy Jump Systems[J].International Journal of Innovative Computing,Information and Control,2010,6(9):3853-3862. [6] Pettersson S.Synthesis of Switched Linear Systems[C]∥Proceedings of the 42nd IEEE Conference on Decision and Control.Maui,2003:5283-5288. [7] Zhao Guanglei,Wang Jingcheng.Finite Time Stability and L2-gain Analysis for Switched Linear Systems with State-Dependent Switching[J].Journal of the Franklin Institute,2013,350(5):1075-1092.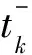
5 結(jié) 語(yǔ)

