TIAN Xiang-Jun

1International Center for Climate and Environment Sciences, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China

2State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China

A Local Implementation of the POD-Based Ensemble 4DVar withR-Localization

TIAN Xiang-Jun1,2

1International Center for Climate and Environment Sciences, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China

2State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China

The purpose of this paper is to provide a robust and flexible implementation of a proper orthogonal decomposition-based ensemble four-dimensional variational assimilation method (PODEn4DVar) throughR-localization. WithR-localization, the implementation of the local PODEn4DVar analysis can be coded for parallelization with enhanced assimilation precision. The feasibility and effectiveness of the PODEn4DVar local implementation withR-localization are demonstrated in a two-dimensional shallow-water equation model with simulated observations (OSSEs) in comparison with the original version of the PODEn4DVar withB-localization and that without localization. The performance of the PODEn4DVar with localization shows a significant improvement over the scheme with no localization, particularly under the imperfect model scenario. Moreover, theR-localization scheme is capable of outperforming theB-localization case to a certain extent. Further, the assimilation experiments also demonstrate that PODEn4DVar withR-localization is most efficient due to its easy parallel implementation.

PODEn4DVar,R-localization, local implementation

1 Introduction

The ensemble Kalman filter (EnKF, Evensen, 1994, 2004; Houtekamer and Mitchell, 1998, 2001; Hamill et al., 2001) provides an advanced alternative solution to data assimilation in various weather (Snyder and Zhang, 2003; Tong and Xue, 2005; Chen and Snyder, 2007; Meng and Zhang, 2008; Wang et al., 2008; Whitaker et al., 2008; Aksoy et al., 2009; Dowell and Wicker, 2009; Torn and Hakim, 2009; Bonavita et al., 2010; Miyoshi et al., 2010) and climate applications (Whitaker et al., 2004; Compo et al., 2011). Besides its simple conceptual formulation and relative ease of implementation, EnKF has the ability to evolve flow-dependent estimates of forecast error covariance by forecasting the statistical characteristics. However, the EnKF does not include the temporal smoothness constraint assumed in the standard four-dimensional variational assimilation method (4DVar, e.g., Lewis and Derber, 1985; Le Dimet and Talagrand, 1986; Courtier and Talagrand, 1987; Courtier et al., 1994) because its design concept incorporates observational information sequentially. Thus, significant efforts have been devoted to enhance data assimilation by coupling 4DVar with EnKF to combine their strengths (e.g., Lorenc, 2003; Qiu et al., 2007; Tian et al., 2008, 2011; Tian and Xie, 2012; Zhang et al., 2009; Cheng et al., 2010; Wang et al., 2010). The proper orthogonal decomposition (POD)-based ensemble four-dimensional variational assimilation method (referred to as PODEn4DVar; Tian et al., 2008, 2011; Tian and Xie, 2012) is proposed based on POD and ensemble forecasting techniques. In the PODEn4DVar, the original ensemble coordinate system is transformed into an optimal scheme under the usual Euclidean norm (Ly and Tran, 2001) through the POD process, which improves assimilation performance. Its feasibility and effectiveness have been demonstrated through the use of an idealized model with simulated observations (Tian et al., 2011; Tian and Xie, 2012) and the Weather Research and Forecasting (WRF) model with real radar data (Pan et al., 2012). Moreover, PODEn4DVar also provides a promising method for land data assimilation (Tian et al., 2009, 2010).

In ensemble data assimilation, localization is generally adopted to ameliorate the spurious correlations of observations from distant regions that occur in analyses (e.g., Houtekamer and Mitchell, 2001; Hamill et al., 2001), thus providing better results in many cases (e.g., Greybush et al., 2011; Miyoshi et al., 2010; Szunyogh et al., 2008). Additionally, analysis at each grid point can be implemented independently with only local observations and the values at nearby model grid points needing consideration; thus, more efficient parallelization of the code can be realized (Hunt et al., 2007; Szunyogh et al., 2008; Greybush et al., 2011).

As discussed by Greybush et al. (2011), two classes of localization techniques in general usage includeB-localization andR-localization. The former operate on background error covariancesB, while the latter are those that modify observation error covariancesR. Although it has been developed mainly in the EnKF community, the localization technique is also indispensable in ensemble-based variational assimilation methods (e.g., Tian et al., 2008, 2011; Tian and Xie, 2012; Wang et al., 2010). The PODEn4DVar uses a variation ofB-localization, in whichthere is no direct modification on the observation error covarianceR(Tian et al., 2011; Tian and Xie, 2012). Unfortunately, previous studies note that both types of localization can disrupt the relationships and thus result in unrealistic imbalances between mass and wind fields in analysis ensembles (e.g., Kepert, 2009; Greybush et al., 2011). Because theB-localization scheme is more prone to imbalance and greater errors in analysis and forecasting, implementation ofR-localization in PODEn4DVar has the potential for improving assimilation performance.

The main purpose of this paper is to describe a local implementation for PODEn4DVar through theR-localization scheme with emphasis on facilitating its parallel coding with improved assimilation performance. The rest of the paper is organized as follows. In section 2, we describe the local implementation for PODEn4DVar withR-andB-localization schemes after a simple review of PODEn4DVar. In section 3, observing system simulation experiments (OSSEs) are conducted with no localization and withR- andB-localization schemes for evaluation of PODEn4DVar. Finally, a summary is given in Section 4.

2 Local implementation for PODEn4DVar through R-localization

2.1 Review of PODEn4DVar

The incremental format of the 4DVar cost function is formulated as

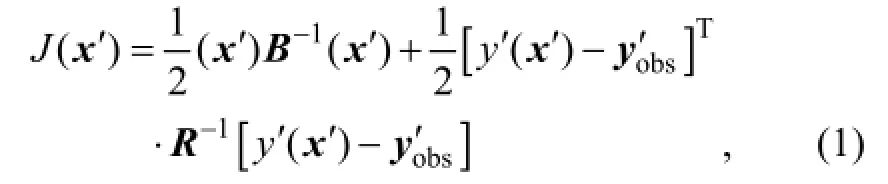
whereχ′ =χ-χbis the perturbation of the background fieldχbat the initial timet0,

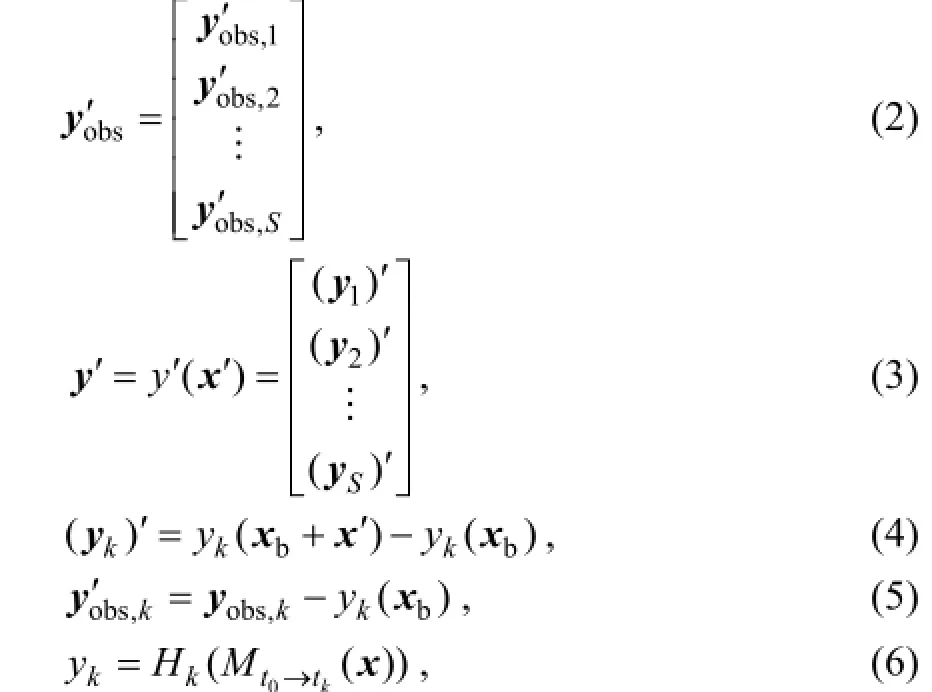
and

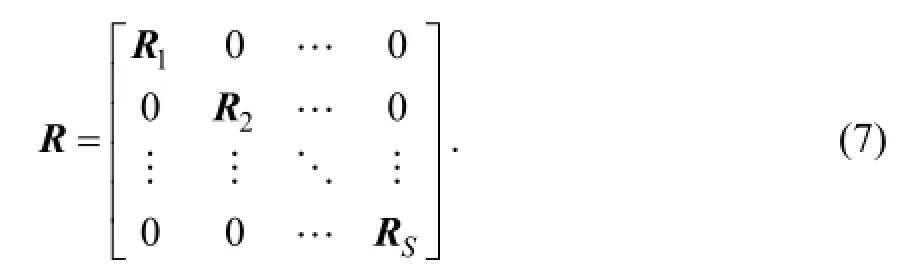
Here, the superscript T represents a transpose, b denotes background value, indexkstands for observation time,Sis the total observational time steps in the assimilation window,Hkacts as the observation operator, and matricesBandRkare the background and observational error covariances, respectively. In this study,Rkis assumed to be diagonal. The 4DVar cost Eq. (1) should be minimized to obtain an optimal increment of initial condition (IC),χ′a, att0, where the subscript a denotes an optimal value, obs denotes the observational values.

In PODEn4DVar (Tian et al., 2011), an ensemble ofNobservation perturbations (OPs)y′:y1′,y′2,… ,y′N, is first generated by using the observation operatorHk, the forecast model, and the initial model perturbations (MPs)χ′:χ1′ ,χ2′,… ,χ′N. Subsequently, the POD transformation to the OP matrixy′ and then to the MP matrixχ′yields

and

whereVis an orthogonal matrix,Λis a diagonal matrix,PχandPyare the POD-transformed MP and OP matrixes, respectively.

The optimal solutionχ′aand its corresponding optimal OPy′ais thus expressed by linear combinations of the POD-transformed MPs and OPs, respectively, as

and

whereβis the coefficient vector.

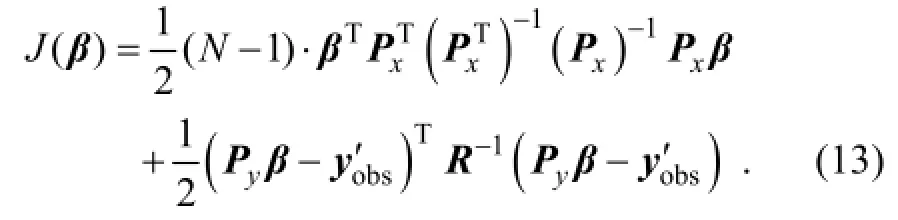
Through simple calculations reported by Tian et al. (2011), the solution to the increment of analysis is simplified into the following form:

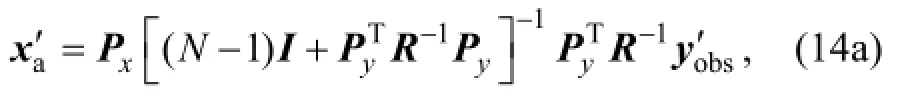
whereIis the unit matrix.

Substituting Eq. (10) into Eq. (14a), the expression can be modified as

The final PODEn4DVar analysis without localization is easily obtained as

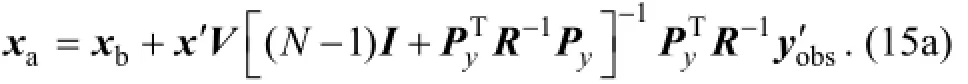
Obviously, Eq. (15a) can be implemented independently for each [ith, 1≤I≤dim(χb)] grid point as

whereχ′g,χb,g, andχa,grepresent MPs, background, and analysis states for each (ith) grid point, respectively.

Conversely, the analysis ensemble perturbation matrix is updated through

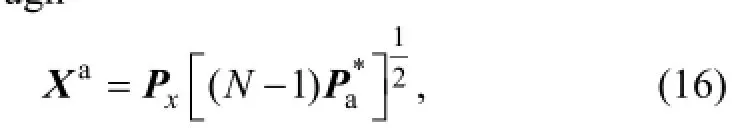
2.2 Local implementation for PODEn4DVar

It is reasonable to assume thatRis diagonal with uncorrelated observation errors. Hunt et al. (2007) proposed a gradualRlocalization by multiplying the diagonal elements ofRby an increasing functionρRof distance from the analysis grid point. Because PODEn4DVar shares similar formulations with the local ensemble transform Kalman filter (LETKF; Hunt et al., 2007), we can easily implement theR-localization scheme into the final PODEn4DVar analysis as

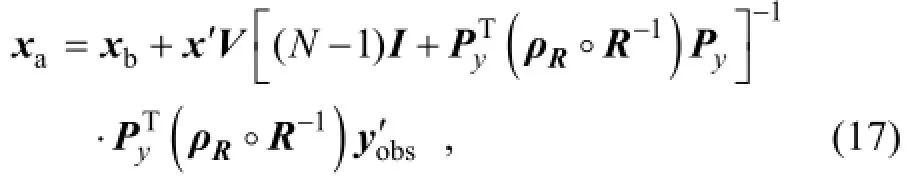
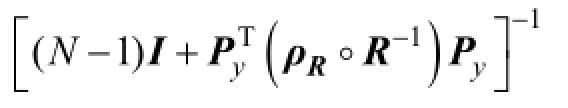
whereρR,gis the local localization matrix,y′obs,gis the local innovation vector,Rgis the local observational error covariance, andPy,gis the local POD-transformed OP matrix.

The local vectors and matrices (i.e.,y′obs,g,Rg,ρR,g, andPy,g) can be formed under the following conditions:

(a) dim(y′obs,g) = 0;

(b) For any 1≤j≤dim(y′obs,g), computeρR,g,j;

(c) IfρR,g,j>ε(whereε> 0 is a small preset parameter), dim(y′obs,g) = dim(y′obs,g)+1; storejin a preset integer vector dimLoc;

(d) All theρR,g,j>εconstitute the local localization matrix,ρR,g;

(e)s= dimLoc(j) [1≤j≤dim(y′obs,g)]; extract all (sth) elements ofy′obs, the (sth) diagonal elements ofR, and the (sth) rows ofPyto construct the local innovation vectory′obs,g, the local observational error covarianceRg, and the local POD-transformed OP matrixPy,g, correspondingly.

Therefore, the local implementation of PODEn4DVar requires the following steps:

1) Run the forecast model repeatedly (Ntimes) to obtain an ensemble ofNobservation perturbations (OPs)y′by using the observation operatorHkand the MPsχ′;

2) (y′)Ty′ =VΛ2VT;

3)Py=y′V;

4) Formy′obs,g,Rg,ρR,g, andPy,gunder the conditions of (a)-(e);

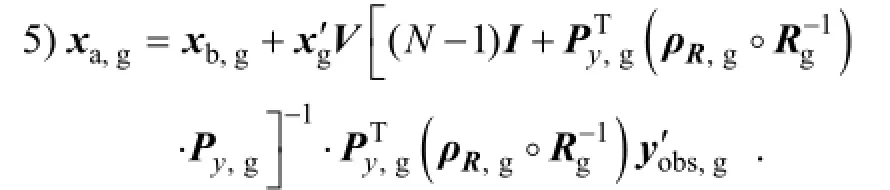
Apparently, the dimensions of the local observational matrices and vectors are substantially lower than the original values because numerous computational resources are thus released. In addition, the implementation of the local analysis steps 1) - 5) is apt to be coded in parallelization.

As mentioned in the Introduction, the original version of PODEn4DVar uses a variation ofB-localization (Tian et al., 2011; Tian and Xie, 2012):

which can be also implemented locally as

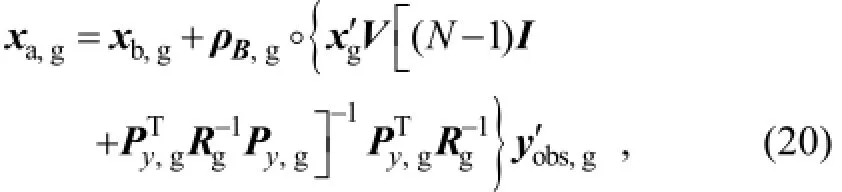
whereρB,gis the local covariance localization matrix.

3 Evaluations within a shallow-water equation model

3.1 Design of OSSEs

To examine the performance of PODEn4DVar withR-localization in comparison with the original version of the method withB-localization and that without localization, it is convenient to design OSSEs by using the same shallow-water equation model with the same parameter settin

gs as that reported by Tian and Xie (2012). Particularly, the model domain is square with 45×45 grid points and periodic boundary conditions ofχ= 0 andLχandy= 0 andLy. The grid spacing isd= Δχ= Δy= 300 km, and the terrain heighthsis defined as

with the maximum height set toh0= 250 m for the true model andh0= 0 m for the imperfect model.

The initial condition and initial ensemble were generated in the same manner as that described by Tian and Xie (2012). Accordingly, the observation errors were assumed to be uncorrelated between different variables and different points in space and time. Simulated observations were generated every 3 h by adding random errors to the model-produced true fields at sparsely selected grids spaced every 3d= 900 km in theχ- andy-directions. The observation error standard deviations were set to 1.5 m forhand 0.21 m s-1foruandv. In all assimilation experiments, the weighting covariance inflation technique proposed by Zhang et al. (2004) was used to relax or weight the previous and updated ensembles; the relaxation coefficient was set toα=0.9. In addition, the period of the data assimilation window in all OSSEs was set toT=12 hours, and the ensemble sizeNwas 100. The default localization function used for all the schemes in this study was the fifth-order piecewise rational function given in Eq. (4.10) of Gaspari and Cohn (1999).

3.2 Experimental results

Figure 1 Spatially averaged (a) height root-mean-square (RMS) errors and (b) wind RMS errors for the proper orthogonal decomposition-based ensemble four-dimensional variational assimilation method (PODEn4DVar) under the imperfect model scenario (h0= 0 m). Schemes without localization and withB- andR-localization are represented by dotted, dashed, and black solid lines, respectively.

A group of experiments in the presence of model error with a maximum terrain height ofh0= 0 m in the forecast model was conducted to investigate the performance levels of all three PODEn4DVar schemes includingB-localization,R-localization, and no localization. Truth simulations (h0= 250 m) were used for verification and for generating observations. Figures 1a and 1b compare the performances of the three schemes under the imperfect model assumption (h0= 0 m). Remarkably, under the imperfect model scenario, the superior performance of theR-localization over the other two schemes was obvious from the beginning of the second assimilation window through the end of the entire assimilation process. Such a conclusion is also strongly supported by the special error statistics over the last assimilation window such that the spatial mean root-mean-square (RMS) error produced by theR-localization scheme was smallest at 3.31 m and 0.57 m s-1for height and wind fields, respectively. Correspondingly, the spatial RMS errors produced by theB-localization scheme were 4.79 m and 0.78 m s-1for height and wind, respectively. No convergent solution was obtained by the no-localization case.

It should be noted that an additional group of experiments under the perfect-model scenario was conducted, and results similar to those of imperfect model case in this study were obtained (not shown). Moreover, the sensitivity of PODEn4DVar withR-localization to parameters such as ensemble size, inflation, and others reported by Tian and Xie (2012) has also been tested.

Table 1 Central processing unit (CPU) time for the PODEn4DVar with various localization schemes.

5 Summary and concluding remarks

This study has upgraded the POD-based ensemble 4DVar method through a local implementation withR-localization. TheR-localization scheme is first introduced to the PODEn4DVar analysis formula, which is followed by a step-by-step description of its efficient local implementation. Local implementation of the original version of PODEn4DVar withB-localization is also presented. For comparison, PODEn4DVar without localization, implemented locally in the same manner as that of localization schemes, is also discussed. The robustness and potential merits of the local implementation of PODEn4DVar withR-localization are demonstrated through OSSEs by using a two-dimensional shallow water model. The local implementation of PODEn4DVar with no localization andB-localization are also adopted to fulfill the same OSSE conditions. The assimilation results imply that the local PODEn4DVar withR-localization outperforms the original version withB-localization to a certain extent, particularly under the imperfect model scenario. An analysis of the computational costs demonstrates that PODEn4DVar local implementation withR-localization is significantly more efficient than the other schemes due to its easy parallelization.

Acknowledgments. This work was supported by the National Natural Science Foundation of China (Grant No. 41075076), the National High Technology Research and Development Program of China (Grant No. 2013AA122002), the Knowledge Innovation Program of the Chinese Academy of Sciences (Grant No. KZCX2-EW-QN207), and the National Basic Research Program of China (Grant Nos. 2010CB428403 and 2009CB421407).

Aksoy, A., D. C. Dowell, and C. Snyder, 2009: A multicase comparative assessment of the ensemble Kalman Filter for assimilation of radar observations. Part I: Storm-scale analyses,Mon. Wea. Rev., 137, 1805-1824.

Bonavita, M., L. Torrisi, and F. Marcucci, 2010: Ensemble data assimilation with the CNMCA regional forecasting system,Quart. J. Roy. Meteor. Soc., 136, 132-145.

Chen, Y. S., and C. Snyder, 2007: Assimilating vortex position with an ensemble Kalman filter,Mon. Wea. Rev., 135, 1828-1845.

Cheng, H., M. Jardak, M. Alexe, et al., 2010: A hybrid approach to estimating error covariances in variational data assimilation,Tellus, 62A, 288-297.

Compo, G. P., J. S. Whitaker, P. D. Sardeshmukh, et al., 2011: The twentieth century reanalysis project,Quart. J. Roy. Meteor. Soc., 137, 1-28.

Courtier, P., and O. Talagrand, 1987: Variational assimilation of meteorological observations with the adjoint vorticity equation II: Numerical results,Quart. J. Roy. Meteor. Soc., 113, 1329-1347.

Courtier, P., J. N. Thepaut, and A. Hollingsworth, 1994: A strategy for operational implementation of 4DVar using an incremental approach,Quart. J. Roy. Meteor. Soc., 120, 1367-1387.

Dowell, D. C., and L. J. Wicker, 2009: Additive noise for stormscale ensemble data assimilation,J. Atmos. Ocean Tech., 26, 911-927.

Evensen, G., 1994: Sequential data assimilation with a nonlinear quasigeostrophic model using Monte Carlo methods to forecast error statistics,J. Geophys. Res., 99(C5), 10143-10162.

Evensen, G., 2004: Sampling strategies and square root analysis schemes for the EnKF,Ocean Dyn., 54, 539-560, doi:10.1007/ s10236-004-0099-2.

Gaspari, G., and S. E. Cohn, 1999: Construction of correlation functions in two and three dimensions,Quart. J. Roy. Meteor. Soc., 125, 723-757.

Greybush, S. J., E. Kalnay, T. Miyoshi, et al., 2011: Balance and ensemble Kalman Filter localization techniques,Mon. Wea. Rev., 139, 511-522.

Hamill, T. M., J. S. Whitaker, and C. Snyder, 2001: Distancedependent filtering of background error covariance estimates in an ensemble Kalman filter,Mon. Wea. Rev., 129, 2776-2790.

Houtekamer, P. L., and H. L. Mitchell, 1998: Data assimilation using an ensemble Kalman filter technique,Mon. Wea. Rev., 126, 796-811.

Houtekamer, P. L., and H. L. Mitchell, 2001: A sequential ensemble Kalman filter for atmospheric data assimilation,Mon. Wea. Rev., 129, 123-137.

Hunt, B. R., E. J. Kostelich, E. Ott, et al., 2007: Efficient data assimilation spatiotemporal chaos: A local ensemble transform Kalman filter,Phys. D, 230, 112-126.

Kepert, J. D., 2009: Covariance localisation and balance in an ensemble Kalman Filter,Quart. J. Roy. Meteor. Soc., 135, 1157-1176.

Le Dimet, F. X., and O. Talagrand, 1986: Variational algorithms for analysis and assimilation of meteorological observations: Theoretical aspects,Tellus, 38A, 97-110.

Lewis, J. M., and J. C. Derber, 1985: The use of the adjoint equation to solve a variational adjustment problem with advective constraints,Tellus, 37A, 309-322.

Ly, H. V., and H. T. Tran, 2001: Modeling and control of physical processes using proper orthogonal decomposition,Math. Comput. Model., 33, 223-236.

Lorenc, A., 2003: The potential of the ensemble Kalman Filter for NWP: A comparison with 4DVar,Quart. J. Roy. Meteor. Soc., 129, 3183-3203.

Meng, Z. Y., and F. Q. Zhang, 2008: Tests of an ensemble Kalman Filter for mesoscale and regional-scale data assimilation. Part IV: Comparison with 3DVAR in a month-long experiment,Mon. Wea. Rev., 136, 3671-3682.

Miyoshi, T, Y. Sato, and T. Kadowaki, 2010: Ensemble Kalman Filter and 4D-Var intercomparison with the Japanese operational global analysis and prediction system,Mon. Wea. Rev., 138, 2846-2866.

Pan, X., X. Tian, X. Li, et al., 2012: Assimilating doppler radar radial velocity and reflectivity observations in the weather research and forecasting model by a proper orthogonal-decomposition-based ensemble, three-dimensional variational assimilation method,J. Geophys. Res., 117, D17113, doi:10.1029/ 2012JD017684.

Qiu, C., A. Shao, Q. Xu, et al., 2007: Fitting model fields to observations by using singular value decomposition: An ensemblebased 4DVar approach,J. Geophys. Res., 112, D11105, doi:10. 1029/2006JD007994.

Szunyogh, I., E. J. Kostelich, G. Gyarmati, et al., 2008: A local ensemble transform Kalman filter data assimilation system for the NCEP global model,Tellus, 60A, 113-130.

Snyder, C., and F. Q. Zhang, 2003: Assimilation of simulated Doppler radar observations with an ensemble Kalman filter,Mon. Wea. Rev., 131, 1663-1677.

Tian, X., and Z. Xie, 2012: Implementations of a square-root ensemble analysis and a hybrid, localization into the POD-based ensemble 4DVar,Tellus, 64A, available at http://dx.doi.org/ 10.3402/tellusa.v64i0.18375.

Tian, X., Z. Xie, and A. Dai, 2008: An ensemble-based explicit four-dimensional variational assimilation method,J. Geophys. Res., 113, D21124, doi:10.1029/2008JD010358.

Tian, X., Z. Xie, A. Dai, et al., 2009: A dual-pass variational dataassimilation framework for estimating soil moisture profiles from AMSR-E microwave brightness temperature,J. Geophys. Res., 114, D16102, doi:10.1029/2008JD011600.

Tian, X., Z. Xie, A. Dai, et al., 2010: A microwave land data assimilation system: Scheme and preliminary evaluation over China,J. Geophys. Res., 115, D21113, doi:10.1029/2010JD014370.

Tian, X., Z. Xie, and Q. Sun, 2011: A POD-based ensemble fourdimensional variational assimilation method,Tellus, 63A, 805-816.

Tong, M. J., and M. Xue, 2005: Ensemble Kalman filter assimilation of Doppler radar data with a compressible nonhydrostatic model: OSS experiments,Mon. Wea. Rev., 133, 1789-1807.

Torn, R. D., and G. J. Hakim, 2009: Ensemble data assimilation applied to RAINEX observations of hurricane Katrina (2005),Mon. Wea. Rev., 137, 2817-2829.

Wang, B., J. Liu, S. Wang, et al., 2010: An economical approach to four-dimensional variational data assimilation,Adv. Atmos. Sci., 27(4), 715-727, doi:10.1007/s00376-009-9122-3.

Wang, X. G., D. M. Barker, C. Snyder, et al., 2008: A hybrid ETKF-3DVAR data assimilation scheme for the WRF model. Part I: Observing system simulation experiment,Mon. Wea. Rev., 136, 5116-5131.

Whitaker, J. S., G. P. Compo, X. Wei, et al., 2004: Reanalysis without radiosondes using ensemble data assimilation,Mon. Wea. Rev., 132, 1190-1200.

Whitaker, J. S., T. M. Hamill, X. Wei, et al., 2008: Ensemble data assimilation with the NCEP global forecast system,Mon. Wea. Rev., 136, 463-482.

Zhang, F., C. Snyder, and J. Sun, 2004: Tests of an ensemble Kalman filter for convective-scale data assimilation: Impact of initial estimate and observations,Mon. Wea. Rev., 132, 1238-1253.

Zhang, F. Q., M. Zhang, and J. A. Hansen, 2009: Coupling ensemble Kalman filter with four dimensional variational data assimilation,Adv. Atmos. Sci., 26, 1-8, doi:10.1007/s00376-009-0001-8.

:Tian, X.-J., 2014: A local implementation of the POD-based ensemble 4DVar withR-localization,Atmos. Oceanic Sci. Lett., 7, 11-16,

10.3878/j.issn. 1674-2834.13.0046.

Received 6 May 2013; revised 20 May 2013; accepted 3 June 2013; published 16 January 2014

TIAN Xiang-Jun, tianxj@mail.iap.ac.cn