A Meshfree Method For Mechanics and Conformational Change of Proteins and Their Assemblies
Ankush Aggarwal,Jiun-Shyan Chenand William S.Klug
1 Introduction and Motivation
Experimental techniques like x-ray crystallography,optical tweezers,atomic force microscope(AFM)and other single molecule experiments[Klug et al.(2006);I-vanovska et al.(2004);Evilevitch et al.(2008);Roos et al.(2009)]provide us with insight into the structure and mechanical properties of biomolecules.Such experimental results are consolidated using theoretical models based upon physical laws to provide in-depth understanding of their mechanical behavior and formulate generalized principles.Proteins have been modeled with full atomic details in molecular dynamics(MD)simulations[Zink et al.(2009)].However,these entail fairly expensive calculations and are,thus,limited by available computational resources to small systems in terms of the number of atoms and length of time.New techniques that make some approximations to bring down the numerical complexity of the problem have been designed.Usually,this is done by reducing the number of degrees of freedom of the system and/or making assumptions about the interaction potential between atoms.These methods,for example elastic network model,Gaussian network model and continuum mechanics,rely on the hypothesis that large wavelength motions and deformations of the proteins are not affected by the fine-scale atomic details,but rather depend on the overall coarse shape.These techniques have been shown to have good accuracy for many cases while making the computations much faster[Tama et al.(2005);Atilgan et al.(2001);Bathe(2008);Gibbons et al.(2008)].
One of the most widely used method—the elastic network model(ENM)assumes that interactions between atoms are spring-like,and,under this assumption,atoms within a certain radius are connected by linear springs.Rotational translational block normal mode analysis(RTB-NMA)adds another assumption that each residue in the protein moves as a rigid-body[Tama et al.(2005)].These methods have been used to calculate the normal modes and fluctuations of proteins.Gaussian network model is a similar method but uses statistical mechanics to define the energy of the system[Atilgan et al.(2001)].Despite the success of these methods,their formulations involve some arbitrary parameters,like the cut-off radius and spring constant which are not physically related to the proteins.Replacing the atomic description of proteins with continuum one has also been successful[Bathe(2008);Gibbons et al.(2008);Aggarwal et al.(2012);Klug et al.(2006)].Finite element method(FEM)is a very well-studied numerical method most commonly used to discretize and solve the governing equations of continuum mechanics[Hughes(2012);Zienkiewicz et al.(1977)].Bathe(2008)presented a framework to apply the finite element method for calculating the normal modes of proteins.Gibbons et al.(2008)used FEM to model the indentation of viral capsids using AFM.Both approaches provided new insights into the mechanics of macromolecules.
The success of FEM has been widespread with applications in a variety of fields–structural analysis,plasticity,electrophysiology,heat transfer etc.However,it has some limitations.Fundamentally,FEM needs a “good-quality”mesh which discretizes the continuum domain,with mesh comprising of discrete “elements”.These elements are usually of polyhedral shape and are used to define the approximation of the field variable,e.g.displacements in elasticity problems.The quality of these elements is determined from factors like their aspect ratio and affects the numerical accuracy of the overall method.For example,equilateral triangles and tetrahedra are good quality elements,while long and narrow “sliver elements”are of bad quality.Creating and maintaining such a good quality mesh presents a challenge and can limit the application of FEM.Mesh generation is often a tedious task which consumes about 80%of the analysis time in industrial applications[Hughes et al.(2005)].Also,the basic finite element shapes like triangles and tetrahedra yield over-stiff results and higher order elements add to the computational cost.Lastly,during large deformations,such as those observed in conformational changes of protein assemblies,an initially good quality mesh usually becomes skewed and needs adaptive remeshing to prevent numerical problems.
In addition to the usual problems related to meshing,application of FEM to biomolecules involves more problems.Since the continuum domain of these biomolecules is not uniquely defined,it is not clear how to discretize them.For calculating the surface bounding the continuum domain of biomolecules,Bathe(2008)used the solvent excluded surface[Sanner et al.(1996)],while Gibbons et al.(2008)used iso-surfacing of a function similar to electron-density.Once a triangulated representation of such bounding surface was obtained,the volume mesh of tetrahedral elements was created by the Delaunay triangulation algorithm[Lee et al.(1980)].Filling of the domain with tetrahedra requires insertion of nodes in between the surfaces.This has also led to more nodes than atoms in Bathe(2008)—an idea contrary to the coarse-graining,and challenges in creating good quality meshes for certain types of biomolecules in Roos et al.(2010).More importantly,the nodes in these methods were placed at positions chosen based upon the element shape criteria and,therefore,did not have direct reference to the atomic positions.In other words,these methods drew only an indirect connection between the atomic and continuum descriptions of macromolecular structures.
In spite of these problems,it is often desirable to use a continuum model because of the efficiency and flexibility it provides.Elastic networks can maintain the kinematic structure of the atomic model,but only indirectly posses continuum-like properties.For example,the ability of large deformation analysis using FEM allowed application to conformational change in virus capsids and provided new insights into their maturation behavior[Aggarwal et al.(2012)],which cannot be achieved with ENM.There have been efforts to develop methods that do not need a mesh to solve continuum mechanics problems,often termed as meshfree[Li et al.(2004)].In this paper,we present a meshfree framework that systematically bridges the gap between the molecular and continuum descriptions of a biomolecule by constructing a continuum model that directly employs the atomic degrees of freedom.This allows for the first time,a one-to-one mapping between the two models.The Reproducing Kernel Particle Method(RKPM)[Chen et al.(1996);Liu et al.(1995)]is used to approximate a function in terms of nodal values.To calculate the domain integrals in weak form of the governing equations,stabilized non-conforming nodal integration(SNNI)[Chen et al.(2007)]is used,where only nodal coordinates and their corresponding volumes are needed as input.It should be noted that the current method uses the same constitutive approximations as in[Bathe(2008);Gibbons et al.(2008)],that of homogeneous isotropic elasticity.However,nodes in this case can be chosen as a subset of atoms of the system(for most of the proteins,atomic coordinates with good resolution are available from the x-ray crystallography or cryo-EM[Westbrook et al.(2002)]).This gives us a direct association between the nodes and the atomic positions,which makes the flow of information from atomic system to the continuum model(or vice-versa)straightforward.The utility and robustness of this framework is demonstrated through three different problems–calculation of atomic fluctuations,large-deformation indentation simulation and analysis of strains related to the conformational changes in viruses.
This paper is organized as follows:next we present the details of protein structures we want to model using proposed method and describe the quantities of interest we seek to calculate.These examples are chosen to demonstrate the robustness and utility of this novel framework.We present the mathematical formulation of this framework,including the details of approximation and integration,followed by the solution techniques used.Then,we present some validation and convergence studies of the new stabilizing kernel we observe.This framework is applied to chosen example problems and the results are presented,which are compared to the experiments and other available methods.We conclude with a summary of the contributions of present framework and discuss the possible future developments using this method.
2 Methods
The key length scales of protein structures range from a few nanometers for single proteins to micrometers for assemblies of several proteins in a well defined arrangement.We use the following structures to demonstrate and validate our framework.
?T4-lysozyme is a small protein with 164 amino acids(also termed as residues).
The atomic coordinates have been determined using X-ray crystallography and are available on the protein data bank(PDB ID–3LZM)[Westbrook et al.(2002)].
?ADP bound G-actin is a slightly larger protein with 375 residues(PDB ID–1J6Z).
?CCMV is a plant virus made up of 180 copies of a protein in T=3 arrangement(according to Caspar-Klug classification[Caspar et al.(1962)]),which is similar to a truncated icosahedron shape.Each of those proteins are made up of around 200 amino acids with a total of approximately 400,000 atoms(including hydrogen)in the capsid.The fully packaged CCMV capsid exists in two distinct structural states.The native structure of the wild-type CCMV capsid,which is stable at pH 5 either with or without the genome,has an average diameter of approximately 28 nm and an average inner diameter of about 21 nm.As the pH is raised to about 7 at low ionic strength,a reversible swelling transition occurs in which the average radius increases by approximately 20%to 33 nm as shown in Fig.2.For the native form,the atomic coordinates of asymmetric unit are available on protein data bank(PDB ID–1CWP)and of the full capsid on viperdb[Shepherd et al.(2006)].Model atomic coordinates of swollen form are available on viperdb.
?HK-97 is a double stranded DNA bacteriophage that attacks E.coli and related bacteria.It is made up of 420 copies of proteins arranged in a left-handed T=7 arrangement[Caspar et al.(1962)].It first assembles into a prohead state and,then,goes through a maturation process constituting several stages.It starts from a prohead state(diameter=53.2 nm)and DNA is packaged into the capsid using a motor protein.Next,it goes through various expansion intermediate stages(EI)which are accompanied by other chemical reactions that lead to changes in size,shape and mechanical properties of the capsid.The final head(H)state is the infectious particle.Three of these states used in present study are shown in Fig.2(PDB IDs–1IF0(P-II),3DDX(EI-II)and 2FT1(H-II)).
?Hepatitis B virus(HBV)is an enveloped animal virus which exists in polymorphic forms.Here we consider two different forms–T=4 arrangement with 240 proteins and an average diameter of about 30 nm(single protein PDB ID–1QGT),and T=3 arrangement with 180 proteins and an average diameter of 25 nm(pseudo-atomic model,unpublished structure from Steven et al.).HBV capsid structure poses special challenges in meshing due to the sharp protrusions on the surface.
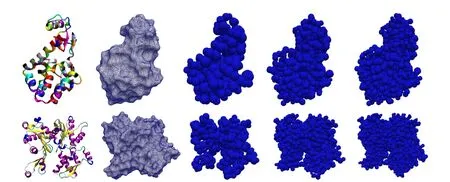
Figure 1:Left to right:Cartoon ribbon diagram of the atomic structure;solvent excluded surface;Meshfree model with nodes at only alpha carbons;with nodes at all carbons;with nodes at all atoms for(Top)T4 lysozyme and(Bottom)G-actin proteins.
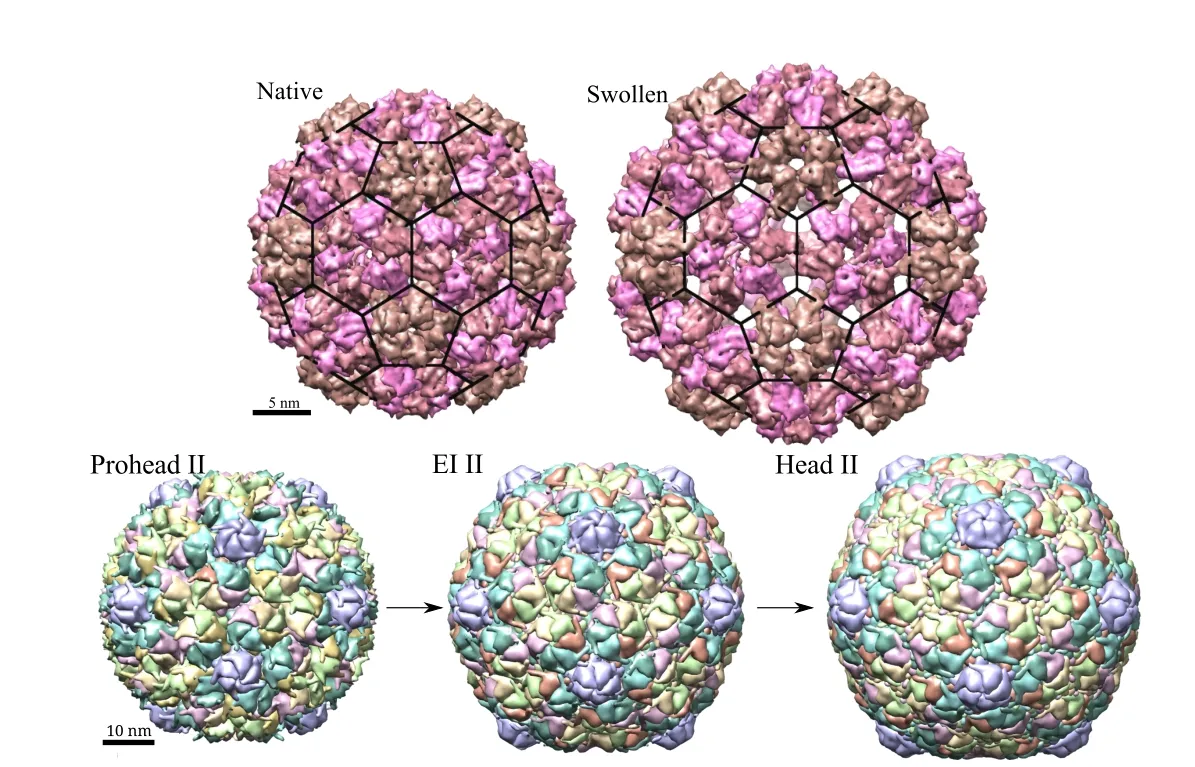
Figure 2:(Top)CCMV structure in native and swollen configurations and(Bottom)HK97 structure changes during maturation.Three distinct stages are shown here.
To demonstrate the capabilities of current method,we solve three specific problems for the above structures:
1.Under thermal energy the protein structure fluctuate around their minimum energy configuration.These fluctuations in the atomic positions can be quantified in an average sense using normal mode analysis and equipartition theorem.The normal mode analysis can be performed with a variety of methods.Fluctuations,thus calculated,give an insight into the mechanical properties of the protein and the mechanical coupling between different parts of it.
2.Atomic force microscopy(AFM),originally invented for imaging surfaces,has been widely used for calculating force response of nano-scale structures.Experimental results are available for the force response of many virus capsids during indentation with AFM tip.This experimental setup can be simulated using continuum mechanics to calculate the force-displacement relation and compared to the experimental results to provide an estimate of capsid’s elastic modulus.Such an analysis on different configurations of the same virus provides insights into the assembly and infection mechanisms.
3.Conformational changes in virus capsids,e.g.,of CCMV with pH change and HK-97 during maturation,are fundamentally due to changes in the molecular interactions that in-turn affect the mechanical properties of capsid as a whole.However,very little is known about these changes in terms of continuum description.We seek to calculate the strains associated with such conformational variations in viruses and determine their relation to changes in global mechanical properties.This kind of analysis is almost impossible with the conventional finite element based methods but becomes straightforward with the method presented here.
These problems can be framed mathematically using the continuum theory of large deformation elasticity.We start with a generalized form including all the terms and then,later,specialize them to each specific problem.
2.1 Mathematical Formulation
Continuum mechanics describes an object as a continuous domain where material fills up all the points in the domain. To use such an approximation for biomolecules,which are arguably discrete,a consistent domain needs to be defined first from the atomic coordinates.This is done using the solvent excluded surface[Sanner et al.(1996)],which is the domain carved out by the closest point of a sphere of solvent molecule as it rolls over the macromolecule defined by atomic van der Waals spheres.Once this domain is determined,we formulate the conventional continuum elasticity theory for the system.


number of points in the domain.These points,often termed as nodes,are the points of interest where solution is sought.In the context of biomolecules,it is natural to ask for these points to be related to atoms.Thus,the nodes in this study are chosen as a subset of the atoms or their linear combination,e.g.,unweighted centeroids of the atoms in each amino acid in the polypeptide chain of protein referred to as“residue centers”.Here it is required that the atomic coordinates are known with high resolution,which is true for a large number of proteins from cryo-EM or x-ray crystallography,coordinates being available online at protein data bank[Westbrook et al.(2002)].Furthermore,the number of nodes can be chosen as per desired accuracy and resolution of the numerical solution.Three different refinement levels for two proteins—T4-Lysozyme and G-Actin are shown in Fig.1.
The displacement field()in integral/weak form of the governing equation(Eq.2)is replaced with an approximation().So the Galerkin problem statement is:

Following the conventional FEM,tessellation of nodes by the Delaunay algorithm could be used to construct piecewise polynomial shape functions.However,highly non-uniform spacing of the atoms,and thus the nodes,leads to highly skewed tetrahedra resulting in a bad approximation properties and poor numerical accuracy of the solution.To avoid that,we use a meshfree technique which does not need a connectivity and defines the shape functions solely based on the node positions.A commonly used approximation in meshfree methods is the Reproducing Kernel(RK)approximation[Chen et al.(1996,2003)]and its details are presented next.
2.2 Reproducing Kernel Particle Method(RKPM)
Reproducing kernel(RK)shape function()is assumed to be of the form:


In other words,the kernel approximation should be able to reproduce the basis functions exactly up to ordern(and hence the name–Reproducing Kernel).Applying the reproducing condition gives us the following matrix equation for coefficientsbi
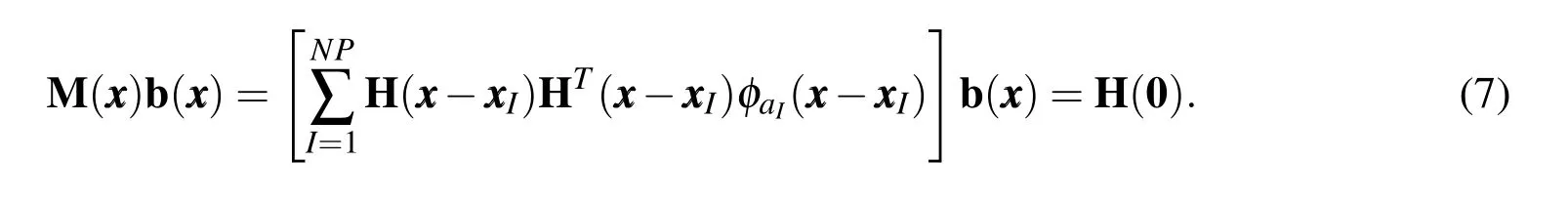
Equation(7)can be solved forbito get the shape function.The RK shape functions have the same continuity as that of the kernel function and,in general,are non-interpolating,i.e.ΨI()6=δIJ.The lack of Kronecker delta property means that the coefficients of the approximation are not equal to the displacement at the nodes which poses some complexity in applying displacement boundary conditions and implementing contact type constraints.In the present context of modeling the mechanics of biomolecules,the lack of a Kronecker delta property also presents a challenge in associating nodes with atomic coordinates,which is the key objective of our model.To recover the Kronecker delta property,Chen et al.(2003)modified the kernel approximation to have two parts:

Under the three combined conditions that 1)Eq.(9)holds,2)the primitive functionis of the form:

The above equation can be simplified to get

force vector.Although it is possible to derive the analytical form of the stiffness matrix components[cf.Zienkiewicz et al.(1977)],in current formulation,for simplicity,it is calculated by numerically differentiating the internal force vector.To evaluate these components of mass matrix and internal/external force vectors,an integration over the domain ? is required.Since the shape functions are zero everywhere except the nodal domain,these integrations can be localized.The integration technique has an effect on the overall stability of the framework and the numerical method to evaluate these integrals is discussed next.
2.3 Numerical Integration
For numerically calculating the domain integral in Eq.(13),Gaussian quadrature rule is commonly used in conventional FEM.Ap-th order Gaussian quadrature rule gives exact integration result for polynomials of an order up to 2p?1.However,as can be seen from Eq.(7),the RKPM shape functions are rational functions and Gaussian quadrature cannot give exact integration.This leads to inexact integration resulting in spurious zero-energy modes in the stiffness matrix and instabilities of the numerical method unless very high order quadrature rule is used.Also,applying Gaussian quadrature rule requires definition of a background mesh which may not match the domain of influence of the RK shape functions and adds to the complexity of the problem setup.To solve all these problems,in the present framework we use nodal integration.
The components of mass matrixreplacing the integral with values as the node.That is

Since our shape functions have Kronecker delta property,it simplifies to MIJ=ρ0VIδIJ,giving us a diagonal mass matrix.Similarly,the external force vector is simply the external force at boundary node multiplied by the surface area of that nodal domain.
For evaluating the internal force vector,and thus the stiffness matrix,we need spatial derivatives of the shape functions at the nodes.Instead of using exact derivatives of the shape functions,“smoothed"derivatives were shown to remove the spurious zero-energy modes in nodal integration by Chen et al.(2001).It was shown that the exact derivatives pass the patch test in analytical form but not discrete form,whereas smoothed derivatives pass linear patch test in the discrete form. Therefore,numerical convergence and stability using the smoothed derivatives are superior to that using the exact derivatives.Smoothed derivatives are defined as an average over the nodal domain,i.e.

where ?Lis the nodal domain ofLthnode andVLis its volume.Nodal domain is usually taken as the Voronoi cell corresponding to that node(Fig.3).Applying divergence theorem,the volume integral in the above equation can be replaced by a surface integral

This surface integral is calculated using 20 integration points located equidistant on a sphere(taken as the 20 vertices of a dodecahedron inscribed inside that sphere).This approximation makes the computation significantly easier as the only information needed is the volume corresponding to the nodes and their positions.No underlying grid or any other information about the nodal domain is required.Using this shape function derivative,the deformation gradient becomes
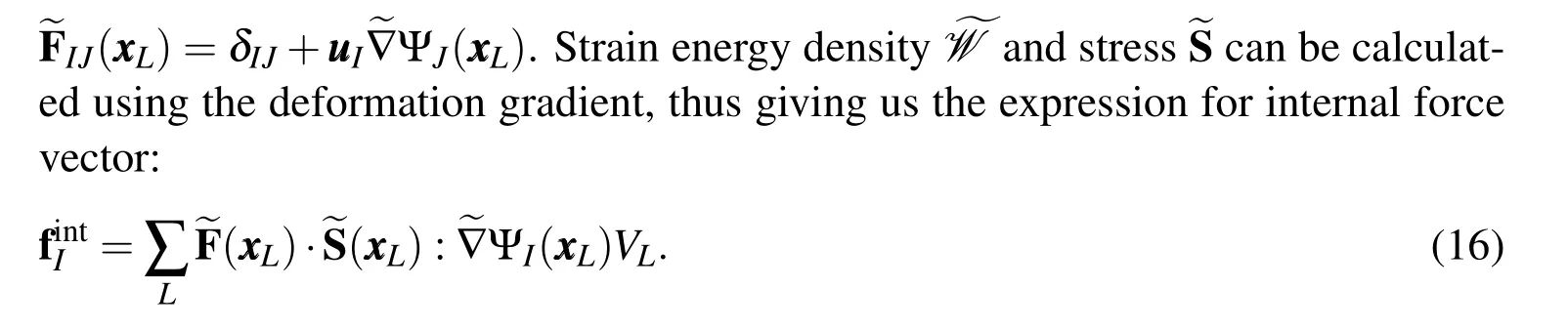
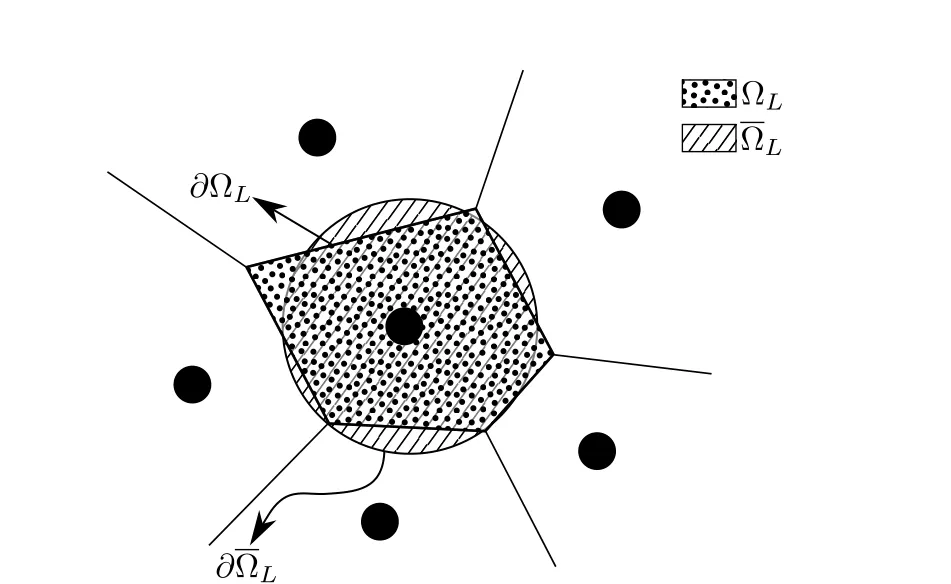
Figure 3:Stabilized non-conforming nodal integration(SNNI)approximates the nodal domain as a simplified shape(spherical here)instead of the exact voronoi tessellation simplifying the formulation
2.4 Determination of Nodal Domain
For determining nodal domains,the positions of the nodes are calculated directly from the atomic coordinates,which in turn are available from protein data bank.Usually,the nodal domains are represented by Voronoi tessellation of nodal point cloud.However,in three-dimensions and for non-convex domain boundaries,it is not straightforward to determine the Voronoi tessellation.Therefore,instead we focus on calculating only the nodal volumes.We use the Delaunay algorithm to tessellate the nodal set[Si et al.(2006)].For each tetrahedra,a quarter of its volume is assigned to each of its four nodes to give us the nodal volumes.In general,(unconstrained)Delaunay tessellation procedures create a tetrahedral mesh of the convex hull of a point cloud.Biomolecule boundaries are generally not convex,so when we tessellate the node set we get some tetrahedra that are outside the biomolecule boundary.To remove these extra tetrahedra,the solvent excluded surface(SES)is calculated using the program MSMS[Sanner et al.(1996)]and any tetrahedra lying outside this surface are removed.
SES is defined as the surface carved out when a solvent sphere roles on the molecule.Here,a probe radius of 6 ? is used so as to obtain all the necessary details of surface without getting any artificial holes.In MSMS program’s algorithm,by default,the solvent molecule approaches the surface from infinity.This calculates the outer surface of protein in a very efficient way.However,this does not calculate the inner surface of structures like virus capsids.In order to obtain both inner and outer surfaces,we decompose the structure into two hemispherical parts and then use MSMS algorithm to get two surfaces.Then these are combined to obtain the final SES surface and used for the removal of extra tetrahedra.
Using the nodal volumes and smoothed derivative formulation presented in this section,expressions of the mass matrix,external and internal force vector,and stiffness matrix are evaluated.The support sizeaIis assigned same for all the nodes in our model.It is chosen as the minimum value such that the matrix M in Eq.(11a)is non-singular at all the nodes in our system.The minimum possible support size is chosen so that the accuracy of approximation can be maximized.Usually,the support size thus determined comes out to be in the range of 7–12 ?.The governing equations thus obtained can be formulated for specific problems.Details of the solution procedures are presented in the next section.
2.5 Solution Procedures
2.5.1Normal Modes
The governing equation(Eq 13c)obtained using meshfree formulation can be assembled into a matrix form:
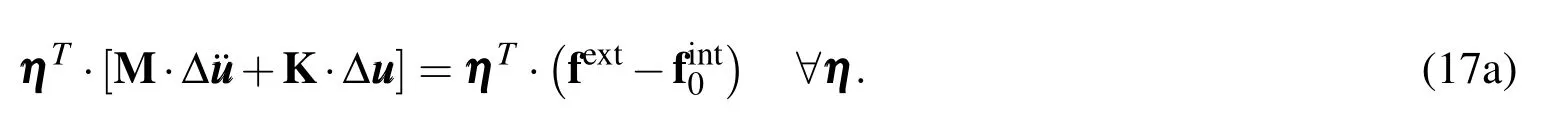
Arbitrariness of η implies that it can be dropped to give us the final equation of motion

Given the applied forces and initial conditions,this equation can be integrated in time and solved iteratively to obtain the trajectory of motion.In the absence of external forces and when linearized with respect to the reference configuration(i.e.=0),the equation further simplifies to

The above equation,often termed as the normal mode equation,can be converted into a generalized eigenvalue problem.It is done by assuming the solution of the form=(k)eiωkt,which gives the eigenvalue problem

This equation can be solved to obtain 3Nmode shapes(eigenvectors,Nbeing the number of nodes in the system) and mode frequencies(eigenvalues ωk).Normal modes can also be computed using other methods–elastic network model and molecular dynamics,which yield the same form of equation as Eq(18).However,in those cases,the stiffness matrix K is defined as the Hessian of potential energy V with respect to degrees of freedom of the system about the minimum energy configuration:KIJ= ?2V/?uuuI?uu
uJ|0.In the case of elastic network model,the potential energy is the sum of spring energies,and in the case of MD,it is the sum of bonded and non-bonded interactions[Vanommeslaeghe et al.(2010)].In all of these cases,the mass matrix M is diagonal and thus the eigenvalue problem(18)can be simplified to

2.5.2Indentation and Pressurization
For quasi-static problems like indentation of virus capsids with spherical tip and pressurization of a thick elastic sphere, the inertia term can be dropped from general governing equation(Eq.13b).Keeping the internal force vector as it is(instead of replacing it with the linearized stiffness matrix expression)and dropping the virtual displacement η because of its arbitrariness,we get the governing equationThis equation is solved iteratively using quasi-Newton method based limited memory BFGS solver[Zhu et al.(1997)].For applying the internal pressure in thick sphere,the external force vector is simply calculated using pressure force in radial direction.For indentation simulation,the external force is zero.However,the rigid indentor introduces constraints on the boundary,where the contact friction is set to be high enough(μ=1)to avoid any slipping.The contact constraint from AFM is implemented using the augmented Lagrange algorithm.The indentor is modeled with a rigid flat plate at the bottom for the substrate and a rigid sphere of radius 20 nm at the top for the AFM tip.
3 Results
3.1 Effect of Different Kernels on Stability
In most of the applications using RKPM based meshfree method,a cubic B-spline function is used for the kernel function(andin Eqns.(9-11a)).However,that results in instability from the soft modes.As discussed in the section 2.3,nodal integration reduces the computation complexity and cost,but,usually,poses problems of numerical instability and spurious energy modes.It is known that using SCNI/SNNI removes the spurious zero energy modes but,still,exhibits soft modes[Puso et al.(2008)].In Puso et al.(2008),an additional stabilization was introduced to suppress those soft modes.To investigate this numerical instability,we turn to a simpler problem of calculating the normal modes of a regular elastic 3D solid(Young’s modulus=200 MPa,Poisson’s ratio=0.4,density=1 g/mm3and size=10×10×10 mm3).The instability can be observed while looking at the first four non-zero energy normal modes of a regular elastic 3D solid(using a cubic B-spline kernel which hasC2continuity)as shown in Fig.4.Similar instability is observed when using quintic B-spline and linear kernels withC4andC0continuity respectively(not shown here).
In the framework presented here,we use instead a constant kernel withC?1continuitywhich was observed to suppress the soft modes(Fig.4).Furthermore,SNNI method approximates the nodal domain as a simplified shape—usually a cube or sphere.This approximation leads to an assumed strain calculated as the average over some neighborhood of the node.The neighborhood size varies slightly based upon assumed domain shape.To full determine the effect of the size of the smoothing neighborhood zone,we introduce an additional parameter α such that

approximately the same rate of convergence but different absolute errors,with cubic kernel being more accurate than the constant kernel,in general.However,the normal modes of three dimensional solid indicated that constant kernel is more accurate than the cubic one(Fig.4).To examine the effect of problem dimensions on the numerical accuracy,we numerically solve the problem of a thick pressurized sphere,for which the exact solution is known.The analytical solution for the linear compressible Hookean response(Poisson’s ratio ν =0.3)is compared to the numerical solution in Fig.5b.It is clear that for a three dimensional analysis the cubic kernel gives higher error compared to the constant kernel.
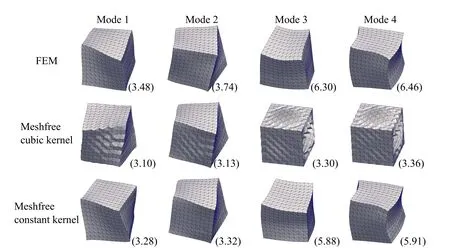
Figure4:First four non-zero energy normal modes of an elastic cube using different methods with their eigenfrequencies ?×10?6?provided in the parentheses.
3.2 Thermal Fluctuations
In this section,normal modes are computed for two small proteins–T4 lysozyme(PDB ID-3LZM)and ADP-bound G-actin(PDB ID-1J6Z),which are further used to calculate their average thermal fluctuations using theorem of equipartition.The results are compared against other benchmark methods of elastic network model and all atomic MD potentials.
General solution of the governing equation of motion without external forces(E-q.17c)can be obtained by superposition of 3Nlinearly independent solutions of eigenvalue problem(Eq.19):

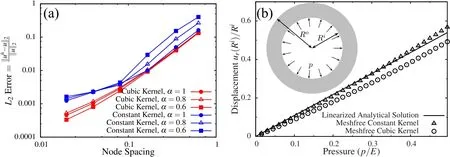
Figure 5:(a)Error calculation for the 1D Poisson’s equation,considering constant and cubic kernel functions with different α values and(b)comparison of numerical solution with analytical solution for a 3D thick pressurized sphere

The normal modes and mean-squared thermal fluctuations of each residue are thus calculated using different methods.The all atomic potentials as defined in CHARMM force field[Vanommeslaeghe et al.(2010)]are used to get the benchmark(All Atom MD)results which do not involve any scaling factor.Elastic network model is used with rotational-translational block assumption(RTB),where the eigenvalues and,thus,the thermal fluctuations are proportional to the spring constant[Tama et al.(2005)].The continuum elasticity based meshfree(MF)method presented here also gives results which can be scaled with the elastic modulusE,if the Poisson’s ratio ν is held constant.Our method is verified against the previous two methods by calculating the thermal fluctuations at three levels of refinement–one node per residue,one node per carbon atom and one node per atom.For the summation in above equations,lowest 30 eigenvectors are considered.The RMS fluctuations of the two proteins calculated by different methods are shown in Fig.6.The results from different methods match well and overlap for the most part.To quantify the similarity between different results in Fig.6,their correlations are calculated as
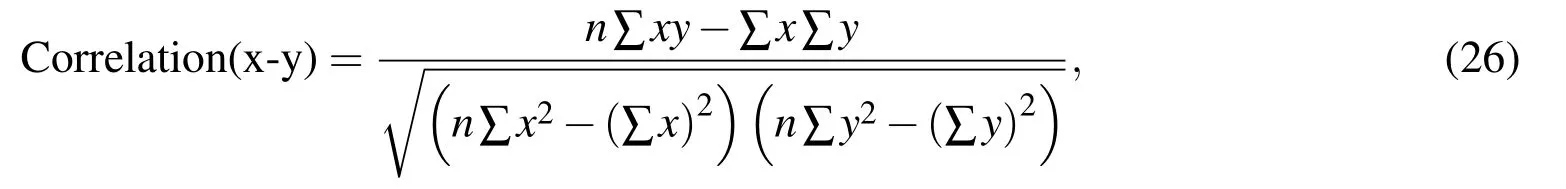
and are listed in Tab.1.The MF results match extremely well with the RTB results and do not change significantly upon refinement,thus,indicating convergence.Such convergence can not be obtained with regular cubic kernel because of stability issues demonstrated in the last section.The experimental values are obtained from the B-factors in pdb files,and are only a rough estimate of the RMSF values.The correlations of these experimental B-factors with the current meshfree results are within an acceptable range.Also,the current method performs as well as the RTB and finite elements[Bathe(2008)].The contour plots of cross-correlationsCabfor the two proteins are shown in Fig.7.The close similarity between different plots again demonstrates the agreement between current method and RTB,and the convergence of meshfree results upon refinement.
3.3 AFM Indentation
Indentation of viral capsids using atomic force microscope(AFM)is an important experimental technique for probing their mechanical properties.The results have been theoretically explained using continuum mechanics solved by finite element method[Gibbons et al.(2007,2008);Michel et al.(2006)].Here,meshfree method is used to simulate the indentation of cowpea chlorotic mottle virus(CCMV)native capsid.The meshfree nodes are defined at the α-carbon positions from the atomic coordinates available at[Shepherd et al.(2006)].
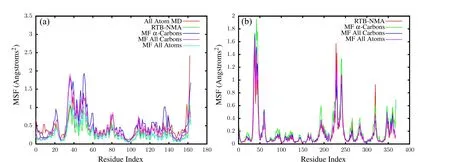
Figure 6:Root mean square fluctuations= for T4-Lysozyme(a)and G-Actin(b)–The values with meshfree converge with refinement and are in agreement with the results using RTB and all atom MD.
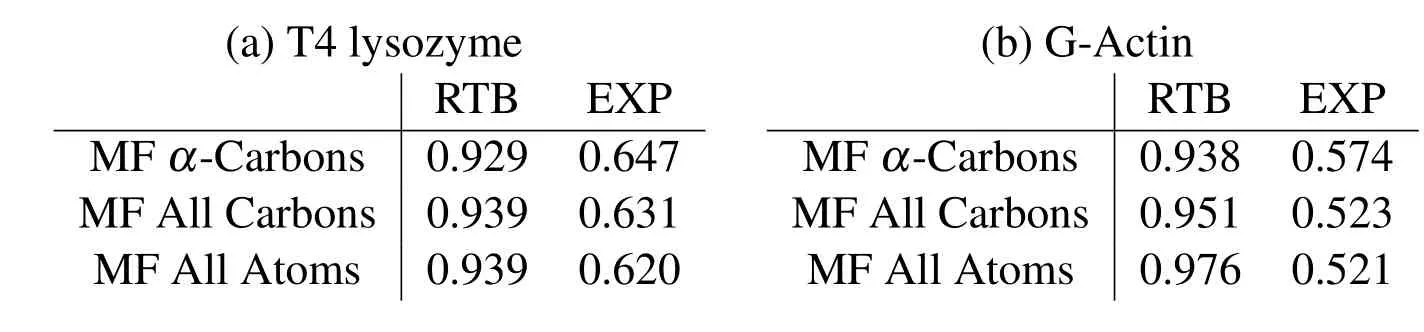
Table 1:Correlations of RMSF calculated by meshfree(MF)method with the elastic network model(RTB)and experimental B-factor(EXP)
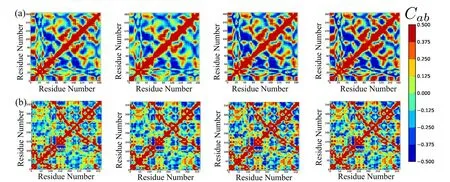
Figure 7:Cross correlation of fluctuations using(from Left to Right)RTB-NMA,meshfree α-carbons,all carbons,all atoms for T4-Lysozyme(a)and G-Actin(b)
In Fig.8 results are compared to the results from FEM [Gibbons et al.(2008)].Both cases are calculated with compressible neo-Hookean material withμ0lnJ+(I1?3)with Poisson’s ratio of 0.4.When scaled to the experiments,shape of the force-displacement curve are quite similar.But,the effective Y-oung’s modulus comes out to be 290 MPa using FEM and 493 MPa using meshfree method.That is,the results from meshfree method show a softer response by a factor of around 1.7.Thismaybe due to two reasons.In FEM,tetrahedral elements are used which usually give a stiffer response.Mesh refinement(both p-and h-refinement)has been observed to affect the FEM results slightly[Gibbons(2008)].Secondly,the method used to create the mesh in Gibbons et al.(2008)uses a Gaussian shaped electron-like density of atomic coordinates.The chosen width of the Gaussian density function affects the thickness of the generated mesh,and the requirement of a good quality mesh means that it tends to overestimate the thickness of the capsid resulting in a stiffer response.
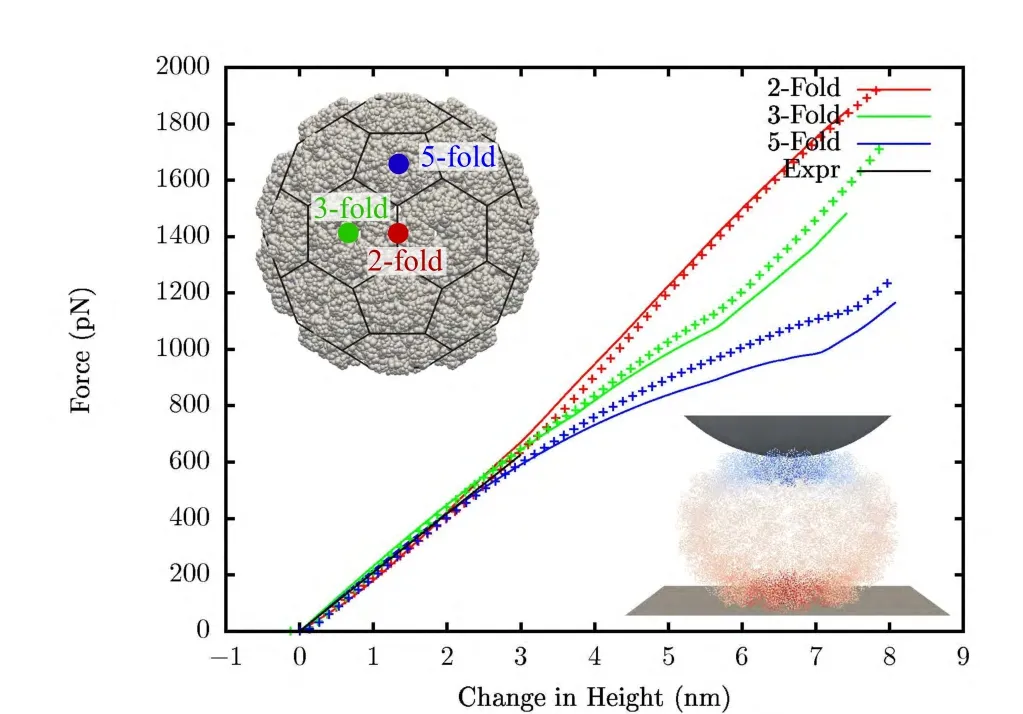
Figure 8:Indentation simulation of native CCMV:lines are results using meshfree and crosses are using FEM.Inset shows the meshfree domain with a truncated icosahedron net overlay on it and a deformed shape of the capsid colored by displacement.
To demonstrate the robustness of the present formulation,additional two virus capsids–HK-97 and HBV are simulated under AFM indentation.Two configurations are modeled for each capsid,Procapsid-II and mature Head-II for HK-97,and T=3 and T=4 for HBV virus.Capsids in all of the cases are modeled using the same neo-Hookean material as that used for the CCMV case.The Young’s modulus is chosen to be 200 MPa and the Poisson’s ratio ν =0.4.For HK97,nodes are placed at the center of every third residue,and for HBV at the center of every residue.The resulting force-displacement curves are shown in Fig.9.The indentation response is significantly different for different capsids.The thicker and spherical HK-97 prohead II capsid undergoes a smooth displacement until large deformations of the order of its radius.On the other hand,the thinner and more faceted HK-97 head II has large drops in forces at some indentation associated with buckling events.Current formulation captures the buckling phenomenon extremely well,and the different indentation behavior observed here is consistent with previous thin-shell models of the virus capsids[Klug et al.(2006)]as well as experiments[Roos et al.(2012)].In case of HBV,the structure of capsid poses challenges because of the sharp protrusion of the surface leading to bad quality meshes.However,with the current framework,those limitations are overcome and the indentation response is calculated robustly irrespective of the widely varying mechanical properties of virus capsids.
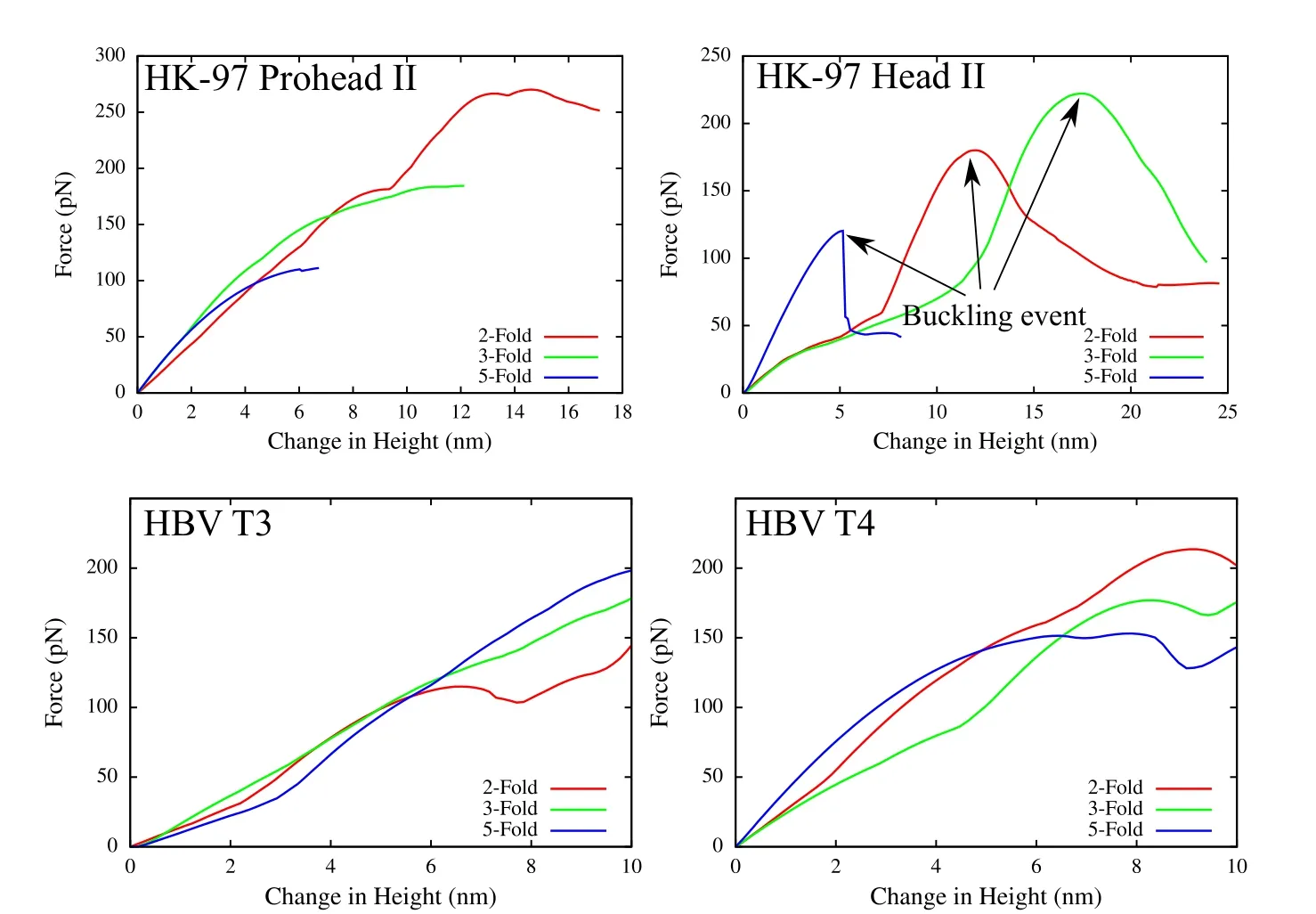
Figure 9:Indentation simulation of HK-97(top)and HBV(bottom)virus capsids in two different configurations each.
3.4 Conformation Change
The meshfree method presented here gives the flexibility of large deformation analysis using any energy potentials or constitutive law while having the degrees of freedom correspond directly to the atomic structure.We demonstrate the utility of these features by analyzing the conformational change of protein assemblies.The analysis presented in this section is not a solution of a governing equation,rather a measure of kinematics.We start from atomic coordinates of a macromolecule in two different states,which are determined experimentally using x-ray crystallography.Then we derive meshfree nodes from those two states,determine the mapping from one state to the other and calculate strains associated with the conformational change.
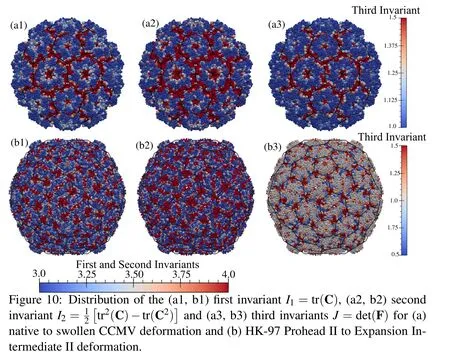
Viruses,during their life cycle or maturation process,undergo various conformational changes.When subjected to an increase in the pH,CCMV goes from a native state to swollen state.This transition has been found to be reversible and is suspected to be related to the genome release mechanism.We analyze the deformation of native to swollen state using the residue centers as nodes with native state as the reference configuration.We calculate the deformation mapping to swollen state using the present method and plot the deformation invariants(Fig.10).It can be seen that most of the deformation is concentrated at the interfaces of the pentamers and hexamers,and at the quasi 3-fold symmetry sites of the truncated icosahedron which open up in the swollen state.
Similarly,the transition of HK-97 virus from its prohead state(PH-II)to expansion intermediate II is analyzed where the hexons change from a skewed shape to a symmetric shape.It is observed that when the prohead state is taken as the reference state,the strains do not show the expected patterns of shear banding.However,when the expansion intermediate state is taken as the reference state,we can clearly see those shear lines along the skew directions at the center of each hexamer(Fig.10).For the most part this transformation is volume conserving except at the vertices of the pentamers and hexamers.It is also found that some points(less than 5%)in this deformation have a negative Jacobian.These points are the sites where conformational motions exhibit sliding of atomistic substructures,thus showing up as inversion of local volumes in the continuum description.
4 Discussion
4.1 Importance of Coarse-Graining Methods
Mechanical analysis of protein assemblies present particular challenges due to the complexity of atomic interactions and large number of particles involved.Based upon the assumption that the coarse scale properties are not dependent upon the detailed molecular interactions,but only on the gross geometric features,the problem can be simplified in many different ways.This has been achieved by various coarse-graining methods each of which possess specific advantages.The application of these methods has provided important insights into many different properties of protein assemblies and helped formalizing generalized principles,which would have been very difficult using models with full atomic details.Two distinct classes of coarse-grained methods are particle-based and continuum-based.The primary aim of the present work was to formulate a method that derives advantages from both classes and bridges the two domains.
4.2 Contribution of the Present Framework
Results calculated using the meshfree framework presented here compare extremely well with other established methods.The thermal fluctuations for T4-lysozyme and G-actin match very well with the elastic network model and converge nicely as the model is refined from one node per residue,to one node per carbon atom and to one node per atom.This is also evident from the correlations between different methods and the cross-correlation contour plots,all of which provide excellent agreement with the RTB-NMA.
Results from AFM indentation show a good agreement between the present formulation and FEM method previously applied.At the same time,it solves many of the problems associated with FEM application.The mesh generation is a time consuming step in finite element analysis,and it becomes even more challenging for complicated structures like that of HBV capsid.Meshfree method presented here solves that problem in a very straightforward way.It provides great robustness while simulating the AFM indentation which,on many occasions,involves sharp buckling phenomenon as seen for the HK97 mature capsid.These indentation results for HK97 match very well with the thin shell model proposed before[Klug et al.(2006)].Such buckling phenomenon are usually extremely hard to capture numerically,however the present formulation handles them in a very robust way.This is especially important since the model for HK97 was a coarse one with only one node per three residues.
In addition to saving the time and effort in meshing,the current method also provides a direct link between the atomic degrees of freedom and the continuum degrees of freedom.This can be considered as a hybrid between the atomic description and continuum description,and is the first such attempt to the authors’knowledge.This presents many advantages:the refinement procedure becomes highly straightforward,where the nodes can be placed at atoms or their subsets.This also can be varied spatially in cases where more details and accuracy are needed in one part of the structure.Furthermore,the information flow between atomic and continuum models becomes easy.This was demonstrated by calculating strains related to conformational changes in two viral capsids(Fig.10).Such results provide important insight into the geometric changes during maturation and how they affect the infectivity.In both cases,the strains are localized to the interfaces between different proteins.The calculated strains associated with the conformational changes can be used in further analysis.Such future possibilities are discussed next.
4.3 Limitations and Future Directions
The strains calculated for conformational changes in virus capsids are a first step in a novel analysis using this hybrid atomic-continuum meshfree method.Such capability opens up many frontiers of future work.These calculated strains can be used in analyzing their effect on the shape change during maturation.In our previous work[Aggarwal et al.(2012)],we constructed an elasticity theory for changes like those of HK97,however the pre-strains were manually estimated from the images in a very coarse way.The detailed strain field calculated here will facilitate that kind of analysis.Also,the analysis presented here was purely kinematic.For CCMV,since the swelling transition is reversible,we can construct an energy potential which has two minima,one at the native state and the other at the swollen state.For example,d? can be constructed and used to determine the least energy pathway between the two states.Such an analysis will allow insight into the conformational changes and transition behavior.These possibilities will be explored in detail in the future.
By virtue of the ease of information flow between continuum and atomic description,coupled approaches can be developed.Such approaches,where the information from atomic model is used in the continuum model and vice-versa,are called multi-scale methods.The present framework is an ideal place to start such an analysis and obtain more detailed insight into protein mechanics.In addition,the present method gives a direct way of tuning the geometric details in continuum model by varying the level of coarse-graining.For example,some nodes in CCMV swelling and HK97 maturation show negative Jacobian indicating a breakdown in the continuum approximation locally.However,with further coarse-graining of atomic motions,the local“internal motions”of the atomic substructure,which produced negative Jacobians,are averaged out,and the negative Jacobians values disappear.This allows for calculating the minimum amount of geometric details needed for certain types of analyses,and answering the overarching question of why continuum mechanics proves to be successful for structures which are obviously discrete.The accuracy of the present method would need further analysis.The constant kernel improves the performance over the generally used cubic kernel,however the frequencies calculated for elastic cube show small errors.The error here can be tolerated given the other assumptions made about protein assemblies and coarse nature of experimental results.The additional stabilization observed by using constant kernel is an unexpected result because smoother approximation functions,in general,give smaller error.The speculated reason is that in SCNI/SNNI,the derivatives of the shape functions are not calculated exactly,and,thus,this method becomes similar to assumed strain method.It is seen that in one dimension,cubic kernel remains more accurate,however,in three dimensions the constant kernel provides less error.Basic numerical studies performed here demonstrate the better performance of constant kernel compared to that of the cubic kernel in three dimensions.The difference in performance could be because of the difference in type of equations being solved,the dimension of the problem(which determines the domain to boundary size ratio),or a combination.To thoroughly understand and prove the convergence properties of this phenomenon,more detailed analysis is required which will be carried out in the future.
4.4 Summary
We presented a framework to apply an RKPM based meshfree method to protein mechanics.The results for small proteins were validated against the elastic net-work model.It was shown to resolve some of the issues with other coarse-graining techniques,e.g.,meshing difficulties in FEM and restriction to small deformation in ENM.At the same time,the direct correspondence between the atoms and nodes allowed us to calculate the strains associated with the conformational change of virus capsid.This method allowed us to quantitatively describe the strains in structures determined to atomic resolution and,also,opens up numerous other possibilities.For example,hierarchical multi-scale homogenization can be done to calculate the spatial variation of the elastic properties of proteins,concurrent multi-scale homogenization can be done using forces from molecular dynamics,anisotropic modeling can be done using stiffer material modulus along the backbone of protein structure etc.Such modeling techniques would make important tools for answering various questions about proteins and their assemblies.
Acknowledgement:We gratefully acknowledge helpful discussions with Chung-Hao Lee.This work was partially supported by National Science Foundation(DMR1006128 and DMR1309423 to W.S.K.)and American Heart Association(14POST 18720037 to A.A.).
Aggarwal,A.;Rudnick,J.;Bruinsma,R.F.;Klug,W.S.(2012): Elasticity theory of macromolecular aggregates.Phys.Rev.Lett.,vol.109,pp.148102.
Atilgan,A.R.;Durell,S.R.;Jernigan,R.L.;Demirel,M.C.;Keskin,O.;Bahar,I.(2001):Anisotropy of fluctuation dynamics of proteins with an elastic network model.Biophysical Journal,vol.80,no.1,pp.505–515.
Bathe,M.(2008):A finite element framework for computation of protein normal modes and mechanical response.Proteins:Structure,Function,and Bioinformatics,vol.70,no.4,pp.1595–1609.
Brooks,B.R.;Jane?iˇc,D.;Karplus,M.(1995):Harmonic analysis of large systems.I.Methodology.Journal of computational chemistry,vol.16,no.12,pp.1522–1542.
Caspar,D.L.D.;Klug,A.(1962): Physical principles in the construction of regular viruses.Cold Spring Harb Symp Quant Biol,vol.27,pp.1–24.
Chen,J.S.;Han,W.;You,Y.;Meng,X.(2003):A reproducing kernel method with nodal interpolation property.International Journal for Numerical Methods in Engineering,vol.56,no.7,pp.935–960.
Chen,J.S.;Hu,W.;Puso,M.A.;Wu,Y.;Zhang,X.(2007):Strain Smoothing for Stabilization and Regularization of Galerkin Meshfree Methods.Meshfree Methods for Partial Differential Equations III,pp.57–75.
Chen,J.S.;Pan,C.;Wu,C.T.;Liu,W.K.(1996): Reproducing kernel particle methods for large deformation analysis of non-linear structures.Computer Methods in Applied Mechanics and Engineering,vol.139,no.1-4,pp.195–227.
Chen,J.S.;Wu,C.T.;Yoon,S.;You,Y.(2001):A stabilized conforming nodal integration for Galerkin mesh-free methods.International Journal for Numerical Methods in Engineering,vol.50,no.2,pp.435–466.
Evilevitch,A.;Fang,L.T.;Yoffe,A.M.;Castelnovo,M.;Rau,D.C.;Parsegian,V.A.;Gelbart,W.M.;Knobler,C.M.(2008): Effects of salt concentrations and bending energy on the extent of ejection of phage genomes.Biophysical journal,vol.94,no.3,pp.1110–1120.
Gibbons,M.M.(2008):Computational mechanics of nanoindentation of viral capsids.PhD thesis,University of California,Los Angeles,2008.
Gibbons,M.M.;Klug,W.S.(2007): Nonlinear finite-element analysis of nanoindentation of viral capsids.Physical Review E,vol.75,no.3,pp.31901.
Gibbons,M.M.;Klug,W.S.(2008): Influence of nonuniform geometry on nanoindentation of viral capsids.Biophysical journal,vol.95,no.8,pp.3640–3649.
Hughes,T.J.R.(2012):The finite element method:linear static and dynamic finite element analysis.Dover Publications.com.
Hughes,T.J.R.;Cottrell,J.A.;Bazilevs,Y.(2005):Isogeometric analysis:Cad,finite elements,nurbs,exact geometry and mesh refinement.Computer methods inapplied mechanics and engineering,vol.194,no.39,pp.4135–4195.
Ivanovska,I.L.;De Pablo,P.J.;Ibarra,B.;Sgalari,G.;MacKintosh,F.C.;Carrascosa,J.L.;Schmidt,C.F.;Wuite,G.J.L.(2004): Bacteriophage capsids:tough nanoshells with complex elastic properties.Proceedings of the National Academy of Sciences of the United States of America,vol.101,no.20,pp.7600.
Klug,W.S.;Bruinsma,R.F.;Michel,J.-P.;Knobler,C.M.;Ivanovska,I.L.;Schmidt,C.F.;Wuite,G.J.L.(2006):Failure of viral shells.Phys.Rev.Lett.,vol.97,pp.228101.
Lee,D.-T.;Schachter,B.J.(1980):Two algorithms for constructing a delaunay triangulation.International Journal of Computer&Information Sciences,vol.9,no.3,pp.219–242.
Li,S.;Liu,W.K.(2004):Meshfree particle methods,volume 11.Springer.
Liu,W.K.;Jun,S.;Li,S.;Adee,J.;Belytschko,T.(1995):Reproducing kernel particle methods for structural dynamics.International Journal for Numerical Methods in Engineering,vol.38,no.10,pp.1655–1679.
Michel,J.P.;Ivanovska,I.L.;Gibbons,M.M.;Klug,W.S.;Knobler,C.M.;Wuite,G.J.L.;Schmidt,C.F.(2006):Nanoindentation studies of full and empty viral capsids and the effects of capsid protein mutations on elasticity and strength.National Acad Sciences.
Puso,M.A.;Chen,J.S.;Zywicz,E.;Elmer,W.(2008): Meshfree and finite element nodal integration methods.International Journal for Numerical Methods in Engineering,vol.74,no.3,pp.416–446.
Roos,W.H.;Gertsman,I.;May,E.R.;Brooks,C.L.;Johnson,J.E.;Wuite,G.J.L.(2012): Mechanics of bacteriophage maturation.Proceedings of the National Academy of Sciences,vol.109,no.7,pp.2342–2347.
Roos,W.H.;Gibbons,M.M.;Arkhipov,A.;Uetrecht,C.;Watts,N.R.;Wingfield,P.T.;Steven,A.C.;Heck,A.J.R.;Schulten,K.;Klug,W.S.et al.(2010):Squeezing protein shells:how continuum elastic models,molecular dynamics simulations,and experiments coalesce at the nanoscale.Biophysical journal,vol.99,no.4,pp.1175–1181.
Roos,W.H.;Wuite,G.J.L.(2009): Nanoindentation studies reveal material properties of viruses.Advanced Materials,vol.21,no.10,11,pp.1187–1192.
Sanner,M.F.;Olson,A.J.;Spehner,J.C.(1996):Reduced surface:an efficient way to compute molecular surfaces.Biopolymers,vol.38,no.3,pp.305–320.
Shepherd,C.M.;Borelli,I.A.;Lander,G.;Natarajan,P.;Siddavanahalli,V.;Bajaj,C.;Johnson,J.E.;Brooks,C.L.;Reddy,V.S.(2006): VIPERdb:a relational database for structural virology.Nucleic acids research,vol.34,no.suppl 1,pp.D386.
Si,H.;TetGen,A.(2006): A quality tetrahedral mesh generator and threedimensional delaunay triangulator.Weierstrass Institute for Applied Analysis and Stochastic,Berlin,Germany.
Tama,F.;Brooks III,C.L.(2005):Diversity and identity of mechanical properties of icosahedral viral capsids studied with elastic network normal mode analysis.Journal of molecular biology,vol.345,no.2,pp.299–314.
Vanommeslaeghe,K.;Hatcher,E.;Acharya,C.;Kundu,S.;Zhong,S.;Shim,J.;Darian,E.;Guvench,O.;Lopes,P.;Vorobyov,I.;Mackerell,A.D.(2010):Charmm general force field:A force field for drug-like molecules compatible with the charmm all-atom additive biological force fields.Journal of Computational Chemistry,vol.31,no.4,pp.671–690.
Westbrook,J.;Feng,Z.;Jain,S.;Bhat,T.N.;Thanki,N.;Ravichandran,V.;Gilliland,G.L.;Bluhm,W.;Weissig,H.;Greer,D.S.et al.(2002):The protein data bank:unifying the archive.Nucleic Acids Research,vol.30,no.1,pp.245.
Zhu,C.;Byrd,R.H.;Lu,P.;Nocedal,J.(1997):Algorithm 778:L-BFGS-B:Fortran subroutines for large-scale bound-constrained optimization.ACM Transactions on Mathematical Software(TOMS),vol.23,no.4,pp.550–560.
Zienkiewicz,O.C.;Taylor,R.L.(1977):The finite element method,volume 3.McGraw-hill London.
Zink,M.;Grubmüller,H.(2009):Mechanical properties of the icosahedral shell of southern bean mosaic virus:A molecular dynamics study.Biophysical journal,vol.96,no.4,pp.1350–1363.
 Computer Modeling In Engineering&Sciences2014年7期
Computer Modeling In Engineering&Sciences2014年7期
- Computer Modeling In Engineering&Sciences的其它文章
- Particle-Based Moving Interface Method for The Study of the Interaction Between Soft Colloid Particles and Immersed Fibrous Network
- Simulations of Blood Drop Spreading and Impact for Bloodstain Pattern Analysis
- Large Deformation Dynamic Three-Dimensional Coupled Finite Element Analysis of Soft Biological Tissues Treated as Biphasic Porous Media
- Preface
