WANG Fang,CUI Wei-cheng(Hadal Science and Technology Research Center,Shanghai Ocean University,Shanghai 201306,China)

Effect of Plastic Zone Size Induced by a Single Dwell Overload on the Fatigue Crack Growth Rate under Cyclic Loading

WANG Fang,CUI Wei-cheng
(Hadal Science and Technology Research Center,Shanghai Ocean University,Shanghai 201306,China)

Creep and fatigue are involved in the loading of deep manned submersible,which is a rather complex variable amplitude pattern.Reasonable assumptions should be made before calculating the room temperature dwell fatigue life.A typical simplified loading type is the cyclic loading with one period of overloaded dwell time.Retardation effects are observed in the prior experimental research while no proper prediction equations were proposed to explain the phenomenon.In this paper,a new prediction model for the load pattern of cyclic loading with a single dwell overload is proposed.Retardation is explained by the increase of monotonic compressive plastic zone size.The calculation methods of the total monotonic plastic zone size in the vicinity of crack tip,due to the overload and the dwell time are provided and the corresponding variation of crack opening level based on the total monotonic plastic zone can be obtained.Tests are conducted to obtain the parameters used in the crack growth models and creep models together with tensile test results of the material TC4 ELI, which is as an example to calculate the retardation effects of overload and dwell time.It is observed that the model can reasonably reflect the retardation effects due to compressive plastic zone in the vicinity of the crack tip induced by dwell time.

crack growth rate;dwell overload;plastic zone size;manned pressure hull

1 Introduction

The pressure hull of deep manned submersibles during their service life will experience periods of both fluctuating and steady stresses.Hence,creep and fatigue are involved,which may act together in a synergistic manner.In order to obtain a proper fatigue design,it is important to consider the real structural loading history,P（）t.Since fatigue failure is a future event,the fatigue loading history for the designed structure can never be known a priori.Many engineering methods are based on finding the worst case scenario,where‘worst’often should be interpreted as a certain severe load condition.Fig.1 gives a schematic representation of typical fatigue loading history with intermittent creep for pressure hull of deep manned submersibles.

The fatigue failure with creep interaction has attracted attention especially in high temperature condition.Typically,linear accumulation model is used to consider the common interaction of fatigue and creep.In recent years,creep effect on fatigue in room temperature is also highlighted,which is often neglected in the past.

In the past four decades,significant effort and progress have been made to study dwell fatigue and pure fatigue behavior of metal alloys to find out how the material responds to dwell time.The prior research attributed dwell sensitivity to many deleterious mechanisms.These mechanisms include:time-dependent strain accumulation,micro-structural and micro-texture influences,stress ratio effects,internal hydrogen embrittlement and environmental effects,crystallographic orientation dependence and interactions between creep and fatigue.However,there is no consensus on the basic cause of the dwell fatigue sensitivity of metal alloys,especially titanium alloys used in submersibles.Up to now,the problem remains opened as well on the scientific as on the engineer point of view.

In 1980,Munz and Bachmann[1]proposed the separation idea to solve the problem.Fig.2 shows the separation of cycles with hold times in cycles with a triangular wave form and a constant load(dwell load).If such a separation is possible, the crack growth rate can be calculated by the addition of two terms:the crack growth rate(da/dN)tiangof a test with a triangular wave form an the crack growth rate da/dt in a constant load test at the stress intensity factor Kmax,corresponding to the maximum load,times the hold time Δt,

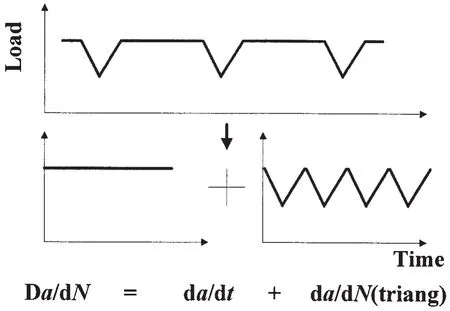
Fig.2 Separation of load cycle with hold time[1]

The linear summation in Eq.(1)is a simplified crack growth evaluation methods which hasbeen applicable to some structural integrity assessment procedure but has not considered the interaction between fatigue and creep damages.Wakai[2]conducted a benchmark study in predicting creep-fatigue crack growth in 316L(N)cracked plates subjected to a cyclic bending moment.The predictions according to different procedures using linear summation expression were compared with each other.Differences are found between the predictions of the methods. Comparing to the experimental data,it is found that the simplified methods exhibit conservatisms which are significantly reduced when integrating the creep curve continuously without initialization during the experiment.

The load history shown in Fig.1 is a variable amplitude load pattern.However,due to the complexity to consider the variable amplitude problem,the load pattern must be simplified. Based on the results in literature,valuable results on the relationship of fatigue,creep and dwell fatigue at room temperature can be summarized as follows:

(1)There will be a‘transition stress level’.The failure sequence among normal fatigue, creep and dwell fatigue will be different when the stress level is lower or higher than the transition stress level.At the lower stress level,the dwell fatigue life(cycles)will be approximate to the cyclic fatigue life(cycles),however,at the higher stress level around or higher than yield stress,damage accumulation will mostly exist in holding time period and the dwell fatigue life will be approximate to the room temperature creep life when the holding time in each cycle is relatively long.

(2)There will be a‘saturated holding time’.At the higher stress level,the holding time length will affect the dwell fatigue life.When the holding time length(may be several minutes or hours)reaches to a certain value that we can call‘saturated holding time’,the dwell fatigue life(hours)will be largely approximate to the creep life(hours).when the holding time is a short period,the dwell fatigue life (cycles)will be approximate to the low-cycle fatigue life(cycles).

According to the above conclusions, several assumption can be made before calculating the room temperature dwell fatigue life in the model for pressure hull submersibles as shown in Fig.1,in the following,

(1)Most of the cycles at the lower stress level can be treated as normal cyclic loading as shown in the base triangle cycles of Fig.3(a);

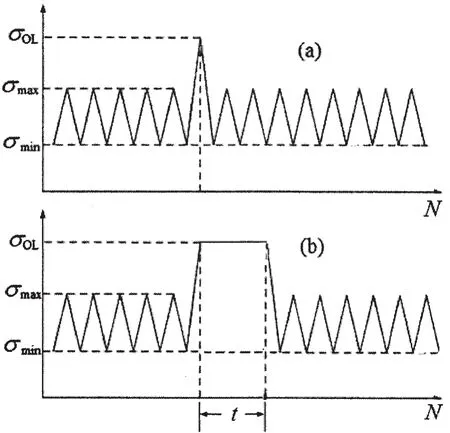
Fig.3 Schematic representation of the load patterns for (a)cyclic loading with one overload and(b)cyclic loading with overloaded dwell time

(2)The cycle with holding time at the higher stress level can be treated as the single/multiple overload with a period of hold-ing time(cyclic loading with overloaded dwell time),as shown in Fig.3(b).

So the cyclic loading with a single dwell overload is a typical simplified load pattern.Overload effect exists when holding stress is higher than base maximum stress.Room temperature creep at a crack tip and its influence on the fatigue crack growth behavior of a 304 stainless steel have been studied by Zhao et al[3].The load patterns of fatigue with dwell time shown in Fig.4 are considered in the test.A time-dependent deformation has been observed at the crack tips under various stress intensity factors.The deformation increases with increasing stress intensity factor.Either acceleration or retardation of fatigue crack growth rate is found after holding time, which depends on the load pattern.Retardation occurs in the load pattern A.A demarcation line is observed on the fracture surface following the holding period. This implies that the crack propagation root or mode changed after the dwell time.Improvement of the prediction equations should be proposed to explain more phenomenon of creep effect on fatigue crack growth rate.

In this paper,a possible model is proposed to consider the load pattern shown in Fig.4(b), based on the unified fatigue life prediction method proposed by the authors’group[4].The study aims at searching for a proper method to consider the effect of plastic zone size induced by a single dwell overload on the fatigue crack propagation under cyclic loading.

2 The model for cyclic loading with a single dwell overload

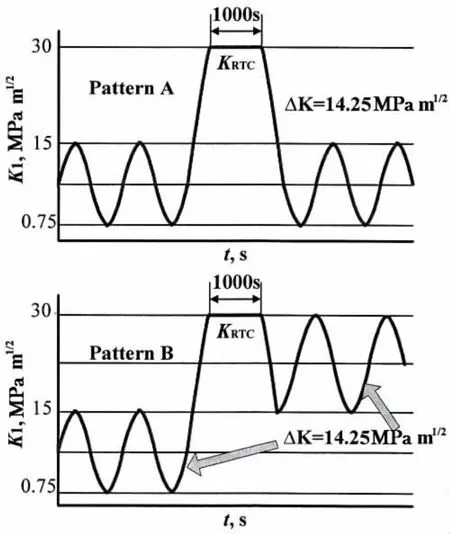
Fig.4 A schematic of load patterns of fatigue with dwell time[3]

The improved constitutive model can be expressed by Eqs.(2)[4].

Considering this phenomenon that at higher load ratio the experimental data are closure free,we propose that the term ΔKeffin the constitution relation is expressed by the above piece-wise function.And Newman’s function[5]for fopis modified by introducing a constraint factor α′as follows:

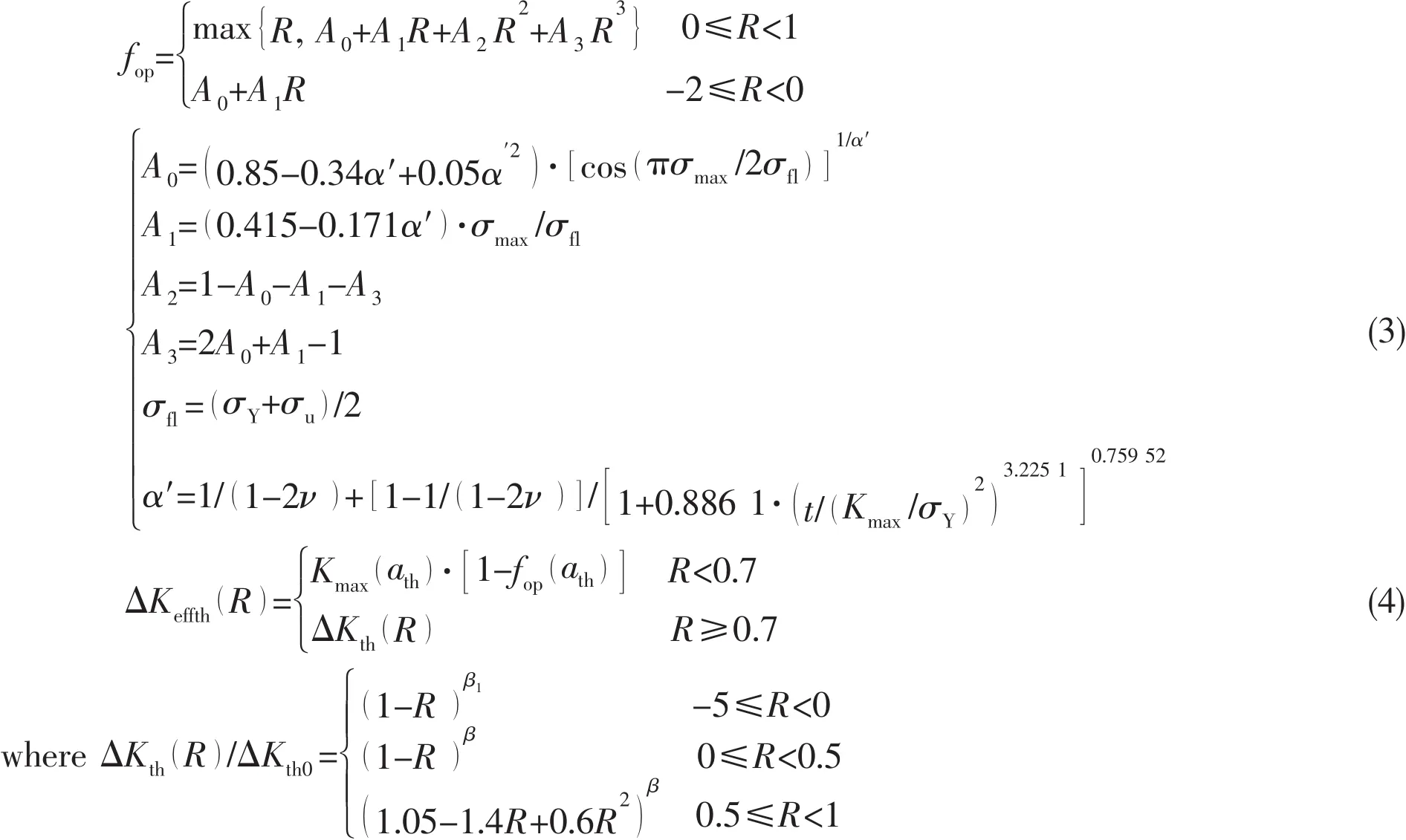
where A is a material-and environmentally-sensitive constant of dimensions(MPa)-2;m is a constant representing the slope of the corresponding fatigue crack growth rate curve;n is the index indicating the unstable fracture;KICis the plane strain fracture toughness of the material;KCfis the fracture toughness of the material under fatigue loading;reis an empirical material constant of the inherent flaw length of the order of 1 μm;a is the modified crack length which is equal to replus the actual crack length;σmaxis the maximum applied stress,σminis the minimum applied stress;Y(a)is a geometrical factor;Y(re)is a geometrical factor when a is equal to re;R is the stress ratio(=σmin/σmax);ΔKthis the threshold value of stress intensity factor range;ath is the threshold value corresponding to ΔKth;ΔKeffis the effective range of the stress intensity factor;ΔKeffthis the effective range of the stress intensity factor at the threshold level;Kopis the stress intensity factor at the opening level;α′is the crack tip stress/strain constraint ratio,which is 1 for the plane stress state and 1/(1-2v)for the plane strain state. The effect of n is significant only in the unstable propagation region;a constant value of 6 is recommended for a quick and simple engineering analysis.Eq.(4)can be used to determine the value of ΔKeffthand we recommend the values of β and β1are 0.4 and 0.36 respectively for titanium alloys.But the prediction error in the unstable region reflects the inaccuracy of the assumption of KCf=KIC.

In considering overload effect,it is assuming that the single overload effect is due to variations in crack closure stress in metals and the large plastic zone as a result of overloading can raise the stress intensity factor at the opening level.A large plastic zone is created as a re-sult of an overload,and the crack closure level instantaneously rises to the maximum value, and then gradually recovers to the initial level under constant amplitude loading when the crack penetrates the large plastic zone in the subsequent cycles.A modified coefficient,Φ,on the basis of Wheeler model has been introduced as a magnification factor to correct the amount of the stress intensity factor at crack opening level during the recovering period after an overload in the improved constitutive model illustrated in Fig.5.

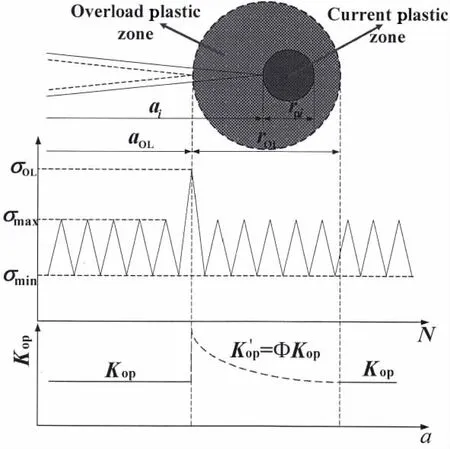
Fig.5 Schematic representation of the assumed change of Kopunder load sequence with single overloading

To account for the change of the crack closure level,a coefficient,Φ,is introduced in the improved constitutive model,

Then it is important to estimate the plastic zone size in front of the crack tip first.Liu et al[6]proposed an equation to calculate the plastic zone size in front of the crack tip as follows:

The plastic zone size mentioned above is also called monotonic plastic zone,which can be used to calculate the plastic zone due to one overload.As the minimum cyclic load in a cycle is approached,yielding in compression occurs in a region of a smaller size,called the cyclic plastic zone,as expressed in Eq.(7)[7]:

Suppose that the single tensile overload and a short period of holding time will not induce crack propagation but just result in a monotonic plastic zone.Based on the assumption, Fig.6 is proposed to illustrate the plastic zone distribution due to the cyclic loading with overload dwell time.Among them,rdtis defined as the plastic zone increment due to dwell time. Then the total monotonic plastic zone can be expressed as the assumption of rOLand rdt.And Eq.(5)will be modified to,

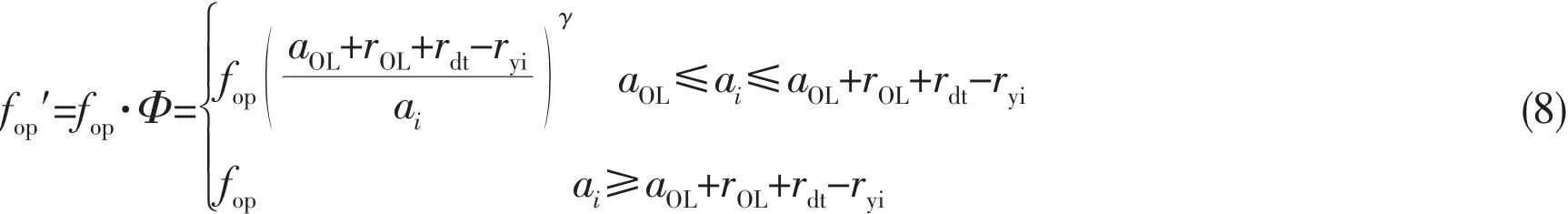
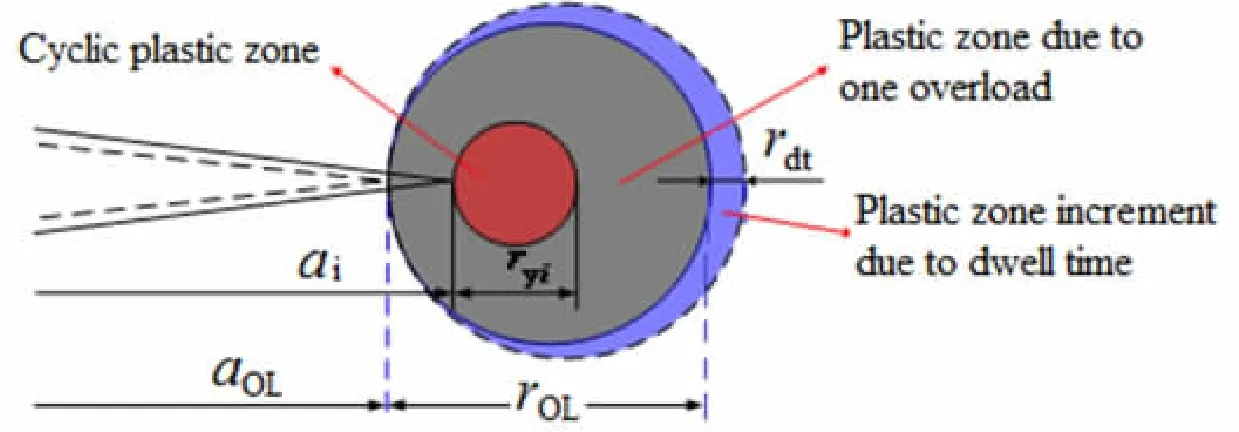
Fig.6 Schematic representation of the plastic zone due to cyclic loading with overloaded dwell time

The physical mechanisms causing creep differ markedly for different classes of materials. In addition,even for a given material,different mechanisms act at various combinations of stress and temperature[8].During low temperature creep(＜0.25Tm)of many metals and alloys,primary creep is the dominant deformation mode.At low creep stresses and creep strains(＜2×10-3), the primary creep deformation of many metals and alloys has been described by a logarithmic creep law of the form ε=llnt+C.In cases where there is larger accumulation of primary creep strains,the deformation can be often described by a power law function of creep strain with time,

where C and k are constants.And the dimension of T is second.

According to the Ramberg-Osgood stress-strain curve,

Creep deformation due to creep in room temperature is plastic

deformation.And if thecreep strain is equivalent to the value due to monotonic stress σcreep,then the stress can be expressed as,

Then the monotonic plastic zone can be simply modified to the following equation,

where KOLCresults from the combined effects of an instant overload and the load holding time T,which can be expressed as follows:

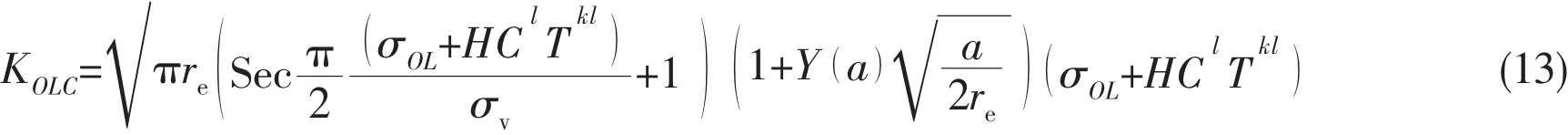
The above equation can be used to calculate the assumption of rOLand rdtduring the overload dwell time as follows:

Then,the crack growth rate for the load pattern of Fig.4(b)can be calculated by combining E-qs.(2),(8)and(14).

3 Example

An example for a candidate titanium alloys used for deep manned submersibles,TC4 ELI will be used to show the application of the proposed model.The chemical compositions of the present tested sample of TC4 ELI,is given in Tab.1.Its tensile test results will not specifically illustrated here,which can be referred to Wang et al[9]Normal crack growth and creep tests are conducted first to obtain the room temperature creep parameters.All crack growth test specimens were conducted using a MTS810 servo-hydraulic testing machine.Standard C-T specimens with dimensions of B=12.5 mm;W=50 mm were cut and machined from three layers of 90 mm-thick hot rolled thick plate at three load ratios,i.e.0.0,0.5,0.8 to obtain date over a wide range of growth rates, with 2 specimens under each stress level,respectively from two sampling directions,parallel to rolling direction and vertical to rolling direction.Crack growth test results can be shown in Fig.7 together with the prediction curves using the unified crack growth rate model.

Fig.7 Crack growth test results of TC4 ELI specimens

Tab.1 Chemical composition of TC4 ELI(wt.%)

Standard specimens were prepared for room temperature creep testing.The force is to be held constant for 84 hours.The creep strain or deformation is measured with time and the time rupture is recorded if this occurs during the test.The creep behavior for one specimen can be observed on a graph of displacement versus time as shown in Fig.8.There is an initial nearly instantaneous occurrence of elastic and perhaps also plastic deformation(or strain)followed by accumulation of creep deformation(or strain).Then the deformation rate d(Δl)/dt,hence the slope of the Δl versus t plot,is at first relatively high.However,the rate decreases and becomes approximately constant with time increasing.

Fig.8 Normal creep test results of TC4 ELI

Fig.9 Total results of creep strain versus time curves for normal creep of TC4 ELI

Fig.9 gives the total results of creep strain versus time curves for normal creep of TC4 ELI. A relatively large scatter is observed comparing results for different specimens,which may result from different position and direction of the specimens as well as some discrepancy of microstructures of the specimens.The most conservative curve can be chosen for life analysis.Thenthe power law function of creep strain with time for TC4 ELI can be expressed as follows:

Then all of parameters used in the crack growth models and creep models can be obtained together with tensile test results of the material,which are listed in Tab.2.Based on that,the crack length versus cycles curve under cyclic load pattern with one overload and a single dwell overload(10 minutes)can be obtained using the proposed model,as shown in Fig.10.It can be seen that retardation will occur under the effect of overload and a period of dwell time.It is from the compressive plastic zone in the vicinity of the crack tip.

Tab.2 Parameters of crack growth rate model and creep model for Ti6Al4V ELI(R=0.1)

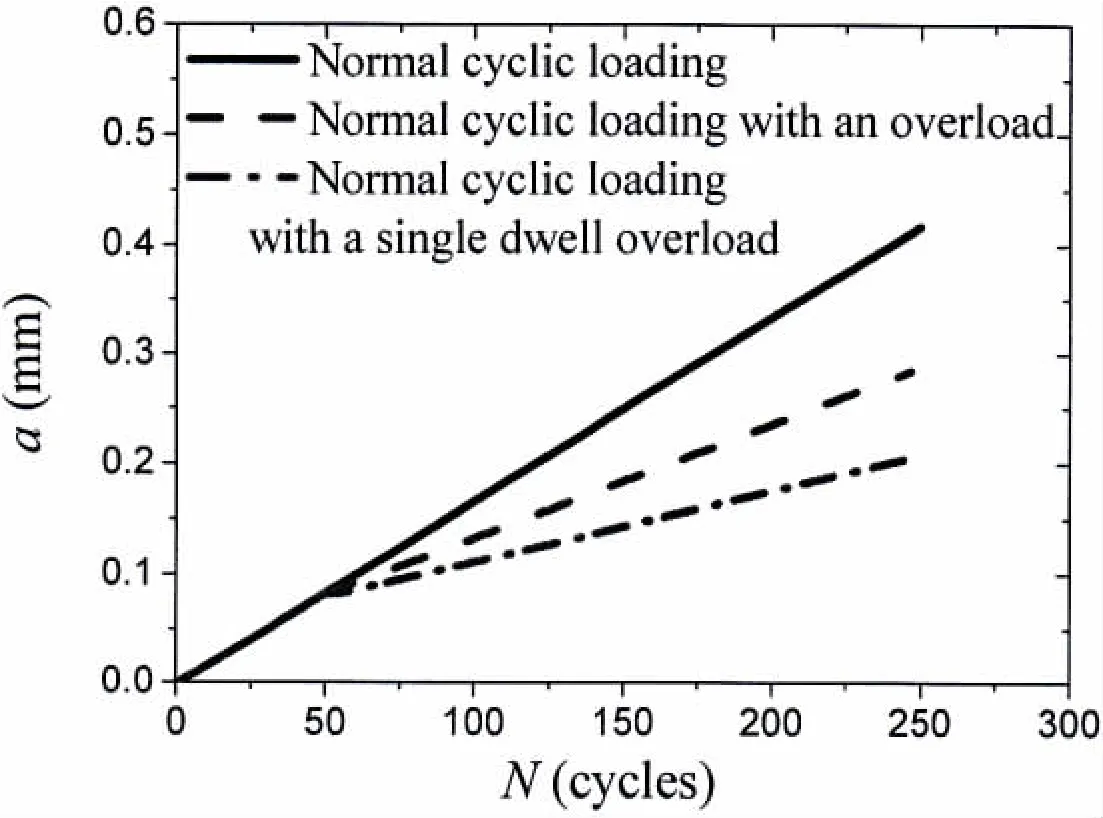
Fig.10 Crack length versus cycles curve under cyclic load pattern with a single dwell overload(10 minutes)

4 Summary and conclusions

In this paper,a new prediction model for the load pattern of cyclic loading with a single dwell overload is proposed.The calculation methods of the total monotonic plastic zone size in the vicinity of crack tip,due to the overload and the dwell time are provided and the corre-sponding variation of crack opening level based on the total monotonic plastic zone can be obtained.Tests are conducted to obtain the parameters used in the crack growth models and creep models together with tensile test results of the material TC4 ELI,which is as an example to calculate the retardation effects of overload and dwell time.It is observed that the model can reasonably reflect the retardation effects due to compressive plastic zone in the vicinity of the crack tip induced by dwell time.The model can theoretically explain the retardation phenomenon and validation tests will be conducted in the future’s research.

Acknowledgments

This work is supported by Youth Foundation of Jiangsu Province‘Study on the time-scale crack growth rate model used in fatigue life assessment of pressure hull of deep-sea submersibles’(Project No.BK2012095);Special program for Hadal Science and Technology of Shanghai Ocean University(Project No.HAST-T-2013-01);The doctoral research fund of Shanghai Ocean University(2013-2015).

[1]Munz D,Bachmann V.Effect of hold time and environment on fatigue crack growth rate in Ti alloys[J].Material wissenschaft und Werkstofftechnik,1980,11(5):168-172.

[2]Wakai T,Poussard C,Drubay B.A comparison between Japanese and French A16 defect assessment procedures for creepfatigue crack growth[J].Nuclear Engineering and Design,2003,224(3):245-252.

[3]Zhao J,Mo T,Nie D F,Ren M F,Guo X L,Chen W X.Acceleration and retardation of fatigue crack growth rate due to room temperature creep at crack tip in a 304 stainless steel[J].Journal of Materials Science,2006,41(19):6431-6434.

[4]Cui W,Wang F,Huang X.A unified fatigue life prediction method for marine structures[J].Marine Structures,2011,24 (2):153-181.

[5]Newman J J.A crack opening stress equation for fatigue crack growth[J].International Journal of Fracture,1984,24(4): 131-135.

[6]Liu Q,Wang F,Huang X P,Cui W C.Three dimensional FE analysis of the plastic zone size near the crack tip[J].Journal of Ship Mechanics,2006,10(5):90-99.

[7]Voorwald H J C,Torres M A S,Pinto Júnior C C E.Modelling of fatigue crack growth following overloads[J].International Journal of Fatigue,1991,13(5):423-427.

[8]Dowling N E.Mechanical behavior of materials:engineering methods for deformation,fracture,and fatigue[M].Prentice Hall,1993.

[9]Wang F,Cui W,Pan B,Shen Y,Huang X.Normalised fatigue and fracture properties of candidate titanium alloys used in the pressure hull of deep manned submersibles[J].Ships and Offshore Structures,(ahead-of-print),2013:1-14.

U661.4Document code:A

10.3969/j.issn.1007-7294.2014.09.010

1007-7294（2014）09-1117-12

date：2014-04-23

Supported by Youth Foundation of Jiangsu Province(BK2012095);Special program for Hadal Science and Technology of Shanghai Ocean University(HAST-T-2013-01);The doctoral research fund of Shanghai Ocean University(2013-2015)

Biography：WANG Fang(1979-),female,Associate researcher of Shanghai Ocean University,E-mail: wangfang@shou.edu.cn;CUI Wei-cheng(1963-),male,professor/tutor.