全平面內(nèi)隨機Dirichlet級數(shù)的幾個定理
譚洋
(中國人民大學信息學院,北京100872)
全平面內(nèi)隨機Dirichlet級數(shù)的幾個定理
譚洋
(中國人民大學信息學院,北京100872)
利用Nevanlinna理論研究了全平面內(nèi)隨機Dirichlet級數(shù)所表示的整函數(shù)的增長性和值分布,得到全平面內(nèi)水平帶形上的幾個新的定理,推廣了以往研究半平面內(nèi)水平半帶形上關(guān)于增長性和值分布的一些相關(guān)結(jié)論.
隨機Dirichlet級數(shù);增長級;值分布;Picard點
1 引言
關(guān)于隨機Dirichlet級數(shù)的值分布,國內(nèi)外學者進行了大量的研究,取得了一系列重要成果(參考文獻[1-9]).本文通過對全平面內(nèi)隨機Dirichlet級數(shù)所表示的整函數(shù)的增長性和值分布的研究,得到結(jié)論:對于{Xn(ω)}(n=0,1,2,···)是獨立同分布的隨機Dirichlet級數(shù)在任何水平帶形意義下的a.s.增長性與其在全平面內(nèi)的a.s.增長性相同,對于無窮級隨機Dirichlet級數(shù)a.s.在任何水平帶形的邊界上都存在Picard點.對于{Xn(ω)}(n=0,1,2,···)是獨立非同分布的隨機Dirichlet級數(shù)在一定條件下的a.s.增長性與其在全平面內(nèi)的a.s.增長性相同.
2 預備知識
本文的符號除特別說明外均參考文獻[10-12].
定義2.1設(shè){Xn(ω)}(n=0,1,2,···)是概率空間(?,A,P)上的一個復隨機變量序列,設(shè)非負數(shù)序列{λn}(n=0,1,2,···)滿足:

那么
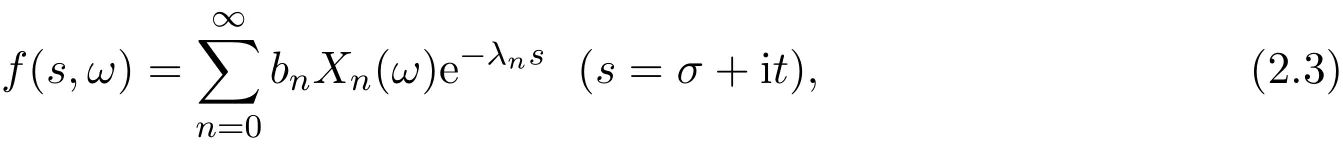
表示全平面內(nèi)的隨機Dirichlet級數(shù),這里σ及t都是實變量.
本文中{Xn(ω)}均為獨立的.為了方便,引入輔助Dirichlet級數(shù).
定義2.2設(shè)級數(shù)

滿足條件(2.1)和(2.2),那么級數(shù)(2.4)表示全平面內(nèi)一個Dirichlet級數(shù),這里σ及t都是實變量.
令

定義2.3Dirichlet級數(shù)f(s)與隨機Dirichlet級數(shù)f(s,ω)的級分別是

引理2.1[11]設(shè)c為一正的常數(shù),x是任一正實數(shù),那么函數(shù)
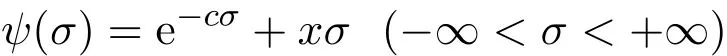
引理2.2[11](Paley-Zygmund)設(shè){Xn(ω)}(n=0,1,2,···)是概率空間上的獨立同分布的隨機變量序列,數(shù)學期望滿足E(Xn)=0,方差滿足E(|Xn|2)=θ2>0,則對任意的H∈A,存在
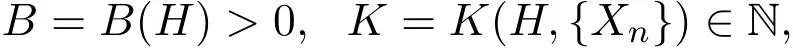
使得對任何復數(shù)列{bn}?C及任何自然數(shù)p與q,p>q≥K,恒有
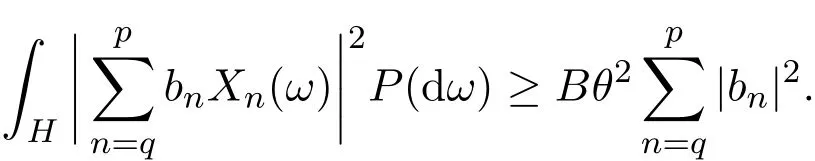
引理2.3[11-12]設(shè)級數(shù)(2.4)滿足條件(2.2),則有下式成立:
引理2.4[11](Paley-Zygmund)設(shè){Xn(ω)}(n=0,1,2,···)是概率空間上的獨立非同分布的隨機變量序列,數(shù)學期望滿足E(Xn)=0,方差滿足則對任意的存在
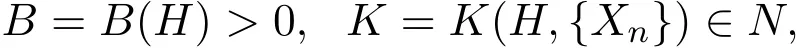
使得對任何復數(shù)列{bn}?C及任何自然數(shù)p與q,p>q≥K恒有
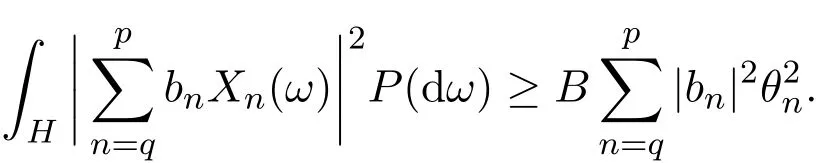
引理2.5[12](Valiron)設(shè)函數(shù)ψ(z)在|z|<1內(nèi)解析,并且成立,其中M(r,ψ)=max{|ψ(z)|:|z|=r<1}.那么在|z|=1上必有一點z0,在它的任何鄰域內(nèi),ψ(z)取任何復數(shù)值無窮多次,至多有一例外值.z0稱為ψ(z)的一個Picard點.
3 主要結(jié)果
定理3.1設(shè)λn及bn滿足條件(2.1)和(2.2),{Xn(ω)}(n=0,1,2,···)是概率空間(?,A,P)上的獨立同分布的隨機變量序列,那么f(s,ω)a.s.具有下列性質(zhì):對任意的實數(shù)α及β(α<β),
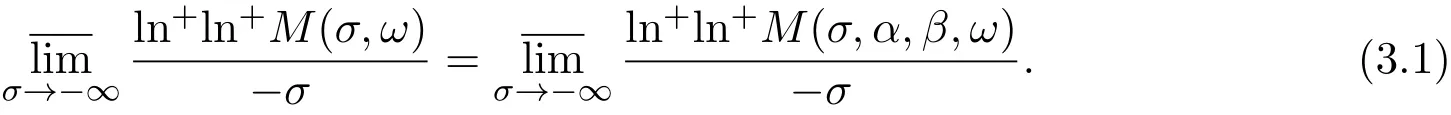
定理3.2設(shè)f(s,ω)為無窮級隨機Dirichlet級數(shù),λn,bn及{Xn(ω)}(n=0,1,2,···)滿足定理3.1中的條件,那么f(s,ω)具有下列性質(zhì):在全平面中任何水平帶形的邊界上一定存在Picard點.
定理3.3設(shè)λn及bn滿足條件(2.1)和(2.2),{Xn(ω)}(n=0,1,2,···)是概率空間上的獨立非同分布的隨機變量序列,滿足:
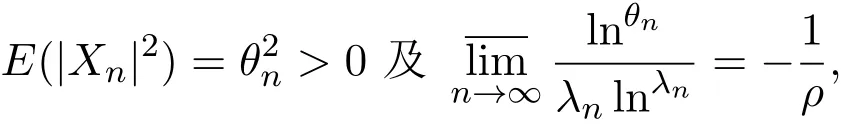
那么f(s,ω)a.s.具有下列性質(zhì):對任意的實數(shù)α及β(α<β)有下式成立:

推論3.1對于滿足定理3.3的條件的非同分布的隨機變量也有定理3.2的結(jié)論.
4 定理的證明
4.1 定理3.1的證明
設(shè)(3.1)式的左邊的上極限等于ρ a.s..當ρ=0時,(3.1)式是顯然成立的.
設(shè)0<ρ≤+∞,假定?中有一概率大于零的事件E,相應的有一個正數(shù)ρ′(<ρ),使得對于ω∈E以及某兩實數(shù)α及β(α<β),有

那么當σ→?∞且α 由引理2.2,對充分大的N,有 所以,當?σ充分大,n≥N時,有 在(4.2)式兩邊同時除以λnlnλn,則有 即 與引理2.3矛盾,所以命題得證. 4.2 定理3.2的證明 假定?中有事件E,P[E]>0對于ω∈E及某一復數(shù)s0=σ0+it0與某一正數(shù)ε(<π),假設(shè)f(s,ω)在水平帶形的邊界上沒有Picard點,假設(shè)水平帶形是以t0為中線寬為2ε的水平帶形,作變換 通過上述變換得到: 令 設(shè) 則可計算出 對于無窮級隨機Dirichlet級數(shù),由級數(shù)的定義,有 由定理3.1,有 則取{σn}→?∞的子列,仍記為{σn},使 取{sn=σn+itn,|tn?t0|<ε,σn∈},使得 又因為 即 若 其中ρ為有限數(shù),則 即 矛盾,所以有 成立.則由引理2.5可知,f(s,ω)在水平帶形的邊界上一定有Picard點,所以假設(shè)不成立,命題成立. 4.3 定理3.3的證明 設(shè)(3.2)式的左邊的上極限等于ρ a.s..當ρ=0時(3.2)式是顯然成立的. 設(shè)0<ρ≤+∞,假定?中有一概率大于零的事件E,相應的有一個正數(shù)ρ′(<ρ),使得對于ω∈E以及某兩個實數(shù)α及β(α<β),有 那么當σ→?∞且α 則有 由引理2.4,對充分大的N,有 所以當?σ充分大,n≥N時,有 在(4.4)式兩邊同時除以λnlnλn,則有 即 則與引理2.3矛盾,所以命題得證. 參考文獻 [1] 余家榮.Dirichlet級數(shù)與隨機Dirichlet級數(shù)在水平直線上的增長性[J].江西師范大學學報,1995,19(3):189-196. [2] 孫道椿,高宗升.無限級隨機Dirichlet級數(shù)的值分布[J].數(shù)學年刊,1993,14:677-685. [3] 孫道椿.半平面上的隨機Dirichlet級數(shù)[J].數(shù)學物理學報,1999,19(1):107-112. [4] 孫道椿,陳特為.無限級Dirichlet級數(shù)[J].數(shù)學學報,2001,44:259-268. [5] 孫道椿.Dirichlet級數(shù)的級[J].華南師范大學學報,2001,3:14-20. [6] 鄧冠鐵.Dirichlet級數(shù)表示的整函數(shù)的增長性[J].北京師范大學學報,2002,38(2):156-159. [7] 劉素紅,田宏根.Dirichlet級數(shù)的增長性[J].純粹數(shù)學與應用數(shù)學,2013,29(3):264-274. [8] 楊樂.值分布及其新研究[M].北京:科學出版社,1982. [9] Tsuji M.Potential Theory in Modern Function Theory[M].Tokyo:Maruzen,1959. [10] 余家榮.隨機狄里克萊級數(shù)的一些性質(zhì)[J].數(shù)學學報,1978,21:97-118. [11] 余家榮,丁曉慶,田范基.Dirichlet級數(shù)與隨機Dirichlet級數(shù)的值分布[M].武漢:武漢大學出版社,2004. [12] 余家榮.狄里克萊級數(shù)與隨機狄里克萊級數(shù)[M].北京:科學出版社,1997. Several theorems of random Dirichlet series Tan Yang By Nevanlinna theory we study the growth and distribution of the entire function expressed by a random Dirichlet series on the whole plane.We get several new theorems in the horizontal strip on the whole plane.We extend some relevant results of the growth and distribution of the entire function expressed by a random Dirichlet series in the half horizontal strip on the half plane. random Dirichlet series,the growth,the value distribution,Picard points O178 A 1008-5513(2014)05-0512-08 10.3969/j.issn.1008-5513.2014.05.013 2014-04-27. 國家自然科學基金(11171013). 譚洋(1979-),博士生,研究方向:函數(shù)論. 2010 MSC:30D30
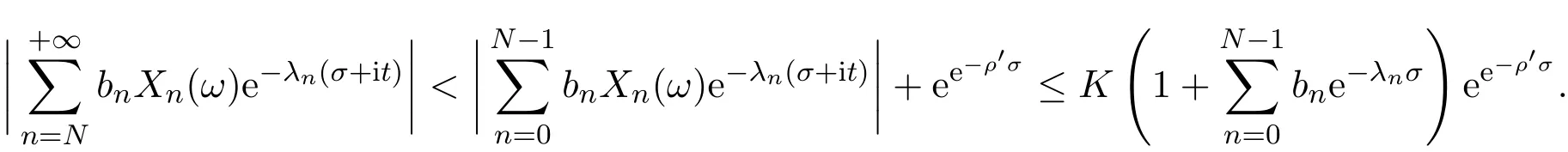


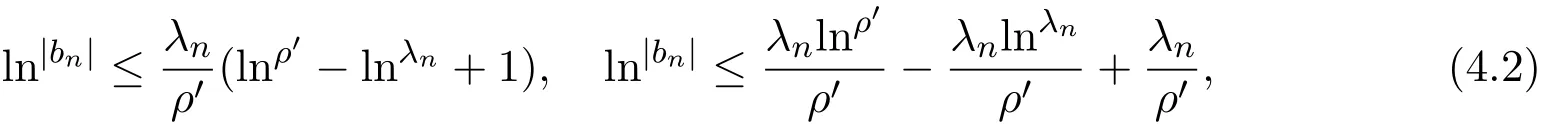


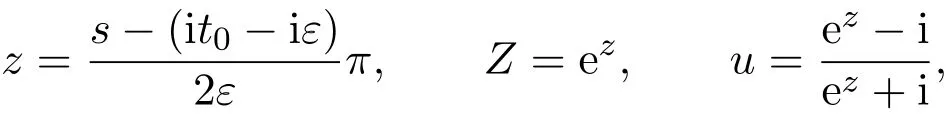
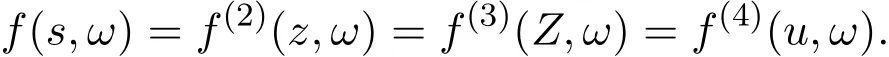


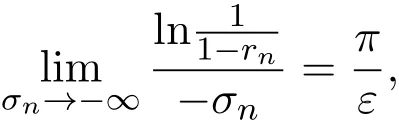







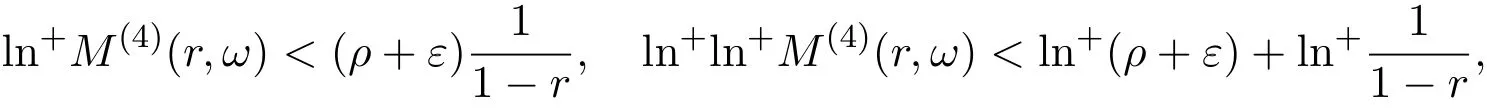
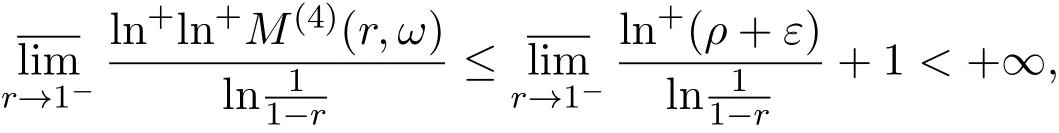
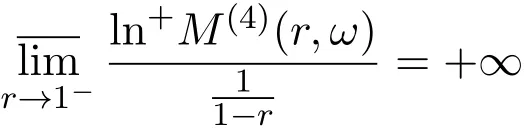
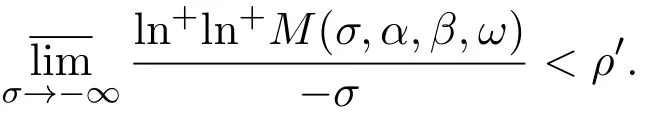
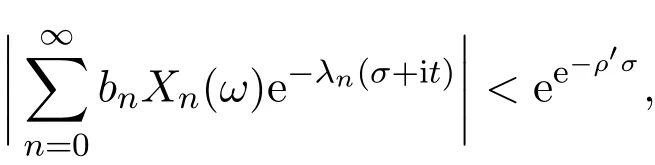


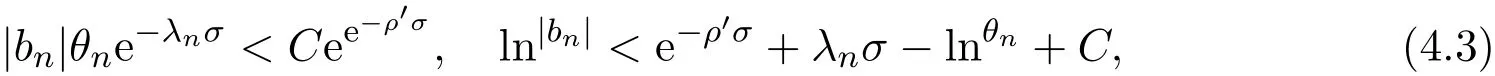


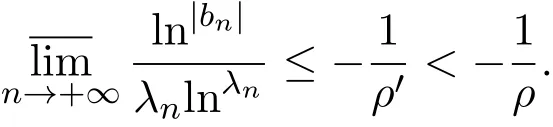
(School of Information,Renmin University of China,Beijing100872,China)

