Outer P(ρ,σ)-set’s Random Characteristic and Application
ZHANG Huan-li,WANG Dong-mei
(1.School of Mathematics,Shandong University,Jinan 250100,China;2.Department of Information Engineering,Zhumadian Vocational Technology College,Zhumadian 463000,China)
Outer P(ρ,σ)-set’s Random Characteristic and Application
ZHANG Huan-li1,2,WANG Dong-mei2
(1.School of Mathematics,Shandong University,Jinan 250100,China;2.Department of Information Engineering,Zhumadian Vocational Technology College,Zhumadian 463000,China)
Based on the conception of P(ρ,σ)-set(XρPFˉ,XσPF),this paper studied the relation between outer P(ρ,σ)-set and outer P-set:give outer P(ρ,σ)-set and outer P-set relation theorem,outer P(ρ,σ)-set and numerical value σ relation theorem,outer P(ρ,σ)-set’s range; studied other characteristics of outer P(ρ,σ)-set:give the fi niteness theorem of outer P(ρ,σ)-set,the set chain theorem of outer P(ρ,σ)-set,the outer P(ρ,σ)-set probability interval fi nite partition theorem,and its corollary;also give generation,reduction,identi fi cation theorem of outer P(ρ,σ)-set, fi lter generation theorem of outer P(ρ,σ)-set; fi nally give its application.
P-set;outer P(ρ,σ)-set; fi niteness; fi nite partition;probability
§1.Introduction
In 2008,[1]embedded the dynamic characteristic into the Cantor set,proposed P-set,the dynamic characteristic of P-set is realized by element transfer.?x∈X,ˉf(x)=uˉ∈X;?u∈U,uˉ∈X,f(u)=x0∈X.The former shows that element x in set X is transferred out of set X under the function of transferˉf∈ˉF,the elements left form internal P-set XˉF;The latter shows element u out of set X is transferred into set X under the function of element transfer f∈F,the elements in set X and transferred into set X form outer P-set XFtogether;P-set is a set-pair composed of internal P-set XˉFand outer P-set XF,or(XˉF,XF)is P-sets.More characteristics and applications of P-set can be seen in[3-15].
In 2010,[2]embedded the random characteristic into P-set,proposed P(ρ,σ)-set,the random characteristic of P(ρ,σ)-set is also realized by element transfer.?x∈X,PFˉ(fˉ(x)=u∈ˉX);?u∈U,u∈ˉX,PF(f(u)=x0∈X).The former shows the probability of element x in set X transferring out of set X under the function of transferfˉ∈Fˉ.The latter shows the probability of element u out of set X transferring into set X under the function of element transfer f∈F. If we stipulate that elements whose emigration probability is equal to or bigger than certain value ρ are all transferred out of set X,the elements left in X form internal P(ρ,σ)-set XρPFˉ; If we stipulate that elements whose immigration probability is equal to or bigger than certain value σ are all transferred into set X,the elements transferred into and X form outer P(ρ,σ)-settogether;P(ρ,σ)-set is a set-pair composed of internal P(ρ,σ)-set XρPFˉand outer P(ρ,σ)-set
Obviously,when PFˉ(fˉ(x)=u∈ˉX)=1,X turns intowhen PF(f(u)=x0∈X)=1, X turns into XF;so P-set(XFˉ,XF)is the special case of P(ρ,σ)-set(),P(ρ,σ)-set (,)is the general form of P-set(XFˉ,XF),P(ρ,σ)-set has better application prospect and bigger application space.
Based on[2],this paper studied the relation between outer P(ρ,σ)-set and outer P-set: give outer P(ρ,σ)-set and outer P-set relation theorem,outer P(ρ,σ)-set and numerical value σ relation theorem,outer P(ρ,σ)-set’s range;studied other characteristics of outer P(ρ,σ)-set: give the fi niteness theorem of outer P(ρ,σ)-set,the outer P(ρ,σ)-set probability interval fi nite partition theorem,the chain theorem of outer P(ρ,σ)-set,outer P(ρ,σ)-set and its attribute set relation theorem,and its corollary;also give generation,reduction,identi fi cation theorem of outer P(ρ,σ)-set, fi lter generation theorem of outer P(ρ,σ)-set; fi nally give its application.
To make it easier for readers to understand this paper,we provide P(ρ,σ)-set and its structure in the second section.
§2.P(ρ,σ)-set and Its Structure
ConventionU is nonempty fi nite element domain;V is nonempty fi nite attribute domain,F={f1,f2,···,fλ}andFˉ={fˉ1,fˉ2,···,fˉr}are element transfer family,f∈F,fˉ∈Fˉ are element transfer;IDE=identi fi cation,UNI=unidenti fi cation,card=cardinal number.
De fi nition 1Let U be a fi nite element domain,set X={x1,x2,···,xm}?U,the probability of?x∈X,fˉ(x)=u ∈X is called the probability of element transferfˉ,written as PFˉ(fˉ(x)=u ∈X)=ρ,shorten as PFˉ(fˉ)=ρ,ρ∈[0,1].
De fi nition 2Let U be a fi nite element domain,set X={x1,x2,···,xm}?U,the probability of u∈U,u ∈X,f(u)=x0∈X is called the probability of element transfer f, written as PF(f(u)=x0∈U)=σ,shorten as PF(f)=σ,σ∈[0,1].



In it,β∈V,β∈α,f∈F the probability of turning β into f(β)=α0∈α is bigger than or equal to/=?.

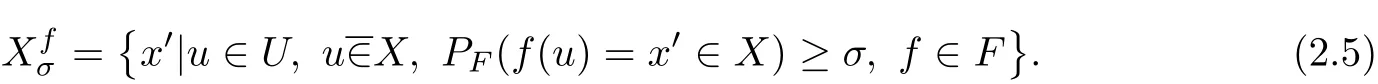

De fi nation 5The set pair composed of internal P(ρ,σ)-set()and outer P(ρ,σ)-setis called P(ρ,σ)-set of X,or

is P(ρ,σ)-set.


From de fi nition 1-de fi nation 6,we can directly get.

Proposition 2If PFˉ(fˉ)and PF(f)exist,P(ρ,σ)-set(,)of set X is the general case of P-set(XFˉ,XF),while P-set(XFˉ,XF)is the special case of P(ρ,σ)-set(.
§3.The Relation Between Outer P(ρ,σ)-set and Outer P-set
Theorem 1(Relation Theorem between Outer P(ρ,σ)-set and Outer P-set)If outer P(ρ,σ)-set XσPF,outer P-set XF,then

Proposition 3If outer P(ρ,σ)-set,element domain U,then

Proof process is similar to Theorem 1.
From Theorem 1 and Proposition 3,we can get
Proposition 4outer P-set XF,element domain U can be seen as two special outer P(ρ,σ)-set.
Theorem 2(Relation Theorem between Outer P(ρ,σ)-setand Numerical Value σ)If,are any two outer-P(ρ,σ)set,in it 0≤σ1<σ2≤1,then

Theorem 3(Range of Outer P(ρ,σ)-set)If outer P(ρ,σ)-setouter P-set XF,element domain U,then XσPFsatisfy

Explanation of Outer P(ρ,σ)-setOuter P(ρ,σ)-setis got by continuing to immigrate elements out of outer P-set XFinto it.
§4.The Characteristics of Outer P(ρ,σ)-set
Def i nition 7Name

outer P(ρ,σ)-set family,if for any σ∈[0,1],there is ais outer P(ρ,σ)-set.
De fi nition 8Name'Ii|i={1,2,···,n},n∈N+“the fi nite partition of probability interval[0,1∩],if it satis fi esthe following conditions.1)For any i1,i2∈{1,2,···,n},i1/=i2there is Ii1Ii2=?;2)=[0,1].In it,Ii(i∈{1,2,···,n})is an interval which belongs to[0,1],called subinterval of[0,1].
Theorem 4(Finiteness Theorem of Outer P(ρ,σ)-set)In outer P(ρ,σ)-set family{|σ∈[0,1]},there is only a fi nite number of outer P(ρ,σ)-set,or outer P(ρ,σ)-set family{|σ∈[0,1]} is a fi nite set.
Theorem 4 is the fact that clearly,prove slightly.
Theorem 5(Chain Theorem of Outer P(ρ,σ)-set)In outer P(ρ,σ)-set family{|σ∈[0,1]},there must be an outer P(ρ,σ)-set chain and it satisfy

In it,0≤σ0<σ1<σ2<···<σq?1<σq≤1,q∈N+;=U,=XF.
ProofAccording to Theorem 4 we can know outer P(ρ,σ)-set family{|σ∈[0,1]}is a fi nite set and for any two,∈{|σ∈[0,1]},if σi/=σj,let σi<σj,get from(3.3)?if σi=σj,get from(2.4)and(2.5)=;thus,in{|σ∈[0,1]}there must be an outer P(ρ,σ)-set chain,that is to say(4.2)is valid;Theorem 5 is proven.
Corollary 1The equivalent form of outer P(ρ,σ)-set family

Theorem 6(Outer P(ρ',σ)-set Probability Interval F“inite Partition Theorem)For outer P(ρ,σ)-set family A=|i∈{0,1,2,··,q},q∈N+,there must be a fi nite partition of interval[0,1]B='Ii|i∈{0,1,2,···,q},q∈N+“,which can make a one-to-one correspondence between A and B.
The process of proof is similar to Theorem 4,prove slightly.
Corollary 2For outer P(ρ,σ)-set family A='|i∈{0,1,2,···,q},q∈N+“,the correspondent probability interval fi nite partition B=Ii|i∈{0,1,2,···,q},q∈N+“,then it satis fi esfor any σ∈Ii∈B,there is=(i∈{0,1,2,···,q},q∈N+).
Theorem 6 and its corollary give a fact.
Corollary 3When σ is in the subinterval of interval[0,1]partition,outer P(ρ,σ)-set Xremains the same.
Theorem 7In outer P(ρ,σ)-set family{|σ∈[0,1]},the following two formulas are valid

Theorem 8(Outer P(ρ,σ)-set and Its Attribute Set Relation Theorem)If the attribute set of outerrespectively∈[0,1]), then

Corollary 4If the attribute set of outerrespectively,then

§5.The Generation and Reduction of Outer P(ρ,σ)-set
Theorem 9(Generation Theorem of Outer P(ρ,σ)-set)If the attribute set of outer-setis,then the necessary and sufficient condition for generating outer P(ρ,σ)-setis that delete the attribute set

from the attribute set α of set X.
In it,αi∈α,fˉ∈Fˉ turns αiinto f(αi)=βi∈α.
ProofThe attribute set of set X is α,the attribute set of outer P-setis
(ρ,σ)and=α?{αi|PFˉ(fˉ(αi)=βi∈α)≥σ0,fˉ∈Fˉ};1)If X generates outer P(ρ,σ)-set,the attribute set α of X turns into the attribute setof,thus we get that in the attribute set α of X it deletes the attribute set{αi|PFˉ(fˉ(αi)=βi∈α)≥σ0,fˉ∈Fˉ}.2)If we delete the attribute set{αi|PFˉ(fˉ(αi)=βi∈α)≥σ0,fˉ∈Fˉ}from the attribute set α of X,the attribute set of X becomes α?{αi|PFˉ(fˉ(αi)=βi∈α)≥σ0,fˉ∈Fˉ},which is just the attribute setof;Therefore X generates outer P(ρ,σ)-set.Get from 1)and 2)Theorem 9.
Corollary 5The necessary and sufficient condition for X generating outer P-set XFis that delete the attribute set

from the attribute set α of set X.
In it,αi∈α,fˉ∈Fˉ turns αiinto f(αi)=βi∈α.
Theorem 10(Reduction Theorem of Outer P(ρ,σ)-set)If the attribute set of outer P(ρ,σ)-setisthe attribute set of set X is α,the necessary and sufficient condition for outer P(ρ,σ)-setreducing to X is

It is easily proved by Def i nition 4.
§6.The Identif i cation and Filter of Outer P(ρ,σ)-set
Theorem 11(Identi fi cation Theorem of Outer P(ρ,σ)-set)Ifandare all outer P(ρ,σ)-set,then the necessary and sufficient condition of IDE{,}is that σ1,σ1belong to di ff erent Ii.
In it,Ii∈B,B='Ii|i∈{0,1,2,···,q},q∈N+“.
Corollary 6(Unidenti fi cation Theorem of Outer P(ρ,σ)-set)Ifandare all outer P(ρ,σ)-set,then the necessary and sufficient condition of UNI{,}is that σ1,σ2belong to one Ii.
In it,Ii∈B,B='Ii|i∈{0,1,2,···,q},q∈N+“.
Theorem 11 and Corollary 6 are easily proved by Theorem 6 and its corollary.
Filter Generation Theorem of Outer P(ρ,σ)-setFor set X={x1,x2,···, xm}?U,under the function of element transfer f,let element u which is out of set X take the given threshold σ,out of X let the element whose transfer probability PF(f)is smaller than σ be fi ltered,bigger than or equal to σ be left,then the elements left and X make up outer P(ρ,σ)-settogether.
§7.The Application of Outer P(ρ,σ)-set in Information System
This case comes from certain domestic import and export corporation,according to the corporation’s annual report,we can get the export probability of various products in 2009 and 2010,and make Table 1 and Table 2 respectively.

Tab 1A Group Company 2009 Annual Probability Distribution of Various Kinds of Products Exports

Tab 2A Group Company 2010 Annual Probability Distribution of Various Kinds of Products Exports
Instance specif i cationIn 2009,because of the explosion of global monetary crisis, export environment worsen,the probability of various export restriction elements(export attribution)rose,and the probability of products export declined,only three products x1,x6,x8export(based on experience,let σ=0.9 be threshold value:the product whose σ≥0.9 is allowed to be exported,while the product whose σ<0.9 is not allowed),the set of export products is X={x1,x6,x8},the attribute set is α={α1,α2,α3,α4,α5}(the name of xi,αjis omitted,it doesn’t inf l uence problem analysis(i=1,2,···,10,j=1,2,···,5)). With the recession of monetary crisis,international export market environment was improved in 2010,various kinds of export attribution probability declined,product export probability rose,therefore the probabilities of export attribution α2,α4are smaller than threshold(that is to say α2,α4are transferred out of α),the attribution set of X changed fromacteristic of outer P(ρ,σ)-set,according to the f i lter generation theorem of outer P(ρ,σ)-set,the following products x1,x3,x4,x6,x7,x8,x9would be exported in 2010,while x2,x5,x10would not be exported.
§8.Discussion
In this case,take the export products set X={x1,x6,x8}in 2009 as basic set,its export attribution set is α={α1,α2,α3,α4,α5},then in 2010 various products make up outer3,4,5 and Corollary 1 are proven);Outer P(ρ,σ)-set family’s corresponding interval[0,1]f i nite partition B={[0,0.80],(0.80,0.82],(0.82,0.85],(0.85,0.90],(0.90,0.91],(0.91,0.93],(0.93,0.94], (0.94,1]},make a one-to-one relationship between A and B(Theorem 6 and corollaries 2,3ability of α2,α4are smaller than threshold value transfer α,X generates outer P(ρ,σ)-set11 and Coyollary 6 is proven);set threshold value σ=0.9,the probabilities of x2,x5,x10are smaller than threshold value and then be f i ltered,the probabilities of x3,x4,x7,x9are{x1,x3,x4,x6,x7,x8,x9}(the f i lter generation theorem of outer P(ρ,σ)-set is proven);The conclusion of this article is proved in the product export report in 2010.
P(ρ,σ)-set is also widely used in real life(hospital discharge,selection competition),in production practice(product test,import and export),and even in the natural biological survival of f i tness,practice has proved,P-set and P(ρ,σ)-set are the most powerful tools for solving the problems of dynamic information system.
[1]SHI Kai-quan.P-sets[J].Journal of Shandong University(Natural Science),2008,43(11):77-84.
[2]YU Xiu-qing.P(ρ,σ)-sets and its random characteristic[J].Computer Science,2010,39(9):218-221.
[3]SHI Kai-quan.P-sets and its application characteristics[J].Computer Science,2010,37(8):1-8.
[4]SHI Kai-quan.P-sets,inverse P-sets and the intelligent fusion-f i lter identif i cation of information[J].Computer Science,2012,39(4):1-13.
[5]SHI Kai-quan.Funtion P-sets[J].Journal of Shandong University(Natural Science),2011,46(2):62-69.
[6]SHI Kai-quan.Function P-sets[J].International Journal of Machine Learning and Cybernetics,2011,2(4): 281-288.
[7]SHI Kai-quan.P-sets and its applications[J].An International Journal Advances in Systems Science and Applications,2009,9(2):209-219.
[8]SHI Kai-quan.P-reasoning and P-reasoning discovery-identif i cation of information[J].Computer Science, 2011,38(7):1-9.
[9]SHI Kai-quan.Inverse P-sets[J].Journal of Shandong University(Natural Science),2012,47(11):98-109.
[10]LIN Hong-kang,Fan Cheng-xian,SHI Kai-quan.Backward P-reasoning and attribution residual discoveryapplication[J].Computer Science,2011,38(10):189-198.
[11]LIN Hong-kang,FAN Cheng-xian.The dual form of P-reasoning and identif i cation of unknown attribute[J]. International Journal of Digital Content Technology and Its Applications,2012,6(1):121-131.
[12]GENG Hong-qin,Zhang Guan-yu,SHI Kai-quan.F-information camouf l age and camouf l age-reduction identif i cation[J].Computer Science,2011,38(2):241-245.
[13]YU Xiu-qing,XU Feng-sheng.P-law reasoning and unknow law discovery-application[J].Journal of Shandong University(Natural Science),2012,47(1):110-115.
tion:03E72
CLC number:O144Document code:A
1002–0462(2014)02–0298–09
date:2013-10-19
Supported by the Basic and Frontier Technology Research Projects of Henan Province (132300410289);Supported by the Natural Science Foundation of Fujian Province(2012D112)
Biography:Zhang Huan-li(1963-),male,native of Xiping,Henan,an associate professor of Zhumadian Vocational Technology College,engages in theory of information system and application.
 Chinese Quarterly Journal of Mathematics2014年2期
Chinese Quarterly Journal of Mathematics2014年2期
- Chinese Quarterly Journal of Mathematics的其它文章
- Some Results of a Certain Odd Perfect Number
- On the Strong Laws for Weighted Sums of m-negatively Associated Random Variables
- Biserial Incidence Algebras
- Bicriteria Scheduling on a Series-Batching Machine to Minimize Makespan and Total Weighted Completion Time with Equal Length Job
- Characterizing C6+P2-graphic Sequences
- Properties for Certain Subclasses of Analytic Functions Associated with Generalized Multiplier Transformation
