Reliability Allocation of Large Mining Excavator Electrical System Based on the Entropy Method with Failure and Maintenance Data
HU Tian-song (胡天松), HUANG Hong-zhong (黃洪鐘), WANG Xiao-ming (王曉明), LI Guang (李 光), GAO Su-he (高素荷)
1 School of Mechanical Electronic and Industrial Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China 2 Taiyuan Heavy Industry Co., Ltd., Taiyuan 030024, China
Reliability Allocation of Large Mining Excavator Electrical System Based on the Entropy Method with Failure and Maintenance Data
HU Tian-song (胡天松)1*, HUANG Hong-zhong (黃洪鐘)1, WANG Xiao-ming (王曉明)2, LI Guang (李 光)2, GAO Su-he (高素荷)2
1SchoolofMechanicalElectronicandIndustrialEngineering,UniversityofElectronicScienceandTechnologyofChina,Chengdu611731,China2TaiyuanHeavyIndustryCo.,Ltd.,Taiyuan030024,China
In the design of large mining excavator electrical system, a practical reliability allocation method was introduced to allocate system level reliability requirements into subsystem and component levels. During the reliability allocation process, factors from the fault and maintenance data were only considered in reliability allocation scheme. It could avoid the disturbance from expert experiences. The entropy method was also used to obtain weights of reliability allocation indexes of large mining excavators considering different factors. Then the failure rate allocation of subsystems and components could be completed.
reliabilityallocation;largeminingexcavators;theentropymethod
Introduction
As a kind of important engineering machineries, the large mining excavator obtains a lot of attentions recently. It is important for the users to enjoy excellent product qualities which should have long service life, low maintenance frequency, and high work efficiency. The reliability allocation can be a powerful method for the above characteristics[1].
Reliability allocation is utilized to improve the system reliability and can affect the competitiveness of product finally[2]. Using reliability allocation, the task reliability index of system is distributed to subsystems according to the allocation method. It is a decomposition process which is from global to local, from large to small, and from top to bottom[3]. Reliability based design optimization problems may be non-deterministic polynomial (NP)-hard[4]. Finding efficient optimization algorithms is one of the most popular research fields[5]. During recent several decades, many researches about the above problem have been done and published[6-9].
However,using reliability allocation, the uncertainties of quantitative weights of influencing factors are not considered efficiently, which mainly come from the expert scorings. The human factors of expert evaluation bring these uncertainties to the reliability allocation. In this paper, we utilize the influencing factors of reliability allocation which comes from the failure data to do the index assignment. Then the weight of allocation indexes can be obtained to complete the reliability allocation based on the entropy method[10-11]finally.
1 Reliability Allocation Model
To utilize the reliability allocation, both the system reliability allocation task index and allocated objects should be known. The reliability allocation model is also needed to be established.
The values of allocation indexes should be determined according to the practical engineering. If the value of index is too small, and the system reliability level is too low, the design solutions can not meet the design requirements. If the value of index is too large, the design solutions may be hard to obtain or will result in high economic price. Therefore, the reliability index values are determined by the system reliability prediction and design experts experience.
For the electrical system of large mining excavator, its reliability function of the system is exponentially distributed, and the mean time between failure (MTBF) is about 100 h. So we can select 200 h as the reliability allocation index of the improved system. Then the improved system reliabilityRs(t) and failure rateλsare shown as
(1)
Based on the analysis of failure mode effects and criticality analysis (FMECA) and failure tree analysis (FTA) of the excavator electric system, we decompose the key system into six subsystems: power system, rectifier and feedback system, (PLC) system, frequency converted driving system, comprehensive monitoring system, and auxiliary system. Considering key subsystems as the reliability allocation objects, (upper and lower control system is not key subsystem, not for reliability allocation) the reliability allocation model is established which is shown in Fig.1.
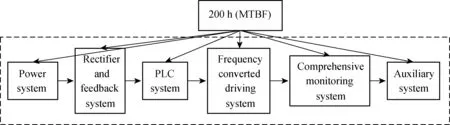
Fig.1 The reliability allocation model of the excavator electrical system
2 Analysis of Failure and Maintainance Data
Here, we use the statistic method to analysis the historical failure and maintenance data. Based on the reliability allocation information from the failure data, two appropriate influencing factors are selected to calculate the allocation weight of electrical subsystems.
1) The failure frequency factor
Itis easy to extract statistic information of the failure frequency of subsystems and components from the actual failure data as the mean time to repair (MTTR). Selecting the failure frequency of subsystems as the basis of distribution, the reliability allocation influencing factor can be obtained as
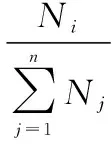
(2)
whereENiis the failure frequency factor of theith subsystem, and if its value is greater, the subsystem failure is more frequent;NiandNjare the failure times of theith and thejth subsystems;Nsis the total failure times of system, which is the sum of subsystems failure times;nis the number of subsystems or components in reliability allocation.
2) The MTTR factor
Selecting the MTTR of subsystems as the basis of distribution, the reliability allocation influencing factor can be obtained as

(3)
whereETiis the MTTR factor of theith subsystem, and if its value is greater, the subsystem MTTR is longer;TiandTjare the MTTR of theith and thejth subsystems;Tsis the total MTTR of system, which is the sum of subsystems MTTR;nis the number of subsystems or components in reliability allocation.
3) The allocation factor calculation
Based on universal criteria of reliability allocation, the reliability allocation factor should be positively correlated because of the failure frequency and MTTR factors. The improvements of reliability and the reductions of failure frequency are needed if the failures of subsystems appear frequently. Thus the allocation factor should be larger. If the MTTR of subsystem is longer, it also needs to reduce its frequency of repair, improve the availability. Thus its allocation factor should be larger.
Series system reliability allocation index is negatively correlated to the allocation factorWias shown in Fig.2. In order to meet the reliability allocation criteria, the reliability allocation factor of series system can be defined respectively as
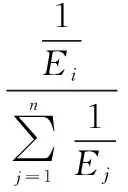
(4)

Fig.2 The reliability allocation model of the series system
whereWiis the allocation factor ofith subsystem;EiandEjare the influencing factors of theith and thejth subsystems, and it can beENiorETi, respectively;nis the number of subsystems or components in reliability allocation.
4) The analysis results
After collecting the excavator failure data during 2012, the failure frequency and MTTR of electrical subsystems can be clearly described in Figs. 3 and 4.
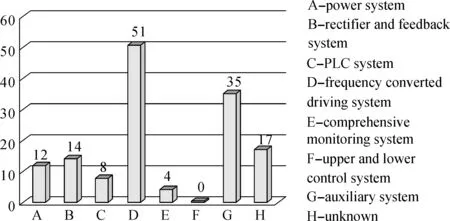
Fig.3 The failure frequency of the excavator electrical subsystems
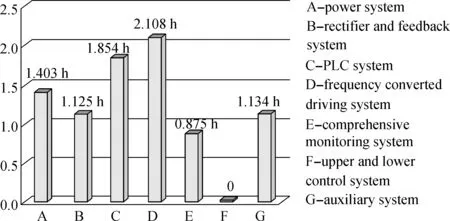
Fig.4 The MTTR of the excavator electrical subsystems
Based on the failure data statistics, the reliability influencing factors of each key subsystem can be obtained using the reliability allocation factor formula of series system in Eq. (4). The values of reliability influencing factors are shown in Tables 1 and 2.
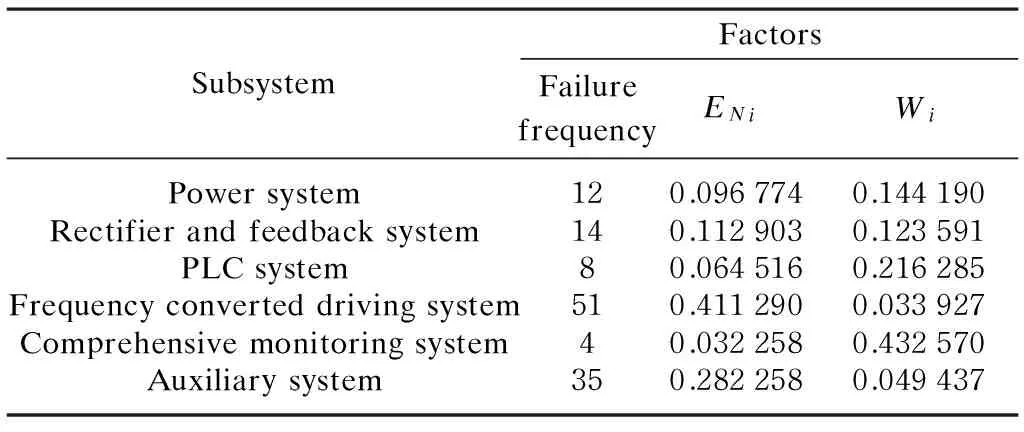
Table 1 The reliability allocation factors based on failure frequency

Table 2 The reliability allocation factors based on MTTR
3 The Reliability Allocation Using the Entropy Method
1) The entropy method
Considering different influencing factors of the failure data, two different allocation factors are used. However, it results in two different allocation results of electrical subsystems. To solve the above problem, entropy method can be used to have the weight transform of two allocation factors.
Information entropy can measure the amount of useful information according to the provided data. On one hand, when the value difference between the evaluating objects on the same indicator is high and the entropy is small, it means that this indicator provides more useful information and the weight of this indicator should be set correspondingly higher. On the other hand, if the difference is smaller and the entropy is higher, the relative weight would be smaller. By calculating the entropy, the best indicators which reflect different dispersion levels among monitoring points can be choosing as the weights.
In the evaluating objectWij, which hasmindicators, the entropy of theith indicator is defined as
(5)

The weight of entropy of thejth indicator could be defined as:
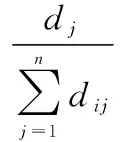
(6)
wheredj=1-Hj.
For reliability allocation factors in Tables 1 and 2, using the entropy method, the new allocation factors are obtained as shown in Table 3.
2) The reliability allocation results
For the electrical system of large mining excavator, its reliability function of the system is exponentially distributed, and MTBF (200 h) is the reliability allocation index. With the reliability allocation factors solved, the electrical subsystems reliability indexes are described as
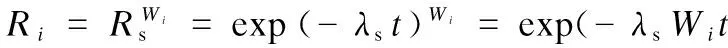
(7)
AndTi(MTBF of each subsystem) can be obtained as
Ti=1/λi=1/λsWi=200/Wi.
(8)
Then the final reliability allocation indexes are shown in Table 4.
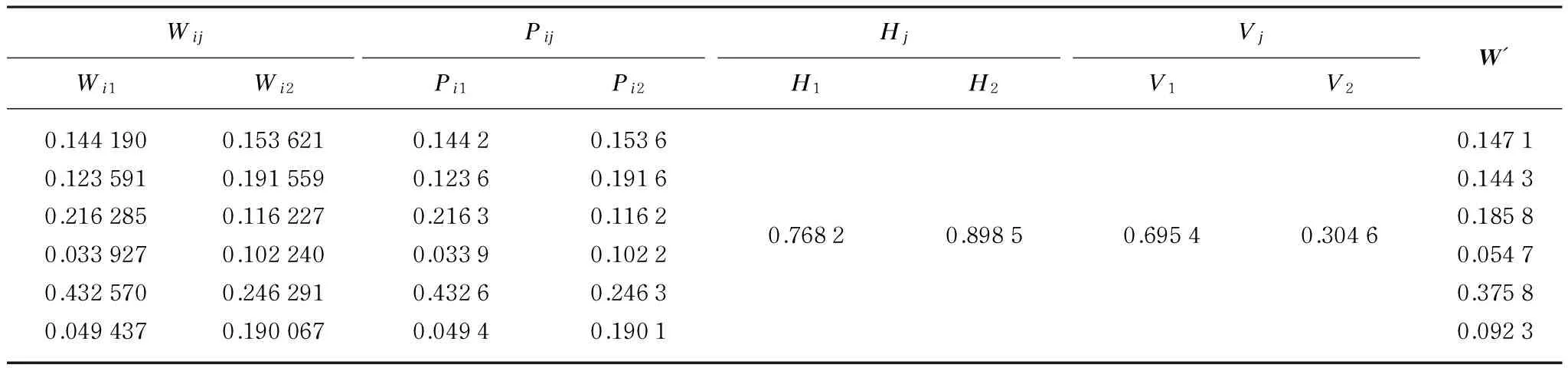
Table 3 The reliability allocation factors using the entropy method

Table 4 The reliability allocation indexes of electrical subsystems
4 Conclusions
The reliability allocation of the electrical system of large mining excavator is important to improve the system reliability. The frequency converted driving system and the auxiliary system are the prior and critical systems for system failure. In this paper, the entropy method is introduced to determine weights of allocation factors, considering two kinds of reliability factors. This method can avoid involving the subjective factor effectively. Thus the allocation results using the entropy method are more reasonable and reliable.
[1] Mettas A. Reliability Aallocation and Optimization for Complex Systems [C]. Proceedings of Annual IEEE of Reliability and Maintainability Symposium, Los Angeles, CA, USA, 2000: 216-221.
[2] Chang Y C, Chang K H, Liaw C S. Innovative Reliability Allocation Using the Maximal Entropy Ordered Weighted Averaging Method [J].Computers&IndustrialEngineering, 2009, 57(4): 1274-1281.
[3] Zhang X G, Wu X Y. Advances in System Reliability Allocation [J].FireControl&CommandControl, 2012, 37(8): 1-4.(in Chinese)
[4] Chen L L, Yu J. Optimal Distribution of Reliability for a Large Network Based on Connectivity [J].AppliedMathematicsandMechanics, 2008, 29(12): 1633-1642.
[5] Zhi W G, Guang B C. Reliability Allocation Using Analytical Target Cascading Method [C]. The 16th International Conference on IEEE Industrial Engineering and Engineering Management, Beijing, China, 2009: 1195-1199.
[6] Berman O, Ashrafi N. Optimization Models for Reliability of Modular Software Systems [J].IEEETransactionsonSoftwareEngineering, 1993, 19(11): 1119-1123.
[7] Zahedi F, Ashrafi N. Software Reliability Allocation Based on Structure, Utility, Price, and Cost [J].IEEETransactionsonSoftwareEngineering, 1991, 17(4): 345-356.
[8] Wang Y Q, Yam R C M, Zuo M J,etal. A Comprehensive Reliability Allocation Method for Design of CNC Lathes [J].ReliabilityEngineering&SystemSafety, 2001, 72(3): 247-252.
[9] Huang H Z. The Fuzzy Method for the Reliability Apportionment of the Mechanical System [J].JournalofMechanicalScienceandTechnology, 1996, 15(2): 182-186.
[10] Xie C, Zhong Z. Entropy Method and Its Application in Comprehensive Evaluation of Bank’s Performance [J].ChinaSoftScience, 2002(9): 108-110.(in Chinese)
[11] Zou Z H, Yun Y, Sun J N. Entropy Method for Determination of Weight of Evaluating Indicators in Fuzzy Synthetic Evaluation for Water Quality Assessment [J].JournalofEnvironmentalSciences, 2006, 18(5): 1020-1023.
Foundation item: National High-Tech Research and Development Program (863 Program), China (No. 2012AA062001)
1672-5220(2014)06-0779-03
Received date: 2014-08-08
* Correspondence should be addressed to HU Tian-song, E-mail: wu235813235813@163.com
CLC number: TB114.3 Document code: A
 Journal of Donghua University(English Edition)2014年6期
Journal of Donghua University(English Edition)2014年6期
- Journal of Donghua University(English Edition)的其它文章
- Optimization of Quality Consistency Problem of Electromechanical Component due to Manufacturing Uncertainties with a Novel Tolerance Design Method
- Effect of Starch Dodecenylsuccinylation on the Adhesion and Film Properties of Dodecenylsuccinylated Starch for Polyester Warp Sizing
- Interval Fault Tree Analysis of Excavator Variable-Frequency Speed Control System
- Combinatorial Optimization Based Analog Circuit Fault Diagnosis with Back Propagation Neural Network
- Deployment Reliability Test and Assessment for Landing Gear of Chang’E-3 Probe
- Reliability Analysis of Hydraulic Transmission Oil Supply System of Power-Shift Steering Transmission with GO Methodology
