On the Laplacian Integral of Tricyclic Graphs?
JING Wei-long,WEN Fei,HUANG Qiong-xiang
(College of Mathematics and System Sciences,Xinjiang University,Urumqi,Xinjiang 830046,China)
Abstract: A graph is a Laplacian integral graph if the Laplacian spectrum consists of integers.In this paper,we find all the Laplacian integer tricyclic base-graphs H with c(H)≤6 where c(H)is the circumference of H.Next we show all the Laplacian integer tricyclic graphs of order n with at least one pendent.Moreover,we show that all the Laplacian integer tricyclic graphs of order n with at least one pendent are determined by their Laplacian spectra.
Key words:Laplacian integral graph;Laplacian spectrum;tricyclic base-graph;tricyclic graph
0 Introduction
LetG=(V,E)be an undirected simple graph withV={v1,v2,...,vn},andE=E(G).LetA(G)be the adjacency matrix ofG,andD(G)be the diagonal matrix whose(i,i)-entry isd(vi).TheLaplacian matrixofGisL(G)=D(G)?A(G).It is well known thatL(G)is positive semide finite so that its eigenvalues can be arranged as follows:
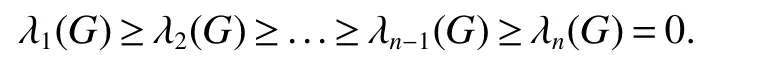
Where λn?1(G)>0 if and only ifGis connected and hence is called the algebraic connectivity ofG.TheLapalcian polynomialofGis de fined as det(λI?L(G)),whereIis the identity matrix.TheLaplacian eigenvaluesofGare the roots of its Laplacian polynomial.TheLaplacian spectrum,denoted byS pecL(G),ofGis a multiset consisting of the Laplacian eigenvalues together with their multiplicities.The length of the longest cycle inG,i.e.thecircumference,is denoted byc(G).
We now introduce some notations and terminology.A graph is called atricyclic graphifHis connected withnvertices andn+2 edges.G∪Hstands for the disjoint union of graphsGandH,andkGstands for the disjoint union ofkcopies ofG.For a graphG,letd(u)denote the degree ofu.Especially,?(G)and δ(G)denote the maximum degree and minimum degree of vertices ofG,respectively.Ifd(u)=1,then we calluapendant vertexofG.As usual,Ks,tdenote the complete bipartite graph withsvertices in one part andtin the other,andCnindicates the cycle of ordern.LetKnandPndenote the complete graph and path of ordern,respectively.Particularly,K1indicates an isolated vertex.
A graph is called aLaplacian integral graphif the spectrum of its Laplacian matrix consists of integers,and a graphGis said to be determined by its Laplacian spectrum if there does not exist other non-isomorphic graphHsuch thatHandGshare the same Laplacian spectrum.
Which graphs have integral spectra?This question was posed in 1973 by F.Hararyand and A.J.Schwenk(see[1]),with the immediate remark that the general problem appears intractable.Indeed,the number of integral graphs is not only in finite,but one can find them in all classes of graphs and among graphs of all orders.However,they are very rare and difficult to be found.But the Laplacian matrices of graphs have received increasing attention in the past 20 years.The readers may be referred to(see[2,3]),and the references therein.Up to now,all the Laplacian integral unicyclic,bicyclic graphs are determined.Moreover,it is proved that all the Laplacian integral unicyclic,bicyclic graphs are determined by their Laplacian spectra(see[4]).In this paper,we characterize all connected Laplacian integral tricyclic base-graphs withc(H)≤6,and we further characterize all the Laplacian integer tricyclic graphs with at least one pendent,and we show that those graphs are determined by their Laplacian spectra.
The organization of this paper is as follows.In Section 2,we give some useful lemmas,they will be used in following section.In Section 3,we characterize all the Laplacian integral tricyclic base-graphs withc(H)≤6.In section 4,we further characterize all connected Laplacian integral tricyclic graphs with at least one pendent,and we show that those graphs are determined by their Laplacian spectra.
1 Elementary
Recently,some results on the Laplacian spectrum have received much attention(see[4],for instance).In this section,now we list some useful lemmas as follows.
Thejoinof two vertex disjoint graphsG1,G2is the graphG1∨G2obtained from their union by including all edges between the vertices inG1and the vertices inG2.
Lemma 1[4]IfGbe a connected graph of ordern(n≥ 2)with at least one pendant vertex,then λn?1(G)≤ 1,where the equality holds if and only ifG=G1∨(K1∪H).
Lemma 2[4]LetTbe a tree of ordern(n≥ 2),thenTis Laplacian integral if and only ifT?K1,n?1.Thus,Tis determined by its Laplacian spectrum if it is Laplacian integral.
Lemma 3[5]LetGbe a graph with at least one edge.Then λ1(G)≥ 4(G)+1.Moreover,ifGis connected,then the equality holds if and only if 4(G)=n?1.
Lemma 4[5][6]IfG1andG2are graphs onkandmvertices respectively,with eigenvalues 0=λk(G1)≤λk?1(G1)≤...≤λ1(G1)and 0=λm(G2)≤ λm?1(G2)≤...≤λ1(G2)respectively,then the Laplacian eigenvalues ofG1∨G2are given by 0,λk?1(G1)+m,...,λ1(G1)+m,λm?1(G2)+k,...,λ1(G2)+k,andm+k.
LetG0=G+edenote the new graph obtained fromGby inserting a new edgeeintoG,andG?ube the new graph yielded fromGby deleting the vertexu∈V(G)and all the edges adjacent tou.
Lemma 5[7]The Laplacian eigenvalues ofGandG0=G+einterlace,that is,
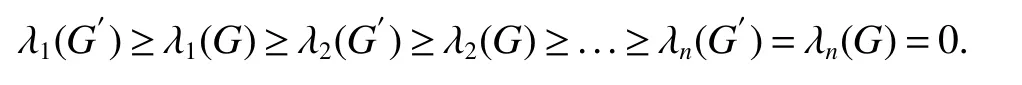
Supposevis a vertex of a connected graphG,ifG?vis disconnected,thenvis called a cutpoint ofG.
Lemma 6[8][12]IfGis a connected graph with a cutpointv,then λn?1(G)≤ 1,where equality holds if and only ifvis adjacent to every vertex ofG.
Lemma 7[9][10]LetGbe a connected graph.Then

wherem(v)=Pd(u)/d(v).Moreover,the equality holds if and only ifGis a regular bipartite graph or bipartite semiregular graph.
2 The Laplacian integral Tricyclic Base-graphs
Let H(3,n)be the set of connected tricyclic graphs.A connected tricyclic graph is said to be atricyclic base-graphif it contains no pendant vertex.We know in[11]that there are exactly fifty type tricyclic base-graphs(see in Figure 1),which are denoted by Hi(i=1,2,...,15)respectively.Clearly there are in finite graphs in Hiand3,n)= ∪i≤15Hi.In addition,eachH∈H(3,n)can be obtained from some graph in Hiby joining some trees.
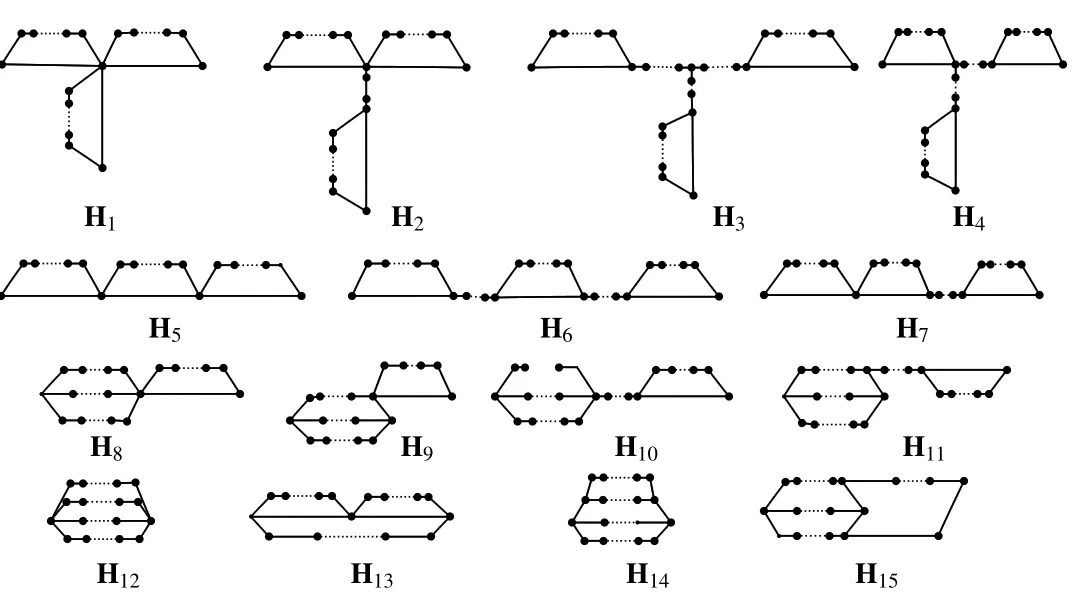
Fig 1 H1?H15
To determine Laplacian integral tricyclic graphs,we firstly need to consider the Laplacian integral tricyclic basegraphs.Let H1={H2,H3,H4,H5,H6,H7,H9,H10,H11}.We observe that each graphHof ordernin H1has a cut pointuwithd(u)= ?(H)

Fig 2 The graphsnd
Lemma 8As shown in Figure 1,all graphs in H1∪{H1,H8}are not Laplacian integrals except ofand
ProofAccording to the above discussions,the possible Laplacian integrals in H1∪{H1,H8}areand.Since=K1∨(3P2),=K1∨(P3∪P2)andP3,P2are Laplacian integral,by Lemma 4andare Laplacian integrals.
According to Lemma 8,to determine the Laplacian integral tricyclic base-graph it suffices to consider the graphs in Hi(i=12,13,14,15).In this section,we mainly get the Laplacian integral tricyclic base-graph of Hiwithc(Hi)≤6(i=12,13,14,15).
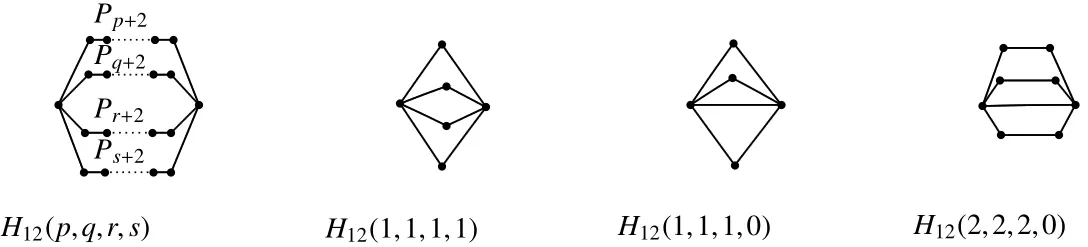
Fig 3 The graphs H12(p,q,r,s),H12(1,1,1,1),H12(1,1,1,0)and H12(2,2,2,0)
Now we label the H12-type graph by identifying initial vertices and terminal vertices of the four vertex-disjoint pathsPp+2,Pq+2,Pr+2,andPs+2,which is denoted byH12(p,q,r,s)and shown in Figure 3.By de finition,p,q,r,s≥0,and it hasn=p+q+r+s+2(≥ 5)vertices andm=n+2(≥ 7)edges sinceH12(p,q,r,s)is a simple graph.
Lemma 9LetH12(p,q,r,s)∈H12be a tricyclic base-graph withc(H12)≤6,thenH12(p,q,r,s)is Laplacian integral if and only if(p,q,r,s)=(1,1,1,1),(1,1,1,0),(2,2,2,0)where the corresponding graphs are shown in Figure3.
ProofBy directcomputation we know thatS pecL(H12(1,1,1,1))=[0,23,4,6],S pecL(H12(1,1,1,0))=[0,22,52],andS pecL(H12(2,2,2,0))=[0,12,2,32,4,6].Hence they are Laplacian integrals.
Next we shall show thatH12(p,q,r,s)is not Laplacian integral if(p,q,r,s),(1,1,1,1),(1,1,1,0),(2,2,2,0).Without loss of generality,assume thatp≥q≥r≥s.We consider the following cases.
Case 1s≥1;
Sinces≥1,wehavep≥q≥r≥1,andso?(H12(p,q,r,s))=4<5≤n?1.ByLemma3,wegetλ1(H12(p,q,r,s))>5.IfH12(p,q,r,s)is a Laplacian integral,then λ1(H12(p,q,r,s))≥ 6.On the other hand,H12(p,q,r,s)is a connected graph,by Lemma 7 we have λ1(H12(p,q,r,s))≤ 6.Thus,λ1(H12(p,q,r,s))=6.Again by Lemma 7,H12(p,q,r,s)is a regular bipartite graph or bipartite semiregular graph.By our assumption,H12(p,q,r,s)is not regular and,it is easily to see thatK2,4=H12(1,1,1,1)is an unique regular bipartite graph in this case,which is a Laplacian integral.
Case 2s=0;
First suppose thatn=p+q+r+s+2≤8.We find all the possible graphsH12(p,q,r,s)in the following Table 1:

Table 1 All the possible Laplacian integrals of H12(p,q,r,0)with c(H12(p,q,r,0))≤6
By simple calculation,we know that the graphsH12(p,q,r,s)in Table 1 are not integral except of(p,q,r,s)=(1,1,1,0),(2,2,2,0).
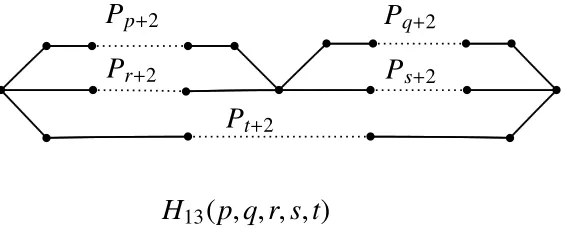
Fig 4 The graph H13(p,q,r,s,t)
Now we label the H13-type graph by identifying initial vertices and terminal vertices of the five vertex-disjoint pathsPp+2,Pq+2,Pr+2,Ps+2andPt+2which areH13(p,q,r,s,t)(see in Figure 4).By de finition,consideringH13(p,q,r,s,t)be a simple graph,we assume thatPp+2andPq+2are not one edge,i.e.p,q≥1.
Lemma 10LetH13(p,q,r,s,t)∈H13be a tricyclic base-graph withc(H13)≤6,thenH13(p,q,r,s,t)is not Laplacian integral.whereH13(p,q,r,s,t)is shown in Figure 4.
ProofWe divide the following three cases.
Case 1r≥1,s≥1;
Since ?(H13(p,q,r,s,t)=4
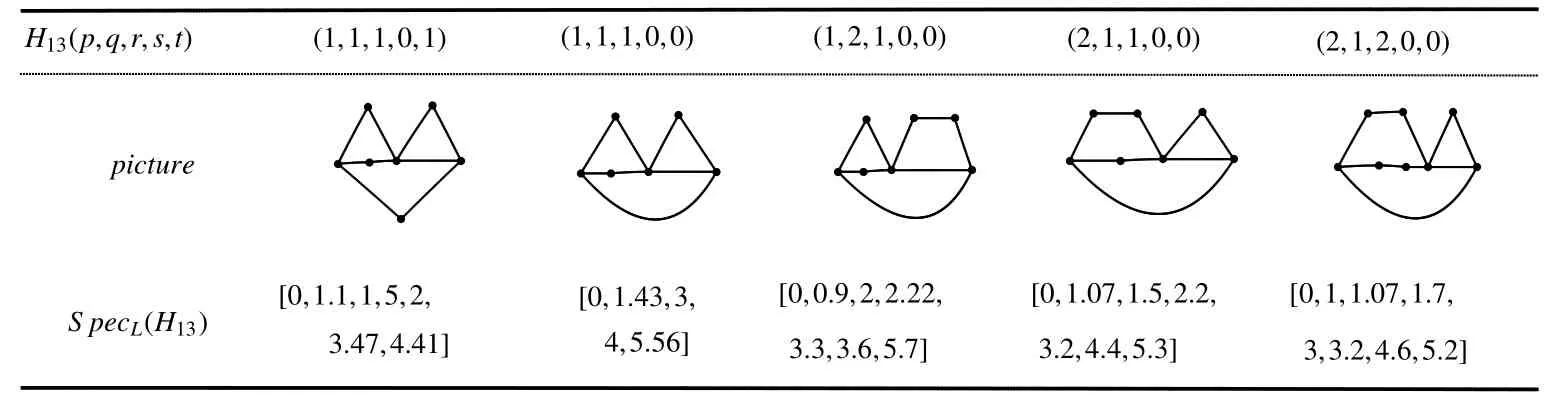
Table 2 All the possible Laplacian integrals of H13(p,q,r≥1,0,t)with c(H13(p,q,r≥1,0,t))≤6
Case 2s=0,r≥1;
H13(p,q,r,s,t)will be the graphs with parameters(p,q,r,s,t)=(1,1,1,0,1),(1,1,1,0,0),(1,2,1,0,0),(2,1,1,0,0),(2,1,2,0,0).We depict these graphs in the Table 2,and by simple calculation we know that they are not Laplacian integral.
Case 3r=s=0;
We depictH13(p,q,r,s,t)will be the graphs with parameters(p,q,r,s,t)=(1,1,0,0,1),(1,1,0,0,0),(1,2,0,0,0),which are not Laplacian integral by simple calculation(see the Table 3).
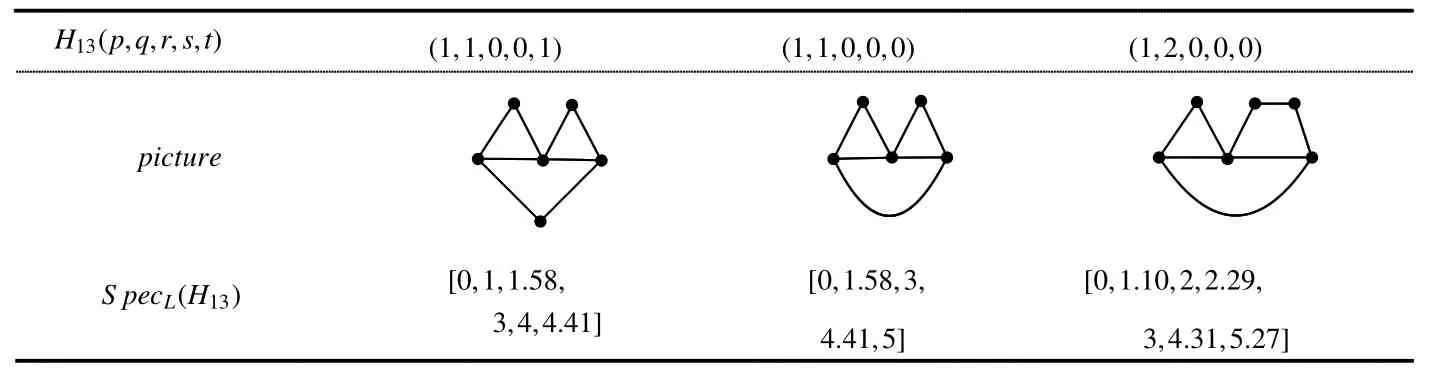
Table 3 All the possible Laplacian integrals of H13(p,q,0,0,t)with c(H13(p,q,0,0,t))≤6
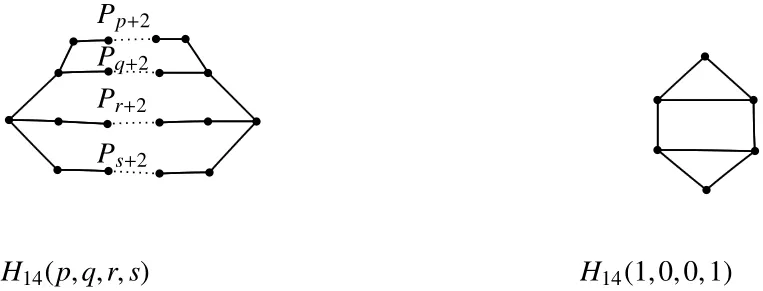
Fig 5 The graphs H14(p,q,r,s)and H14(1,0,0,1)
Next we label the H14-type graph by identifying initial vertices and terminal vertices of the four vertex-disjoint pathsPp+2,Pq+2,Pr+2andPs+2,which areH14(p,q,r,s)and shown in Figure 5.By de finition,consideringH14(p,q,r,s)be a simple graph,we assume thatPp+2andPs+2are not one edge,i.e.p,s≥1.
Lemma 11LetH14(p,q,r,s)∈H14be a tricyclic base-graph withc(H14)≤6,thenH14(p,q,r,s)is Laplacian integral if and only if(p,q,r,s)=(1,0,0,1)where the corresponding graphs are shown in Figure 5.
ProofSincec(H14)≤6,one can easily find that there are only three graphs with parameters(p,q,r,s)=(1,0,0,1),(1,1,0,1),(1,1,1,1)inH14(p,q,r,s).We depict these graphs in the Table 4,and by simple calculation,we know that the graph(p,q,r,s)=(1,0,0,1)is Laplacian integral,but other two are not.
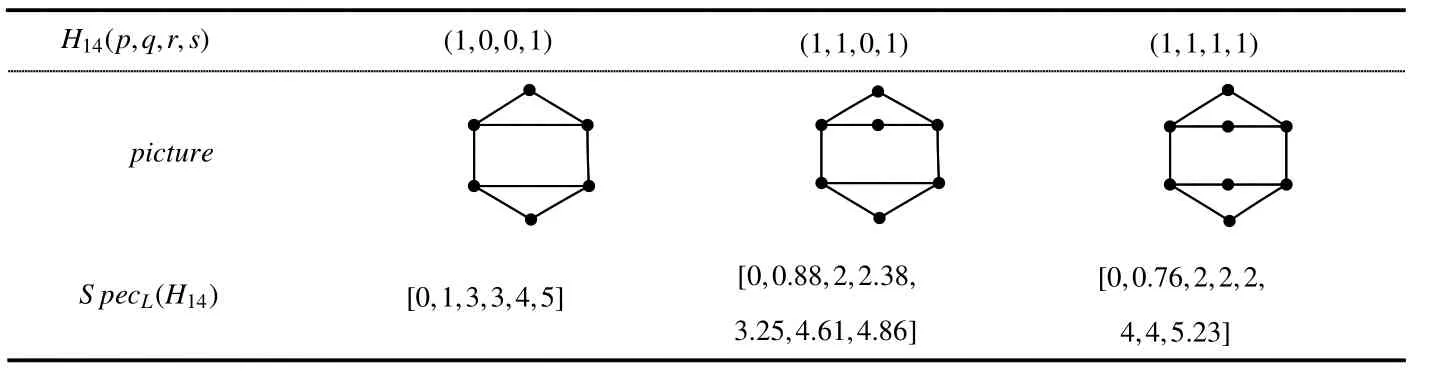
Table 4 All the possible Laplacian integrals of H14(p,q,r,s)with c(H14(p,q,r,s))≤6
Next we label the H15-type graph by identifying initial vertices and terminal vertices of the four vertex-disjoint pathsPp+2,Pq+2,Pr+2,andPs+2,which is denoted byH15(p,q,r,s)and shown in Figure 6.By de finition,p,q,r,s≥0.
Lemma 12LetH15(p,q,r,s)∈H15be a tricyclic base-graph with c(H15)≤6,thenH15(p,q,r,s)is Laplacian integral if and only if(p,q,r,s)=(0,0,0,0),(0,0,0,1)where the corresponding graphs are shown in Figure 6.
ProofWe can simple to find that there are only seven graphs with parameters(p,q,r,s)=(0,0,0,0),(0,0,0,1),(1,0,0,1),(0,1,0,1),(1,0,1,1),(0,0,0,2),(1,1,1,0).We depict these graphs in the Table 5,and by direct calculation,we know that the graphs(p,q,r,s)=(0,0,0,0),(0,0,0,1)are Laplacian integrals,but other five are not.Thus,H15(p,q,r,s)H15(0,0,0,0)orH15(p,q,r,s)H15(0,0,0,1).

Fig 6 The graphs H15(p,q,r,s),H15(0,0,0,0)H15(0,0,0,1)and H0

Table 5 All the possible Laplacian integrals of H15(p,q,r,s)with c(H15(p,q,r,s))≤6
According to Lemma 8-Lemma 12,we are easy to see that.
Theorem 1LetHbe a connected tricyclic base-graph withc(H)≤6,ifHis Laplacian integral,then these graphs are shown in the Table 6.
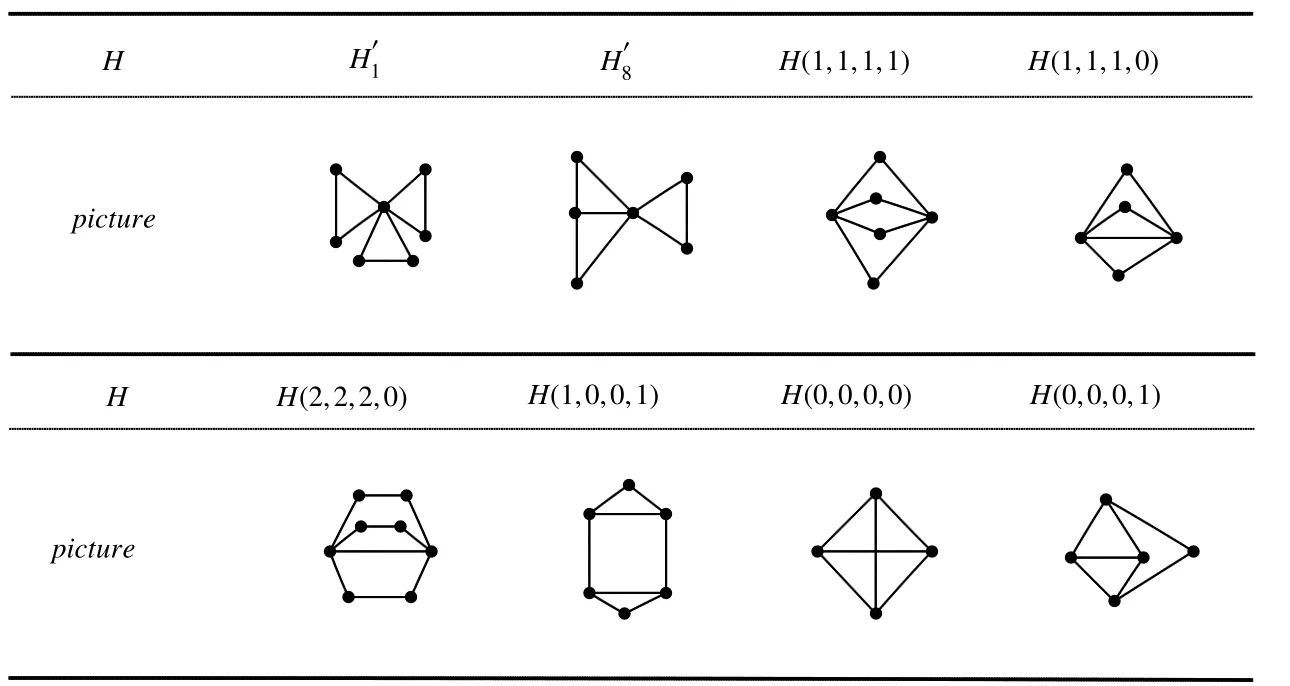
Table 6 All Laplacian integrals of tricyclic base-graph with c(H)≤6
We check on connected Laplacian integral tricyclic base-graph by computer,there is only one such graph founded withc(H)≥7 isH0(see in Figure 6),By direct computation we know thatS pecL(H0)=[0,13,22,43,5],which leads to the following problem.
Problem 1LetHbe a connected tricyclic base-graph withc(H)≥9,thenHis not Laplacian integral.
3 The Laplacian integral Tricyclic Graphs
For a general connected tricyclic graphs,it can be obtained from tricyclic base-graphs by joining some trees.In order to characterize the general connected Laplacian integral tricyclic graphs,we firstly give some important lemmas below.
Lemma 13[4]IfGis a connected graph of ordern(n≥2)with at least one pendant vertex,thenGis Laplacian integral if and only ifG=K1∨(K1∪H1),whereH1is Laplacian integral onn?2 vertices.
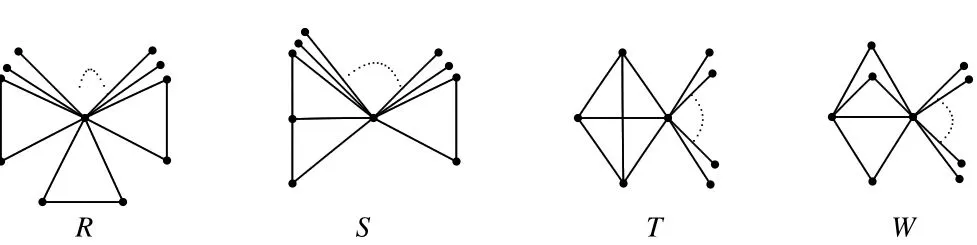
Fig 7 The graphs R,S,T and W
Theorem 2LetHbe a connected tricyclic graph of ordernwith at least one pendent,thenHis Laplacian integral if and only ifHR,S,T,Wwhere the corresponding graphs are shown in Figure 7.
ProofBy Lemma 13,we haveH=K1∨(K1∪H1).We see that the cycles ofHcomes from either the subgraphH1itself or the join ofH1andK1.Suppose thatH1haskedges.We claim thatk=3.In fact,ifk≥4 thenHmust contain at least four basic cycles,it is impossible;ifk≤2 thenHhas at most two basic cycles,it is also impossible.Thus,we divide the following cases.
Case 1H1={3P2}∪(n?8)K1;
Clearly,H1is Laplacian integral.HenceH=K1∨(K1∪H1)is Laplacian integral by Lemma 13.Thus we claim thatH=Rshown in Figure 7.
Case 2H1=P3∪P2∪(n?7)K1;
Clearly,H1is Laplacian integral.HenceH=K1∨(K1∪H1)is Laplacian integral by Lemma 13.In this case,we obtainH=Sshown in Figure 7.
Case 3H1=C3∪(n?5)K1;
Clearly,H1is Laplacian integral.HenceH=K1∨(K1∪H1)is Laplacian integral by Lemma 13.It follows thatH=Tshown in Figure 7.
Case 4H1=K1,3∪(n?6)K1;
Clearly,H1is Laplacian integral.HenceH=K1∨(K1∪H1)is Laplacian integral by Lemma 13.Thus we obtainH=Wshown in Figure 7.
Case 5H1=P4∪(n?6)K1;
SinceH1is not Laplacian integral.HenceH=K1∨(K1∪H1)is not Laplacian integral by Lemma 13.
It completes this proof.
Theorem 3LetHbe a connected Laplacian integral tricyclic graph of ordernwith at least one pendent,then it is determined by its Laplacian spectrum if it is Laplacian integral.
ProofLetMhas the same Laplacian spectrum asH,then λn?1(M)= λn?1(H)>0,which implies thatMis connected.Moreover,sinceMhas the same number of vertices,the number of edges asH,thusMis also a tricyclic graph.By Theorem 2,the connected Laplacian integral tricyclic graphs areR,S,TandW,and they have distinct Laplacian spectra,it follows thatMH.HenceHis determined by its Laplacian spectrum.
 新疆大學(xué)學(xué)報(自然科學(xué)版)(中英文)2014年1期
新疆大學(xué)學(xué)報(自然科學(xué)版)(中英文)2014年1期
- 新疆大學(xué)學(xué)報(自然科學(xué)版)(中英文)的其它文章
- Arc Connectivity of Balanced Half-transitive Digraphs?
- A Phosphoric Acid Pretreatment of Activated Carbon Supported Pd Catalyst for Acetylene Hydrochlorination?
- Keyword Language Identi fication in Uighur,Kazakh,Kyrgyz and Chinese Multi-lingual Dictionary System?
- 塔克拉瑪干沙漠腹地克里雅河尾閭圓沙三角洲沙質(zhì)沉積物粒度特征?
- 新疆加曼特金礦與阿希金礦的流體包裹體特征對比研究?
- Group von Neumann Algebra?
