Hydraulics of crest spillway with large unit discharge and low Froude number*
WU Jian-hua (吳建華), LICHENG Chun-zi (李程純子), MA Fei (馬飛), LI Tong-chun (李同春),WU Wei-wei (吳偉偉)
1. National Engineering Research Center of Water Resources Efficient Utilization and Engineering Safety,College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China,E-mail: jhwu@hhu.edu.cn 2. Hydraulic Structures design division, Hydrochina Huadong Engineering Corporation, Hangzhou 310014, China
Introduction
In the recent two decades, many hydropower projects have been constructed within China, except for several special high dams. The crest spillway of those projects is characterized by large unit discharge and low Froude number, and the slit-type energy dissipater placed at the outlet of the crest spillway is a proper selection for the efficient energy dissipation or the flow entering the river. Those schemes were used, such as in the Wuqiangxi Project in Hunan Province and Yantan project in Guanxi Zhuang Autonomous Region, with discharge of about 280 m2/s, in the Shannipo Project in Guizhou Province with 215 m2/s[1,2], in which the Froude number varies from 2.17 to 3.85.
The slit-type energy dissipater raises the frictionwithin the flow and the air entrainment to the flow through it due to the effects of the contraction of the energy dissipater and of the extensions of the flow in the vertical and longitudinal directions[3,4], so that the energy dissipation of the flow could be enhanced.
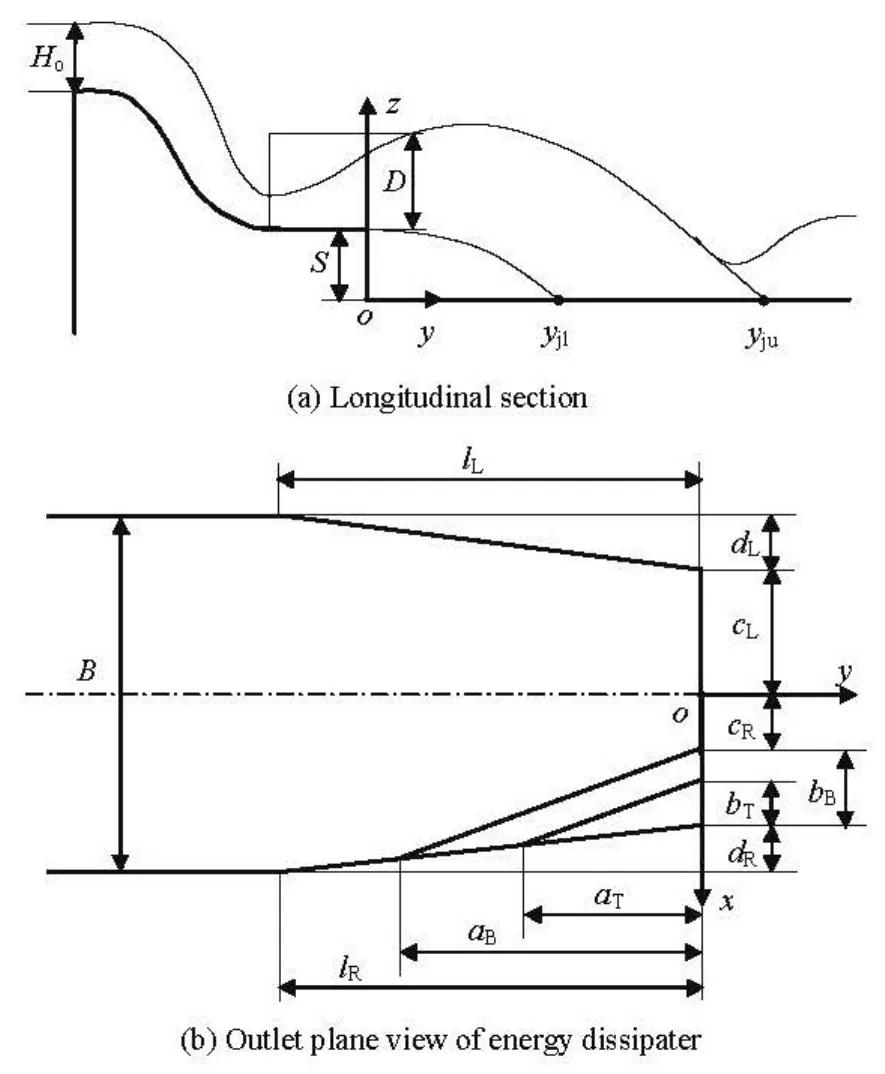
Fig.1 Definition sketch of experimental setup
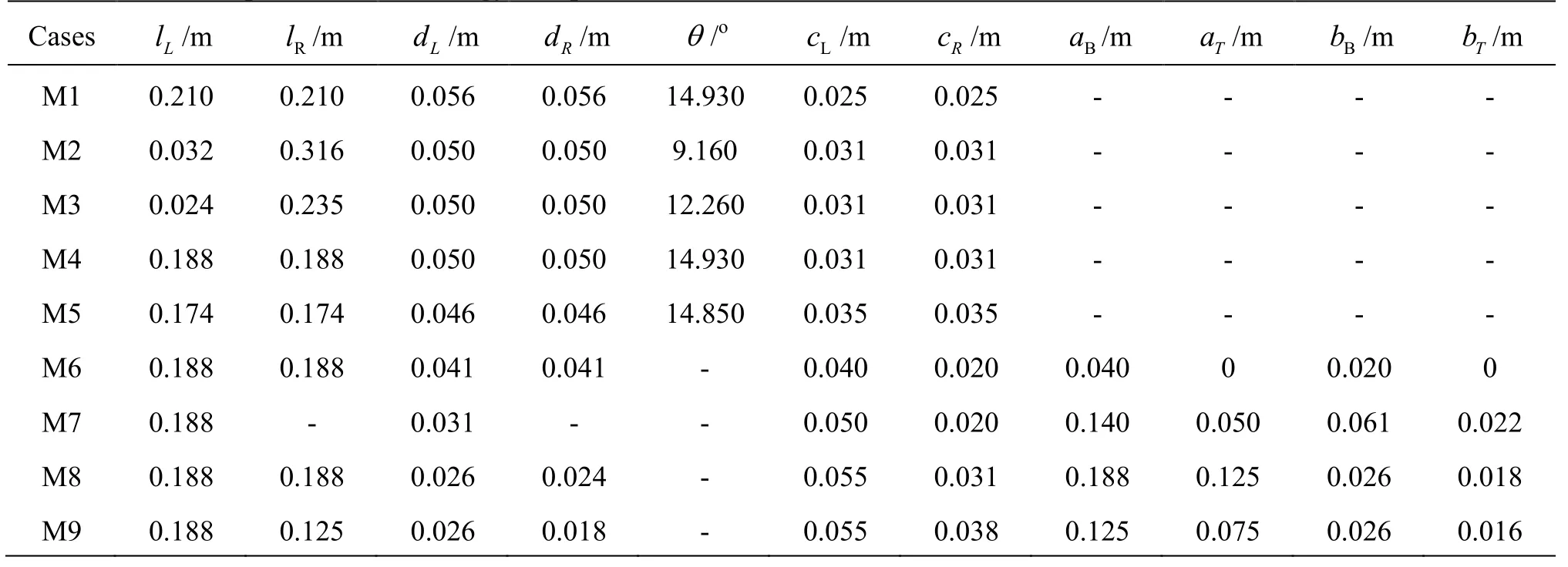
Table 1 Geometric parameters of energy dissipaters
For the slit-type energy dissipater at the outlet with free-surface flow, Liu and Qu[5]experimentally observed the section forms and the characteristics of the jet flow. Wu et al.[6]classified the flow as I-type and T-type and presented the conversion conditions of the flow types. Liu et al.[7]estimated the jet width for stilling basin designs. Ni and Liu[8]analyzed the abrupt deflected supercritical water flow. Furthermore, Wu et al.[9]developed the multiple slit-type energy dissipaters and their energy dissipation could be raised by 5%. Besides, Hager[10], Juon and Hager[11]and Lucas et al.[12]detailedly investigated the hydraulic characteristics of the various deflectors at the outlet by the physical model experiments. Those are all based on the orifice flow as the object, and they are of the characteristics that the flow Froude number increases when the water head increases. For the slit-type energy dissipater in the crest spillway, however, the flow through this energy dissipater has different behavior,i.e., the flow Froude number decreases and the flow choking appears easily when the water head increases.Meanwhile, the jet flow will impact to the river banks for narrow rivers. Therefore, it is crucial to investigate the hydraulics of this kind of the energy dissipater.
With the crest spillway of a certain hydropower project as the object, its height of the dam is 121.00 m.The crest spillway is divided into three parts with the width of 13.00 m and the slit-type energy dissipater is placed at the outlet of each part. The designed discharge is 11 080.00 m3/s and the unit discharge is about 284.00 m2/s at the design water level, and then the flow Froude number for the energy dissipaters varies from 1.2 to 2.2 under the conditions of operations.The objective of this paper is to investigate the hydraulics of the flow through the slit-type energy dissipater with the tetrahedron placed in the side wall of the outlet, including flow choking, flow impact to river banks, and jet trajectory.
1. Experimental setup and methodology
1.1 Experimental setup
The experiments were conducted in the High-Speed Flow Laboratory, Hohai University (Nanjing,China). The experimental setup consisted of a pump,an approach conduit, a large feeding basin, a test model, and a flow return system with discharge measurement weir instrument. The test model was designed at the scale of 1/80 on the basis of the Froude number criteria, including an upstream reservoir, a crest spillway, and a downstream river.
Figure 1 is the definition sketch of the experimental setup. The origin of the coordinate system (xyz)is at the riverbed downstream through the outlet plane center of the energy dissipater, and the axisxis back to the paper face. In this figure,S=0.750m is the height between the outlet bottom and the base level of the riverbed,Hois the water head of the crest of the spillway,yjlandyjuare the positions of the impact points of both the lower and upper jet trajectories onto the base level, respectively, determined visually from the river side, by extending the jet trajectory, andD=0.400 m is the wall height of the outlet energy dissipater (Fig.1(a)).
1.2 Experimental methodology
Table 1 is the geometric parameters of the energy dissipaters with nine cases, in which cases M1-M5 are the slit-type energy dissipaters, while cases M6-M9 are those with tetrahedron. In the table (see Fig.1(b)),B=0.163m is the width before the energy dissipater,lLandlRare the lengths of contraction section,anddLanddRare the contraction widths, respectively,aBandbBare the bottom lengths of the tetrahedron, whileaTandbTare their top lengths, respectively,cLandcRare the left and right widths of the outlet based on the center line, andC=cL+cR,θ=arctan(dL/lL), is the contraction angle for Cases M1-M5.

Fig.2 Phenomena and developing processes of flow choking(M4)
Cases M1-M5 serve as the variations of the flow characteristics with bothlL(orθ) andC, while Cases M6-M9 are designed for examining the effects of the various geometric parameters of the tetrahedrons.
2. Results and discussions
2.1 Flow choking
Figure 2 shows the phenomena and developing processes of the flow choking through the energy dissipater (Case M4). The roller occurs on the flow surface when the flow Froude number decreases to some critical value, due to the contraction effects of the slittype energy dissipater, which is called as flow choking.In Fig.2, the beginning position of the roller is stood denoted by Point A. The flow Froude number is given byFrB=VB/(ghB)0.5, where the subscript B expresses the lowest position of the crest spillway (see Fig.2(a)), and thenVBandhBare the average velocity and the depth of the flow at Point B, andg=9.81m/s2is the gravitational acceleration. It should be noticed that the flow Froude number decreases with increasing water head of the crest of the spillway,and then the flow choking appears and develops(Figs.2(a)-2(e)). Here, the critical flow choking is determined if the beginning point A gets to the section at point B, and we letdenotes the flow Froude number under the condition of critical flow choking (see Fig.2(d)).
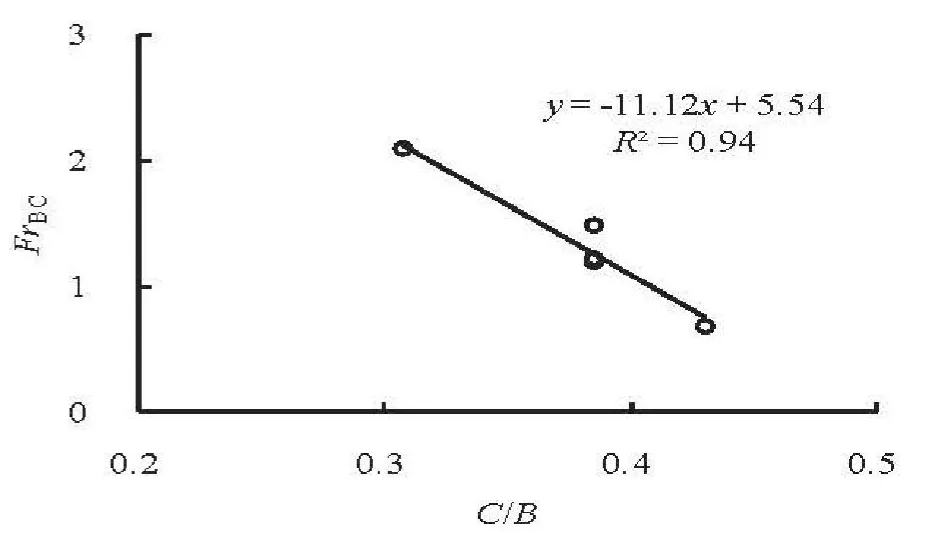
Fig.3 Variation of FrBC with C/B
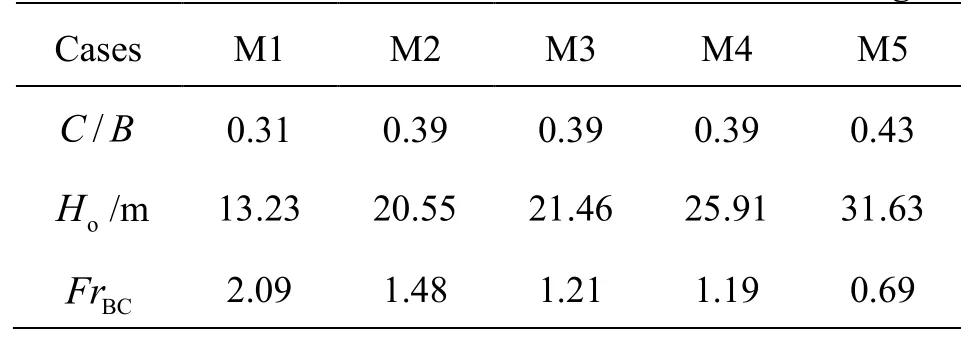
Table 2 Parameters and Froude number of flow choking
Given the definition of the critical Froude number mentioned above, Fig.3 and Table 2 present the variation ofFrBCwithC/Bfor cases M1-M5. The best fit is

The coefficient of determination isR2=0.94. Equation (1) demonstrates thatFrBC(C/B) descends linearly, which means that the increase of widthC/Bcould effectively modify the flow choking. However,since widthC/Bis closely related to the energy dissipation, it is necessary to comprehensively balance the effects of them when widthC/Bis determined.Secondly, it should be noticed that, the contraction angleθhas slight effect onFrBCfor cases M2-M4 although it varies from 9.16oto 14.93o, that is to say,FrBCis dominated byC/B.

Fig.4 Flow impact to river bank (M5, Ho=0.309m )
2.2 Flow impact to river bank
Figure 4 shows the flow regime of the side outlet of the crest spillway whenHo=0.309m for Case M5.With respect to a slit-type energy dissipater, the shock wave is brought about due to the contraction effect of the side walls. It could be seen from this figure that the jet flow impacts the river bank, with Point D denoting the position of the flow impact to the river bank.
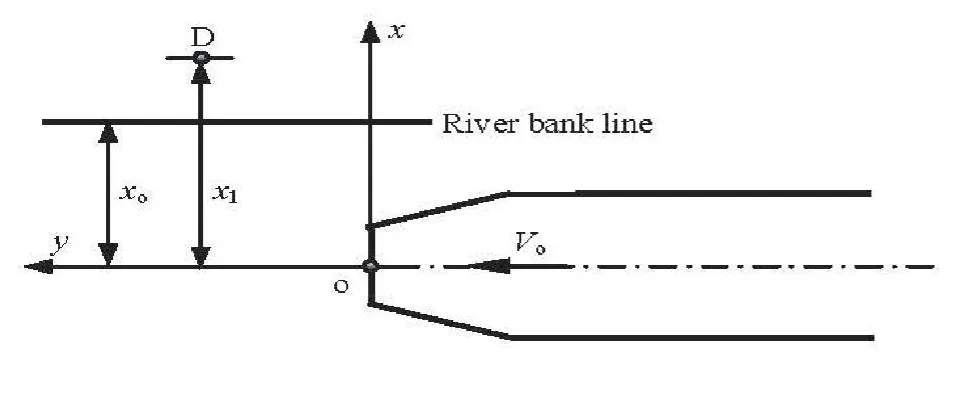
Fig.5 Definition sketch of flow impact to river bank
Figure 5 is the definition sketch of the flow impact to river bank, in whichxo=0.103m is the distance of the coordinate axisyto the river bank line,andx1is the distance of the axisyto Point D. We letX=x1-xo, standing for the range of the flow impact to the river bank. In this figure,Vois the average velocity of the flow.
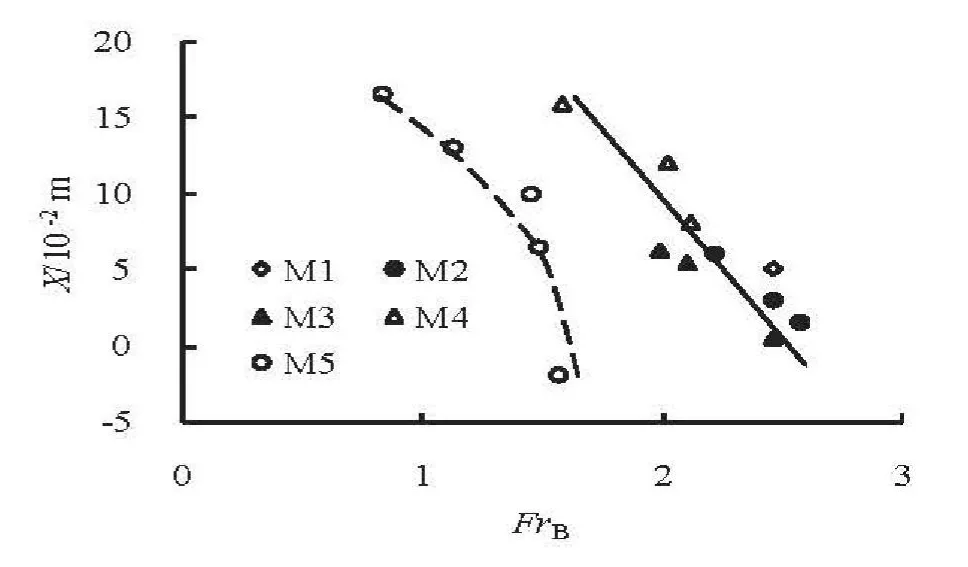
Fig.6 Variations of X with FrB for cases M1-M5
Figure 6 shows the variations ofXwithFrBfor the flow through the silt-type energy dissipater(Cases M1-M5 listed in Table 1), where the flow regimes are limited in the states of non-choking in order to compare the effects of the various cases onX. It could be noticed that the range of the flow impact to the river bank decreases as the flow Froude number increases. Secondly,X(FrB) is roughly at a line for Cases M1-M4, which meansθhas slight effect onX(FrB) at the ranges ofθ=9.16o-14.93oandC=0.050m-0.063m. Lastly,FrBfor Case M5 is less than those of cases M1-M4 because of the large width of the outlet (C=0.070m).
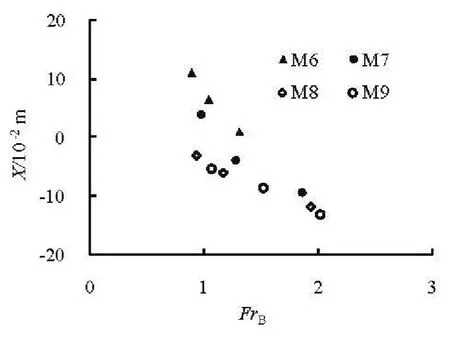
Fig.7 Variations of X with FrB for Cases M6-M9
It is well known that, for a slit-type energy dissipater, it is the shock wave that is a key factor resulting in the flow impact to river bank due to the sudden change of the side wall forms[13]. Theoretically, the flow direction could be deflected and this kind of shock wave should be balanced if a tetrahedron placed inside the side wall of the outlet in the river bank side. Secondly, through placing the tetrahedron, the form of the outlet is changed from rectangle to trapezoid, andthus there is still an extension effects on the flow at small discharge thanks to the narrow width near the outlet bottom, while for the large discharge, the jet trajectory could be adjusted owing to the gravitational effect of the water resulted from wide upper to narrow lower outlet.

Table 3 X / FrB for various tetrahedron outlets
Figure 7 and Table 3 are the variations ofXwithFrBfor the flow through the outlet with a tetrahedron (Cases M6-M9). From the geometric parameters listed in Table 1, it could be seen that the deflection effects of the tetrahedron depend directly on their parameters and forms. The flows, such as those in Cases M8 and M9, do not impact to the river bank(with the negative value ofX).
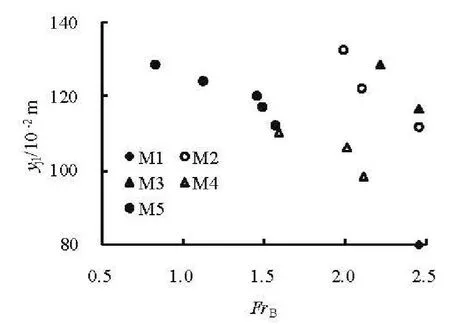
Fig.8 Variations of yjl with FrB for Cases M1-M5
2.3 Jet trajectory
The behavior of the jet flow, especially the extensions in the vertical and longitudinal directions and the jet trajectory through the slit-type energy dissipater, is directly related to the energy dissipation.Figures 8 and 9 are the distances of lower (yjl) and upper (yju) jet trajectories to the riverbed base level for the slit-type energy dissipaters (Cases M1-M5),and Figs.10 and 11 are those of lower (yjl) and upper(yju) jet trajectories for the tetrahedron outlets (Cases M6-M9), respectively. It could be noticed that, with respect to the slit-type energy dissipater, the distance increases for either lower or upper jet trajectory when the water head increases[14]or the flow Froude number decreases. While the tetrahedron outlets (Cases M6-M9) have the different properties of the jet trajectory,i.e., the jet distance decreases if the water head increases (see Figs.10 and 11). This result comes mainly from the gravitational effect of the wide upper on the narrow lower flow induced by the outlet form of those energy dissipaters.
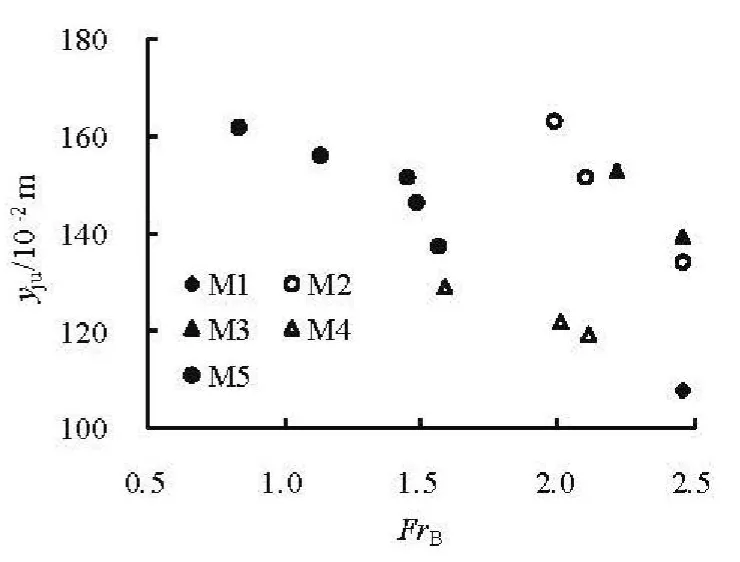
Fig.9 Variations of yju with FrB for Cases M1-M5
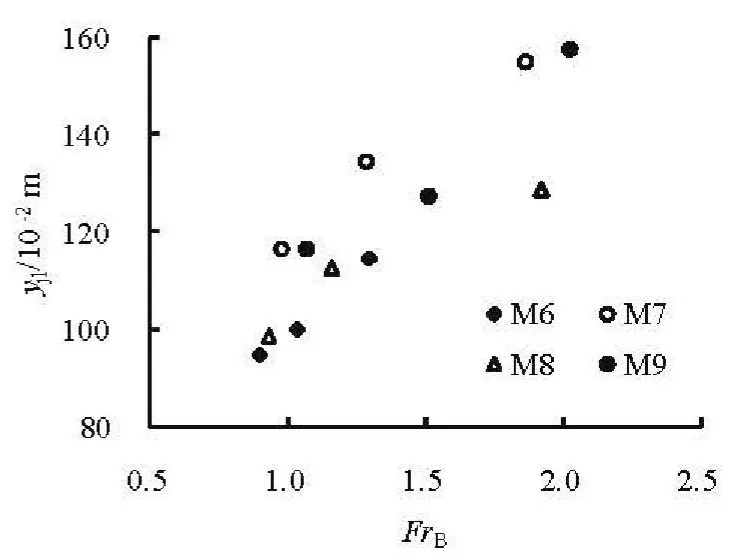
Fig.10 Variations of yjl with FrB for Cases M6-M9
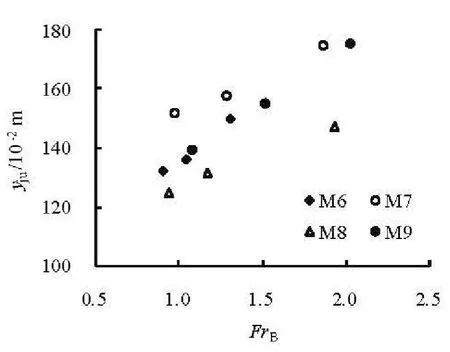
Fig.11 Variations of yju with FrB for Cases M6 -M9
3. Conclusion
For the crest spillway with large unit discharge and low Froude number, the slit-type energy dissipaters have been used in the outlet in order to increase energy dissipation. The flow choking occurs easily at lower Froude number. The critical Froude numberFrBC(C/B) is roughly linear if the flow Froude num-ber is expressed by the parameters at Point B before the slit-type energy dissipater. The impacts of the flow could be modified to the river bank when the tetrahedron is placed inside the side wall of the outlet at the river bank side because of the effect of its deflection on the flow. Compared the jet trajectory of the slittype energy dissipater, the distance decreases when the water head increases or the flow Froude number decreases, which is caused by the gravitational effect of wide upper on narrow lower water for the tetrahedron outlets.
[1] NI Han-gen, WANG Qing-guo and LIU Yu-chong et al.The application of unusual flaring piers to enhance energy dissipation of overflow discharge[J]. Journal of Hydraulic Engineering, 2000, 31(8): 55-59(in Chinese).
[2] XIAO Xing-bin. Summary of application of slot dissipator for high dam energy dissipation and its development[J]. Hydropower Station Designs, 2004, 20(3):76-81(in Chinese).
[3] WANG Hai-yun, DAI Guang-qing and YANG Qing et al. Flood discharge and energy dissipation with low water head and large unit discharge[J]. Water Power,2006, (8): 22-25(in Chinese).
[4] HUANG Qiu-jun, WU Jian-hua. Researvh on contraction energy dissipaters[J]. Journal of Hohai University (Natural Sciences), 2008, 36(2): 219-223(in Chinese).
[5] LIU Shi-he, QU Bo. Changes of section form for skijump flow[J]. Engineering Journal of Wuhan University, 2004, 37(5): 1-4(in Chinese).
[6] WU Jian-hua, MA Fei and YAO Li. Hydraulic characteristics of slit-type energy dissipaters[J]. Journal of Hydrodynamics, 2012, 24(6): 883-887.
[7] LIU Yang, MA Fei and WU Jian-hua. Shock wave and jet width slit-type flip bucket[J]. Advances in Science and Technology of Water Resources, 2014, 34(3): 20-24.
[8] NI Han-gen, LIU Ya-kun. Abrupt deflected supercritical water flow–revised theory of shock wave[J]. Journal of Hydrodynamics, 2006, 18(1): 32-39.
[9] WU Jian-hua, YAO Li and MA Fei. Hydraulics of a multiple slit-type energy dissipater[J]. Journal of Hydrodynamics, 2014, 26(1): 86-93.
[10] HAGER W. H. Deflector-generated jets[J]. Journal of Hydraulic Engineering, ASCE, 2010, 47(4): 466-475.
[11] JUON R., HAGER W. H. Flip bucket without and with deflectors[J]. Journal of Hydraulic Research, 2000,126(11): 837-845.
[12] LUCAS J., HAGER W. H. and BOES R. M. Deflector effect on chute flow[J]. Journal of Hydraulic Engineering, ASCE, 2013, 139(4): 444-449.
[13] NING Li-zhong, DAI Zheng-seng. Calculations of shock wave and controlling water depth in region of contraction on slit-type flip bucket[J]. Journal of Xi’an University of Technology, 1992, 8(3): 197-240, 215(in Chinese).
[14] SUN Jian, LI Yu-zhu. Optimization of space between flows into stilling basin for high arch dam[J]. Water Resources and Hydropower Engineering, 2003, 34(1):52-54(in Chinese).
 水動(dòng)力學(xué)研究與進(jìn)展 B輯2015年2期
水動(dòng)力學(xué)研究與進(jìn)展 B輯2015年2期
- 水動(dòng)力學(xué)研究與進(jìn)展 B輯的其它文章
- A general framework for verification and validation of large eddy simulations*
- Direct calculation method of roll damping based on three-dimensional CFD approach*
- Visualization study on fluid distribution and end effects in core flow experiments with low-field mri method*
- Large-eddy simulation of the flow past both finite and infinite circular cylinders at Re =3900*
- Safe operation of inverted siphon during ice period*
- Flow field simulation of supercritical carbon dioxide jet: Comparison and sensitivity analysis*
