Hui Huang and Hidekazu Murakawa

1 Introduction

Owing to the development of computer technology,numerical simulation of welding deformation and residual stress is now receiving increasing attention from academic and engineering fields.The thermo-mechanical finite element analysis can well reproduce the stress and strain field under complex conditions,such as bead shape,welding sequence and component interaction.However,the strong nonlinearity and transient feature associated with the welding process prohibit the application of presently available tools to large industrial scale problems.In the past two decades,extensive efforts to improve the computation performance have been paid on different techniques such as modeling scheme and solution algorithm.

Sarkani(2000),Deng(2006)and Barsoum(2009)studied the formation of the welding residual stresses by 2D and 3D simulations separately,and they found that 2D prediction shows good agreement with measurements,hence computational time can be greatly reduced compared with 3D simulations.N?sstr?m(1992)modeled a welding component using solid elements in and near the weld but shell elements elsewhere.The combination of solid elements and shell elements could reduce the number of degree of freedom(DOF)in the welding problem.

Karlsson(2011)and Bhatti(2012)employed the block-dumping approach in thermomechanical analysis for prediction of welding deformation and residual stresses.The approach can reduce the number of time steps significantly and keep satisfactory accuracy in welding simulation.Ding(2014)employed the concept of peak temperature to determine the residual stress and deformation during wire and arc additive manufacturing.

Biswas and Mandal(2008)developed an analysis methodology based on the quasistationary nature of welding and symmetry of model for studying the distortion pattern of orthogonally stiffened large plate panels.Moreover,a comparison was made for prediction of welding distortions in a stiffened plate panel among three different FE approaches,namely the transient thermomechanical analysis and two different equivalent techniques,inherent strain method and transient cooling phase analysis by Biswas and Mandal(2009).

In aspect of solution algorithm,Murakawa(2005)proposed the iterative substructure method which maintains high accuracy for various cases.The basic idea is to solve the weakly nonlinear region A and strongly nonlinear region B interactively,and complete the iteration until the residual force on the interface between region A and region B vanishes.Nishikawa(2007)presented several actual applications of ISM,the high accuracy and efficiency had been well validated.It has also been pointed out that the ISM is most efficient for models with DOF less than 1 million,because the computation time of region A is primary for large scale problem(Murakawa,2015).Bhatti(2014)employed the substructure approach in analysis of a large complex welded structure,and they obtained welding residual stresses with acceptable accuracy in much shorter time than direct solution with full structure.Ikushima and Shibahara(2014)applied the explicit scheme in solving welding thermal mechanical problem with a GPU acceleration technique.

In the framework of adaptive methods,Brown and Song(1993)presented the remeshing method and substructure method using a shell model.Heating along the edge of a plate was analyzed,and a reduction of computation time of analysis without remeshing to one seventh was realized with qualitative accuracy in results.Lendgren(1997)developed the 3D remeshing technique by means of a node-number variable element to fit the mesh transition zone.An improvement of computation efficiency by about 4 times was achieved.Duranton(2004)proposed an adaptive meshing technique with constraint elements to decrease the computation costs while keeping good accuracy of the results.Regarding these remeshing methods,mesh coarsening effect on residual stress and plastic strain was not discussed,although interpolation and mapping procedures generally induce nonnegligible error in solution variables in strongly nonlinear problems.

Huang and Murakawa(2013)developed the dynamic mesh refining method(DMRM)based on the characteristic of welding problems.A background mesh was originally proposed to save and update the values of stress and strain.Enhancement on computation efficiency by 6 times had been realized with good accuracy by using onelevel refinement.

Recently,the DMRM was extended to refinement in multi-level hierarchical mode,so the number of DOFs could be further decreased.Moreover,the DMRM was incorporated with the ISM to establish a powerful tool for thermo-mechanical analysis.Two examples of fillet welding were shown in the present study,and a comparison between the in-house code JWRIAN*using multi-level DMRM-ISM,and a general purpose code ABAQUS had been made to validate the accuracy and efficiency of proposed method.

2 Dynamic mesh refining method with multi-level refinement

2.1 Basic concept

In welding problems,intensive heat is concentrated in the vicinity of the moving heat source.Therefore strong nonlinearity arises with high temperature in region B while the remaining region,region A+R,stays in a weakly nonlinear state with lower temperature(Fig.1).It becomes natural that a fine mesh needs to be used in region B and the region nearby namely region R and a coarse mesh can be used elsewhere.For this purpose,refinement on an initial mesh(IM)with coarse elements can be adopted.The fine mesh is then moved with the heat source,and the elements in the welded zone behind the heat source return back to coarse mesh.In this case,large number of DOFs can be reduced when displacement field is solved on this computational mesh(CM),see Fig.1.Different from conventional remeshing methods,a background mesh(BM)with fine elements near the weld is designed to save and update the solution of the global model.It can be updated with a larger time step since the fine mesh zone is always solved and updated by the CM.Meanwhile,coarse mesh zone has much weaker nonlinearity compared with fine mesh zone.

2.2 Hierarchical modeling

The initial mesh is refined hierarchically based on the region of refinement and size of the element.As shown in Fig.2,an orientation-based refinement was designed,so that the element was allowed to be subdivided into single or multiple directions.In the present study,the divisions were limited as 1≤m,n,p≤2 for simplicity of programming.Figure 3 shows the refining process of a fillet joint model by twolevel refinement.At the 2ndlevel refinement,the elements located at the weld was subdivided in the welding direction only.

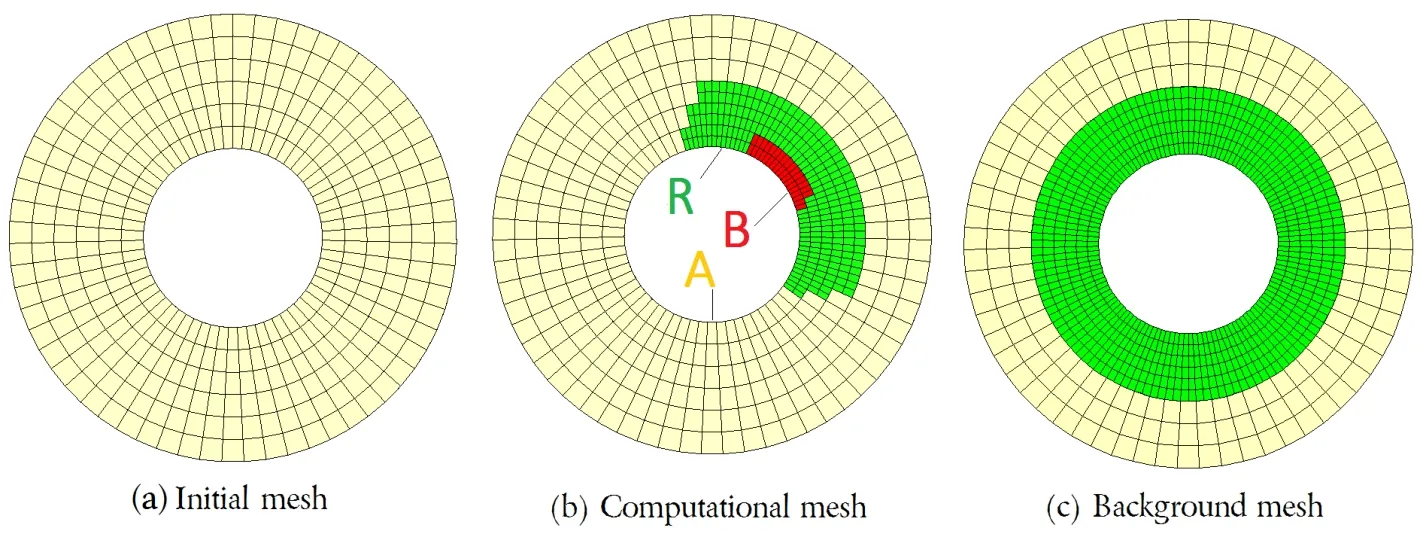
Figure 1:Various meshes employed in dynamic mesh refining method.

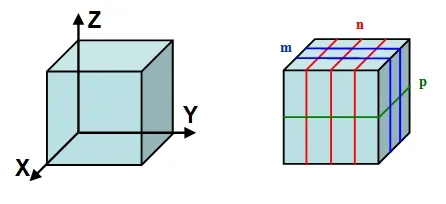
Figure 2:Refinement schemes for a hexahedral element.

Figure 3:Mesh Refinement of a fillet joint model:(a)Initial mesh(b)1stlevel refining(c)2ndlevel refining.

The interface between a parent elementEp(levellelement)and an adjacent child elementEc(levell+1 element)is connected through linear constraint relationship.The interfacial nodes which are shared only by elements on single side are termed as dummy nodes,and those shared by elements on both sides are termed as real nodes.A straightforward discretization of the constraint with respect to element stiffness and load vector was realized.The equivalent stiffness matrix and load vector of elementEcis calculated from its transformation matrixT,which describes the relation between dummy nodes and real nodes.

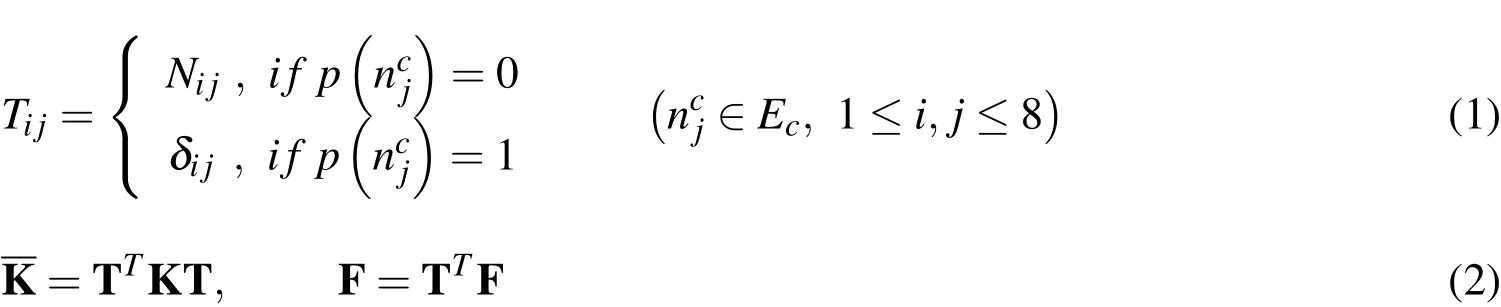
3 Combination of DMRM with ISM

3.1 Features of two numerical methods

In general computation methods,including the DMRM,all regions are solved as a whole simultaneously.The iterations until convergence basically depends on the strongly nonlinear region B,which takes up just a small portion of the whole model.Therefore,large amount of computation cost are spent to solve region A every step and every iteration together with region B.To solve the two regions separately,the iterative substructure method has been developed.However,the mesh predefined with fine elements near the weld does not change during the whole analysis.Therefore it should contain the whole weld line and its vicinity,even with region B ia only a part of this fine mesh around the moving heat source.

In the case of the dynamic mesh refining method the fine mesh is adaptively created around the transient position of the heat source.The number of DOFs to be solved can be greatly reduced compared with a fixed mesh containing the whole weld line.Therefore,it can be seen that,the dynamic mesh refining method reduces the unknowns in the global region A by having coarse elements at and around the weld line away from the heat source;and the iterative substructure method deals with nonlinearity in the local region B without having to solve region A in each step and each iteration with region B.Combine the two different techniques has large potential in solving large scale thermo-mechanical problems.

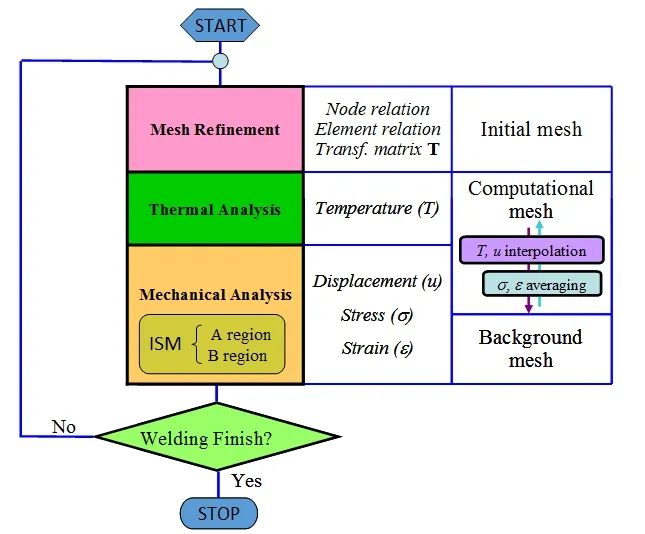
Figure 4:Computation flow of JWRIAN*.

3.2 Computation flowchart

Due to the complexity of original ISM program,a modified ISM[Huang(2015)]which solves region B only at the beginning of each time step was implemented in the current code JWRIAN*.Another advantage to use mod-ISM is that,large deformation problems can also be well solved because the direct coupling between region A and region B is removed.

The detailed computation flowchart of JWRIAN*is shown in Fig.4.Three main modules including mesh refinement,thermal analysis and mechanical analysis are organized in a loop.The iterative substructure method is only employed in the mechanical analysis which generally takes up most part of the computation time.The relation among initial mesh,computational mesh and background mesh is depicted in the flowchart.

4 Examples and Discussions

4.1 Fillet welding of a flange to a pipe

A flange-to-pipe welding problem as shown in Fig.5 was analyzed by the inhouse codes JWRIAN(ISM),JWRIAN*(DMRM-ISM)and a general purpose code ABAQUS 6.10?.Automatic time increment control was adopted in ABAQUS to achieve the maximum speedup.Double ellipsoidal heat source was used to model the heat flux generated by welding torch.The weld metal and base metal were defined as the same material SM400A.Temperature at four points on the section 90 degree from the welding start position as evaluated by JWRIAN*and ABAQUS were compared to each other.As shown in Fig.6,the temperature profiles calculated by the two codes have good correlation except for small deviations at peak values.The differences in numerical aspects such as transient heating region and integration scheme of thermal equation could be reasons for these deviations.

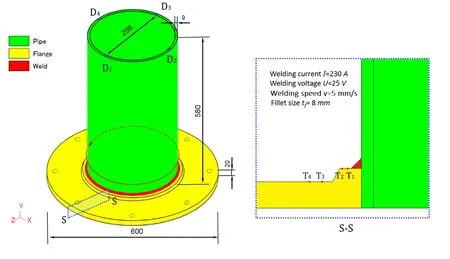
Figure 5:Geometrical model of flange welding.

Figure 7 shows a comparison of transient axial displacements at another four points on the top of the pipe.The four points were displaced in the Y negative direction due to the angular distortion between the pipe and the flange.After the welded component completely cooled down,the contour of hoop stress on section S-S of Fig.5 is plotted in Fig.8.It can be confirmed that,the solution obtained by JWRIAN*has almost the same accuracy as that by ABAQUS.

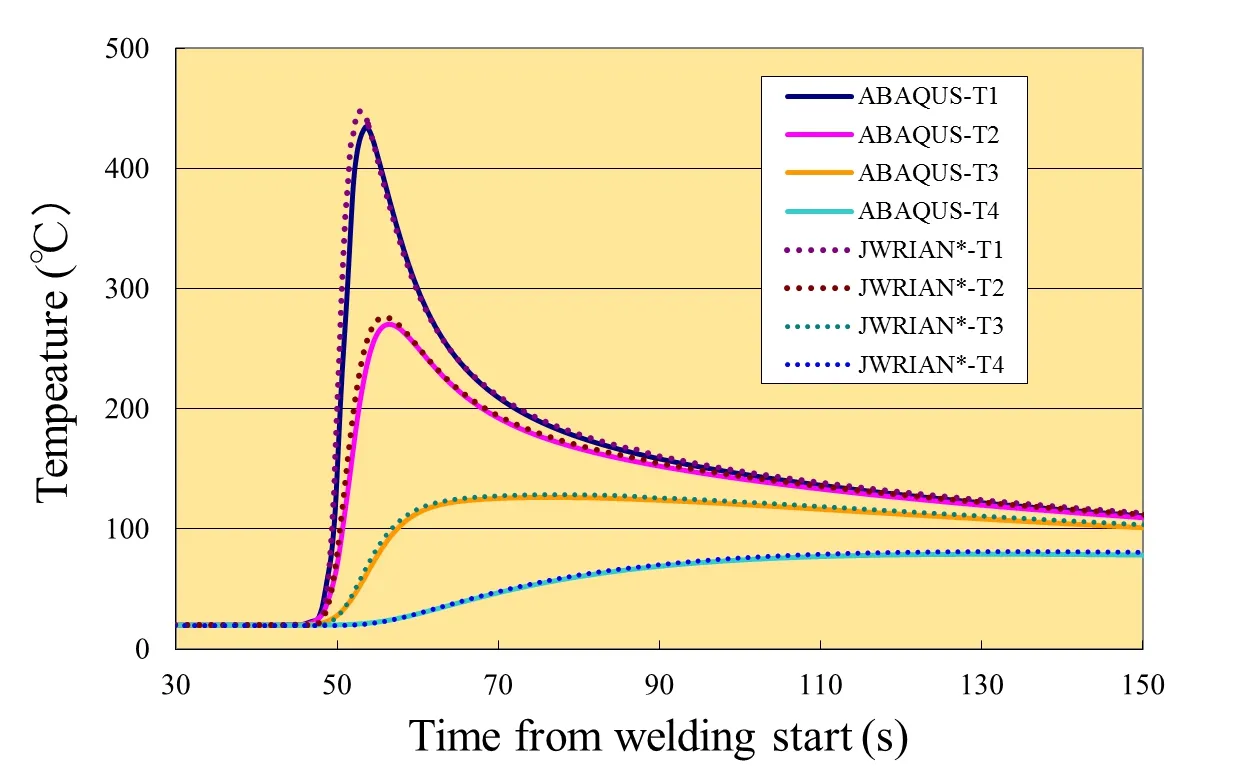
Figure 6:Transient temperature at evaluating points T1-T4.

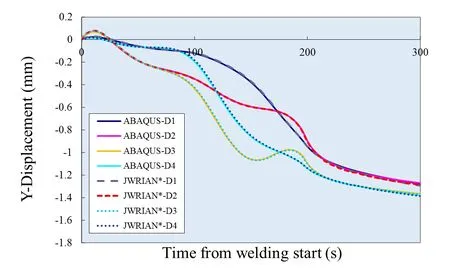
Figure 7:Transient displacements at evaluation points D1-D4.

In JWRIAN*,the number of elements included in B region and those in the computational mesh during each time step is summarized in Fig.9.At the start of welding,the number of elements in both regions increased;while at the intermediate welding stage,the elements did not change appreciably due to the quasi-steady state of temperature field.The averaged ratiosEB/EBMandECM/EBMare 1.7%and 27.9%respectively.Where,EB,ECMis the averaged number of elements during all time steps in B region and computational mesh,respectively.EBMis the number of elements in the background mesh.As indicated by Table 1,the analysis using JWRIAN took much less time than ABAQUS,and the time ratio was about 1/18.By introducing DMRM in JWRIAN*,the computation time was further reduced to 1/56.

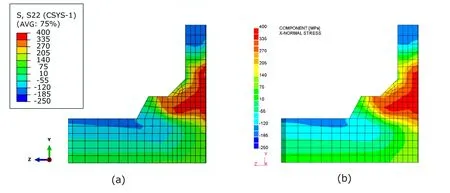
Figure 8:Contours of residual hoop stress:(a)by ABAQUS(b)by JWRIAN*.

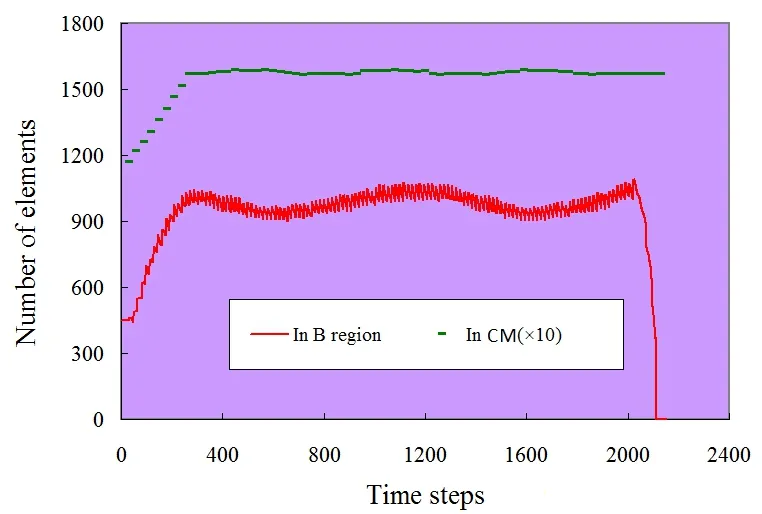
Figure 9:Evolution of elements in B region and computational mesh.

Table 1:Computation time for each code(unit:hour).

4.2 Welding of a stiffened panel

Welding of the stiffened panel shown in Fig.10[Deng(2008)]was analyzed by the proposed DMRM-ISM method.Before welding,there was no initial gap between the stiffeners and plate in Model-A,while a gap with a maximum value of 10mm existed in Model-B.Initial imperfection has been introduced and the gap was closed then welding was carried out.The mitigation process was supposed to be thermo-elastic in the numerical model,and an artificial temperature gradient was introduced in the stiffeners.For each model,the background mesh contained 1,391,709 unknowns,and the total number of time steps was 9,565.

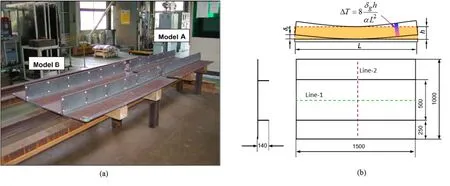
Figure 10:Two-stiffener welded structure:(a)Experimental model(b)Dimension and gap mitigation.

The longitudinal stresses on middle transverse section are shown in Fig.11.Apparently,the final pass dominated the stress distribution by the annealing effect it has on the previous pass nearby.A bending stress field through plate thickness can be observed in Model-B,which seems to be the result of initial stress induced by closing the gap.The global residual stress distribution of Model-B is shown in Fig.12.

The contours of displacement are shown in Fig.13,and the deflection along two lines,line 1 and line 2 in Fig.10,is shown in Fig.14-15.It is obvious that,Model-B had a much large deflection than Model-A,which is the result of additional deformation by initial imperfection.However,the angular distortion of the two models had very little difference.The results of thermo-mechanical simulation agreed very well with experimental measurements as can be seen in Figs.14 and 15.

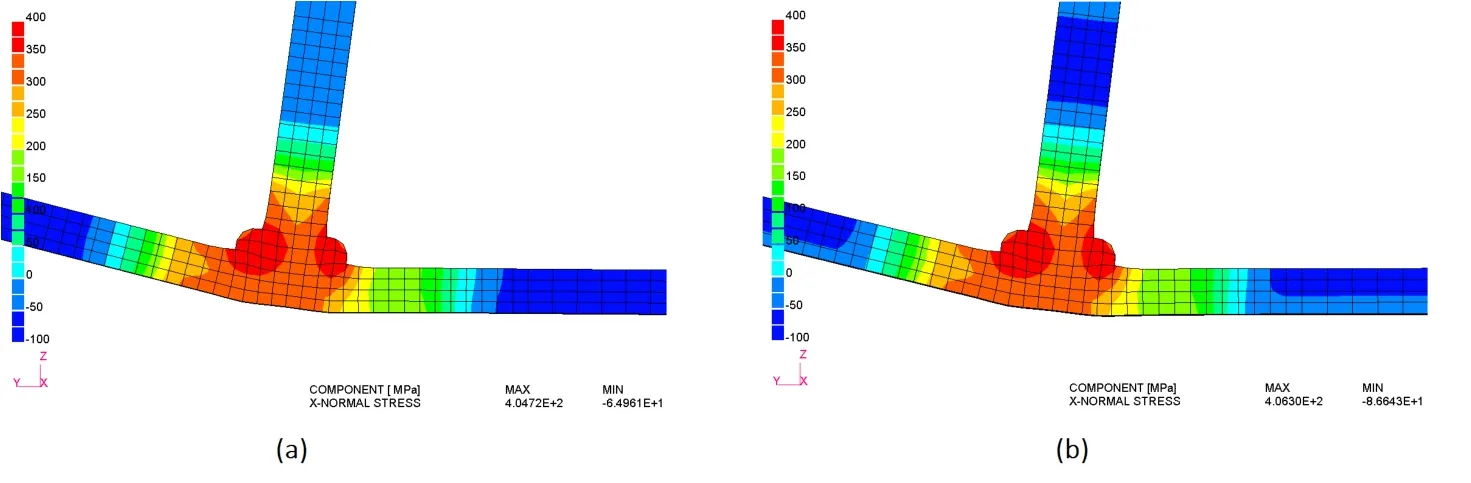
Figure 11:Longitudinal residual stresses on middle transverse section:(a)Model-A(b)Model-B.

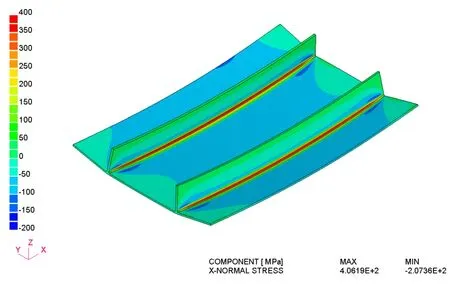
Figure 12:Global longitudinal stress of Model-B.

For the computation cost,a comparison between JWRIAN and JWRIAN*is shown in Table 2.It can be concluded that,the incorporation of refining method enhanced the computation speed of the ISM by 11.3 times,which can be roughly estimated by the ratioEBM/ECM=17.4.Saving in computation time can be even much more in larger scale models.

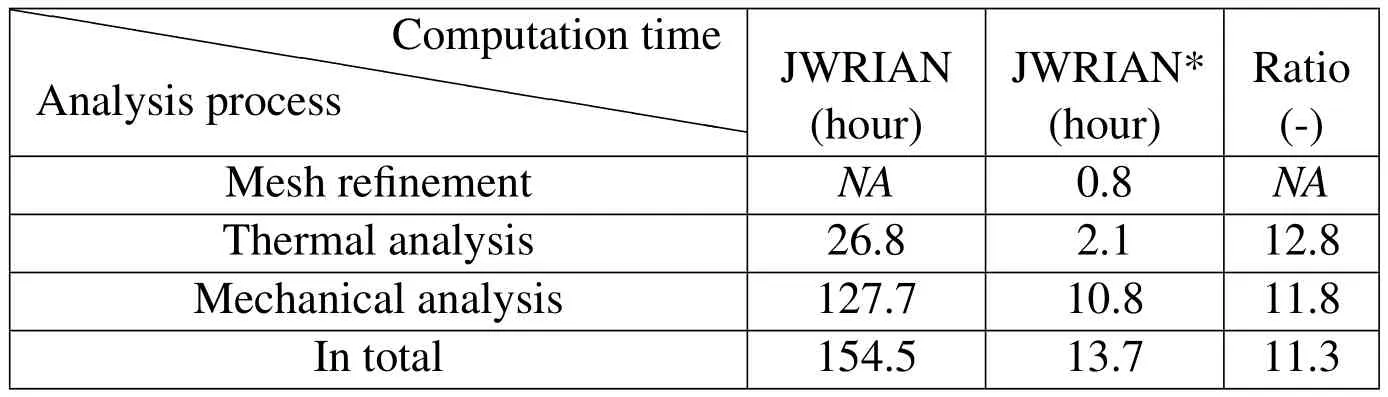
Table 2:Comparison between JWRIAN and JWRIAN*.

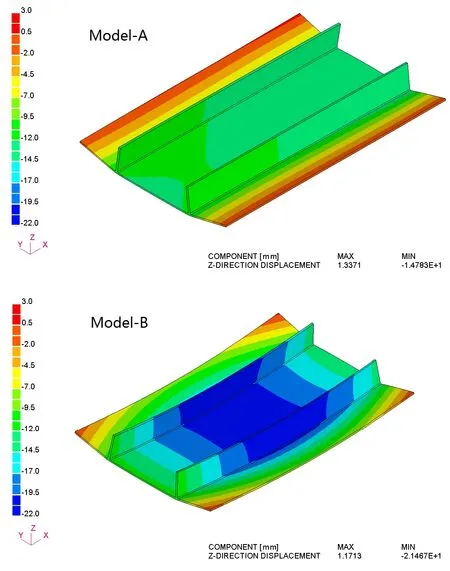
Figure 13:Comparison of out-of-plane deformation between two models:(a)Model-A(b)Model-B.

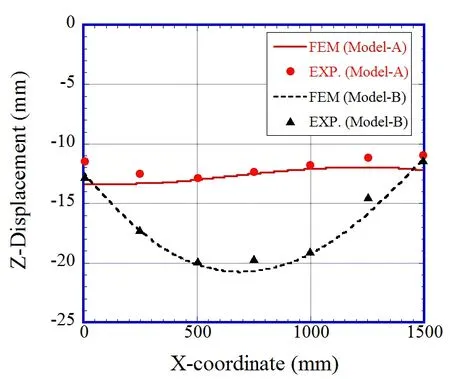
Figure 14:Deflection along Line-1 after welding.

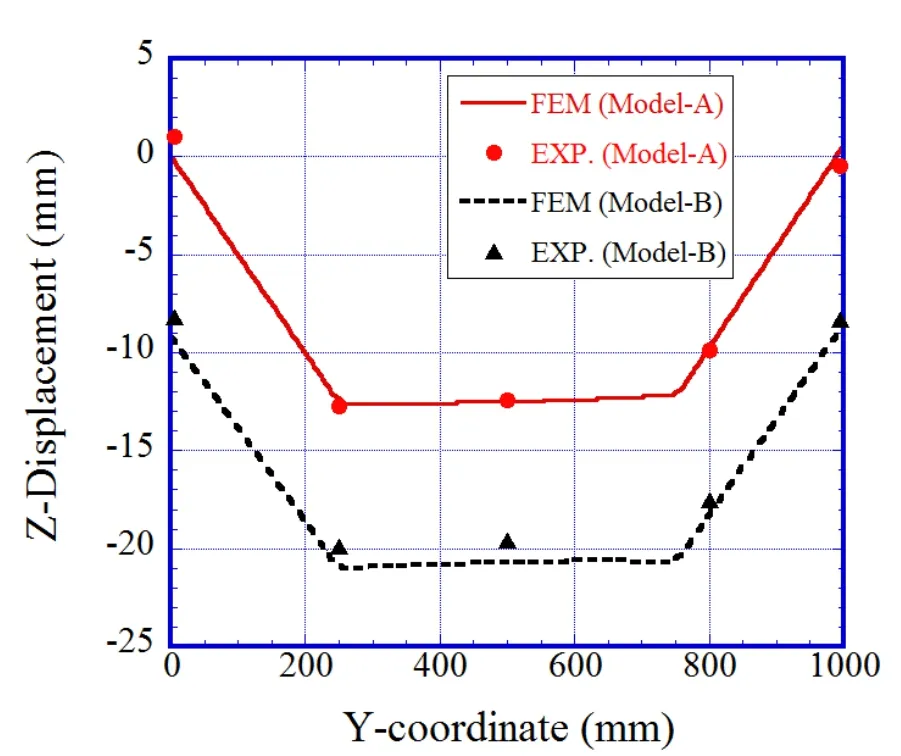
Figure 15:Deflection along Line-2 after welding.

5 Conclusions

The novel techniques-dynamic mesh refining method and iterative substructure method were successfully combined to solve large scale thermo-mechanical problems.The nature of welding problems was fully taken advantage of to reduce the computation cost.From the above study,the following conclusions were drawn:

(1)By analyzing a flange-to-pipe welding model with 207,090 unknowns,it was demonstrated that,the computation time of latest version of JWRIAN*consumes just 1/56 of the time that used by ABAQUS,while the solution accuracy of the two codes are comparable.

(2)Mesh refinement in single/multiple direction mode was realized in three-dimensional models.Multi-level refinement could bring large amount of reduction in degrees of freedom.

(3)A large scale fillet welded structure with over 1.3 million unknowns was analyzed by the proposed method,and the computation was completed within 14 hours.

(4)The implementation of DMRM speedups the analysis of ISM with a ratio close to the value ofEBM/ECM.

Barsoum,Z.;Lundb?ck,A.(2009):Simplified FE welding simulation of fillet welds–3D effects on the formation residual stresses.Eng.Fail.Anal.,vol.16,no.7,pp.2281-2289.

Bhatti,A.A.;Barsoum,Z.(2012):Development of efficient three-dimensional welding simulation approach for residual stress estimation in different welded joints.J.Strain.Anal.Eng.Des.,vol.47,no.8,pp.539-552.

Bhatti,A.A.,Barsoum,Z.,Khurshid,M.(2014):Development of a finite element simulation framework for the prediction of residual stresses in large welded structures.Comput.Struct.,vol.133,pp.1-11.

Biswas,P.;Mandal,N.R.(2008):Welding distortion simulation of large stiffened plate panels.J.Ship Prod.,vol.24,no.1,pp.50-56.

Biswas,P.;Mandal,N.R.(2009):A comparative study of three different approaches of FE analysis for prediction of welding distortion of orthogonally stiffened plate panels.J.Ship Prod.,vol.25,no.4,pp.191-197.

Brown,S.B.;Song,H.(1993):Rezoning and dynamic substructuring techniques in FEM simulations of welding processes.J.Manuf.Sci.Eng.,vol.115,no.4,pp.415-423.

Deng,D.;Murakawa,H.(2006):Numerical simulation of temperature field and residual stress in multi-pass welds in stainless steel pipe and comparison with experimental measurements.Comp.Mater.Sci.,vol.37,no.3,pp.269-277.

Deng,D.;Murakawa,H.;Liang,W.(2008):Prediction of welding distortion in a curved plate structure by means of elastic finite element method.J.Mater.Process.Technol.,vol.203,pp.1252-266.

Ding,J.;Colegrove,P.;Mehnen,J.;Williams,S.;Wang,F.;Almeida,P.S.(2014):A computationally efficient finite element model of wire and arc additive manufacture.Int.J.Adv.Manuf.Tech.,vol.70,no.1-4,pp.227-236.

Duranton,P.;Devaux,J.;Robin,V.;Gilles,P.;Bergheau,J.M.(2004):3D modelling of multipass welding of a 316L stainless steel pipe.J.Mater.Process.Technol.,vol.153,pp.457-463.

Huang,H.;Murakawa,H.(2013):Development of dynamic mesh refining method for large scale thermal and mechanical analysis in welding and line heating.Trans.JWRI,vol.42,no.1,pp.63-70.

Huang,H.;Ma,N.;Hashimoto,T.;Murakawa,H.(2015):Welding deformation and residual stresses in arc welded lap joints by modified iterative analysis.Sci.Technol.Weld.Join.,vol.20,no.7,pp.571-577.

Ikushima,K.;Shibahara,M.(2014):Prediction of residual stresses in multi-pass welded joint using Idealized Explicit FEM accelerated by a GPU.Comp.Mater.Sci.,vol.93,pp.62-67.

Karlsson,L.;Pahkamaa,A.;Karlberg,M.;L?fstrand,M.;Goldak,J.;Pavasson,J.(2011):Mechanics of materials and structures:a simulation-driven design approach.J.Mech.of Mater.Struct.,vol.6,no.1,pp.277-301.

Lindgren,L.E.;H?ggblad,H.A.;McDill,J.M.J.;Oddy,A.S.(1997):Automatic remeshing for three-dimensional finite element simulation of welding.Comput.Methods in Appl.Mech.Eng.,vol.147,no.3,pp.401-409.

Murakawa,H.;Oda,I.;Itoh,S.;Serizwa,H.;Shibahara,M.(2004):Iterative substructure method for fast FEM analysis of mechanical problems in welding.Preprints of the National Meeting of JWS.,vol.75,pp.274-275.

Murakawa,H.;Ma,N.;Huang,H.(2015):Iterative substructure method employing concept of inherent strain for large-scale welding problems.Weld World,vol.59,no.1,pp.53-63.

N?sstr?m,M.;Wikander,L.;Karlsson,L.;Lindgren,L.E.;Goldak,J.(1992):Combined solid and shell element modelling of welding.Mechanical Effects of Welding,Springer Berlin Heidelberg,pp.197-205.

Nishikawa,H.;Serizawa,H.;Murakawa,H.(2007):Actual application of FEM to analysis of large scale mechanical problems in welding.Sci.Technol.Weld.Join.,vol.12,no.2,pp.147-152.

Sarkani,S.;Tritchkov,V.;Michaelov,G.(2000):An efficient approach for computing residual stresses in welded joints.Finite Elem.Anal.Des.,vol.35,no.3,pp.247-268.