Hui YinDejie YuShengwen Yin and Baizhan Xia

A New Hybrid Uncertain Analysis Method and its Application to Acoustic Field with Random and Interval Parameters

Hui Yin1,Dejie Yu1,2,Shengwen Yin1and Baizhan Xia1

This paper presents a new hybrid Chebyshev-perturbation method(HCPM)forthe prediction ofacoustic field with random and intervalparameters.In HCPM,the perturbation method based on the first-order Taylor series that accounts for the random uncertainty is organically integrated with the first-order Chebyshev polynomials that deal with the interval uncertainty;specifically,a random interval function is firstly expanded with the first-order Taylor series by treating the interval variables as constants,and the expressions of the expectation and variance can be obtained by using the random moment method;then the expectation and variance of the function are approximated by using the first-order Chebyshev polynomials;the bounds of the expectation and variance are finally obtained by using the Monte Carlo method.Numerical results on two acoustic models verify that the accuracy of HCPM is better than that of the hybrid perturbation method(HPM).

Perturbation method,Chebyshev polynomials,acoustic field prediction,random variables,interval variables.

1 Introduction

In recentyears,numericalmethods forthe response analysisofengineering systems with deterministic parameters have received lots of attention and developed rapidly.However,uncertainties caused by environmental factors,manufacturing tolerances or unpredictable external excitations are unavoidable in engineering practice.Thus it is very important to perform the uncertain analysis in engineering systems,especially for the systems that are sensitive to the uncertain parameters.Generally all uncertain parameters can be described as two different models:the probabilisticand non-probabilistic models.If the information about the uncertain parameters is sufficient to define the probability distribution functions unambiguously,the probabilistic model can be the prior way to describe the uncertain parameters[Stefanou(2009);Kami′nski and Lauke(2013)];if the objective information about the uncertain parameters is limited and it is difficult to construct the probability distribution functions,the non-probabilistic model is suitable for describing uncertain parameters.Many probabilistic methods have been proposed for the response analysis of engineering systems with random parameters.The Monte Carlo method(MCM)is a widely used approach for stochastic problems due to its simplicity of implementation[Hurtado and Barbat(1998);Fishman(1996)].However,the computational cost of MCM is usually too high to be acceptable for large-scale engineering systems,and thus its applications are limited.The spectral stochastic method is an efficient approach based on polynomial chaos series for stochastic problems[Shang and Yun(2013);Chen and Soares(2008);Chung,Gutiérrez,Graham-Brady and Lingen(2005)],but the application of it is still limited to the stochastic problems with a few variables.Based on the Neumann expansion and the Taylor series expansion,the perturbation stochastic method was developed for stochastic problems[?avdar,Bayraktar,?avdar and Adanur(2008);Kaminski(2010);Liu,Belytschko and Mani(1986)].Due to the neglect of higher order terms of Taylor series,the application of the perturbation stochastic method is limited to the stochastic problems with small uncertain ranges of parameters.

Non-probabilistic model is an alternative that can be perfectly applied to represent the uncertain parameters with insufficient information for constructing the probability distribution functions,such as the convex model and the interval model[Qiu(2003);Hua and Qiu(2010);Jiang,Bi,Lu and Han(2013);Li,Luo,Rong and Hu(2013);Moore(1966)].For the convex model,the uncertain parameters are expressed as the convex-set variables whose variation bounds are defined,and the least and most favorable responses of the uncertain problems can be obtained by using an anti-optimization approach.For the interval model,the lower and upper bounds are well-defined,and the lower and upper bounds of the response of an uncertain problem can be obtained by employing the interval analysis methods.Many interval methods have been developed for the interval uncertain problems and have achieved significant progress.MCM can also be used to deal with the interval uncertain problems,but the applications of it are limited due to the excessive computational cost.The vertex method can be employed to obtain the exact intervals of response of an uncertain problem if the interval equation can be defined as a non-convex polyhedron[Qiu,Xia and Yang(2007)],but the computational cost of it increases exponentially with the increase of the number of interval parameters.Based on the Neumann expansion and the Taylor series expansion,the interval per-turbation method(IPM)was developed[Qiu,Chen and Elishakoff(1996);Qiu and Elishakoff(1998)]for the response prediction of uncertain structures.Recently,Wu et al.[2013a,b,2014]proposed a Chebyshev inclusion function-based method to solve interval ordinary differential equation(ODE)systems and interval differential algebraic equation(DAE)systems.There is no need for the Chebyshev inclusion function-based method to obtain the explicit expression of governing equations of the uncertain systems,and the Chebyshev inclusion function-based method can control overestimation better than the Taylor inclusion function-based method in solving the interval ODE and DAE systems.

As mentioned above,the probabilistic and non-probabilistic models can be used to describe the uncertainties of uncertain systems with random parameters and uncertain systems with interval parameters,respectively.While in some engineering problems,both the random parametersand the intervalparametersare involved,and thus a hybrid analysis framework for the problems with mixed uncertainties should be constructed.Significant progress has been made in the hybrid probabilistic and interval model.Muscolino et al.(2011a,b)have investigated the stochastic interval responses of structures with uncertain-but-bounded parameters under random excitation.The reliability-based design(RBD)in static analysis of structures with random and interval parameters has been studied in literatures[Cacciola,Muscolino and Versaci(2011);Gao,Song and Tin-Loi(2010)].To analyze the response of uncertain structures with random and interval parameters,Gao et al.(2010,2011)have developed a hybrid perturbation Monte-Carlo method(HPMCM),which is derived from the MCM and the perturbation method with first-order Taylor series.Based on the HPMCM and the vertex method,the hybrid perturbation vertex method(HPVM)has been proposed for the hybrid uncertain structure-acoustic system[Xia and Yu(2013)].By employing the HPMCM and HPVM,the intervals of expectation and variance of the system response can be calculated.Compared with HPMCM,HPVM is more efficient,but the computational efficiency of HPVM decreases exponentially with the increase of the number of interval parameters.For the response analysis of low-frequency exterior acoustic fields with random and interval parameters,the hybrid perturbation method(HPM)have been proposed[Chen,Yu and Xia(2014)]recently.

As we all know,response analysis of the acoustic field with uncertain parameters has achieved great success recently.Many probabilistic methods have been developed for the prediction of the acoustic field with random parameters,such as in literatures[James and Dowling(2005,2008);Khine,Creamer and Finette(2010)].Due to the difficulty of obtaining the probability density functions of some uncertain parameters,non-probabilistic models have been employed in the response prediction ofthe uncertain acoustic field[Xia and Yu(2012,2014)].Response analysis of acoustic field with both random and interval parameters has been studied only in literature[Xia and Yu(2013)].,other literatures for this problem have not been published.Hybrid uncertain analysis methods like HPM can be considered as potential methods for the acoustic field with both random and interval parameters.

Generally speaking,although some great work has been done by researchers,study about the hybrid uncertain models is still in its primary stage.In HPMCM,HPVM,and HPM,the partial derivatives with respect to uncertain parameters should be calculated twice:one for the random parameters and the other for the interval parameters.However,the calculation of partial derivatives with respect to the interval parameters is usually complex.For the Chebyshev polynomials,there is no need to calculate the partial derivatives with respect to the interval parameters;what’s more,they have a better controlling of interval overestimation comparing with the Taylor series.By taking advantage of these merits of the Chebyshev polynomials,a new hybrid Chebyshev-perturbation method(HCPM)is proposed for the analysis of uncertain problems with random and interval parameters in this paper.In HCPM,the perturbation stochastic method based on the first-order Taylor series that accounts for the random uncertainty is integrated systematically with the Chebyshev polynomials for dealing with the interval uncertainty.At first,by treating the interval variables as constants,the random interval function is expanded with the first-order Taylor series,and the expressions of the expectation and variance can be obtained by using the random moment method;then the expectation and variance of the objective function are approximated by using the Chebyshev polynomials,and for the sake of computational efficiency,the higher order terms of Chebyshev polynomials than one are neglected;finally,the bounds of the approximate expectation and variance can be calculated by using the MCM.It is obvious that only the partial derivatives with respect to random parameters are required to be calculated in HCPM.To verify the effectiveness of HCPM,HCPM is applied to analyze the response of acoustic field with random and interval parameters.Numerical examples of a 2D u-shape acoustic tube and the 2D acoustic cavity of a van are presented to demonstrate the effectiveness of the proposed method,and as a comparison,HPM is applied to the two numerical examples,too.The numerical results prove that the accuracy of HCPM is better than that of HPM.

2 Perturbation stochastic method for functions with random parameters

The perturbation stochastic method is known as a powerful tool based on the Taylor seriesexpansion fordealing with random uncertainties.In thismethod,the function f(x)with random parameters can be approximated as the following formulation

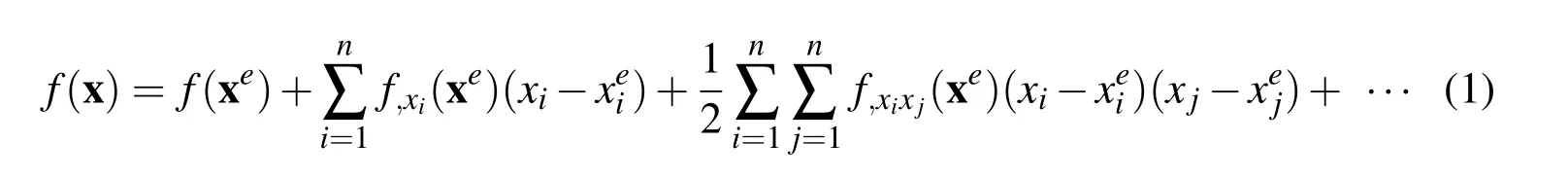
From Eq.(1),we can see that an obvious shortcoming of the perturbation stochastic method is the requirement for calculating the partial derivatives.Generally,the higher the order of the partial derivative is,the more complex the calculation of the partial derivative is,and the computational cost will increase significantly with the increase of the order of the partial derivative.What’s more,the improvement in accuracy of the higher order approximations is rather small compared with the disproportional increase of computational cost[Stefanou(2009)].Thus,the high order terms of Taylor series in Eq.(1)are usually neglected in engineering computing,and the first-and second-order stochastic methods are the most widely used.

In the conventional perturbation stochastic method,the stochastic characteristics of a random function are described as expectation and variance.For the first-order perturbation stochastic method,the expectation and variance of f(x)can be calculated by using the random moment method and can be expressed as

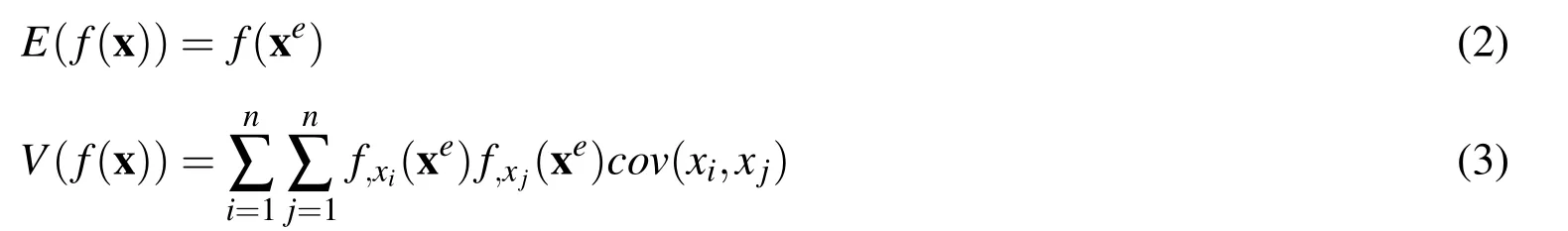
where E(·)denotes the expectation of a random variable,and V(·)denotes the variance of a random variable,cov(·)denotes the covariance of two random variables.

The second-order perturbation stochastic method can be used to calculated the expectation and variance of f(x)in a similar way if all the variables are normally distributed,and for other types of random variables,the joint probability distribution functions are required.Thus the application of the second-order perturbation stochastic method is limited in engineering practice.More information about the second-order perturbation stochastic method can be found in literature[Liu,Belytschko and Mani(1986)].

3 Chebyshev method for functions with interval parameters

The Chebyshev method is proposed for solving the interval ODE and DAE systems by Wu et al.(2013a,2013b),and the main idea of it is employing the Chebyshev polynomials to approximate the interval functions.Considering a one-dimensional interval function f(x)continuous over[a,b],which indicates that the variable x∈[a,b],the Chebyshev polynomials of degree n can be expressed as

In a similar way as the perturbation method using the Taylor series,the interval function f(x)can be approximated by using the Chebyshev polynomials

with fithe i-th constant coefficient.In the Eq.(41),if n is large enough,the interval function f(x)can be approximated with a very small error that can be neglected.The i-th constant coefficient fican be calculated by

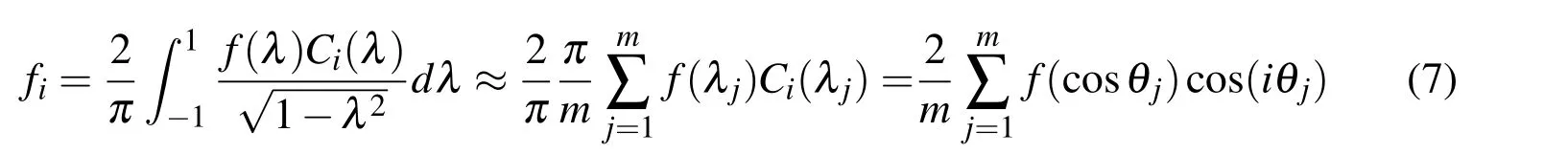
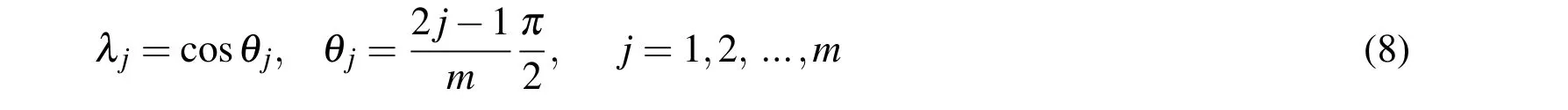
To control the integral error,m is usually set to be a value not less than n+1.

For a r-dimensional interval function f(x)continuous over[a,b],the Chebyshev polynomials of degree n can be written as

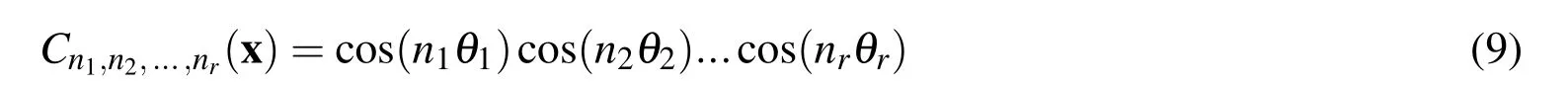
where x∈[a,b]is an interval vector consisting of r interval variables,or it can be expressed as denotes the j-th interpolation point in the integral formula,

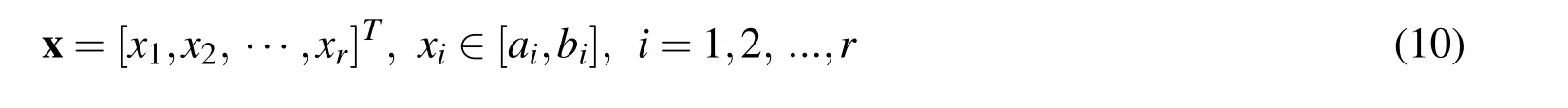
m is the total number of the interpolation points,and the expression of λjcan be written as

Similarly,the r-dimensional interval function f(x)can also be approximated by using the Chebyshev polynomials

where p is the total number of zeros occurring in the subscripts i1,...,ir.The constant coefficients fi1,...,ircan be calculated by

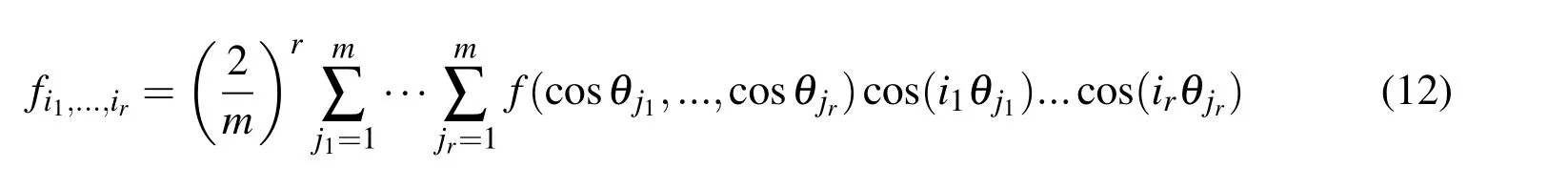
where(cosθj1,...,cosθjr)is an interpolation point,and it can be figured out from Eq.(47)that the total number of interpolation points is mr.

The purpose of the approximation using the Chebyshev polynomials is to search the bounds of the interval function effectively.For Eq.(46),different methods can be used to calculated the bounds,such as the conventional optimization algorithms,interval arithmetic and the MCM.The interval arithmetic is an efficient method to calculate the bounds,but the accuracy of it can hardly be evaluated because of the wrapping effect[Moore(1966)].Due to the robustness and simplicity of MCM,the MCM will be employed to calculated the bounds of the function approximated by Chebyshev polynomials in this paper.

4 HCPM for functions with random and interval parameters

In this section,the first-order perturbation stochastic method is integrated with the first-order Chebyshev method to deal with the functions with random and interval parameters,and the hybrid Chebyshev-perturbation method(HCPM)is proposed.Consider a random interval function f(xR,xI),where xR=[xR1,xR2,···xRn]Tis the random vector,xI=[xI1,xI2,···xIr]Tis the interval vector.The expectation and variance of xRcan be expressed as

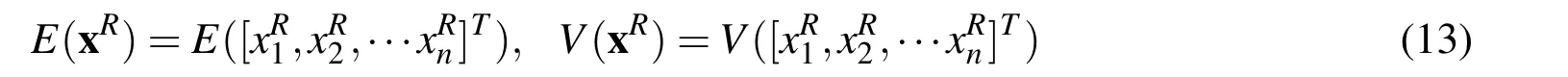
The interval of xIcan be expressed as

By treating the interval variables as constants,f(xR,xI)can be approximated by using the first-order Taylor series at the expectations of the random variables,which is expressed as

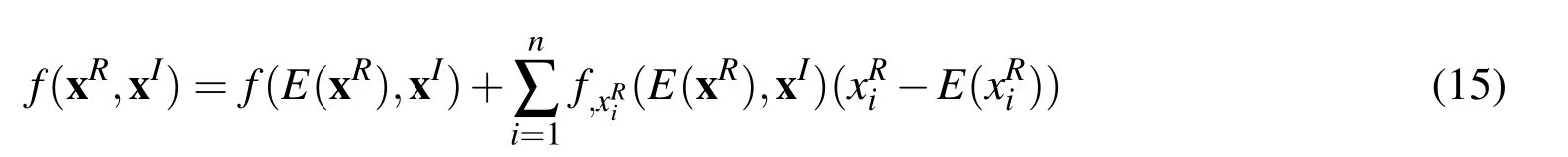
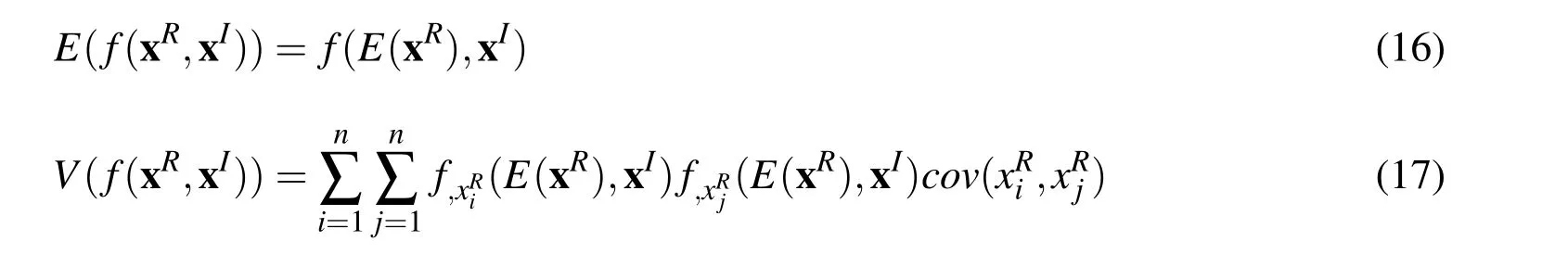
It can be seen from Eqs.(16)and(17)that the expectation and variance of f(xR,xI)are expressed as functions with respect to the interval variables,thus E(f(xR,xI))and V(f(xR,xI))are also interval variables and can be rewritten as

The intervals of E F(xI)and V F(xI)can be calculated by different methods,such as the IPM and the Chebyshev method.If the IPM is employed,the hybrid uncertain analysis method turns to be the HPM,which was proposed by Chen et al in literature[Chen,Yu and Xia(2014)].As the HPM is used,it should be noted that the calculation of partial derivatives of the variance expressed in Eq.(17)is very complex,which can be considered as a shortcoming of HPM.In this paper,the Chebyshev method is used to calculated the intervals of E F(xI)and V F(xI),and the hybrid method turns to be the HCPM.Compared with HPM,there is no need for HCPM to calculate the complex partial derivatives of the variance expressed in Eq.(17).

According to Eq.(11),E F(xI)and V F(xI)can be approximated by using the Chebyshev polynomials

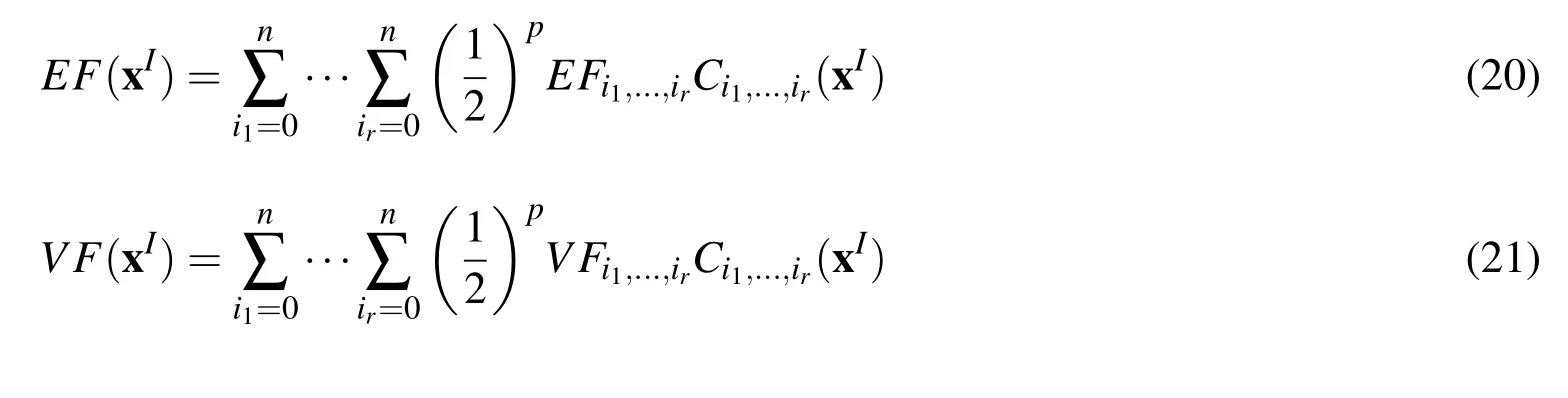
where E Fi1,...,irand V Fi1,...,irare the constant coefficient,and they can be calculated by using Eq.(12)as follows

From Eqs.(20)～(23),we can see that E F(xI)and V F(xI)are the sum of(n+1)rterms,E Fi1,...,irand V Fi1,...,irare the sum of mrterms,and given that m is a parameter not less than n+1,it is foreseeable that the computational cost of the Chebyshev method will increase exponentially with the increase of the order n.Therefore,for the sake of computational efficiency,higher order terms of the Chebyshev polynomials than one are neglected and the value of m is set to be n+1 in this paper.Thus,Eqs.(20)and(21)can be rewritten as

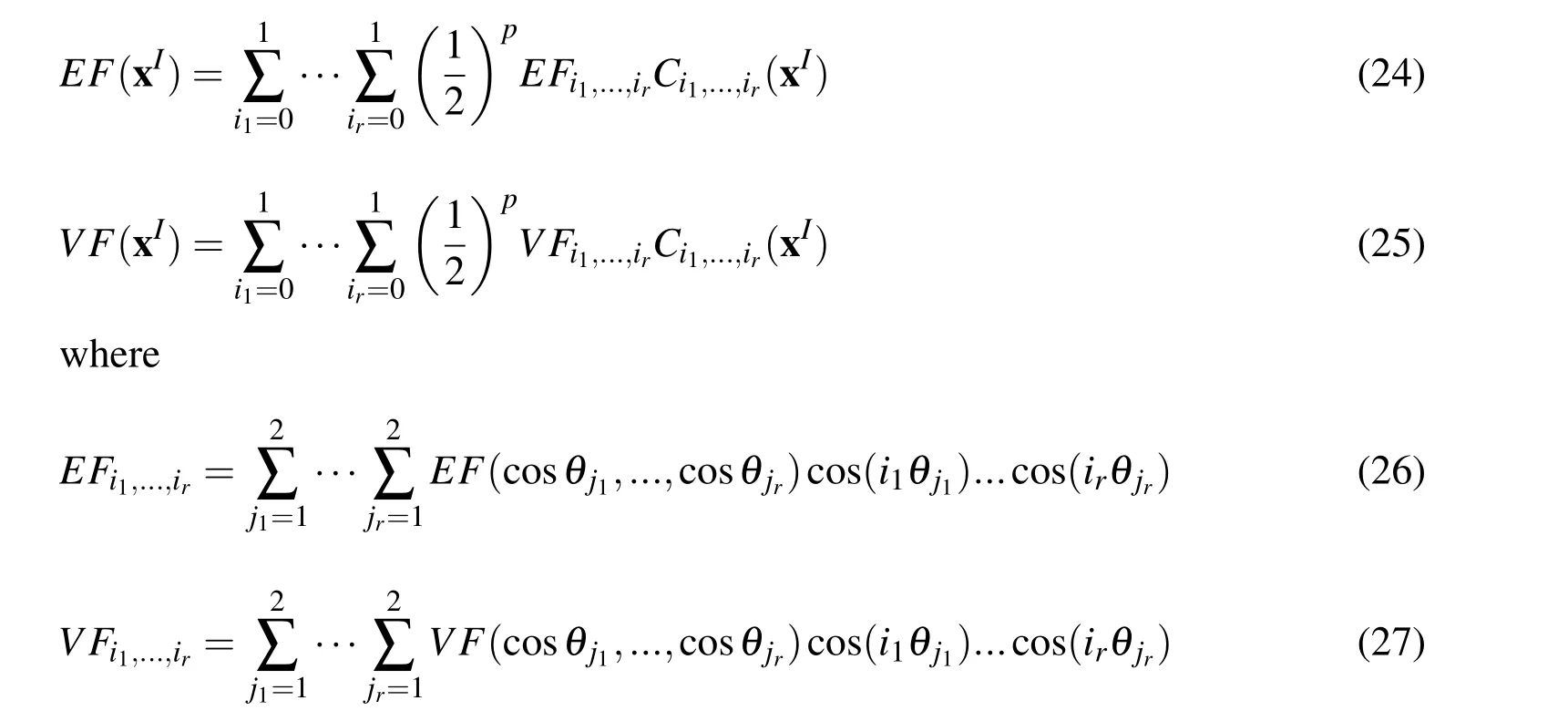
By applying the MCM to Eqs.(24)and(25),the lower and upper bounds of E F(xI)and V F(xI)can be calculated and are expressed as

Due to the neglect of higher order terms of the Taylor series and the Chebyshev polynomials,it should be noted that the application of HCPM is limited to the analysis of uncertain problem with small parametric uncertainty.However,many uncertain problems in engineering practice meet with the condition that there are only small fluctuations of uncertain parameters.Thus,HCPM is applicable.

One Simple Example.Considering a random interval functionf(x,y)=x2+xy2,wherex∈[0.6,1.4],y～N(1,0.12),HPM and HCPM are employed to calculate the intervals of the expectation and variance off(x,y).The intervals calculated by HPM are

The intervals calculated by HCPM are

The actual intervals of the expectation and variance off(x,y)are

From Eqs(30)～(32),we can see that the intervals yielded by HCPM match the actualintervals more closely than that yielded by HPM,which indicates thatHCPM has an advantage in accuracy over HPM.

The main steps of HCPM for uncertain problems with random and interval parameters can be summarized as follows

Step 1:Expand the random interval functionf(xR,xI)with the first-order Taylor series at the expectations of the random variables(Eq.(15)).

Step 2:Express the expectation and variance of the expanded function off(xR,xI)as functions with respect to the interval variables by using the random moment method(Eqs.(16)and(17)).

Step 3:Approximate the expectation and variance in Step 2 with the first-order Chebyshev polynomials(Eqs.(24)and(25)).

Step 4:Calculate the bounds of the approximated expectation and variance in Step 3 by using the MCM.

5 Prediction of the acoustic field with random and interval parameters

As is known to all,traditional uncertain approaches for the uncertain acoustic problems are probabilistic methods;the non-probabilistic model has been introduced into the uncertain acoustic problems by Xia et al.(2012,2014)recently.However,due to the unpredictable external loads and the effects of the aggressive environmental factors,it is possible for acoustic field to possess both the probabilistic and non-probabilistic parameters.Thus the analysis of acoustic field with hybrid uncertain parameters is meaningful.In this section,the HCPM is applied to the acoustic field with random and interval parameters,and the corresponding equations are derived.

5.1 Basic dynamic equilibrium equation of an acoustic cavity

Fig.1 is a simple diagram of an acoustic cavity ?,where ΓDdenotes the Dirichlet boundary condition,ΓNdenotes the Neumann boundary condition,ΓRdenotes the Robin boundary condition.The steady-state sound pressure p in the frequency domain can be expressed by using the Helmholtz equation

where?2is the Laplace operator;k=ω/c is the wave number,and ω denotes the angular frequency,c denotes the sound speed.

The initial boundary conditions of ΓD,ΓNand ΓRcan be expressed as

From Eqs(33)～(36),the dynamic equilibrium equation of an acoustic cavity modeled by the finite element method can be obtained and expressed as

where F represents the load vector,p is the sound pressure vector,Z=K?k2M+jk C is the dynamic stiffness matrix of the acoustic cavity,in which K,M,C represent the stiffness matrix,mass matrix,and the damping matrix,respectively.K,M,C,F can be expressed as follows

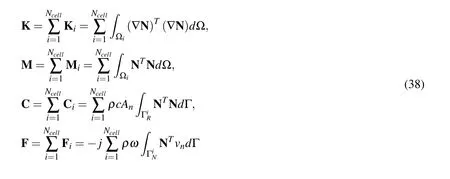
Figure 1:An acoustic cavity ?.

5.2 Acoustic dynamic equilibrium equation with random and interval parameters

When the random and interval parameters are introduced into the acoustic dynamic equilibrium equation,Eq.(37)can be rewritten as

where xRis the random vector consisting of n random variables,xIis the interval vector consisting of r interval variables.

By treating the interval variables as constants and employing the first-order Taylor series,the random interval dynamic stiffness matrix Z(xR,xI)and the random interval load vector F(xR,xI)can be expanded at the expectations of the random variables,and they can be expressed as

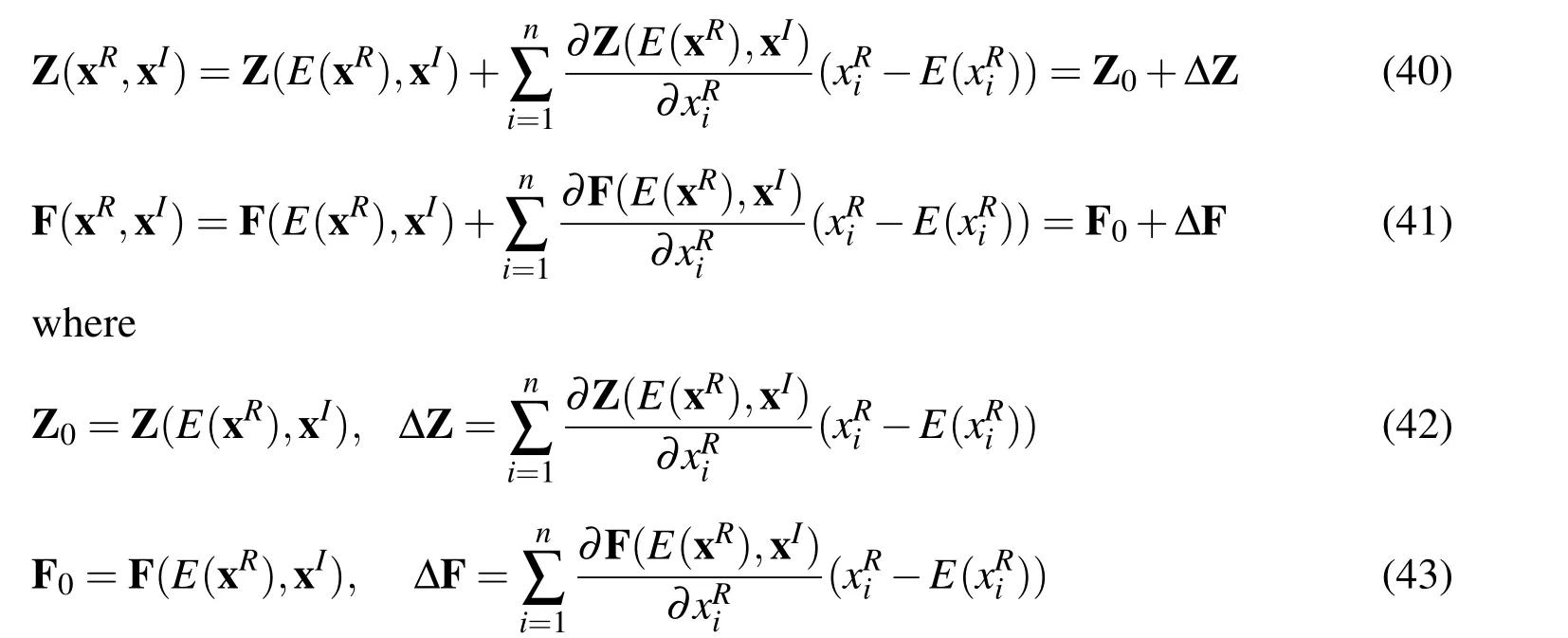
Substitute Eqs(40)and(41)into Eq.(39)and use some simple mathematics,one can get

If the spectral radius of(Z0)?1?Z is less than 1,(Z0+?Z)?1can be expanded by employing the Neumann series

Thus,Eq.(44)can be expressed as

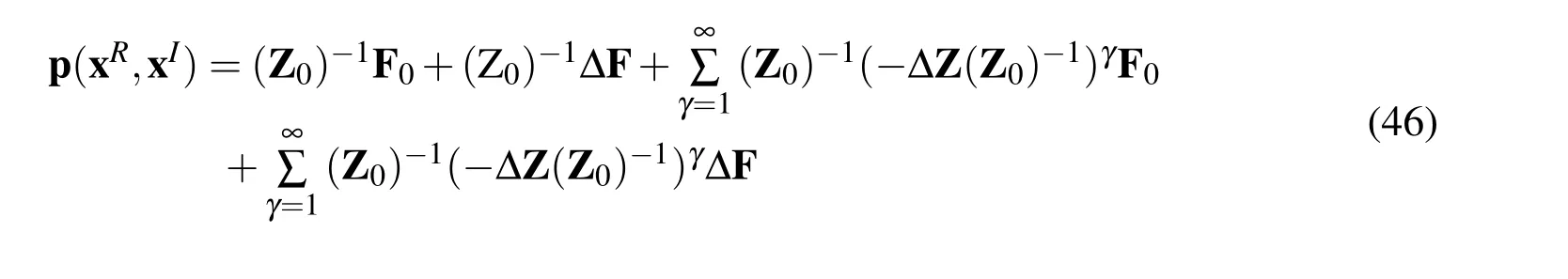
By neglecting the higher-order terms,Eq.(46)can be rewritten as

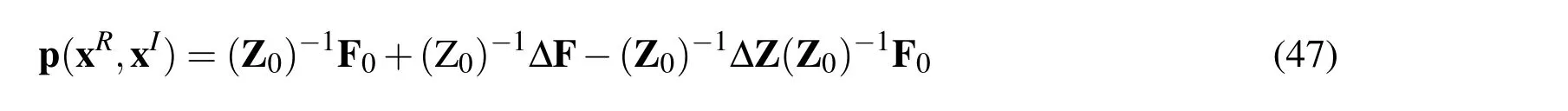
Substitute Eqs(42)and(43)into Eq.(47)and use some simple mathematics,one can get

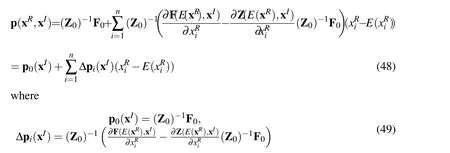
By applying the random moment method to Eq.(48),the expectation and variance of p(xR,xI)can be obtained and expressed as

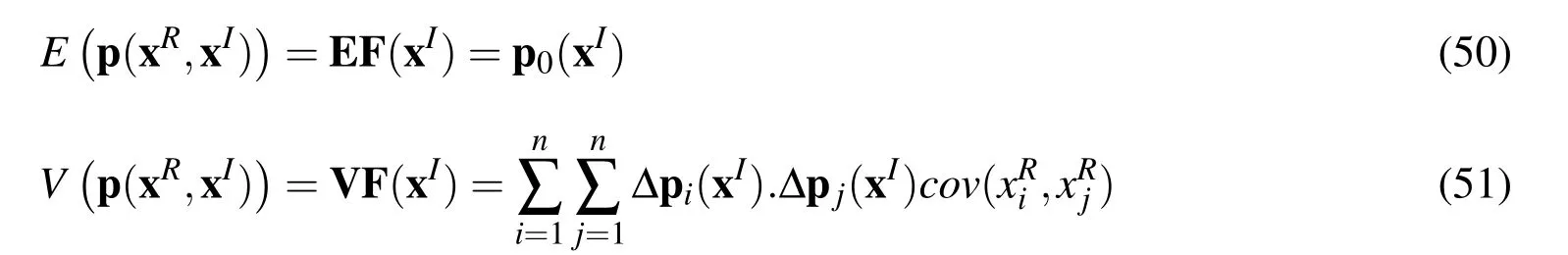
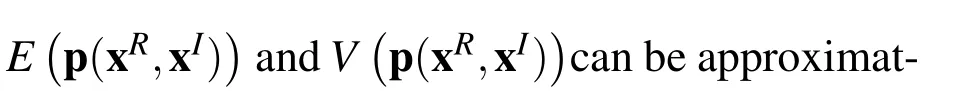
By applying the MCM to Eqs.(52)and(53),the lower and upper bounds of expectation and variance of p(xR,xI)can be calculated and expressed as

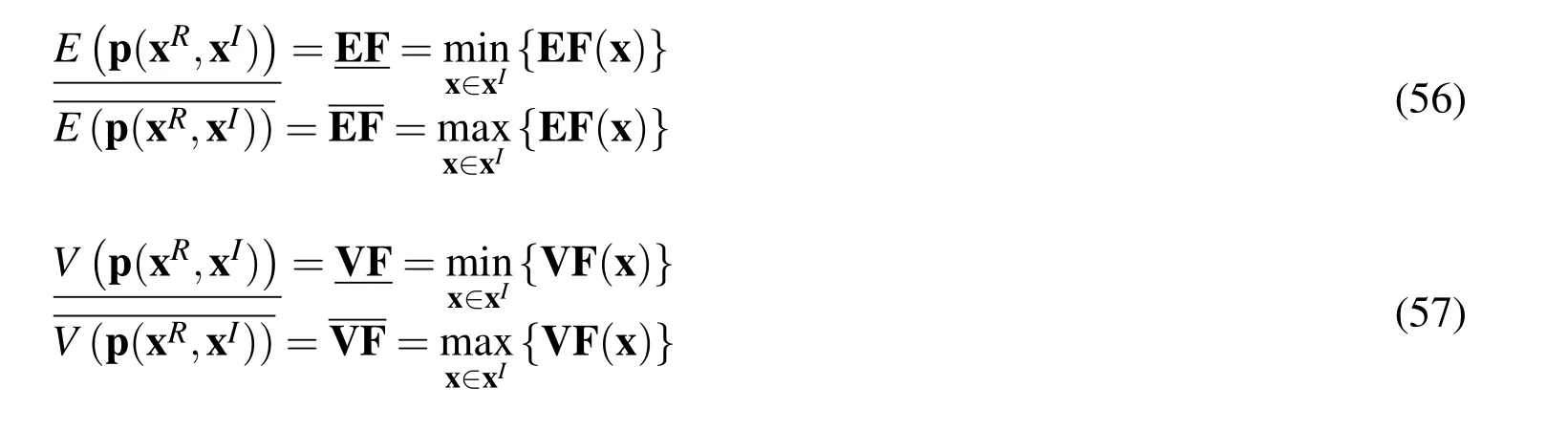
5.3 Numerical analysis of a 2D u-shape acoustic tube

A 2D u-shape acoustic tube depicted in Fig.2 is considered.The u-shape acoustic cavity is filled with air,and the diameter of the circular cross-section is 0.1 m.A discontinuous normal velocity excitation vnis loaded on the left top side of the u-shape tube,and other edges are treated as perfectly rigid.The u-shape tube is modeled by the FEM with 136 quadrilateral elements and 175 nodes.Points 1～35 are located along the central axis of the u-shape tube model.

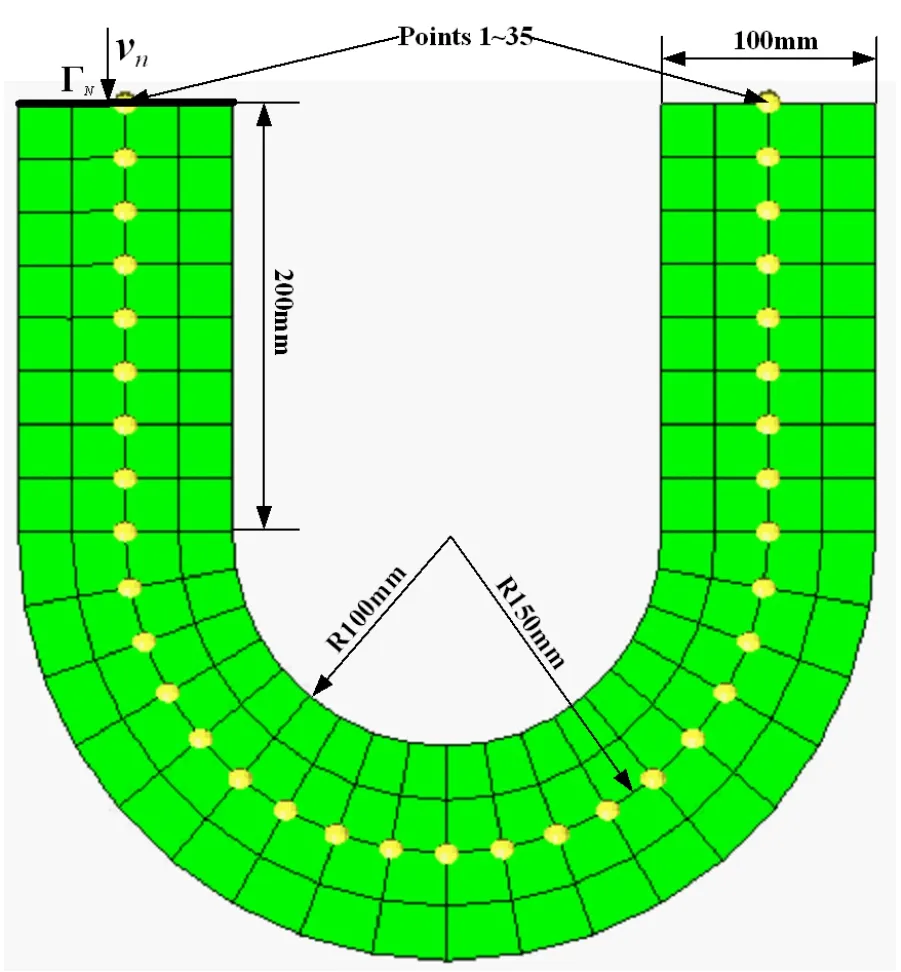
Figure 2:The 2D u-shape acoustic tube.

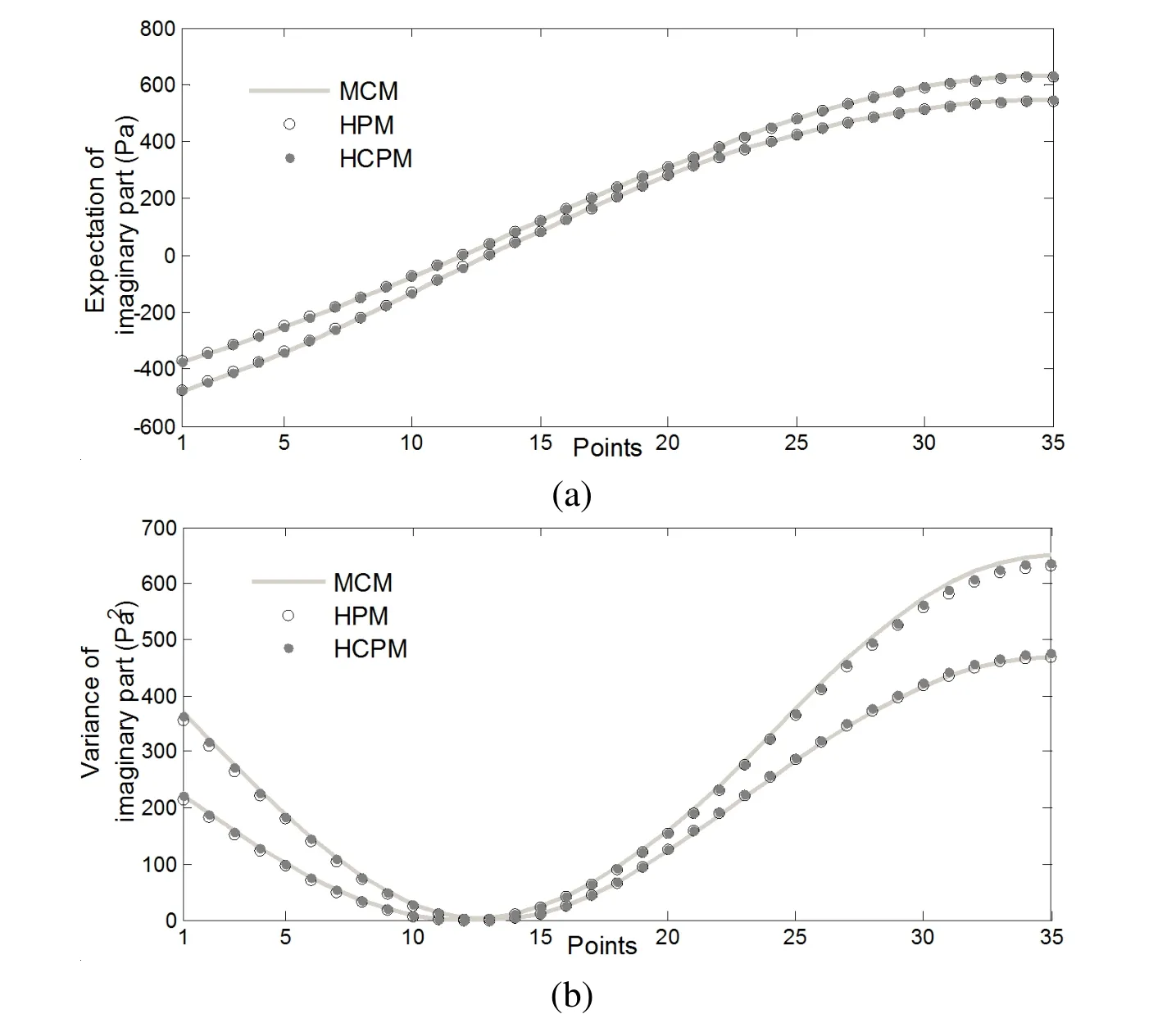
Figure 3:The lower and upper bounds of expectation and variance of the sound pressure’s imaginary part along the central axis(f=150 Hz):(a)expectation;(b)variance.

Considering the uncertainty in the properties of the air caused by the changes of environment temperature,the sound speed c and the density ρ of air are treated as interval uncertain parameters.The interval of the sound speed c is set to be[334.3,349.1],and the interval of the density ρ of air is set to be[1.164,1.269].The discontinuous normal velocity excitation vnis considered as a random parameter normally distributed,whose expectation is 0.1m/s,and the coefficient of variation is 4%.

All simulations about this u-shape tube model are carried out by using MATLAB R2014a on a 3.60 GHz Intel(R)Core(TM)CPU i7-4790.The lower and upper bounds of expectation and variance of the sound pressure at the points 1～35 are calculated by using HCPM and HPM,and the reference results are obtained by using the Monte Carlo method(MCM).In the Monte Carlo simulation,104sam-ples of the random parameter are firstly conducted to calculate the expectation and variance,103samples of the interval parameters are then conducted to calculate the lower and upper bounds of the expectation and variance.Thus,the total number of samples to get the reference results is 107.The lower and upper bounds of expectation and variance of the sound pressure’s imaginary part at the points 1～35 are shown in Fig.3 for frequency f=150Hz,Fig.4 for frequency f=250Hz,Fig.5 for frequency f=350Hz.It can be found from Figs.3～5 that the bounds of expectation yielded by HCPM and HPM match the reference bounds perfectly,and the bounds of variance yielded by HCPM match the reference bounds more closely than that yielded by HPM.

To investigate the accuracy of HCPM and HPM for the prediction of acoustic field with random and interval parameters more clearly,the global error is defined as

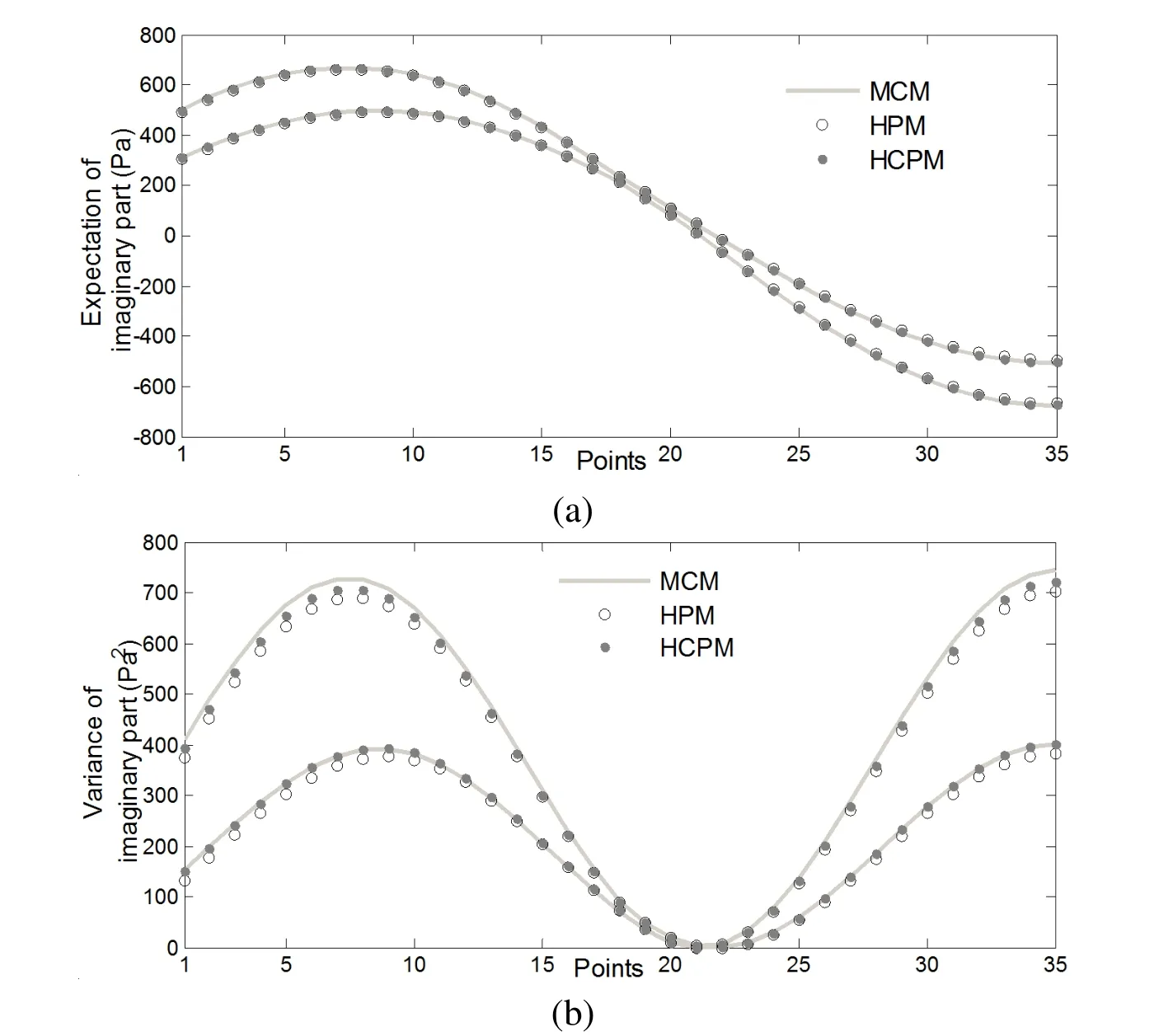
Figure 4:The lower and upper bounds of expectation and variance of the sound pressure’s imaginary part along the central axis(f=250 Hz):(a)expectation;(b)variance.

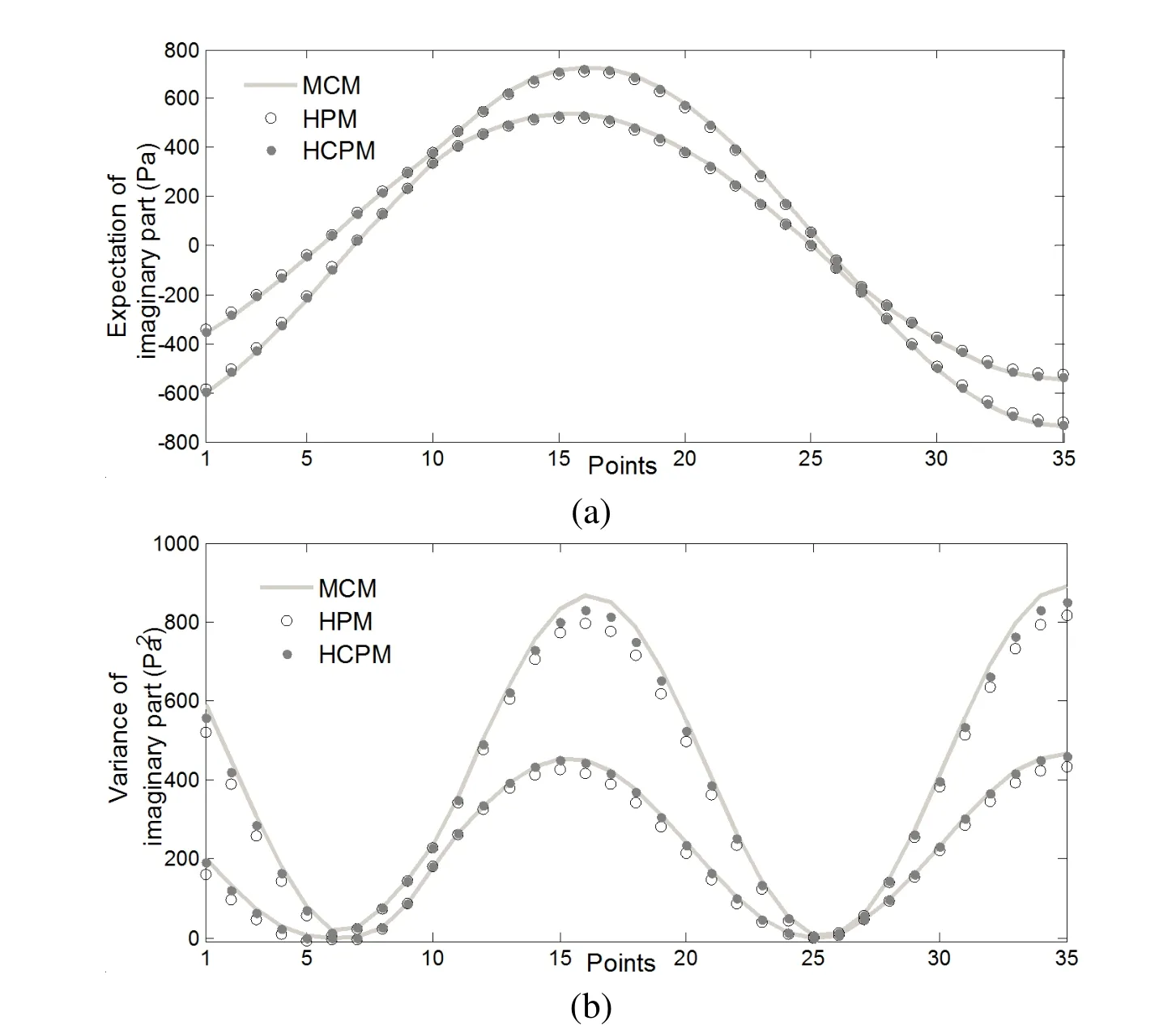
Figure 5:The lower and upper bounds of expectation and variance of the sound pressure’s imaginary part along the central axis(f=350 Hz):(a)expectation;(b)variance.

where GE represents the global error,fMrepresents the result calculated by MCM,fHrepresents the result calculated by HCPM or HPM.

On the central axis,the global errors of the bounds of expectation and variance of the sound pressure’s imaginary part are calculated and listed in Table 1,the considered frequency is 250Hz.In Table 1,“LB”denotes the lower bounds,and“UB”denotesthe upperbounds.Itcan be seen from Table 1 thatthe globalerrorsof the results calculated by HCPM and HPM are both acceptable;the global errors of the expectations are smaller than that of the variances,which is mainly because of the relation between the variance and the square of expectation;the global errors of HCPM are smaller than that of HPM,thus we can get that HCPM has an advantage over HPM in accuracy for the prediction of acoustic field with random and interval parameters.

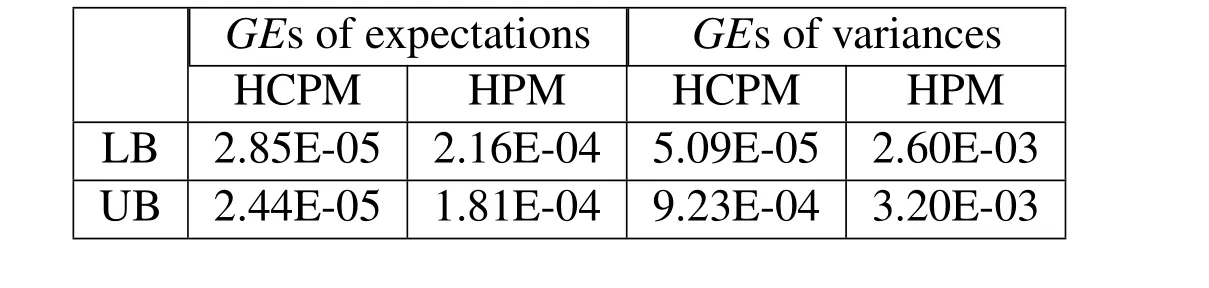
Table 1:The global errors of the bounds of expectation and variance of the sound pressure’s imaginary part on the central axis(f=250Hz).

To further investigate the accuracy of HCPM and HPM for the prediction of acoustic field with random and interval parameters,we increase the fluctuation of the uncertain parameters.The intervals of sound speed c and air density ρ are set to be[325.2,357.5]and[1.110,1.342],respectively.The expectation of the normally distributed velocity excitation vnis 0.1m/s,and the coefficient of variation is set to be 8%.Fig.6 shows the lower and upper bounds of expectation and variance of the sound pressure’s imaginary part at the points 1～35,the considered frequency is 250Hz.It can be seen from Fig.6 that the bounds of the expectation and variance calculated by HPM deviate from the reference bounds seriously,while the bounds of the expectation and variance calculated by HPCM still match the reference bounds well.Thus,we can conclude that HCPM can achieve higher accuracy than HPM for the prediction of acoustic field with larger parametric uncertainties.

As previously stated,due to the neglect of higher order terms of the Taylor series and the Chebyshev polynomials,although the HCPM can achieve better accuracy than HPM,the application of HCPM is still limited to the analysis of uncertain problem with small parametric uncertainty.For the analysis of uncertain problem with large parametric uncertainty,the higer order terms of the Taylor series and the Chebyshev polynomials are available.

5.4 Numerical analysis of the 2D acoustic cavity of a van

The prediction of interior acoustic field of a vehicle is a hotspot issue in the research field ofvehicle engineering.Numericalresultsforthe prediction ofinterioracoustic field can provide valuable information for the optimization of noise in the vehicle.Fig.7 illustrates the 2D conceptual acoustic cavity model of a van with dimensions 2969×1493 mm.The acoustic cavity is filled with air,and it is modeled by FEM with 260 quadrilateral elements and 318 nodes.Considering the changes of environment temperature,the sound speed c and the density ρof air are treated as interval uncertain parameters,and the intervals of them are[331.3,346.1]and[1.184,1.293],respectively.A discontinuous and normally distributed velocity excitation vnis imposed on the front bottom of the acoustic cavity.The expectation of vnis 0.1m/s,and the coefficient of variation is 4%.The admittance coefficient Analong the Robin boundary ΓRat the front windshield is also considered as a normally distributed parameter,and the expectation of it is 0.0015m/Pa.s,the coefficient of variation is 4%.Points 1～10 are located near the driver and passenger.

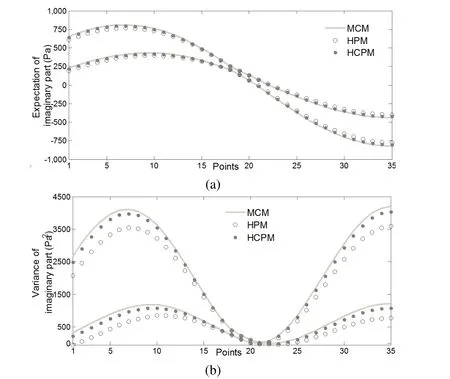
Figure 6:The lower and upper bounds of expectation and variance of the sound pressure’s imaginary part along the central axis(f=250 Hz,with larger-fluctuation uncertain parameters):(a)expectation;(b)variance.

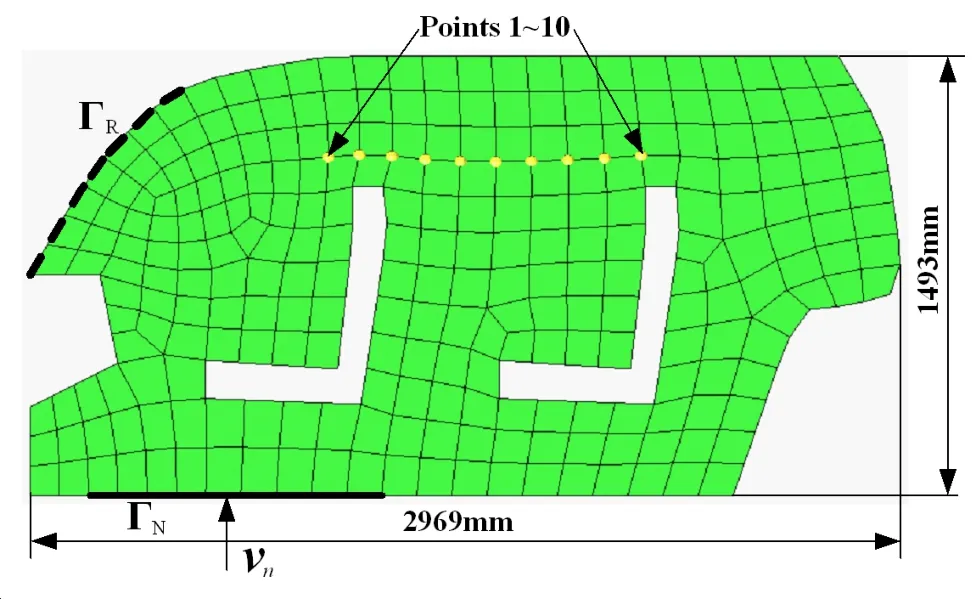
Figure 7:The 2D acoustic cavity model of a van.

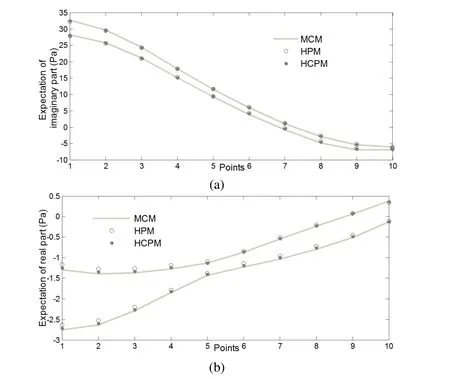
Figure 8:The lower and upper bounds of expectation of the sound pressure’s imaginary and real part at points 1～10(f=150 Hz):(a)imaginary part;(b)real part.

In thisnumericalexample,allsimulationsare carried outby using MATLAB R2014a on a 3.60 GHz Intel(R)Core(TM)CPU i7-4790.The bounds of expectation and variance of the sound pressure’s real and imaginary parts at points 1～10 are calculated by using HPM and HCPM,reference results are obtained with Monte Carlo simulation.In the Monte Carlo simulation,104samples of the random parameters are conducted to calculate the expectation and variance,and 103samples of the interval parameters are conducted to calculate the bounds of the expectation and variance,thus the total number of samples is 107.The lower and upper bounds of expectation and variance of the sound pressure’s real and imaginary parts at points 1～10 are shown in Figs.8 and 9,respectively;the considered frequency is 150 Hz.It can be seen from Figs.8(a)and 9(a)that the bounds of the expectation and variance of the sound pressure’s imaginary part calculated by the two methods match the reference bounds very well.From Fig.8(b),we can see that the bounds of the expectation of the sound pressure’s real part calculated by HCPM match the reference bounds more closely than that calculated by HPM;from Fig.9(b),we can see that the bounds of the variance of the sound pressure’s real part calculated by HPM significantly deviate from the reference bounds,while the bounds of the variance of the sound pressure’s real part calculated by HCPM are still in good agreement with the reference bounds;thus we can conclude that HCPM has achieved more excellent accuracy than HPM.Comparing Figs 8(a)and 9(a)with Figs.8(b)and 9(b),we can figure out that the bounds of the expectation and variance of the sound pressure’s real part calculated by the two methods show perfect agreement with their reference bounds,while the bounds of the expectation and variance of the sound pressure’s imaginary part calculated by the two methods show relatively mediocre agreement with their reference bounds,which may be because that the modules of the sound pressure’s imaginary part are much smaller than that of the sound pressure’s real part,and the corresponding relative errors become much larger.

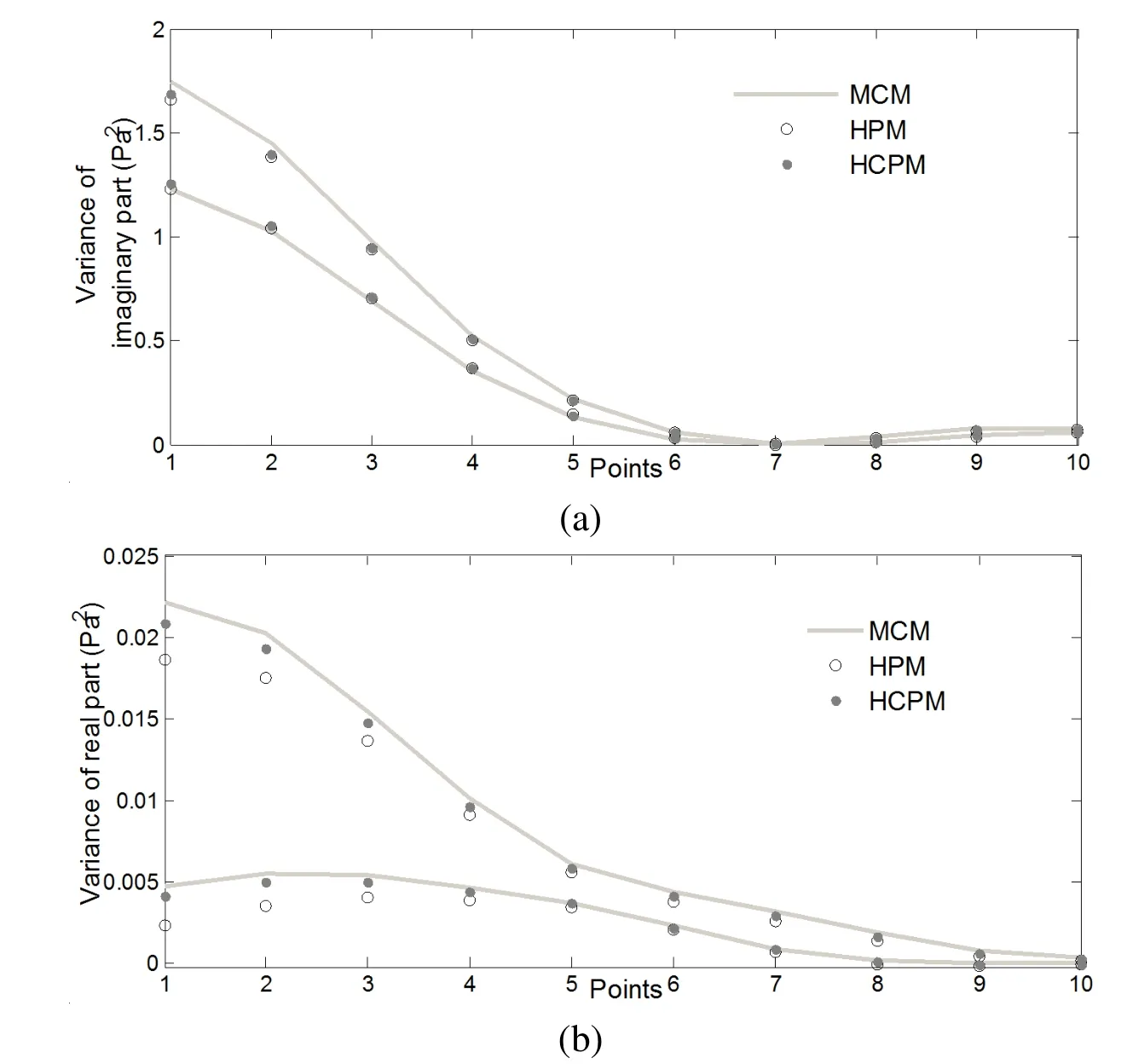
Figure 9:The lower and upper bounds of variance of the sound pressure’s imaginary and real part at points 1～10(f=150 Hz):(a)imaginary part;(b)real part.

The computational efficiency is also an important index for evaluating the numerical methods’performances.Execution times of HCPM and HPM for calculating the expectation and variance of the sound pressure atpoints 1～10 are listed in Table 2,the considered frequency is 150Hz.It can be seen from Table 2 that the execution times of HCPM is a bit longer than that of HPM,but considering the improvement in accuracy and the excessive computational cost of MCM,the additional computational cost of HCPM is acceptable.

Table 2:Execution times to calculate the expectation and variance.

6 Conclusions

In this paper,a new hybrid uncertain analysis method termed as hybrid Chebyshevperturbation method(HCPM)is proposed for the uncertain problems involving random and interval parameters.In HCPM,the perturbation method based on the first-order Taylor series is employed to deal with the random uncertainty,while the first-order Chebyshev polynomials is used to deal with the interval uncertainty,and they are integrated systematically.Speci fically,a response function of the uncertain system is firstly expanded with the first-order Taylor series by considering the interval variables as constants,and the random moment method is applied to the expanded function for obtaining the expressions of the expectation and variance;then by using the first-order Chebyshev polynomials,the expectation and variance of the function are approximated;by applying the Monte Carlo simulation to the expressions of the expectation and variance approximated with the first-order Chebyshev polynomials,the bounds of the expectation and variance are finally calculated.

The proposed method is demonstrated by application to a 2D u-shape acoustic tube and the 2D acoustic cavity of a van with random and interval parameters;as a comparison,HPM is applied to the two numerical examples,too;the Monte Carlo method is employed to yield the reference results.Numerical results verify that the accuracy of HCPM is better than that of HPM.The computational efficiency of HCPM is a bit lower than that of the HPM,but the additional computational cost is acceptable considering the excessive computational cost of MCM.It should be pointed out that the application of HCPM is limited to the analysis of uncertain problems with small parametric uncertainty,because only the first-order terms of the Taylor series and the Chebyshev polynomials are considered.For the analysis of uncertain problem with large parametric uncertainty,the higer order terms of the Taylor series and the Chebyshev polynomials should be considered.

Acknowledgement:The paper is supported by National Natural Science Foundation of China(No.11402083),Independent Research Projects of State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body in Hunan University(Grant No.734215002,No.51375002).

Cacciola,P.;Muscolino,G.;Versaci,C.(2011b):Deterministic and stochastic seismic analysis of buildings with uncertain-but-bounded mass distribution.Computers&Structures,vol.89,pp.2028–2036.

?avdar,?.;Bayraktar,A.;?avdar,S.;Adanur,A.(2008):Perturbation based stochastic finite element analysis of the structural systems with composite sections under earthquake forces.Steel and Composite Structures,vol.8,pp.129–144.

Chen,N.Z.;Soares,C.G.(2008):Spectral stochastic finite element analysis for laminated composite plates.Computer Methods in Applied Mechanics and Engineering,vol.197,pp.4830–4839.

Chen,N.;Yu,D.;Xia,B.(2014):Hybrid uncertain analysis for the prediction of exterior acoustic field with interval and random parameters.Computers&Structures,vol.141,pp.9–18.

Chung,D.B.;Gutiérrez,M.A.;Graham-Brady,L.L.;Lingen,F.J.(2005):Efficient numerical strategies for spectral stochastic finite element models.International Journal for Numerical Methods in Engineering,vol.64,pp.1334–1349.

Fishman,G.S.(1996):Monte Carlo:Concepts,Algorithms,and Applications.Springer-Verlag,New York.

Gao,W.;Song,C.;Tin-Loi,F.(2010):Probabilistic interval analysis for structures with uncertainty.Structural Safety,vol.32,pp.191–199.

Gao,W.;Song,C.;Tin-Loi,F.(2010):Static response and reliability analysis of structural systems with random and interval properties.IOP Conference.Series.Material.Science.Engineering,vol.10,pp.012200.1–012200.10.

Gao,W.;Wu,D.;Song,C.;Tin-Loi,F.;Li,X.(2011):Hybrid probabilistic interval analysis of bar structures with uncertainty using a mixed perturbation Monte-Carlo method.Finite Elements in Analysis and Design,vol.47,pp.643–652.

Hua,J.;Qiu,Z.(2010):Non-probabilistic convex models and interval analysis method for dynamic response of a beam with bounded uncertainty.Applied Mathematical Modelling,vol.34,pp.725–734.

Hurtado,J.E.;Barbat,A.H.(1998):Monte Carlo techniques in computational stochastic mechanics.Archives of Computational Methods in Engineering,vol.5,pp.3–29.

James,K.R.;Dowling,D.R.(2005):A probability density function method for acoustic field uncertainty analysis.Journal of the Acoustical Society of America,vol.118,pp.2802–2810.

James,K.R.;Dowling,D.R.(2008):A method for approximating acoustic-fieldamplitude uncertainty caused by environmental uncertainties.Journal of the A-coustical Society of America,vol.124,pp.1465–1476.

Jiang,C.;Bi,R.;Lu,G.;Han,X.(2013):Structural reliability analysis using non-probabilistic convex model.Computer methods in applied mechanics and engineering,vol.254,pp.83–98.

Khine,Y.Y.;Creamer,D.B.;Finette,S.(2010):Acoustic propagation in an uncertain waveguide environment using stochastic basis expansions.Journal of Computational Acoustics,vol.18,pp.397–441.

Kaminski,M.M.(2010):Ageneralized stochastic perturbation technique for plasticity problems.Computational Mechanics,vol.45,pp.349–361.

Kami′nski,M.;Lauke,B.(2013):Parameter sensitivity and probabilistic analysis of the elastic homogenized properties for rubber filled polymers.Computer Modeling in Engineering&Sciences,vol.93,no.6,pp.411–440.

Li,F.;Luo,Z.;Rong,J.;Hu,L.(2013):A non-probabilistic reliability-based optimization of structures using convex models.Computer Modeling in Engineering&Sciences,vol.95,no.6,pp.453–482.

Liu,W.K.;Belytschko,T.;Mani,(1986):A.Probabilistic finite elements for nonlinear structural dynamics.Computer methods in applied mechanics and engineering,vol.56,pp.61–86.

Moore,R.E.(1966):Interval analysis.Englewood Cliffs,New Jersey:Prentice-Hall.

Muscolino,G.;Sof i,A.(2011a):Response statistics of linear structures with uncertain-but-bounded parameters under Gaussian stochastic input.International Journal of Structural Stability and Dynamics,vol.11,pp.775–804.

Shang,S;Yun,G.J.(2013):Stochastic?nite element with material uncertainties:implementation in a general purpose simulation program,Finite Elements in Analysis and Design,vol.64,pp.65–78.

Stefanou,G.(2009):The stochastic finite element method:past,present and future.Computer Methods in Applied Mechanics and Engineering,vol.198,pp.1031–1051.

Wu,J.;Zhang,Y.;Chen,L.;Luo,Z.(2013a):A Chebyshev interval method for nonlinear dynamic systems under uncertainty.Applied Mathematical Modelling,vol.37,pp.4578–4591.

Wu,J.;Luo,Z.;Zhang,Y.;Zhang,N.;Chen,L.(2013b):Interval uncertain method for multibody mechanical systems using Chebyshev inclusion functions.International Journal for Numerical Methods in Engineering,vol.95,pp.608–630.

Wu,J.;Luo,Z.;Zhang,Y.;Zhang,N.(2014):An interval uncertain optimization method for vehicle suspensions using Chebyshev metamodels.Applied Mathematical Modelling,vol.38,pp.3706–3723.

Wang,J.;Qiu,Z.(2010):The reliability analysis of probabilistic and interval hybrid structural system.Applied Mathematical Modelling,vol.34,pp.3648–3658.

Xia,B.;Yu,D.(2013):Hybrid uncertain analysis for structural-acoustic problem with random and interval parameters.Journal of Sound and Vibration,vol.332,pp.2701–2720.

Xia,B.;Yu,D.(2012):Interval analysis of acoustic field with uncertain-butbounded parameters.Computers&Structures.vol.112–113,pp.235–244.

Xia,B.;Yu,D.(2014):Response analysis ofacoustic field with convex parameters.Journal of Vibration and Acoustics,vol.136,pp.041017.1–041017.12.

Xia,B.;Yu,D.;Liu,J.(2013):Probabilistic interval perturbation methods for hybrid uncertain acoustic field prediction,Journal of Vibration and Acoustics,vol.135,pp.021009.1–021009.12.

1State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,Hunan University,Changsha,Hunan,People’s Republic of China,410082.

2Corresponding author.Tel.:+86 073188821915;fax:+86 073188823946;

E-mail:djyu@hnu.edu.cn