E ff ect of Mis fit Strain on Pyroelectric Properties of(111)Oriented Pb(Zr1?xTix)O3 Thin Films?
Jian-Hua Qiu(邱建華)? Zhi-Hui Chen(陳智慧)Xiu-Qin Wang(王秀琴)Ning-Yi Yuan(袁寧一) and Jian-Ning Ding(丁建寧)
1Jiangsu Province Cultivation base for State Key Laboratory of Photovoltaic Science and Technology,Changzhou University,Changzhou 213164,China
2Jiangsu Collaborative Innovation Center of Photovolatic Science and Engineering,Changzhou University,Changzhou 213164,China
3School of Material Science and Engineering,Jiangsu University,Zhenjiang 212013,China
1 Introduction
During the past decades,ferroelectric thin films have attracted great attention for a variety of device applications in nonvolatile ferroelectric memories,piezoelectric sensors,and pyroelectric detectors.[1?3]Among the ferroelectric families,Pb(Zr1?xTix)O3thin films are the most investigated system due to their high dielectric constants,remarkable piezoelectric and pyroelectric properties,especially for the Ti composition around the morphotropic phase boundary(MPB).[4?6]The physical properties are strongly dependent on the Ti composition and if lm orientation.[7]The(001)orientedthin films were widely studied because of their outstanding properties,however,researchers paid less attention to the physical properties of(111)oriented films.
Experimentally,perfectly oriented(001),(101),and(111)Pb(Zr1?xTix)O3thin films were grown on identical(111)CaF2substrates by metal organic chemical vapor deposition.[8]The saturation polarizationsPsatfor(001),(101),and(111)oriented Pb(Zr0.5Ti0.5)O3thin films were 75,50,and 43μC/cm2,respectively.Similar to the ferroelectricity,the piezoelectric and pyroelectric properties of(111)oriented Pb(Zr1?xTix)O3thin films were smaller than that of(001)oriented films.Epitaxial Pb(Zr1?xTix)O3thin films were deposited on Nbdoped SrTiO3monocrystalline substrates.[9]The tetragonal(001)Pb(Zr1?xTix)O3thin films on(001)Nb:SrTiO3 substrates exhibited higher piezoelectric coefficientd33than the rhombohedral(111)oriented films on(111)Nb:SrTiO3substrates.In addition,(001)and(111)oriented Pb(Zr1?xTix)O3thin films were fabricated epitaxially on Pt/γ–Al2O3/Si substrates and the Ti composition dependence of pyroelectric property was investigated.[10]The maximal pyroelectric coefficients of(001)and(111)oriented Pb(Zr1?xTix)O3thin films were obtained for the Ti composition near the MPB with values of 1.8×10?4C/m2K and 1.4×10?4C/m2K for(001)and(111)oriented films respectively.
Although(111)oriented films showed the low values of physical properties,they can be enhanced by controlling the Ti composition and film thickness.[9,11?15]As a matter of fact,mis fit strain originated from the lattice mismatch between the film and substrate plays an important role in adjusting the physical properties,so called“strain engeering”.The Effect of mis fit strain on the dielectric and piezoelectric properties was investigated theoretically for single domain(001)oriented Pb(Zr1?xTix)O3thin films.[16]The large dielectric and piezoelectric properties can be ob-tained at the critical tensile mis fit strain.On the other hand,experimental ferroelectric and piezoelectric properties were measured for epitaxial Pb(Zr1?xTix)O3thin films on different buffer layer/substrates in relation to the mis fit strain.[17]The polarization and dielectric constant were strongly dependent on the mis fit strain.
Therefore,the goal of this work is to investigate the Effect of mis fit strain on the physical properties for(111)oriented Pb(Zr1?xTix)O3thin films.The ferroelectric,dielectric and pyroelectric properties are evaluated as a function of mis fit strain with the different applied electric field.The large dielectric and pyroelectric properties can be achieved at the critical mis fit strain,which may provide guidance for experimental researches.
2 Model and Method
As shown in Ref.[18],the standard Gibbs energy functionG,which is employed in the Landau–Dovenshire theory of bulk ferroelectric crystals,is given by
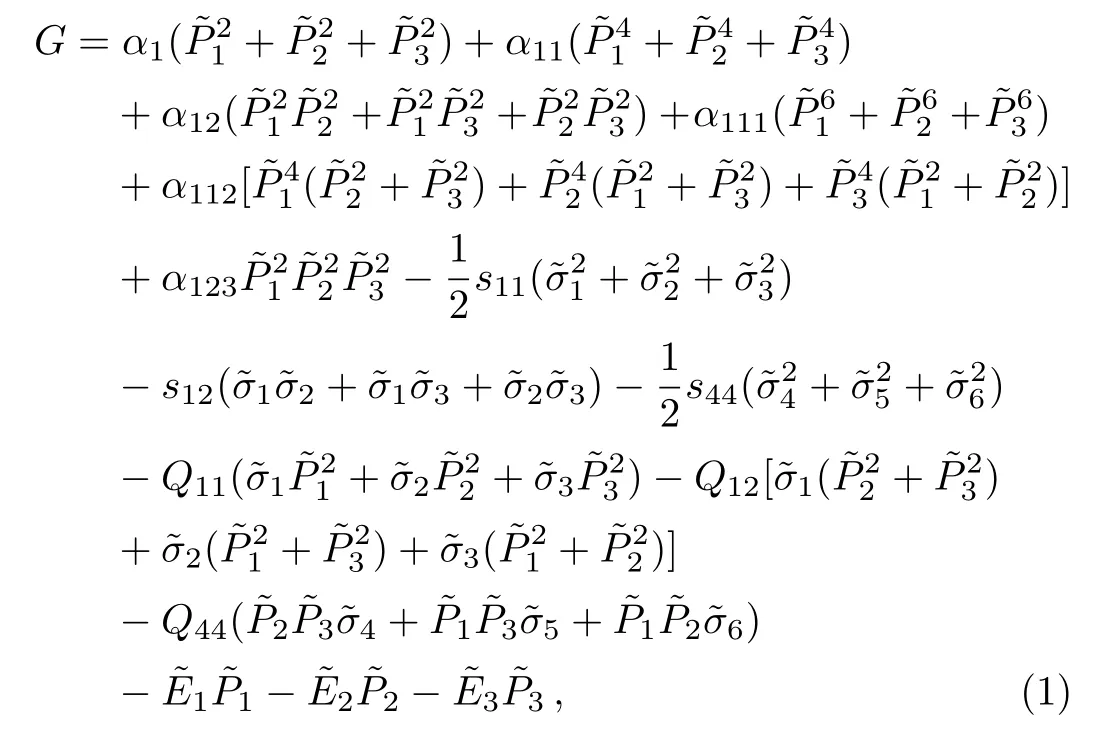
For a(111)oriented thin film,theX3axis is parallel to[111]and perpendicular to the film substrate interface,theX1axis is along the[1ˉ10].Therefore,the frame transformation matrixAi,jis shown below.[20?21]

For a single domain ferroelectric thin film,the thermodynamic potential is obtained by the following Legendre transformation ofG.[18]

whereS1,S2,andS6are the mis fit strains in the Voigt matrix notation.In this paper,we consider the case of a(111)oriented ferroelectric thin film epitaxially grown on a thick substrate.The in-plane mis fit strains are given byS1=S2=Sm,andS6=0.The stressσi(i=1–6)in Eq.(3)can be eliminated by the mechanical boundary conditions:andConsequently,the thermodynamic potential of(111)oriented ferroelectric thin film can be presented as follows.

whereandβijklare the renormalized coefficients and calculated by the dielectric sti ffness coefficientsα1,αij,andαijk,elastic compliancessij,and electrostrictive coefficientsQij.The temperature dependence of ferroelectricity is mainly governed by the renormalized coefficient,and the mis fit strain dependence of ferroelectricity is determined by the coefficientsandβi.All the other renormalized coefficients are taken as temperature and mis fit strain independent parameters.
The polarization componentsPias a function of misfit strain,temperature,and electric field are given by the equilibrium conditionsThe dielectric constantsεijcan be calculated from the reciprocal dielectric susceptibilitieswhich are obtained by differentiating the thermodynamic potentialGfilm.The matrix inversion then enables us to find the dielectric susceptibilityη=χ?1and to compute the dielectric constantBy substituting the polarization componentsPiinto the expression ofχij,the dielectric constantsεijare calculated as a function of misfit strain,temperature,and electric field.
In the presence of an applied electric fieldE3normal to the film substrate interface,the pyroelectric coefficientp3is given as the sum of the variations of the out-ofplane polarization and the dielectric constantε33with the temperature.[22]
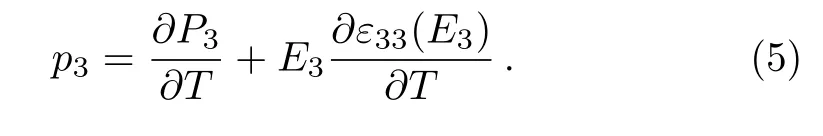
3 Results and Discussion
Based on the “mis fitstrain-temperature” phase diagrams,[23]we introduce the following notations for different equilibrium states that occur at room temperature in(111)oriented Pb(Zr1?xTix)O3thin films:(i)The monoclinicMAphase,whereP1=P2<0,P3>0;(ii)The triclinicγ2phase,whereP1>0,P2>0,P3>0;(iii)The triclinicγ3phase,whereP1<0,P2<0,P3>0,(iv)the triclinicγ4phase,where(v)the triclinicγ5phase,whereThe polarization componentsPiwith the Effect of electric field are presented as a function of mis fit strain in Fig.1.Due to the electric field applied along the[111]and normal to the film substrate interface,the increase of electric field enhances the polarization componentP3.For Pb(Zr0.6Ti0.4)O3thin films,the applied electric field increases the critical mis fit strain corresponding to the phase transition betweenγ4phase andMA(orγ3)phase,and results in the decrease of in-plane polarization componentsP1andP2except the polarization componentP2inγ4phase.As shown in Fig.1(b),the critical mis fit strain betweenγ3phase andMA(orγ2)phase decreases with the applied electric field.WhenE3=200 KV/cm,the triclinicγ2phase transforms to the triclinicγ4phase accompanying the rotation of polarization vectorP.Similarly,the electric field reduces the in-plane polarization componentsP1andP2but the polarization componentP1in the triclinicγ3phase.The triclinicγ5phase of Pb(Zr0.4Ti0.6)O3thin films exists in a narrow region of mis fit strain and disappears as applying an electric field.Moreover,the electric field decreases the critical mis fit strain between theMAphase andγ4phase,and has an opposite Effect on the critical strain between theγ4phase andγ3phase.Undoubtedly,the polarization componentsP1andP2decrease with the increase of electric field except the polarization componentP2in theγ4phase.For Pb(Zr0.3Ti0.7)O3thin films,the electric field has almost no Effect on the critical mis fit strain and in-plane polarization components.

Fig.1 The effects of mis fit strain and electric field on the polarization components Piin(111)oriented Pb(Zr1?xTix)O3(x=0.4,0.5,0.6,0.7)thin films.
The most important dielectric property of a ferroelectric thin film is the out-of-plane permittivityε33,which is measured in a conventional plate-capacitor setup,where the applied electric fieldEis perpendicular to the film surface.The dependence of relative dielectric constantε33/ε0on the mis fit strain is calculated numerically and shown in Fig.2.The applied electric field decreases the relative dielectric constantε33/ε0except in the case of the triclinicγ2phase in Pb(Zr0.5Ti0.5)O3thin films atE3=50 KV/cm,which is in agreement with the experimental measurements.[12]It can be explained that the relative dielectric constantε33/ε0mainly depends on the polarization componentP3.The applied electric field increases the polarization componentP3and thus reduces the relative dielectric constant.AtE3=50 KV/cm in Pb(Zr0.5Ti0.5)O3thin films,the relative dielectric constantε33/ε0ofγ2phase is related with the polarization componentsP1andP3which show different behaviours with the change of mis fit strain.The competition betweenP1andP3gives rise to the dielectric anomaly ofε33/ε0.The mis fit strain corresponding to the maximum ofε33/ε0is about 6×10?3,which corresponds to the inflection point of polarization componentP3.Our calculations indicate that Pb(Zr0.5Ti0.5)O3thin films with the Ti composition around the MPB have the large dielectric property and the Pb(Zr1?xTix)O3thin films with rich Ti(or Zr)composition have the small values,which are in accordance with the other theoretical results.[13]Furthermore,Pb(Zr1?xTix)O3thin films under the monoclinicMAphase have the smaller dielectric property than that of triclinicγphase.That is because the compressive mis fit strain induces the monoclinicMAphase and improves the polarization componentP3,which decreases the relative dielectric constant.

Fig.2 The dependence of relative dielectric constant ε33/ε0on the mis fit strain and electric field in(111)oriented Pb(Zr1?xTix)O3(x=0.4,0.5,0.6,0.7)thin films.
The effects of mis fit strain and electric field on the pyroelectric coefficientp3are exhibited in Fig.3 for(111)oriented Pb(Zr1?xTix)O3thin films.The applied electric field decreases the pyroelectric coefficient,which is in agreement with the theoretical results.[24]Under the effect of electric field,Pb(Zr0.5Ti0.5)O3thin films have the largest pyroelectric coefficient because of the Ti composition near the MPB,which agrees well with the experimental observations.[10]The pyroelectric coefficientp3atE3=10 KV/cm is 8×10?4C/m2K(not shown here)which is comparable with the result of(001)oriented Pb(Zr0.5Ti0.5)O3thin films.[25]As the electric field increases to 0 KV/cm,the large pyroelectric coefficient of 2×10?3C/m2K can be obtained at the critical mis fit strain of 6×10?3,which is similar to the behavior of relative dielectric constant.Experimentally,the pyroelectric coefficient of 3×10?4C/m2K was observed in highly(111)oriented Pb(Zr0.3Ti0.7)O3thin films which is coincident with our theoretical result.[26]Therefore,it is concluded that the pyroelectric Effect largely depends on the mis fit strain.Control of the mis fit strain is an effective method to improve the physical properties which may open more opportunities for practical applications.

Fig.3 The pyroelectric coefficient p3of(111)oriented Pb(Zr1?xTix)O3(x=0.4,0.5,0.6,0.7)thin films as a function of mis fit strain.
4 Conclusion
In summary,the Effect of mis fit strain on the dielectric and pyroelectric properties is investigated for(111)oriented Pb(Zr1?xTix)O3thin films by using the Landau–Dovenshire theory.The dielectric and pyroelectric properties are largely dependent on the mis fit strain and large values of these properties are obtained in Pb(Zr0.5Ti0.5)O3thin films at the critical mis fit strain.The Effect of electric field on the dielectric and pyroelectric properties is evaluated and the calculations are in agreement with the experimental measurements.The pyroelectric coefficient of 2×10?3C/m2K obtained in Pb(Zr0.5Ti0.5)O3thin films is much larger than that of(001)oriented films,which may provide a guide for experimental work.
References
[1]J.F.Scott and C.A.Paz de Araujo,Science246(1989)1400.
[2]F.Akasheh,T.Myers,J.D.Fraser,S.Bose,and A.Bandyopadhyay,Sensor.Actuat.A-Phys.111(2004)275.
[3]M.Kohli,C.Wuethrich,K.Brooks,B.Willing,M.Forster,P.Muralt,N.Setter,and P.Ryser,Sens.Actuators,A60(1997)147.
[4]D.M.Kim,C.B.Eom,V.Nagarajan,J.Ouyang,R.Ramesh,V.Vaithyanathan,and D.G.Schlom,Appl.Phys.Lett.88(2006)142904.
[5]Y.Shi,M.Cue ff,G.Niu,et al.,J.Appl.Phys.115(2014)214108.
[6]J.Yu,X.J.Meng,J.L.Sun,Z.M.Huang,and J.H.Chu,J.Appl.Phys.96(2004)2792.
[7]K.Nagashima,M.Aratani,and H.Funakubo,J.Appl.Phys.89(2001)4517.
[8]S.Utsugi,T.Fujisawa,Y.Ehara,T.Yamada,M.Matsushima,H.Morioka,and H.Funakubo,Appl.Phys.Lett.96(2010)102905.
[9]Z.X.Zhu,J.F.Li,F.P.Lai,et al.,Appl.Phys.Lett.91(2007)222910.
[10]D.Akai,M.Yokawa,K.Hirabayashi,K.Matsushita,K.Sawada,and M.Ishida,Appl.Phys.Lett.86(2005)202906.
[11]S.Yokoyama,Y.Honda,H.Morioka,et al.,J.Appl.Phys.98(2005)094106.
[12]T.Oikawa,M.Aratani,H.Funakubo,K.Saito,and M.Mizuhira,J.Appl.Phys.95(2004)3111.
[13]X.H.Du,J.H.Zheng,U.Belegundu,and K.Uchino,Appl.Phys.Lett.72(1998)2421.
[14]L.Lian and N.R.Sottos,J.Appl.Phys.87(2000)3941.
[15]J.P′erez de la Cruz,E.Joanni,P.M.Vilarinho,and A.L.Kholkin,J.Appl.Phys.108(2010)114106.
[16]N.A.Pertsev,V.G.Kukhar,H.Kohlstedt,and R.Waser,Phys.Rev.B67(2003)054107.
[17]M.D.Nguyen,M.Dekkers,E.Houwman,et al.,Appl.Phys.Lett.99(2011)252904.
[18]N.A.Pertsev,A.G.Zembilgotov,and A.K.Tagantsev,Phys.Rev.Lett.80(1998)1988.
[19]M.J.Haun,Z.Q.Zhuang,E.Furman,S.J.Jang,and L.E.Cross,Ferroelectrics99(1989)45.
[20]S.Schmidt,J.W.Lu,S.P.Keane,L.D.Bregante,D.O.Klenov,and S.Stemmerw,J.Am.Ceram.Soc.88(2005)789.
[21]A.K.Tagantsev,N.A.Pertsev,P.Muralt,and N.Setter,Phys.Rev.B65(2001)012104.
[22]H.X.Cao,V.C.Lo,and Z.Y.Li,J.Appl.Phys.101(2007)014113.
[23]J.H.Qiu,Z.H.Chen,X.Q.Wang,N.Y.Yuan,and J.N.Ding,Solid State Commun.246(2016)5.
[24]M.T.Kesim,J.Zhang,S.Trolier-McKinstry,J.V.Mantese,R.W.Whatmore,and S.P.Alpay,J.Appl.Phys.114(2013)204101.
[25]A.Sharma,Z.G.Ban,S.P.Alpay,and J.V.Mantese,J.Appl.Phys.95(2004)3618.
[26]N.M.Shorrocks,A.Patel,M.J.Walker,and A.D.Parsons,Microelectron.Eng.29(1995)59.
 Communications in Theoretical Physics2016年10期
Communications in Theoretical Physics2016年10期
- Communications in Theoretical Physics的其它文章
- Relativistic Correction on Neutrino Emission from Neutron Stars in Various Parameter Sets?
- Study of Friction between Liquid Crystals and Crystalline Surfaces by Molecular Dynamic Simulations?
- A Complex Network Model for Analyzing Railway Accidents Based on the Maximal Information Coefficient?
- First-Principles Study of Structural,Magnetic,Electronic and Elastic Properties of PuC2?
- Critical Behavior of Spatial Evolutionary Game with Altruistic to Spiteful Preferences on Two-Dimensional Lattices?
- In fluence of Defects and Crystallographic Orientation on Mechanical Behavior of Nanocrystalline Aluminium?
