Advanced multiple response surface method of sensitivity analysis for turbine blisk reliability with multi-physics coupling
Zhng Chunyi,Song Luki,b,Fei Chengwei,Lu Cheng,Xie Yongmei
aSchool of Mechanical and Power Engineering,Harbin University of Science and Technology,Harbin 150080,China
bSchool of Energy and Power Engineering,Beihang University,Beijing 100083,China
cDepartment of Mechanical Engineering,The Hong Kong Polytechnic University,Kowloon 999077,China
Advanced multiple response surface method of sensitivity analysis for turbine blisk reliability with multi-physics coupling
Zhang Chunyia,Song Lukaia,b,Fei Chengweib,c,*,Lu Chenga,Xie Yongmeia
aSchool of Mechanical and Power Engineering,Harbin University of Science and Technology,Harbin 150080,China
bSchool of Energy and Power Engineering,Beihang University,Beijing 100083,China
cDepartment of Mechanical Engineering,The Hong Kong Polytechnic University,Kowloon 999077,China
To reasonably implement the reliability analysis and describe the significance of influencing parameters for the multi-failure modes of turbine blisk,advanced multiple response surface method(AMRSM)was proposed for multi-failure mode sensitivity analysis for reliability.The mathematical model of AMRSM was established and the basic principle of multi-failure mode sensitivity analysis for reliability with AMRSM was given.The important parameters of turbine blisk failures are obtained by the multi-failure mode sensitivity analysis of turbine blisk.Through the reliability sensitivity analyses of multiplefailure modes(de formation,stress and strain)with the proposed method considering fluid–thermal–solid interaction,it is shown that the comprehensive reliability of turbine blisk is 0.9931 when the allowable deformation,stress and strain are 3.7×10-3m,1.0023×109Pa and 1.05×10-2m/m,respectively;the main impact factors of turbine blisk failure are gas velocity,gas temperature and rotational speed.As demonstrated in the comparison of methods(Monte Carlo(MC)method,traditional response surface method(RSM),multiple response surface method(MRSM)and AMRSM),the proposed AMRSM improves computational efficiency with acceptable computational accuracy.The efforts of this study provide the AMRSM with high precision and efficiency for multi-failure mode reliability analysis,and of fer a useful insight for the reliability optimization design of multi-failure mode structure.
1.Introduction
As the heart of aircraft,aeroengine directly influences the safety and reliability of flight.1Turbine blisk,as one of the core components of aeroengine,effects the reliable and stable operation of aeroengine.However,turbine blisk always bears many loads from high temperature,high pressure and high rotational velocity,and holds many failure modes in operating process,such as strain failure,de formation failure,and so forth.2There fore,it is significant to carry out reasonable and effective reliability analysis.
Plentiful studies on structure reliability analysis lead to the development of reliability analysis methods.3For instance,Kaymaz4studied the structural reliability problem based on Kriging model;Lin et al.5discussed the reliability of coupled oscillators;Dimitrov et al.6proposed the model factor rectification method for the reliability analysis of composite turbine blade based on finite element technology.Hu et al.7completed the reliability analysis of turbine blade by the stochastic chaos polynomial expansion method approximating to structural limit-statefunction considering fluid dynamics.In order to solve the multi-source uncertainty problem of structure reliability analysis,Wang et al.8discussed the hybrid reliability analysis method based on the convex model theory and compared with the conventional probabilistic analysis method.
As an important approach,response surface method(RSM)is widely used in structural reliability analysis.9–11Zhang and Bai GC9developed extremum response surface method for the reliability analysis of two-link flexible robot manipulator;Krishnamurthy10compared the response surface construction methods for derivative estimation using moving least squares,Kriging and radial basis functions;Xiong et al.11advanced a double weighted stochastic response surface method for reliability analysis.To further improve the computational efficiency and precision,many works have been done.Fei and Bai GC12,13adopted support vector machine response surface method for structural reliability analysis.Ren and Bai GC14established artificial neural network(ANN)response surface model by integrating ANN algorithm with high accuracy and nonlinear mapping ability;Lv et al.15proposed the weight line response surface method based ANN for reliability analysis.To analyze the effect of high temperature heat translation on the reliability analysis of blisk structure,Bai B and Bai GC16completed the sensitivity analysis for blisk reliability by proposing extremum response surface method.
However,those methods are only fitted for structure reliability analysis with singlefailure mode.Few efforts on the multi-discipline and multi-object reliability analysis are done besides Fei et al.17–19Fei and Bai GC17proposed distributed collaborative extremum response surface method for the transient design of mechanical dynamic assembly reliability;Bai GC and Fei18proposed distributed collaborative response surface method for the design of mechanical dynamic assembly reliability;Zhai et al.19completed sensitivity analysis for the reliability of high pressure turbine blade-tip radical running clearance by adopting multiple response surface method.However,those achievements are only considered with onefailure mode rather than multiplefailure modes for the reliability analysis of complex structure.
The objective of this paper is to propose an advanced multiple response surface method(AMRSM)based on intelligent algorithm with high nonlinear mapping ability and response surface method for structural reliability analysis.The AMRSM mathematical model is established by integrating particleswarm optimization(PSO),ANN andmultiple response surface theory.The reliability analysis of an aeroengine turbine blisk is implemented by reasonably selecting random variables and taking the de formation,stress and strain of turbine blisk as output response.Through the comparison of methods(Monte Carlo(MC)method,traditional response surface method(RSM),multiple response surface method(MRSM)and AMRSM),19the effectiveness and reasonability of the presented AMRSM are validated.
In what follows,in Section 2,AMRSM is studied including the basic idea and mathematical model of AMRSM and intelligent operator.Section 3 focuses on reliability sensitivity approach.The sensitivity analysis for turbine blisk reliability is achieved in Section 4.Section 5 summarizes the conclusions of this study.
2.AMRSM
2.1.MRSM
The basic thought of MRSM is shown as follows:
(1)The single response surface model between input random variables xiand output response y(xi)is established for each failure mode of structure.
(2)Multiple response surface models are established based on single response surface model for structure reliability analysis rather than finite element method(FEM).
In line with the basic thought of MRSM,the stochastic problem of nonlinear complex structure reliability analysis is trans formed into the problem of solving mathematical model,which greatly reduces computational time and improves computational efficiency.19The mathematical model of MERM is shown as:
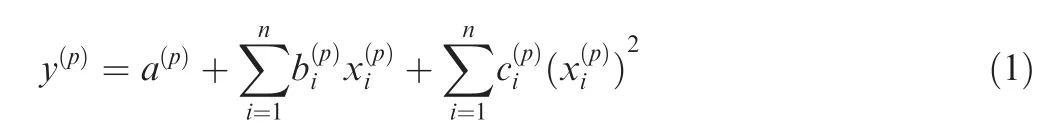
where y(p)is the pth output response;the ith component of the variable x corresponding to the pth output response;the constant item;the coefficients of linear polynomial;the coefficients of quadratic polynomial;n is the number of variables in x.
2.2.AMRSM of structure reliability analysis
2.2.1.Basic thought of AMRSM
Reliability analysis is to adopt the random dispersion of random variables to analyze the probability that the structure meet the specified function in the practical engineering.In order to realize the comprehensive reliability analysis of multi-failure mode structure by using traditionalRSM,AMRSM was advanced for structure reliability analysis on the foundation of MRSM.The basic thought is that(1)the random input variables are determined and the finite element(FE)model of structure is established;(2)according to the FE model,a number of samples are extracted as training sam-ples;(3)the number of nodes in each layer of neural network is defined,and many neural network models arefitted to these training samples;(4)the initial optimal weights and threshold of each neural network model are searched by using PSO;(5)the multiple response surface models with neural network are built by Bayesian regularization algorithm(BRA).The output response values are obtained by MC method linkage sampling of advanced multiple response surface models.The reliability analysis procedure of turbine blisk with AMRSM is shown in Fig.1.
2.2.2.Mathematical model of AMRSM
Arbitrary shape and strong adaptivity are the features of neural network,which may accurately fit the complex function relationship between random variables and response variable.back-propagation artificial neural network(BP-ANN)topology model is shown in Fig.2.The function relationship between response y and input variables x can be structured as
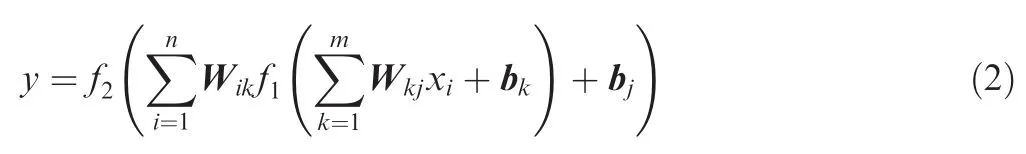
where Wikis the connection weight between the ith node of input layer and the kth node of hidden layer;bkis the kth threshold value of hidden layer;Wkjis the connection weight between the kth node of hidden layer and the jth node of output layer;bjis the jth threshold value of the output layer;f1(·)and f2(·)are the transfer functions of hidden layer and output layer,respectively;m and n are the number of nodes in input layer and hidden layer,respectively.
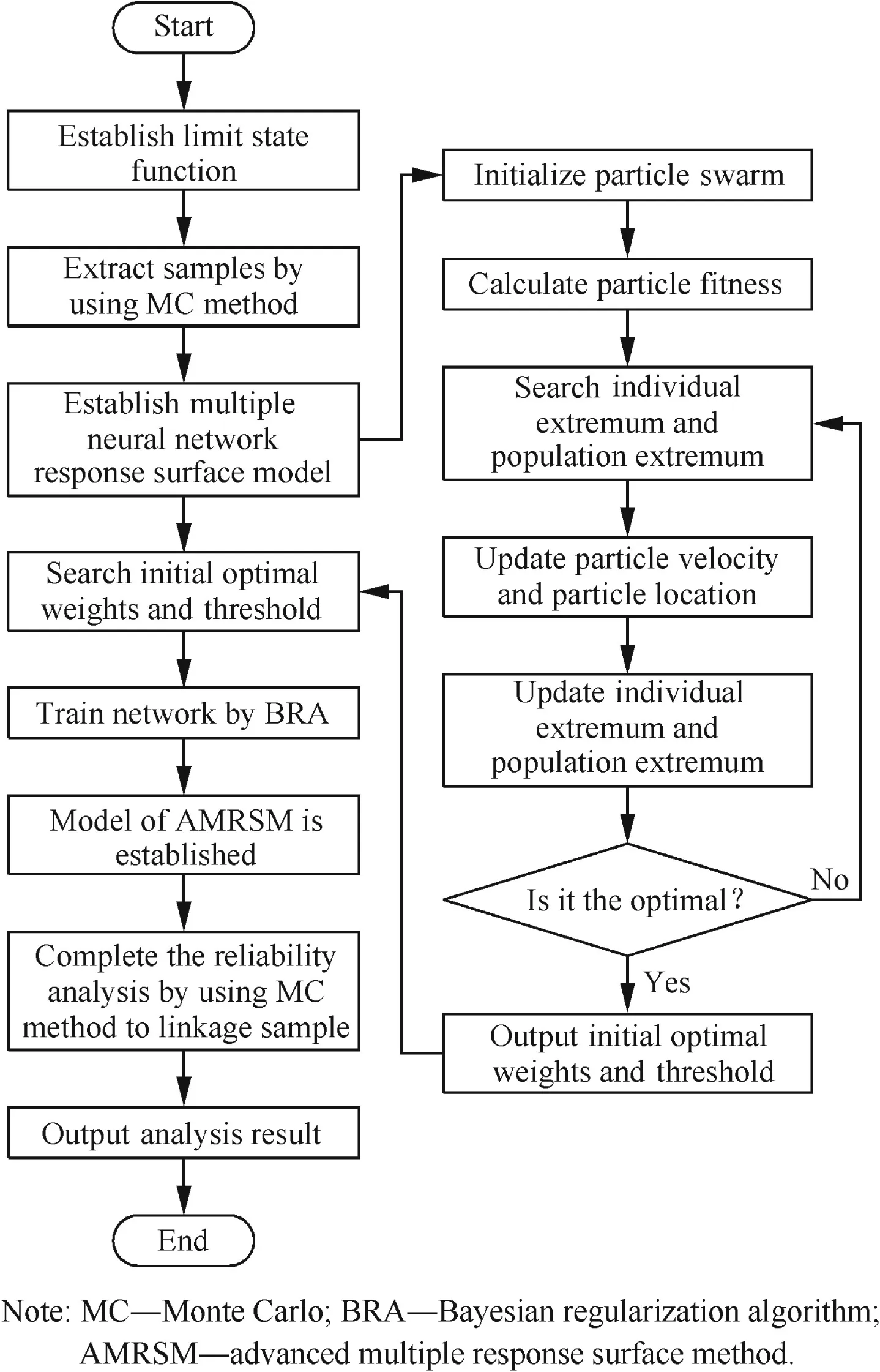
Fig.1 Reliability analysis procedure of turbine blisk with AMRSM.
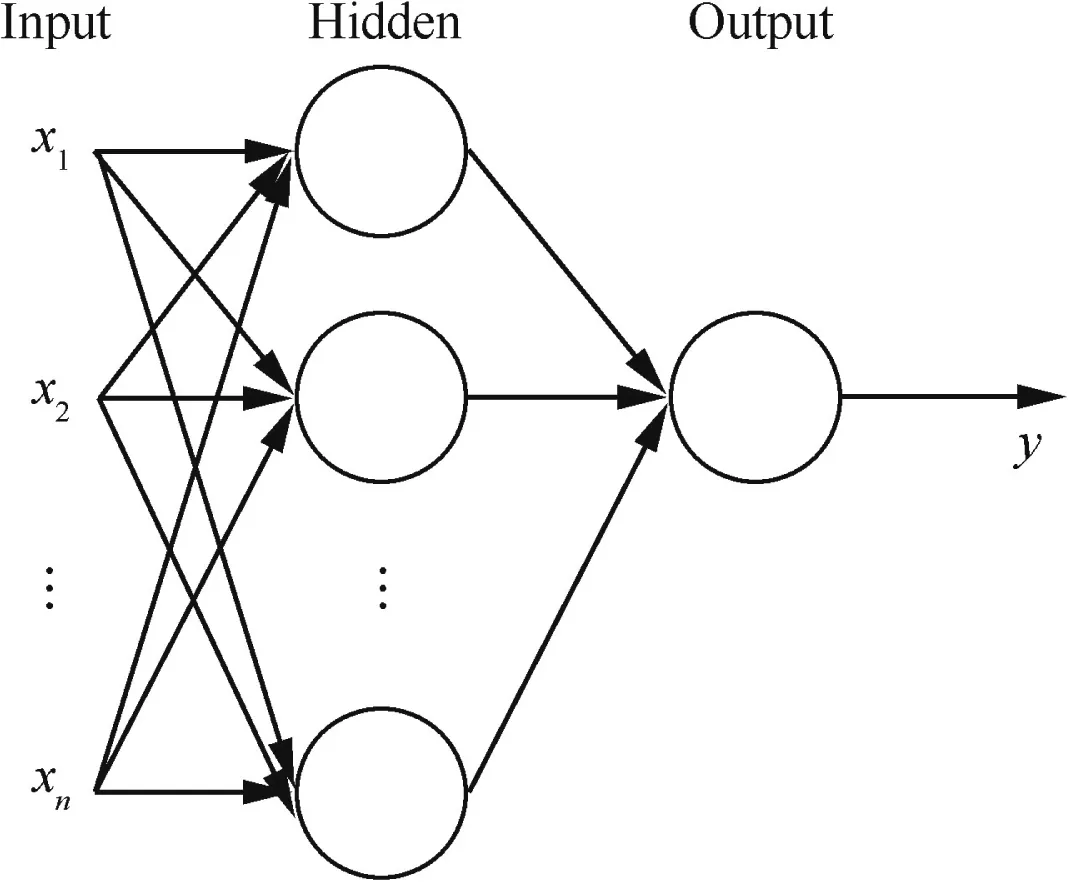
Fig.2 Back-propagation artificial neural network(BP-ANN)topology model.
Through the establishment of many response surface models for each failure mode,the advanced multi-response surface model is shaped as
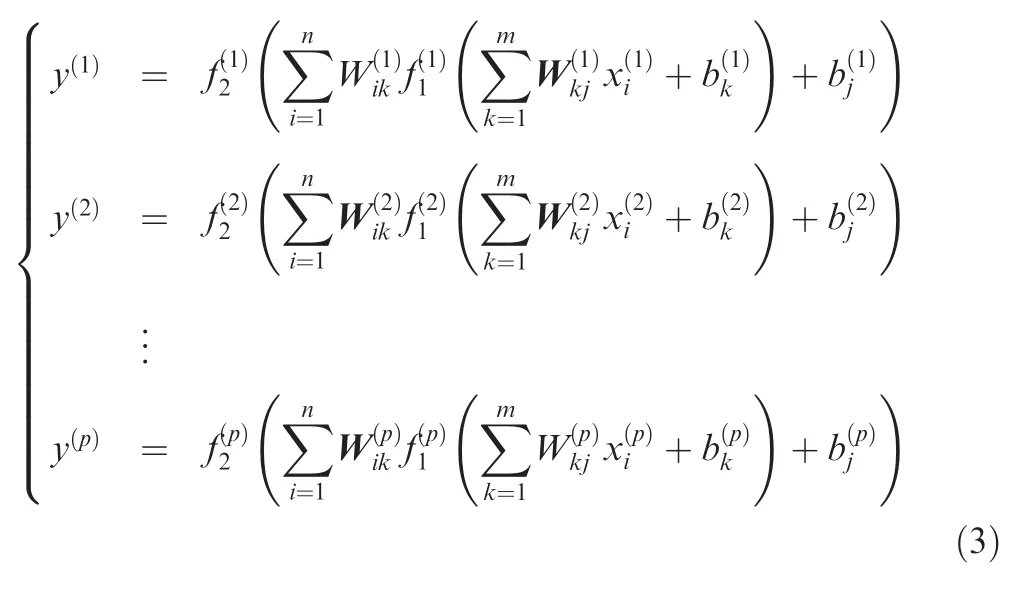
2.2.3.Intelligent operators
As a kind of emerging algorithm,intelligent algorithm is now widely employed in many fields of parallel search and pattern recognition,which is promising for addressing the complex computation problem by simulating biological evolution.Particle swarm operator is prone to premature convergence or local optimal problem during intelligent search,which seriously impacts the accuracy of network model.The training operator of general BP network has slow convergence speed,low approximation accuracy and weak generalization ability,so that the accuracy of complex structure reliability analysis is always unacceptable.Accordingly,it is significant for the improvement of the precision of reliability analysis to effectively design particle swarm operator and training operator.Currently,the PSO has been widely applied to function optimization,neural network training and fuzzy system control due to easy realization and high searching efficiency.20
Firstly,the number of particles is determined and each particle is initialized in space.Hereinto,each particle has a potential solution.All particles search for the optimal solution in the solution space by following current optimal particles and tracking individual extreme values and population extremum to update individual position to research for the optimal solution.The renewal particle position and velocity are where w is the inertia weight;d is the search space dimension;i is the ith particle;k is the current iteration number;Vidis the current particle velocity;Pidis the current individual extremum;Pgdis the current population extremum;c1and c2are the non-negative acceleration factors;r1and r2are the random numbers during time domain[0,1].
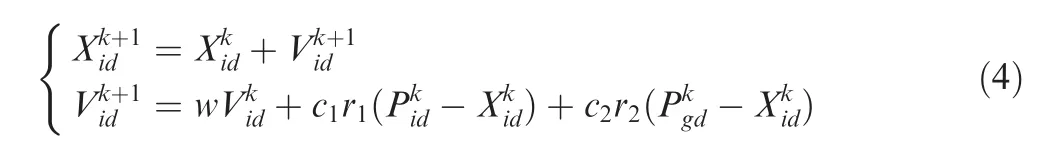
Inertia weight w reflects the degree of the current velocity inheriting the previous velocity. Larger inertiaweight is beneficial to global search,while small inertia weightmakes for local search.To better balance the global and local search ability,this paper adopts the adaptive inertia weight changing with iterations,i.e.,

where w1is the initial inertia weight;w2the inertia weight at the largest number of iteration;t the current iteration number;T the largest iteration number.
Gradient decent method is general BP network training algorithm,which does not have a good application in complex nonlinear function approximation due to low approximation accuracy and weak generalization ability.For the problem of the algorithm,BRA is chosen to train ANN model in this paper.The algorithm is able to effectively improve the generalization of ANN through solving the over-fitting problem by continuously reducing the weights and threshold values in training process.Its performance function is

where
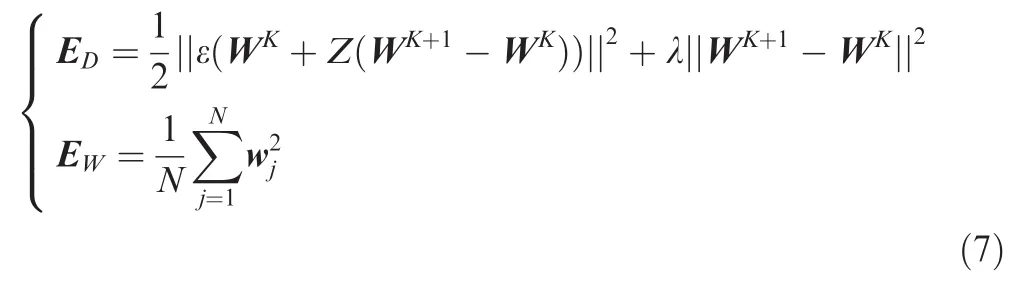
where k1and k2are the proportional coefficients;wjis the weight of ANN;ε is the expected error function of output response;W is the vector of weight and threshold value for network layers;K is the iteration number;Z is the Jacobian matrix of ε;λ is the iteration variable.
3.Reliability sensitivity
The reliability sensitivity reflects the influence level of the variation of random variables on failure probability.By MC simulation,the failure probability is achieved as

where μgand Dgare the mean and variance matrixes of the limit statefunction,respectively; Φ(·)is the standard normal distribution function.
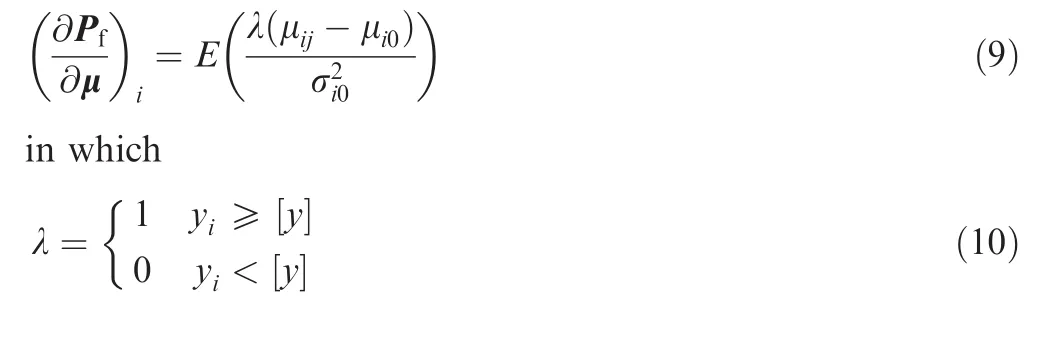
The sensitivity of the mean matrix of random variables is represented by in which E(·)is thefunction of mean values;μijthe jth datum in the ith input variable;μi0the mean value of the ith input variable;σi0the variance of the ith input variable;yjthe jth output response;[y]the allowable de formation.
4.Example analysis
Gas turbine engine works in harsh environment so that the turbine blisk endures high temperature and high rotation speed.There fore,it is difficult to get a coupled solution of the basic variables in fluid flow,heat transfer and structural response system simultaneously.In order to simplify the calculation under real working conditions,the relaxation coupling method was adopted to carry out the deterministic analysis of blisk considering fluid–thermal–structure interaction.
4.1.Fluid–thermal–structure interaction analysis of turbine blisk

Fig.3 Structure model of blisk.
Fig.4 Flow field grid of blisk.
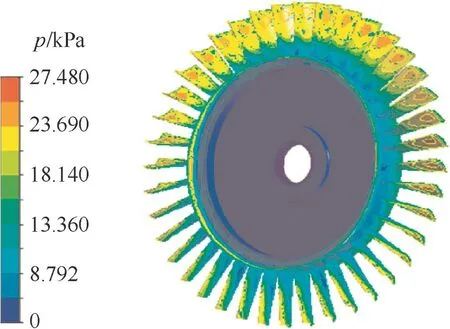
Fig.5 Static pressure distribution of blisk surface.

Fig.6 Blisk grid.
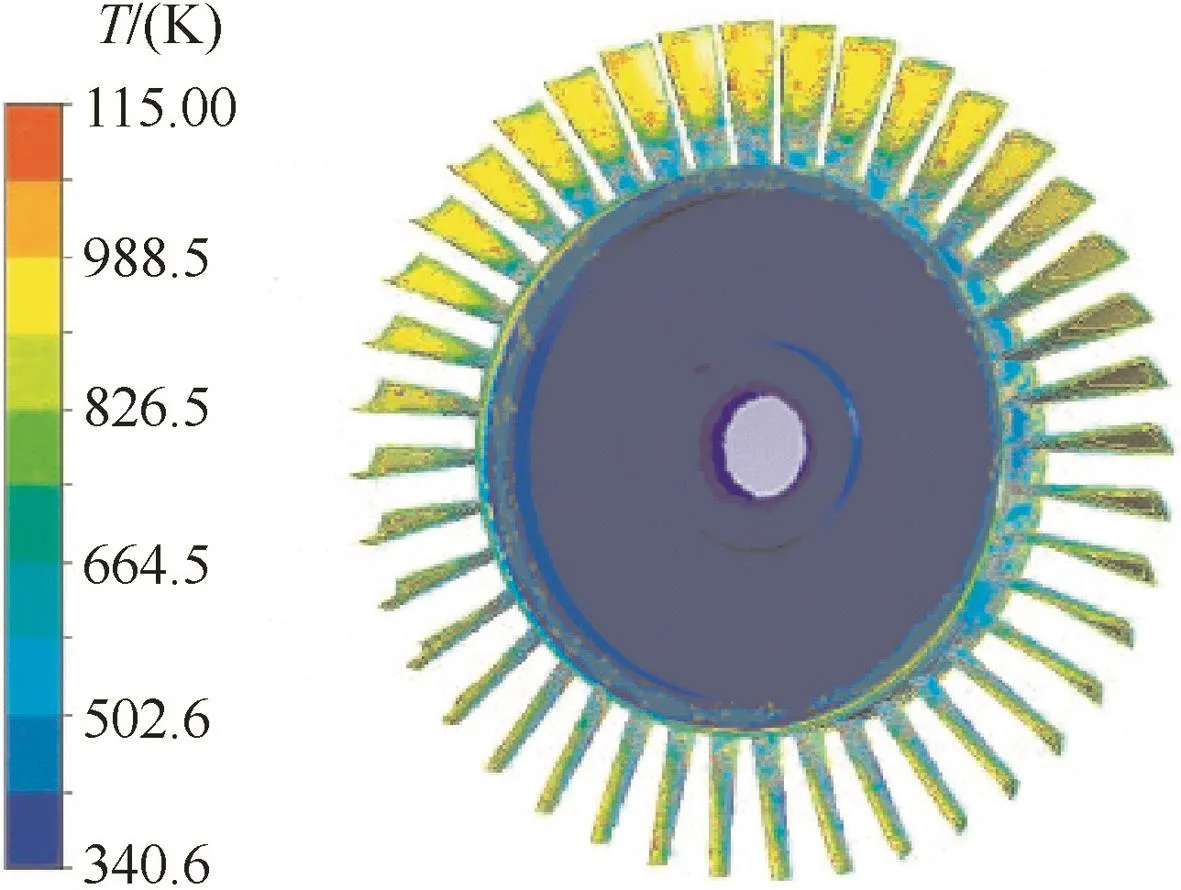
Fig.7 Temperature distribution of blisk surface.
Turbine blisk of aeroengine was taken as the object of study(Fig.3)to validate the proposed methods.The deterministic analysis of turbine blisk was completed under the consideration of fluid–thermal–structure interaction.The diameter of blisk is 0.75 m and the material is TC4 alloy.21It is assumed that inlet fluid velocity,inlet pressure,gas temperature and rotational speed are 160 m/s,600 kPa,1150 K and 1168 rad/s,respectively.
4.1.1.Fluid analysis of blisk
In fluid analysis,the cylinder region with the length 1.2 m and the diameter 2 m was established for the fluid field of blisk model.The fluid field zone was meshed in Fig.4,in which the element number is 598428,and the node number is 842703.The simulation analysis of turbine blisk fluid field was executed by finite element volume method and standard k–ε turbulence model.22The static pressure distribution of blisk surface is shown in Fig.5.
4.1.2.Thermal analysis on blisk
High temperature gas flow from combustion chamber imposes on the surface of blisk and thus makes blisk surface temperature rise by heat transfer and heat convection.The grid of blisk is shown in Fig.6 where the number of element is 34875,and the number of node is 68678.The distribution of blisk surface temperature is shown in Fig.7.
4.1.3.Structure analysis of blisk
In the analysis of blisk,the blisk material parameters and rotational speed were determined firstly.And then the fluid pressure and temperature load were loaded into the fluid–solid interface of blisk.Finally,the analyses of de formation,stress and strain were completed under the effect of fluid pressure,thermal stress and centrifugal force.The distributions of de formation,stress and strain are shown in Fig.8.As illustrated in Fig.8,the maximum de formation of blisk locates on blade-tip,while the maximum stress and strain of blisk are on the root of disk.
4.2.Sensitivity analysis for blisk reliability
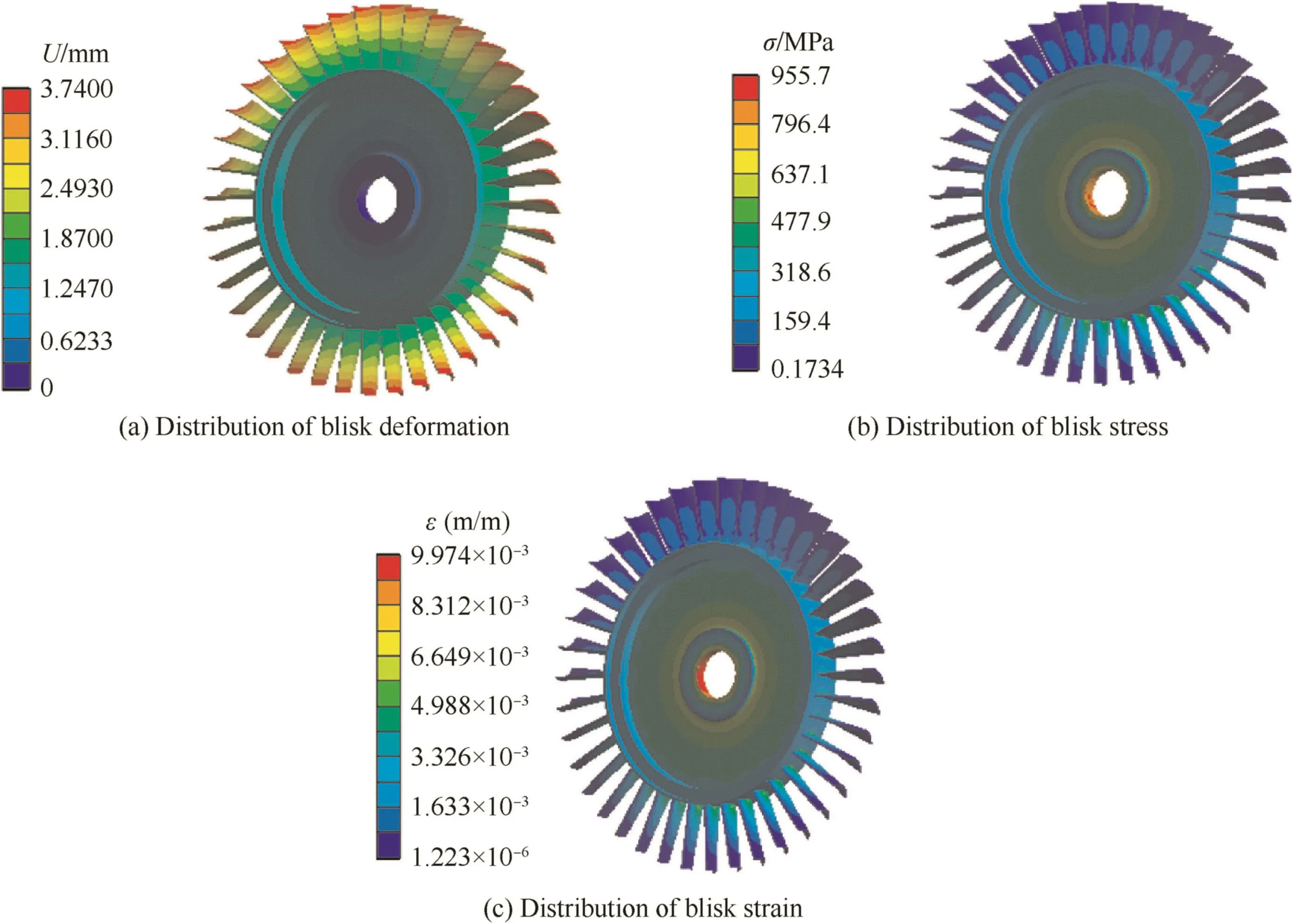
Fig.8 Distributions of blisk deformation,stress and strain.
In the light of the uncertainties of material parameters mentioned in the handbook21and working condition of blisk from aeroengine tests,the inlet velocity v,inlet pressure p,temperature T,material density ρ and rotational speed ω were reasonably chosen as input random variables,which were assumed to follow normal distribution and be independent mutually.The distributions of input random variables are listed in Table 1.
The input random variables were sampled by the composite sampling technique at the location of maximum de formation,stress and strain of turbine blisk.The output response values of maximum deformation,stress and strain were obtained by the fluid–thermal–solid coupling analysis based on these samples.The normalized data were taken as the training samples of ANN.And the 5-3-1 three-layer network structure was chosen as the BP-ANN model where the transfer functions from input layer to hidden layer and hidden layer to output layer as well as the training function are ‘tansig’, ‘purelin’and‘trainbr’,respectively,and particle dimension θ =16 and particle number N=40 are selected for the BP-ANN model.Through 100 iterations,the optimal fitness value curves are shown in Fig.9.
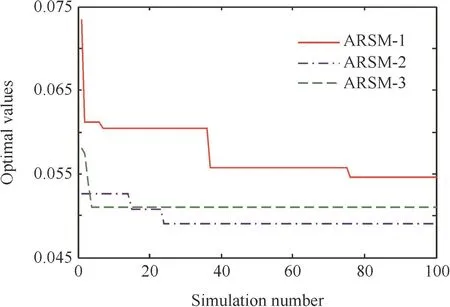
Fig.9 Optimal fitness value curves.
As indicated in Fig.9,the optimal fitness values are steady when the number of simulations reach at 76,22 and 3,respectively, for de formation’s ARSM(ARSM-1),stress’ARSM(ARSM-2)and strain’s ARSM(ARSM-3).In other words,76 iterations are promising to stabilize all the optimal fitness values for three ARSMs.There fore,the samples from 100 iterations completely satisfy the establishment of the advanced response surface model(BP-ANN model).


Table 1 Distributions of input random variables.

Table 2 Results of turbine blisk reliability analysis.
The initial optimal weights and threshold values are inputted into ANN model.Through network training with BRA,the advanced multiple response surface function is obtained where the weight and threshold levels of two members are shown in Eqs.(11)–(13).
Through 10000 simulations on three advanced response surfaces by MC simulation method,the output responses are obtained by inversed normalization.Based on the related parameters in an aeroengine material handbook21and some related material tests,it can befound that the allowable de formation,allowable stress and allowable strain are 3.7×10-3m,1.0023×109Pa and 1.05×10-2m/m,respectively.Referencing these material parameters,the results of turbine blisk reliability analysis are listed in Table 2.In Table 2,thefailure number and the reliability are obtained by comparing the response values calculated by ARSM with the allowable values.Thefailure number is the number of output responses which are greater than the corresponding allowable values,while the reliability is the ratio of the number of response values,less than the corresponding allowable values,to the total response number.The curves and distributions of maximum deformation,stress and strain are shown in Figs.10 and 11.In line with Eqs.(9)and(10),the results of sensitivity analysis for turbine blisk reliability are shown in Fig.12 and Table 3.
4.3.AMRSM verification
To verify the AMRSM,the reliability analyses of turbine blisk were carried out with MC method,RSM,MRSM and AMRSM under the same computational conditions.All analyses are per formed by the automatic parallel operation on three Intel Pentium 4 desktop computers with 2.13 GHz CPU and 4GB RAM.The computational time and reliability with four methods are shown in Tables 4 and 5.

Fig.10 Simulation histories of blisk de formation,stress and stain.
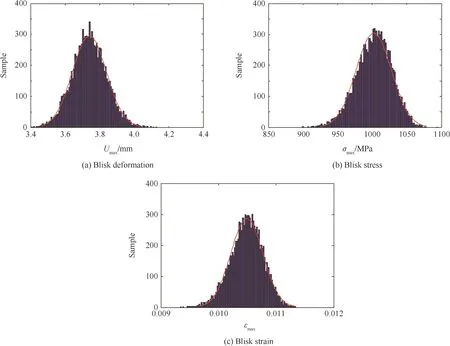
Fig.11 Distributions of blisk output response.
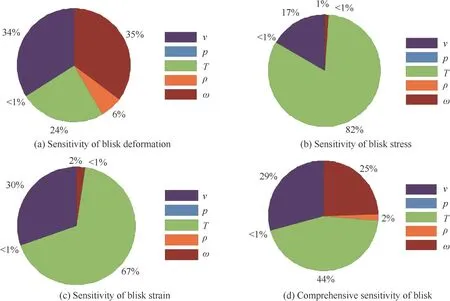
Fig.12 Results of blisk sensitivity analysis.
4.4.Discussion
As demonstrated from Table 2,Figs.10 and 11,the reliability degrees of blisk de formation,stress and strain are 99.45%,99.44%and 99.72%respectively when the designed de formation,stress and strain of blisk are 3.7 m,1.0023×109Pa and 1.05×10-2m/m.Under this condition,the comprehensive reliability degree of turbine blisk is 0.9931.The resultsare promising to satisfy the requirement of engineering design.

Table 3 Sensitivities and impact probabilities of input random variables.

Table 4 Computational time of blisk reliability analyses with four methods.

Table 5 Computing precision of blisk reliability analyses with four methods.
As revealed by Fig.12 and Table 3,the inlet gas velocity,temperature and rotating speed are main factors for the total deformation of blisk with the influence probabilities 34%,24%and 35%,respectively.The effects of the inlet gas velocity and temperature on the stress of blisk are over 98%,in which the influence of gas temperature holds the greatest effect due to its impacting probability over 82%.The main factors of blisk strain are inlet gas velocity and temperature because of their influence probabilities 30%and 67%,respectively.
As shown from the results of comprehensive sensitivity analysis,the main factors of blisk failure are inlet fluid velocity,temperature and rational speed corresponding to the influence probabilities 29%,44%and 25%,respectively.In the effect of the variables on the failure probability,the variable is positively related with the output response as the sensitivity is positive value,while negative sensitivity indicates that the output response negatively changes with the random variable.Comprehensively considering blisk failure,we can see that the reduction of fluid velocity and fluid pressure causes the increase of blisk failure probability,while the increases of temperature,density and rotational speed lead to the increases of blisk failure probability,which is basically consistent with practical engineering.
As revealed in Table 4 and 5,the computing time of RSM,MRSM and AMRSM is far less than that of MC method.With the increase of the simulation times,the computational efficiency of AMRSM is higher than RSM and MRSM.Thus,the presented AMRSM is proved to hold the highest computational efficiency and speed due to the smallest time consumption.In the aspect of calculation accuracy,AMRSM is almost consistent with MC method,and higher than MRSM and RSM.There fore,the AMRSM is demonstrated to be a highly accurate and highly efficient approach for reliability analysis.
5.Conclusions
(1)The reliability probability of blisk deformation,stress and strain are 0.9945,0.9944,0.9972 and 0.9931,respectively,and the comprehensive reliability degree of turbine blisk is 0.9931 when the designed de formation,stress and strain of turbine blisk are 3.7×10-3m,1.0023×109Pa and 1.05×10-2m/m.
(2)The inlet gas velocity,temperature and rotating speed are main factors for the total deformation of blisk.The effect probabilities of the inlet gas velocity and tem-perature on the stress of blisk are about 17%and 82%.The main factors leading to blisk strain are inlet gas velocity and temperature.
(3)As shown from the results of comprehensive sensitivity analysis,the main factors of blisk failure are inlet fluid velocity,temperature and rational speed.Meanwhile,blisk failure is negatively influenced by gas velocity and pressure and positively affected by gas temperature,material density and rotational speed.
(4)AMRSM holds high computational precision and efficiency from the comparison of methods.With the increase of simulation number,the advantages of AMRSM are more obvious.The results demonstrate that AMRSM is a feasible and efficient method for reliability analysis of multiplefailure mode structures.
Acknowledgements
This study was co-supported by the National Natural Science Foundation of China(No.51275138),the Science Foundation of Heilongjiang Provincial Department of Education(No.12531109),the funding of Hong Kong Scholars Programs(Nos.XJ2015002 and G-YZ90)and China’s Postdoctoral Science Funding(No.2015M580037).
1.Sun C,He ZJ,Zhang ZS,Chen XF,Cao HR,Ning XY,et al.Operating reliability assessment for aero-engine based on condition monitoring in formation.J Mech Eng 2013;49(6):30–7[Chinese].
2.Chen YS,Zhang HB.Review and prospect on the research of dynamics of complete aero-engine system.Acta Aeronaut Astronaut Sin 2011;32(8):1371–9[Chinese].
3.Gokhale SS,Lyu MR.A simulation approach to structure based sof tware reliability analysis.IEEE Trans Sof tware Eng 2005;31(8):643–56.
4.Kaymaz I.Application of Kriging method to structural reliability problems.Struct Saf 2005;27(2):133–51.
5.Lin KK,Shea-Brown E,Young LS.Reliability of coupled oscillators.J Nonlinear Sci 2009;19(5):497–545.
6.Dimitrov N,Friis-Hansen P,Berggreen C.Reliability analysis of a composite wind turbine blade section using the model correction factor method:Numerical study and validation.Appl Compos Mater 2013;20(1):17–39.
7.Hu Z,Li HF,Du XP,Chandrshekhara K.Simulation-based timedependent reliability analysis for composite hydrokinetic turbine blades.Struct Multidiscip Optim 2013;47(5):765–81.
8.Wang L,Wang X,Xia Y.Hybrid reliability analysis of structures with multi-source uncertainties.Acta Mech 2014;225(2):413–30.
9.Zhang CY,Bai GC.Extremum response surface method of reliability analysis on two-link flexible robot manipulator.J Cent South Univ 2012;19(1):101–7.
10.Krishnamurthy T.Comparison of response surface construction methods for derivative estimation using moving least squares,Kriging and radical basis functions.Proceedings of 46th AIAA/ASME/ASCE/AHS/ASC structures,structuraldynamics,and materials conference;2005 April 18–20;Austin 485(TX).Reston:AIAA;2005.p.182–7.
11.Xiong FF,Liu Y,Xiong Y,Yang SX.A double weighted stochastic response surface method for reliability analysis.J Mech Sci Technol 2012;26(8):2573–80.
12.Fei CW,Bai GC.Nonlinear dynamic probabilistic analysis for turbine casing radical de formation using extremum response surface method based on support vector machine.J Comput Nonlinear Dyn 2013;8(4):041004.
13.Fei CW,Bai GC.Dynamic probabilistic design for blade deformation with SVM-ERSM.Aircr Eng Aerosp Technol 2015;87(4):1–14.
14.Ren Y,Bai GC.New neural network response surface methods for reliability analysis.Chin J Aeronaut 2011;24(1):25–31.
15.Lv ZZ,Yang ZZ,Zhao J.An artificial neural network method for reliability analysis based on weighted linear response surface.Chin J Aeronaut 2006;27(6):1063–7.
16.Bai B,Bai GC.Dynamic probabilistic analysis of stress and de formation for bladed disk assemblies of aeroengine.J Cent South Univ 2014;21(10):3722–35.
17.Fei CW,Bai GC.Distributed collaborative extremum response surface method for mechanical dynamic assembly reliability analysis.J Cent South Univ 2013;20(9):2414–22.
18.Bai GC,Fei CW.Distributed collaborative response surface method for mechanical dynamic assembly reliability design.Chin J Mech Eng 2013;38(4):1160–8.
19.Zhai X,Fei CW,Zhai QG,Wang JJ.Reliability and sensitivity analyses of HPT blade-tip radical running clearance using multiply response surface model.J Cent South Univ 2014;21(11):4368–77.
20.Malhotra R,Negi A.Reliability modeling using particle swarm optimization.Int J Syst Assur Eng Manage 2013;4(3):275–83.
21.Liu DX,Cao CX.Handbook of materials for aircraft engine design.4th ed.Beijing:Aviation Industry Press;2010.p.403–17[Chinese].
22.Hua C,Fang C.Simulation of fluid–solid interaction on water ditching of an airplane by ALE method.J Hydrodyn 2011;23(5):637–42.
Zhang Chunyi is a prof essor at School of Mechanical and Power Engineering,Harbin University of Science and Technology,Harbin,China.He received his Ph.D.degree in aerospace engineering from Beihang University in 2011.His research interests are mechanical structural strength,reliability design and optimization.
Song Lukai is a Ph.D.student at School of Energy and Power Engineering,Beihang University.He received his M.S.degree in mechanical engineering from Harbin University of Science and Technology in 2016.His research interests are aeroengine structural reliability design and optimization.
Fei Chengwei is a research fellow at Department of Mechanical Engineering,The Hong Kong Polytechnic University,Kowloon,Hong Kong,China.He received his Ph.D.degree in aerospace engineering from Beihang University in 2014.His research interests are aeroengine structural strength,vibration and reliability.
Lu Cheng is a Ph.D.student at School of Aeronautics,Northwestern Polytechnical University.He received his M.S.degree in mechanical engineering from Harbin University of Science and Technology in 2016.His research interests are aircraft structural reliability design and optimization.
Xie Yongmei is an M.S.student at School of Mechanical and Power Engineering,Harbin University of Science and Technology,Harbin,China.His research interests are mechanical reliability design and optimization.
24 June 2015;revised 31 May 2016;accepted 2 June 2016
Available online 27 June 2016
Advanced multiple response surface method;
Artificial neural network;
Intelligent algorithm;
Multi-failure mode;
Reliability analysis;
Turbine blisk
*Corresponding author.Tel.+852 34002600.
E-mail addresses:zhangchunyi@hrbust.edu.cn(C.Zhang),songlukai29@163.com(L.Song),feicw544@163.com(C.Fei),liuyue501790058@qq.com(C.Lu),939406136@qq.com(Y.Xie).
Peer review under responsibility of Editorial Committee of CJA.
Production and hosting by Elsevier
http://dx.doi.org/10.1016/j.cja.2016.06.017
1000-9361?2016 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.
This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
?2016 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.Thisisan open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
 CHINESE JOURNAL OF AERONAUTICS2016年4期
CHINESE JOURNAL OF AERONAUTICS2016年4期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Numerical simulation of aerodynamic interaction for a tilt rotor aircraft in helicopter mode
- Investigation of MHD power generation with supersonic non-equilibrium RF discharge
- Experimental study on ceramic membrane technology for onboard oxygen generation
- Transition study of 3D aerodynamic configures using improved transport equations modeling
- Numerical investigation of aerodynamic flow actuation produced by surface plasma actuator on 2D oscillating airfoil
- Characterization of component interactions in two-stage axial turbine
