LARGE TIME BEHAVIOR OF A THIRD GRADE FLUID SYSTEM?
Xiaojuan CHAI(柴曉娟) Zhengzheng CHEN(陳正爭) Weisheng NIU(鈕維生)
School of Mathematical Sciences,Anhui University,Hefei 230601,China
LARGE TIME BEHAVIOR OF A THIRD GRADE FLUID SYSTEM?
Xiaojuan CHAI(柴曉娟) Zhengzheng CHEN(陳正爭) Weisheng NIU(鈕維生)?
School of Mathematical Sciences,Anhui University,Hefei 230601,China
E-mail:chaixj@ahu.edu.cn;chenzz@ahu.edu.cn;niuwsh@ahu.edu.cn
We consider the large time behavior of a non-autonomous third grade fuid system,which could be viewed as a perturbation of the classical Navier-Stokes system.Under proper assumptions,we frstly prove that the family of processes generated by the problem admits a uniform attractor in the natural phase space.Then we prove the upper-semicontinuity of the uniform attractor when the perturbation tends to zero.
third grade fuid equations;uniform attractor;upper-semicontinuity
2010 MR Subject Classifcation37L30;76D05
1 Introduction

where ν>0 is the constant kinematic viscosity,α,β are material constants and β>0.The unknown functions u,π are,respectively,the fuid velocity and the pressure.u0,f are given functions representing,respectively,the initial fuid velocity and the forcing term.Here,A is the tensor defned as A(u)=?u+(?u)Twith(?u)Tbeing the transposition of the Jacobian matrix?u,and|A(u)|2denotes tr(A2(u)).
Equation(1.1)is a special case of the following third grade fuid equation
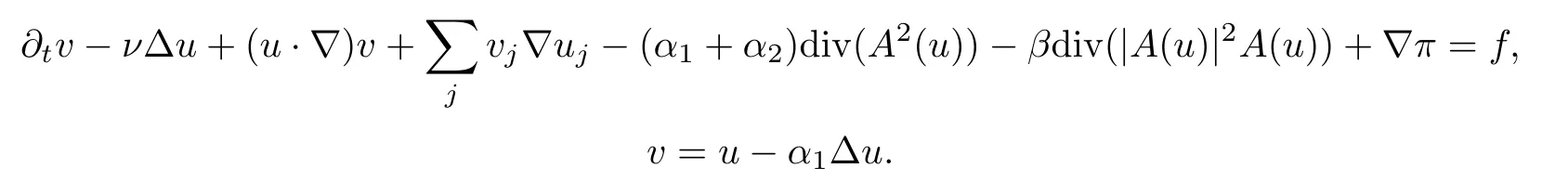
Setting α1=0 in the equation above(see[19]for the physical meaning of this assumption), we obtain equation(1.1)immediately.The third grade fuid is an important case of the non-Newtonian fuids of grade n introduced by Rivlin and Ericksen[28],for which the stress tensoris a polynomial of degree n in the frst n Rivlin-Ericksen tensors defned recursively by
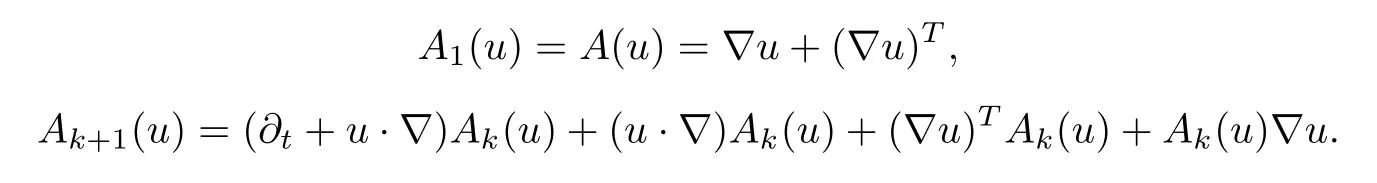
In the past years,the third grade fuid equation was studied largely.A detailed thermodynamic analysis for the model was given by Fosdick and Rajagopal in[12].In[1,30],some local existence and uniqueness results for the Cauchy problem with initial data of arbitrary size, or the global existence and uniqueness results for the Cauchy problem with small initial data were obtained in the whole space Rd,d=2,3.These results were then improved by Busuioc and Iftimie in[2],and by Paicu in[25].In[16],Hamza and Paicu studied the existence and uniqueness result of the Cauchy problem corresponding to equation(1.1)in R3.The authors proved that the Cauchy problem is globally well posed in the energy space L2(R3).Then,in[37] Zhao and his coauthors investigated the time decay results of the weak solution to the Cauchy problem considered in[16].They provided the upper and lower bounds for the time decay rate in the energy space L2(R3).More recently,in[7],we investigated the large time behavior of an autonomous conducting third grade fuid system in the presence of a magnetic feld.We proved the existence of a global attractor and an exponential attractor in proper product spaces.
In this paper,we consider the large time behavior of solutions to the non-autonomous third grade fuid system(1.1)–(1.3).The non-autonomous infnite dynamical systems were largely studied in the past decades.Paralleling to the notion of global attractors for the autonomous dynamical systems,the notions of uniform attractors and pullback attractors were proposed and well developed for non-autonomous dynamical systems.The existence and some properties (such as the structure,the dimension and the stability property,ect.)of uniform attractors or pullback attractors were investigated for various non-autonomous systems,such as the incompressible Navier-Stokes systems,reaction difusion systems,damped wave equations and so on, see[8–10,15,18,27,39]and the large amount of references therein.In the present paper,we will mainly consider the existence of uniform attractors for the non-autonomous third grade fuid system(1.1)–(1.3).
Throughout the paper,we make the assumption that the initial data and forcing term are zero-spatial-mean functions(R??dx=0 for ?=u0,f),so that the solutions have zero spatial mean,which allows us using the Poincar′e inequality.As we are interested in the nonautonomous case,thus we assume that the forcing term f is time dependent.With proper assumptions on the material constants α,β and the forcing term f,we frst provide the existence and uniqueness result for the system with L2initial data.Then,we prove the existence of a uniform attractor in L2.
Note that when the material constants α,β in(1.1)–(1.3)tend to zero,the system converges formally to the Navier-Stokes system
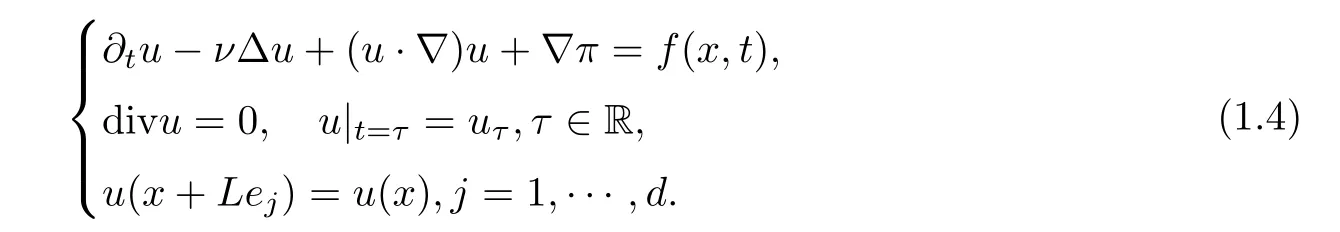
One may expect that the solutions of system(1.1)–(1.3)converge to solutions of the Navier-Stokes system,and so does the corresponding attractor.Thus,the second aim of this paper isto provide positive answers to the above two guesses.We prove that in the 2D case,the unique solution and the uniform attractor of system(1.1)–(1.3)converge respectively to the unique solution and the uniform attractor for the Navier-Stokes system.
It is worth recalling that these issues for some other modifed Navier-Stokes equations were considered largely in the literatures.For example,in[13,17],the authors proved the convergence of weak solutions and global attractors for the Navier-Stokes-α system to those of the Navier-Stokes system as α tends to zero.In[35],the convergence of the uniform attractor for the Navier-Stokes-α system to that of the Navier-Stokes system was explored.In[11,34], the authors studied the convergence of the trajectory attractors of the Leray-α system and the Camassa-Holm system to the trajectory attractor of the Navier-Stokes system.In[5,14,38], the convergence of solutions and global attractors for the bipolar viscous non-Newtonian fuid system to those of Navier-Stokes system was investigated,while in[26]the convergence of solutions and global attractors for the second grade fuid system to those of the Navier-Stokes system was studied.
Now let us talk about the organization of the paper.In Section 2,we provide some preliminaries about the function spaces and uniform attractors.In Section 3,we prove the existence of the uniform attractor for system(1.1)–(1.3)in dimensions two and three,while in Section 4, we investigate the convergence of the weak solution and the uniform attractor as α,β tend to zero in dimension two.
2 Preliminaries
2.1Function Spaces
For the domain ?=[0,L]d,d=2,3,let C∞p(?)be the space of restrictions to ? of infnitely diferentiable functions that are L-periodic.The Sobolev spaceis the completion ofwith respect to the norm of Wk,q(?).LetFor any function space X,we denote by X the space Xd,endowed with the product structure,for example,We defne
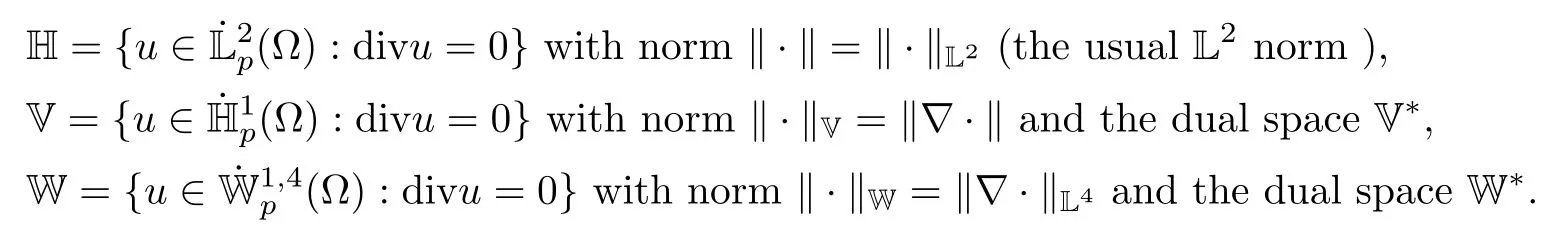
Let A(from V to V?)B(u,v)(from V×V into V?)be,respectively,the standard Stokes operator and the bilinear operator defned as
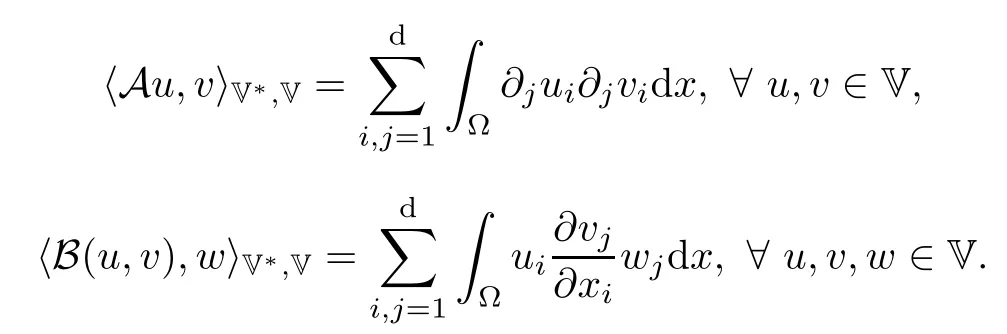
Defne the operators K(·),J(·),T(·)from W into W?as
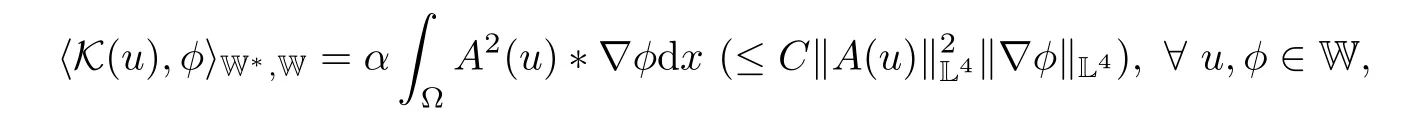

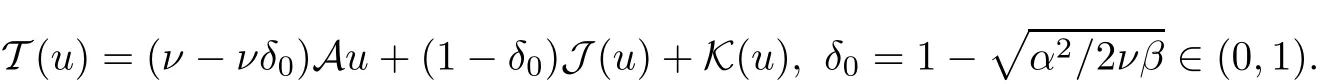

The following Korn’s inequality plays an essential role in our analysis.
Lemma 2.1(see[6]) Assume that 1 Then there exist two positive constants c0,c1depending on q,?,such that 2.2Processes and Uniform Attractors We frst give a short review on processes and uniform attractors.Let Σ be a parameter set, and let E be a Banach space.Let{Uσ(t,τ)}t≥τ,τ∈R,σ∈Σ be a family of processes in Banach space E,that is,for any σ∈Σ,the two parametric family of operators Uσ(t,τ):E→E,t≥τ,τ∈R satisfying here σ is often called the symbol and Σ is called the symbol space. Defnition 2.2(see[8]) A set B0?E is said to be a uniformly absorbing set for the family of processes{Uσ(t,τ)}t≥τ,τ∈R,σ∈Σ if for any τ∈R and any B?E bounded,there exists a T=T(τ,B)≥τ such that Uσ(t,τ)B?B0for t≥T(τ,B)and for all σ∈Σ. Defnition 2.3(see[8]) A set P?E is said to be a uniformly attracting set for the family of processes{Uσ(t,τ)}t≥τ,τ∈R,σ∈Σ if for any fxed τ∈R and set B?E bounded, Defnition 2.4(see[8]) A closed set AΣ?E is said to be a uniform(w.r.t.σ∈Σ) attractor of the family of processes{Uσ(t,τ)}t≥τ,τ∈R,σ∈Σ,if it is uniformly attracting and is contained in any other closed uniformly attracting set(hence the uniform attractor is unique, if it exists). Defnition 2.5(see[8]) A family of processes{Uσ(t,τ)}t≥τ,τ∈R,σ∈Σ on a complete metric space X is said to be uniformly(w.r.t.σ∈Σ)asymptotically compact if and only if for any fxed τ∈R,a bounded sequence{?n}∞n=1?X,{σn}∞n=1?Σ,and any{tn}∞n=1?Rτwith tn→∞as n→∞,the sequence{Uσn(tn,τ)?n}∞n=1is precompact in X. Defnition 2.6(see[8]) The kernel K of a process U(t,τ)consists of all bounded trajectories of the process,i.e., The set K(s)={u(s)|u(·)∈K}is called the kernel section of the process at time t=s,s∈R. Let Σ be a subset of a Banach space. Defnition 2.7(see[8]) A family of processes{Uσ(t,τ)}t≥τ,τ∈R,σ∈Σ is said to be (E×Σ,E)weakly continuous if for any t≥τ,τ∈R,the mapping(u,σ)→Uσ(t,τ)u is weakly continuous. Theorem 2.8(see[20,21]) Let Σ be a weakly compact set.Assume that{T(h)}h≥0is a semigroup of weakly continuous operators in Σ such that T(h)Σ=Σ,?h>0,and the following translation identity holds Moreover,assume that{Uσ(t,τ)}t≥τ,τ∈R,σ∈Σ, (i)is(E×Σ,E)weakly continuous, (ii)possesses a bounded uniformly(w.r.t.σ∈Σ)absorbing set B0, (iii)is uniformly(w.r.t.σ∈Σ)asymptotically compact. Then the family of processes admits a compact uniform(w.r.t.σ∈Σ)attractor AΣsatisfying here Kσ(s)is the section,at t=s,of the kernel Kσof the process Uσ(t,τ)with symbol σ. Moreover,Kσ(s)is nonempty for all σ∈Σ. In this section,we prove the existence of a uniform attractor for the system(1.1)–(1.3). Defnition 3.1Let uτ∈H,be given(Rτ=[τ,∞)).A weak solution of the system(1.1)–(1.3)is a functionwithsuch that for any ?∈W,T≥τ, Let X be a Banach space.A functionis translation bounded in(denoted byif Theorem 3.2Assume that uτ∈Hand ν,β>0 satisfying|α|Then the system(1.1)–(1.3)admits a unique weak solution u∈C(Rτ;H)∩L∞(Rτ;H)∩withsuch that,for any t≥τ, where the positive constants C0,C1,C2depend on α,β,ν,but is independent of t. If in addition uτ∈V,f∈L2b(R;H)and|α|then for any t≥τ, ProofThe existence result can be obtained by the standard Galerkin method,and the calculations are totally parallel to that of Theorem 1.1 in[16].Thus we omit the details for concision,and just provide the proof of the regularity results.We perform the formal calculations,which could be justifed rigorously by the Galerkin expansion.Multiplying(1.1) by u,it is not difcult to obtain that Note that A(u)is symmetric.We have From the Cauchy-Shwatz inequality and the fact that we deduce that where Using the Poincar′e inequality and Gronwall’s lemma,we deduce from(3.6)that for any fxed t>τ, and then Hence,we obtain(3.2),(3.3). Now if uτ∈V,f∈L2b(R;H)andwe multiply(1.1)by??u to obtain that Note that where aij=aij(u)=?iuj+?jui,i,j=1,···,d.Since aij=aji,we deduce from(3.10)by integration by parts that Moreover, Therefore,setting ε1=(∈(0,1))and taking ε=νε1,we deduce from(3.9), (3.11)and(3.12)that In the 2D case,since we have Similar to the deduction of(3.7),by the Poincar′e inequality and Gronwall’s lemma we can deduce that Integrating(3.14),we then get Combining(3.15)with(3.16),we obtain(3.4)immediately. In the 3D case,by H¨older’s inequality and the Gagliardo-Nirenberg inequality we deduce that where the positive constants C3,C4arise,respectively,from Gagliardo-Nirenberg inequalities and Young’s inequality.Thus taking the inequality above into(3.13),we deduce that Integrating(3.17)between s and t+1(τ≤t≤s Now integrating with respect to s on(t,t+1),we obtain for some positive constant C5,which is independent of t.At last,integrating(3.17)and using Korn’s inequality,(3.7)and(3.8),we obtain that for some positive constant C6.Now,combining(3.18)and(3.19),we obtain(3.4)immediately. Thanks to(3.2),the family of processes defned above possesses a uniform absorbing set B0in H,which can actually be characterised as the ball centered at zero with radius The following proposition implies the weak continuity of the family of processes defned above. ProofFor fxed τ∈R,we set un(t)=Ufn(t,τ)unτand u(t)=Uf(t,τ)uτ.Note that un(t) satisfes Taking unas a test function,similar to(3.6)we obtain that by which we can deduce that Note that Hence Thanks to the Aubin-Simon type compactness results,see for example[29,31,32],there exists a vector-valued functionsuch that,up to subsequences, Now let us take ?∈W as a test function in(3.20)to obtain that Similar to the Navier-Stokes equations,it is easy to derive the following convergence results On the other hand,thanks to[16],we know that the operator T1:W→W?defned as is a monotone operator.Thus,we can use the standard monotone operator theory as[3,16], see also[4,23,24],to derive the following convergence result And then we obtain that e u is a weak solution to the system(1.1)–(1.3)with initial data uτand external force f.By the uniqueness of weak solution,we conclude that e u≡u.By a contradiction argument,we can easily obtain that the whole sequence unconverges to u in the sense of(3.24). Now,for any fxed T>τ and v∈W,by(3.22)we know that(un(t),v)(.=R?un(t)vdx) is uniformly(w.r.t.n)bounded on[τ,T].On the other hand,by(3.23),we deduce that for for some positive constant M0>0,which implies that(un(t),v)is equicontinuous.Therefore by the Azel′a-Ascoli theorem we obtain that By the density of W in H,we then obtain the result of Proposition 3.3 immediately. ? The proposition below implies the asymptotic compactness of the family of processes. Proposition 3.4Let{Uf(t,τ)}t≥τ,τ∈R,f∈Hw(f0)be the family of processes corresponding to(1.1)–(1.3)defned above,and let B0be the uniform absorbing set given above. Assume that f0is normal.Then for any fxed τ∈R there is a T0=T(τ,B0)≥τ such that∪f∈Hw(f0)Uf(T,τ)B0is precompact in H for any T≥T0. Thanks to Theorem 3.1,we know that for any fxed t≥τ, That is,for any T>τ, Therefore,we conclude that,up to a subsequence,un(s)converges to u(s)in L2(?)for almost all s∈[τ,T].Especially,for any 0<η<1 there exists ?∈[T?η,T]such that Note that wn(t)=un(t)?u(t)satisfes Now,we multiply the above equation by wnand integrate with respect to the space variable. Bearing in mind that J,T are monotone operators,and we deduce that for some positive constants C7,Cε.Here we use the 2D or 3D Ladyzhenskaya inequality(see, e.g.[29]) and Young’s inequality.From(3.32)we are ready to obtain Note that(3.7)implies that Using Korn’s inequality and the Gagliardo-Nirenberg inequality we can deduce from(3.8)that,for T≥T1(τ,B0)+1, Combining(3.30)and(3.35),we obtain that for any ?>0 there exists N0such that On the other hand,by(3.8),(3.29)and Korn’s inequality,we have Hence for any ?>0,we can take ε small enough such that At last,note that Combining(3.34),(3.36),(3.37)and(3.38),we conclude that for any T≥T1(τ,B0)+1,up to subsequences, as n tends to infnity. As a corollary,we have Corollary 3.5The family of processes{Uf(t,τ)}t≥τ,τ∈R,f∈Hw(f0)is uniformly(w.r.t.f) asymptotically compact in H. ProofThanks to(3.7),for any bounded subset B of H,there is a time t0=t(τ,B)such that Since Proposition 3.4 then implies that∪f∈Hw(f0)Uf(t,t0)B0is precompact for t large enough,saying that t≥ T0>t0.Therefore∪f∈Hw(f0)Uf(t,τ)B is precompact for t≥ T0.That is to say for any fxed t≥T0,any bounded sequence{unτ}∞n=1?B,{fn}∞n=1?Hw(f0),the sequence {Ufn(t,τ)unτ}∞n=1has convergent subsequences.Using the standard diagonal method,we can easily obtain that for any bounded sequence{unτ}∞n=1,{fn}∞n=1?Hw(f0),and any{tn}∞n=1?Rτwith tn→ ∞ as n→ ∞,the sequence{Uσn(tn,τ)unτ}∞n=1has convergent subsequences. Therefore,the family of processes{Uf(t,τ)}t≥τ,τ∈R,f∈Hw(f0)is uniformly asymptotically compact. With the results above,we are ready to obtain the main result of this section by applying Theorem 2.1. here Kf(s)is the section at t=s of the kernel Kffor the process Uf(t,τ).Moreover,Kf(s)is nonempty for all f∈Hw(f0). In this section,let us consider the convergence of the solution and the uniform attractor of system(1.1)–(1.3)to those of the Navier-Stokes system.Since the existence and uniqueness of solutions remain an open problem for the 3D Navier-Stokes system,we will mainly focus on the 2D case here.We rewrite(1.1)–(1.3)in the 2D case as On the other hand,it is well known that under spatial periodic boundary conditions,the Navier-Stokes system(1.4)in the 2D torus admits a unique weak solution u∈C(Rτ;H)∩if the initial data uτ∈H and the external forceAnd the processis well defned in H,Moreover,if f0∈is normal,the family of processesadmits a unique uniform attractorin H[20,21]. Next,let us consider the convergence of the solution and the uniform attractor of system (4.1)to those of the 2D Navier-Stokes system. Theorem 4.1Assume that ν,β>0,|α|Let B be a bounded subset of V.Then for any β∈(0,1)and any T≥τ,there exists a positive constant C= C(α,β,ν,T,Bsuch that ProofLet uβ(t)=Uβf(t,τ)uτ,u0(t)=U0f(t,τ)uτbe,respectively,the solution of the third grade fuid system(1.1)–(1.3)and the Navier-Stokes system(1.4)with the same initial data u(τ)=uτ∈B and the same external termThen it is obvious that w(t)=uβ(t)?u0(t)satisfes the following equation Multiplying by w and integrating,it yields Using the Ladyzhenskaya inequality(3.33)and Korn’s inequality,we deduce that Thus we have Note that for the 2D Navier-Stokes equations,it is easy to deduce that(see,e.g.[20,29,33]) for any t≥τ.On the other hand,by(3.14),we can obtain that Taking(4.7),(4.8)into(4.6),it yields where Setting we get(4.2). where M is a positive constant such that kψkV≤M for all ψ∈B.It is obvious that the right hand side of(4.11)is independent of α,β.Therefore,we can take the positive constant C in (4.2)as it and complete the proof of Theorem 4.1. Theorem 4.2Assume that ν,β>0,|α|for some 0<δ<1.Letbe,respectively,the uniform attractor of the families of processes generated by the third grade fuid system(4.1)and the 2D Navier-Stokes system(1.4).Then we have ProofNote that for a fxed τ∈R and t>τ. Next,let us consider(4.13)–(4.15)one by one.On the one hand,thanks to(3.7)and(3.15), we know that the uniform attractoris uniformly(w.r.t.β∈(0,1])bounded in H and V.Since the uniform attractoris uniformly attracting in H,for any ?>0,there is atime T0=T(?)>τ such that for any τ≤t≤T0.Moreover,under the assumption C(α,β,ν,T0?τ,B,f)could be chosen to be independent of α,β,and therefore is uniformly bounded as β→0. At last,let us consider(4.15).Let Thanks to the discussions in the sections above,we know that{Sβ(t)}t≥0is a weakly continuous and weakly compact semigroup on H×Hw(f0).Performing the analysis as in[8,20],we can show that the semigroup Sβ(t)possesses a weakly compact global attractorAβwith Moreover,let P be the projection from H×Hw(f0)to H.We have By the invariance of the global attractor(Sβ(t)Aβ=Aβ,?t≥0),for any(u,f)∈Aβ, for any t≥τ,f∈Hw(f0)and u∈From(4.20)and(4.21),we deduce that for any t≥τ,f∈Hw(f0),which implies thatNow combining(4.16),(4.17)with(4.22),we get The proof is completed. AcknowledgementsThe authors would like to thank Professor Dong Boqing for the discussions on the model. [1]Amrouche C,Cioranescu D.On a class of fuids of grade 3.Int J Non-Linear Mech,1997,32:73–88 [2]Busuioc A V,Iftimie D.Global existence and uniqueness of solutions for the equations of third grade fuids. Int J Non-Linear Mech,2004,39:1–12 [3]Busuioc A V,Iftimie D,Paicu M.On steady third grade fuids equations.Nonlinearity,2008,21:1621–1635 [4]Babin A V,Vishik M I.Attractors of Evolution Equations.Amsterdam:North-Holland,1992 [5]Bloom F.Lower semicontinuity of the attractors of non-Newtonian fuids.Dynam Syst Appl,1995,4: 567–579 [6]BelloutH,Bloom F.IncompressibleBipolarand Non-Newtonian ViscousFluidFlow.Cham: Birkh¨auser/Springer,2014 [7]Chai X J,et al.Large time behavior for a class of magnetohydrodynamic fow of a third grade fuid.accepted [8]Chepyzhov V V,Vishik M I.Attractors for Equations of Mathematical Physics.Providence,RI:Amer Math Soc,2002 [9]Carvalho A,Langa J,Robinson J C.Attractors for Infnite Dimensional Non-Autonomous Dynamical Systems.New York:Springer,2013 [10]Cheskidov A,Lu S S.Uniform global attractors for the nonautonomous 3D Navier-Stokes equations.Adv Math,2014,267:277–306 [11]Chepyzhov V V,Titi E S,Vishik M I.On the convergence of solutions of the Leray-α model to the trajectory attractor of the 3D Navier-Stokes system.Discrete Contin Dyn Syst,2007,17:481–500 [12]Fosdick R L,Rajagopal K R.Thermodynamics and stability of fuids of third grade.Proc R Soc London Ser A,1980,369:351–377 [13]Foias C,Holm D D,Titi E S.The three dimensional viscous Camassa-Holm equations,and their relation to the Navier-Stokes equations and turbulence theory.J Dynam Difer Equ,2002,14:1–35 [14]Guo C X,Guo B L.The convergence of non-Newtonian fuids to Navier-Stokes equations.J Math Anal Appl,2009,357:468–478 [15]Haraux A.Systemes Dynamiques Dissipatifs et Applications.Paris:Masson,1991 [16]Hamza M,Paicu M.Global existence and uniqueness result of a class of third grade fuids equations. Nonlinearity,2007,20:1095–1114 [17]Ilyin A A,Titi E S.Attractors for the two dimensional Navier-Stokes-α model:an α-dependence study.J Dynam Difer Equ,2003,15:751–778 [18]Kloeden P E,Rasmussen M.Nonautonomous Cynamical Systems.Mathematical Surveys and Monographs, 176.Providence,RI:American Mathematical Society,2011 [19]Ladyzhenskaya O A.New equations for the description of the motions of viscous incompressible fuids,and global solvability for their boundary value problems.Trudy Mat Inst Steklov,1967,102:85–104 [20]Lu S S,Wu H Q,Zhong C K.Attractors for nonautonomous 2D Navier-Stokes equations with normal external forces.Discrete Contin Dyn Syst,2005,13:701–719 [21]Lu S S.Attractors fo nonautonomous 2D Navier-Stokes equation with less regular normal forces.J Difer Equ,2006,230:196–212 [22]Lu S S.Attractors for nonautonomous reaction-difusion system with symbol without strong translation compactness.Asymp Anal,2007,54:197–210 [23]Lions J L.Quelques M′ethodes de R′esolution des Probl`emes aus Limites Non Lin′earires.Paris:Dunod, 1969 [24]Ladyzhenskaya O A.Mathematical Problems of the Dynamics of a Viscous Incompressible Liquid.Moscow: Nauka,1970 [25]Paicu M.Global existence in the energy space of the solutions of a non-Newtonian fuid.Physica D,2008, 237:1676–1686 [26]Paicu M,Raugel G,Rekalo A.Regularity of the global attractor and fnite-dimensional behavior for the second grade fuid equations.J Difer Equ,2012,252:3695–3751 [27]Qin Y M,Yang X G,Liu X.Pullback attractors for the non-autonomous Benjiamin-Bona-Mahony equations in H2.Acta Math Sci,2012,32B:1338–1348 [28]Rivlin R S,Ericksen J L.Stress-deformation relations for isotropic materials.J Ration Mech Anal,1955, 4:323–425 [29]Robinson J C.Infnite-dimensional dynamical systems//An Introduction to Dissipative Parabolic PDEs and the Theory of Global Attractors.Cambridge:Cambridge University Press,2001 [30]Sequeira A,Videman J.Global existence of classical solutions for the equations of third grade fuids.J Math Phys Sci,1995,29:47–69 [31]Simon J.Compact sets in the space Lp(0,T;B).Ann Mat Pura Appl,1987,146:65–96 [32]Temam R.Navier-Stokes Equations,Theory and Numerical Analysis.North-Holland,1979 [33]Temam R.Infnite-dimensional Dynamical Systems in Mechanics and Ahysics.New York:Springer,1997 [34]Vishik M I,Titi E S,Chepyzhov V V.On convergence of trajectory attractors of the 3D Navier-Stokes-α model as α approaches 0.Sbornik Math,2007,198:1703–1736 [35]Yue G C.Zhong C K,On the convergence of the uniform attractor of 2D NS-α model to the uniform attractor of 2D NS system.J Comput Appl Math,2010,233:1879–1887 [36]Zelik S.Strong uniform attractors for non-autonomous dissipative PDEs with non translation-compact external forces.Discrete Contin Dyn Syst Ser B,2015,20:781–810 [37]Zhao C D,Liang Y,Zhao M.Upper and lower bounds of time decay rate of solutions to a class of incompressible third grade fuid equations.Nonlinear Anal,2014,12:229–238 [38]Zhao C D,Duan J Q.Convergence of global attractors of a 2D non-Newtonian system to the global attractor of the 2D Navier-Stokes system.Sci China Math,2013,56:253–265 [39]Zhao C D,Jia X L,Yang X B.Uniform attractor for nonautonomous imcompressible non-Newtonian fuid will a new class of external forces.Acta Math Sci,2011,31B:1803–1812 ?Received August 8,2015;revised May 2,2016.Supported by NSFC(11301003,11426031,11501560),the Research Fund for Doctor Station of the Education Ministry of China(20123401120005),NSF of Anhui Province (1308085QA02). ?Corresponding author:Weisheng NIU.
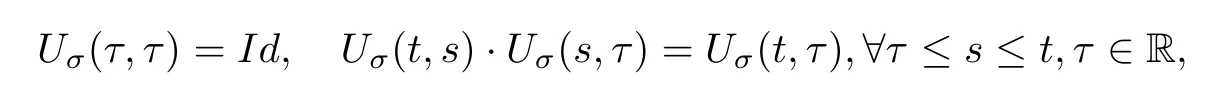
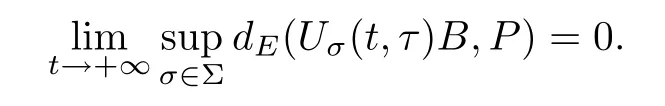
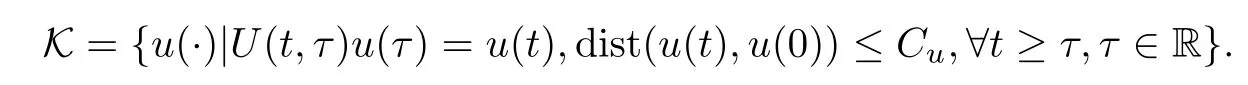
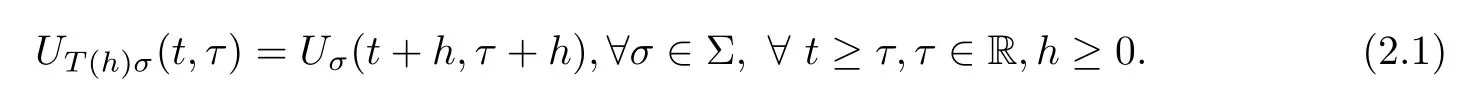
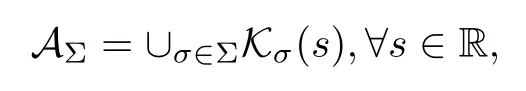
3 Existence of Uniform Attractors
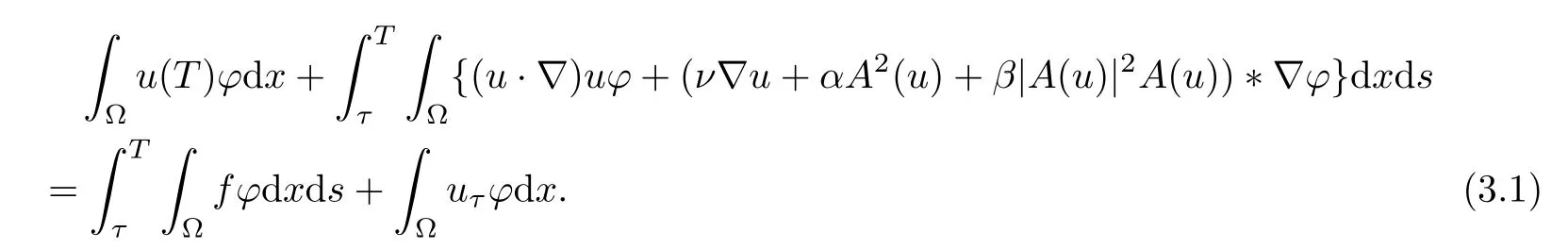

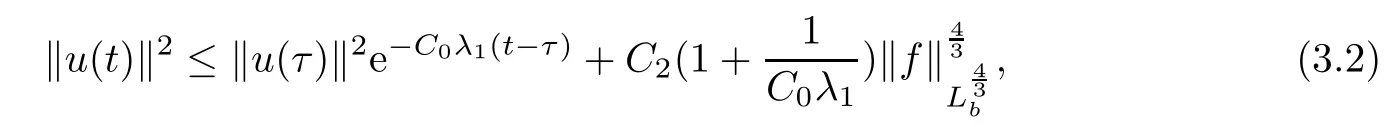
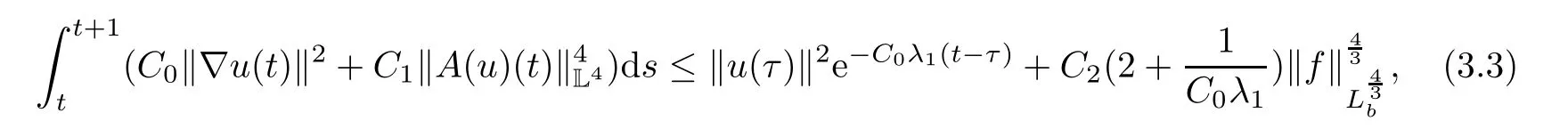
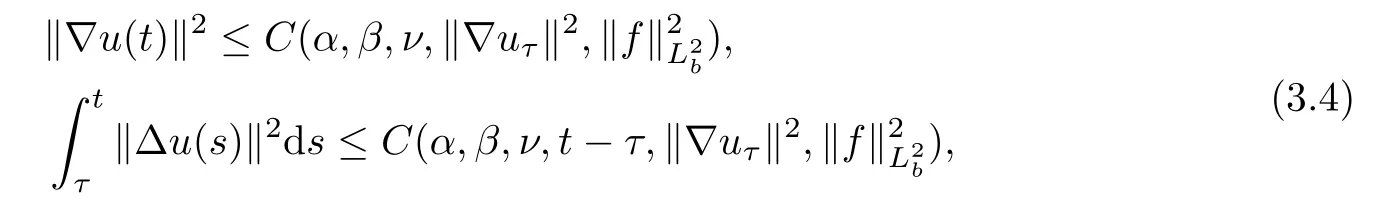
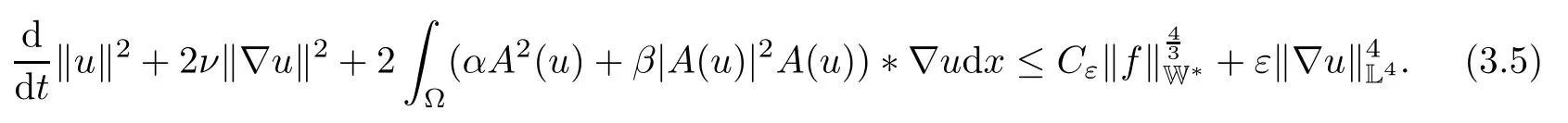
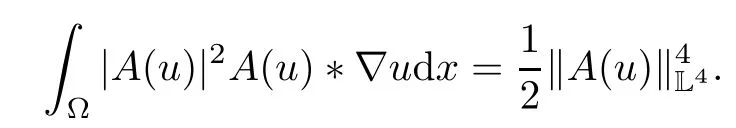
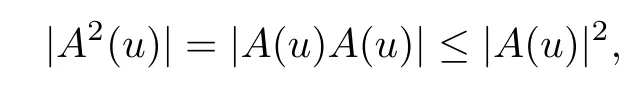


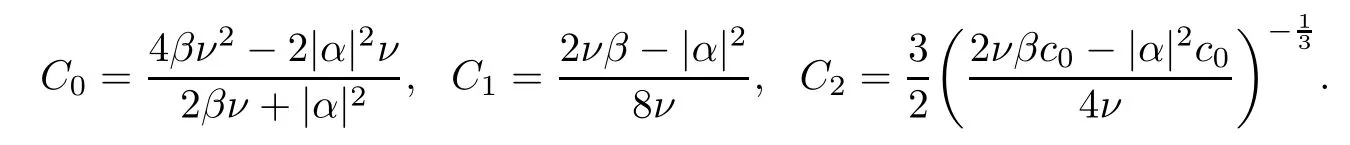
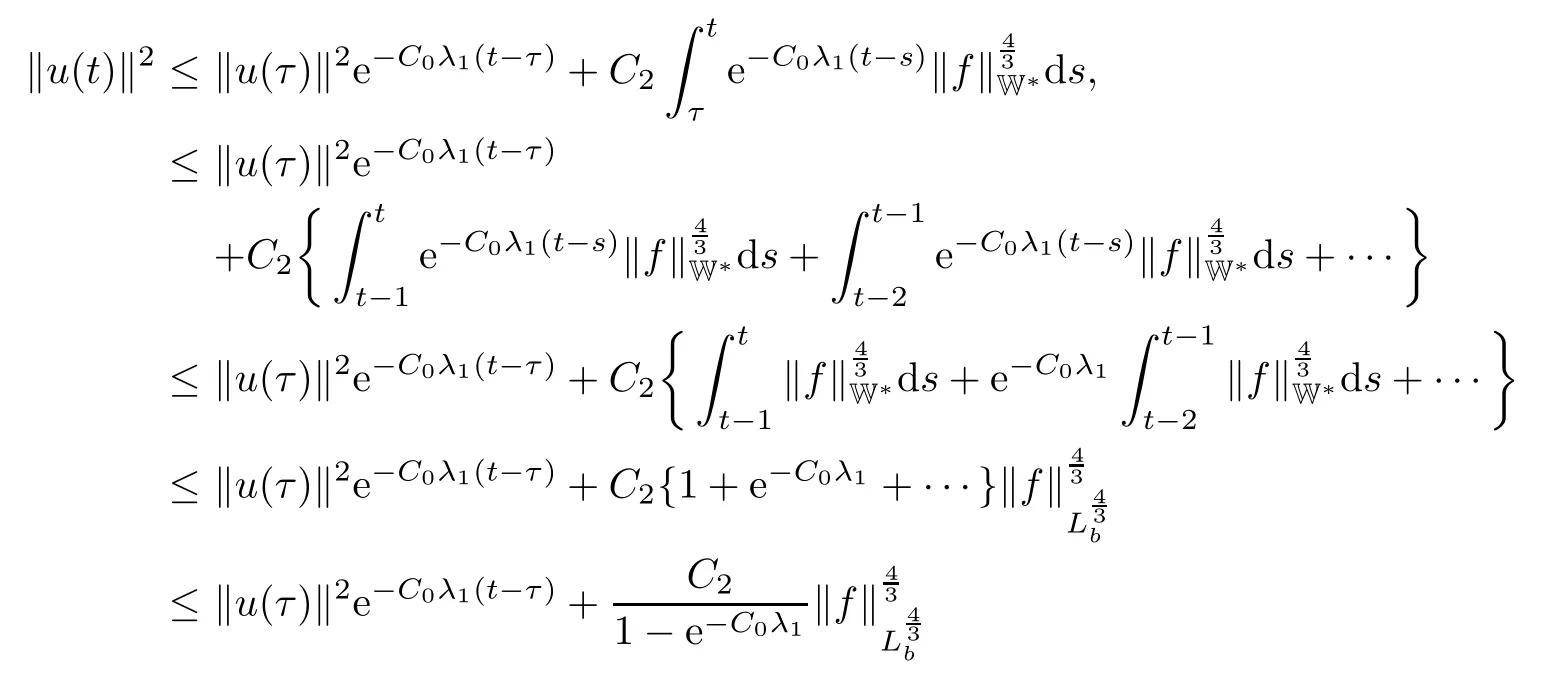
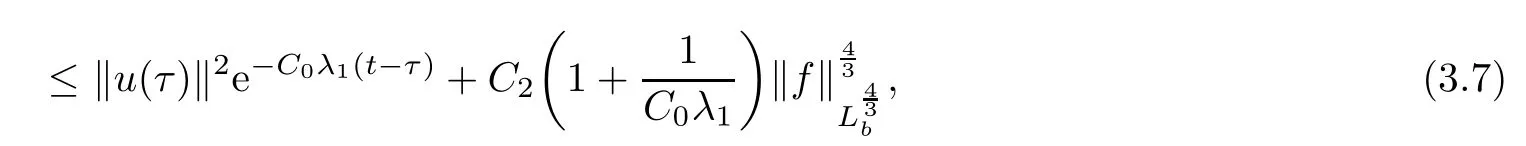
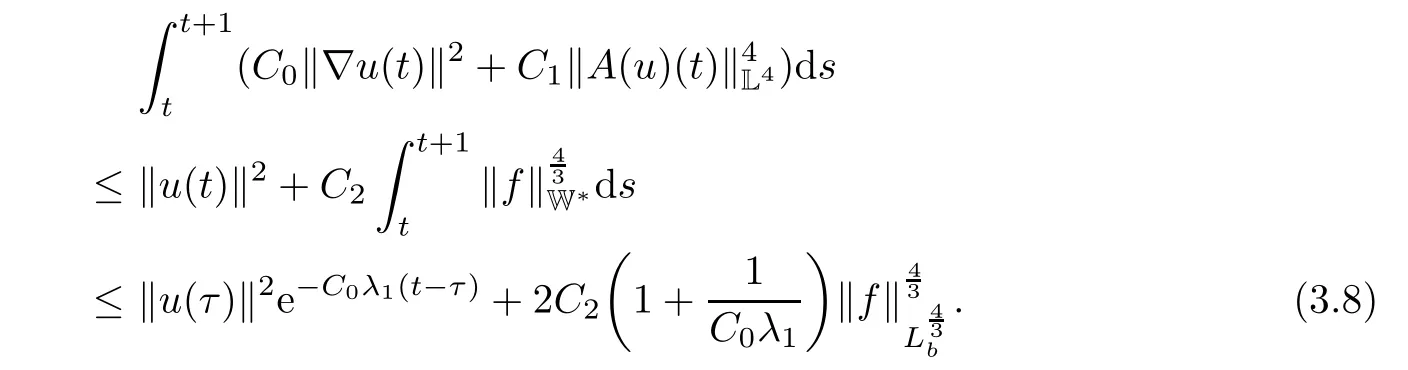
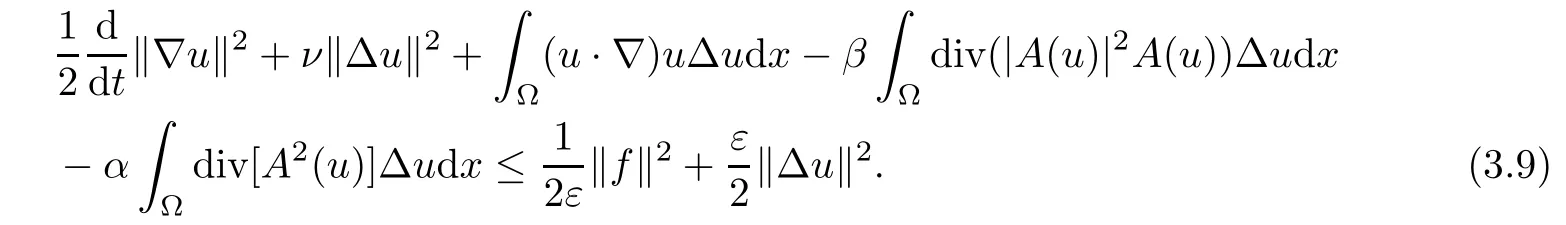
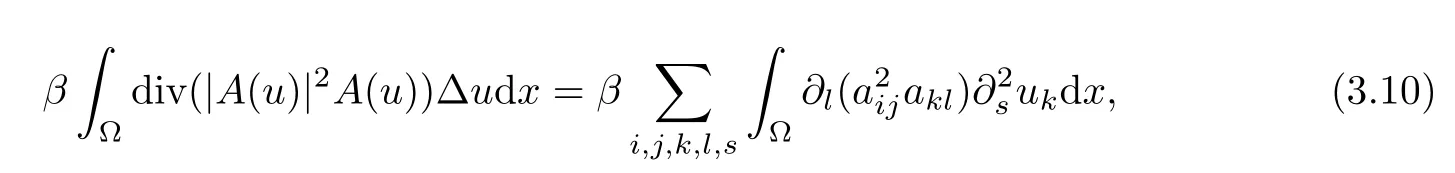
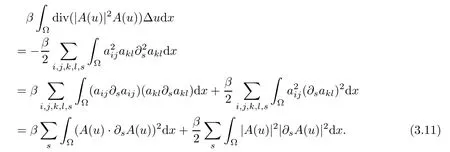
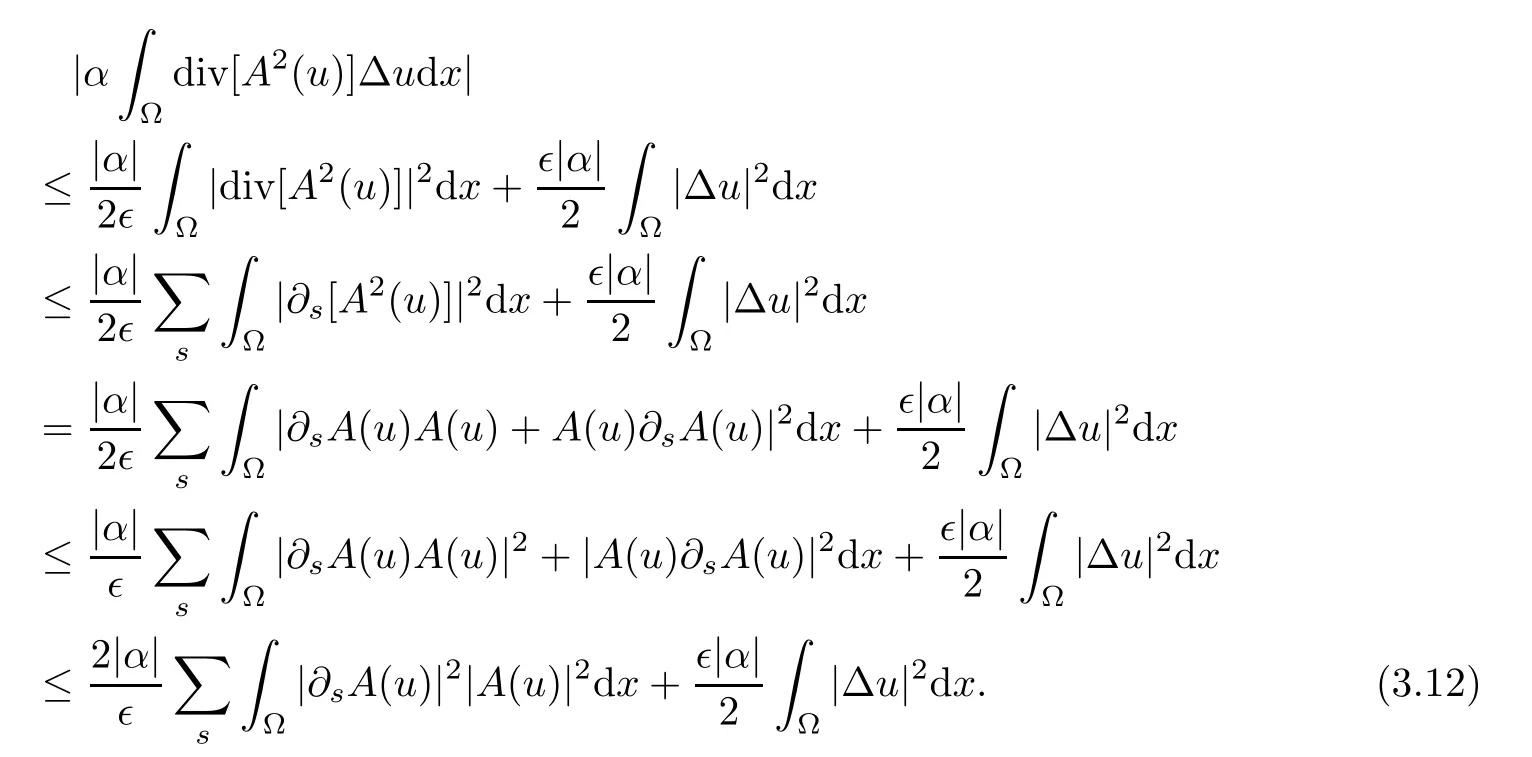
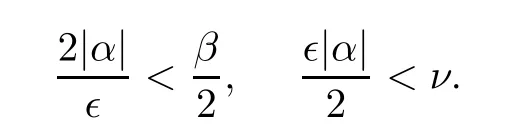

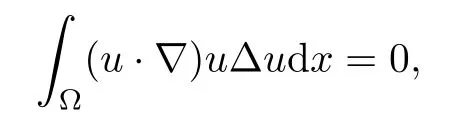
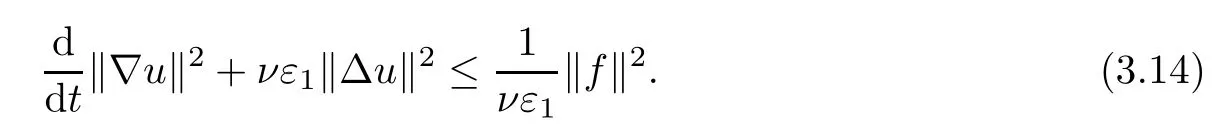
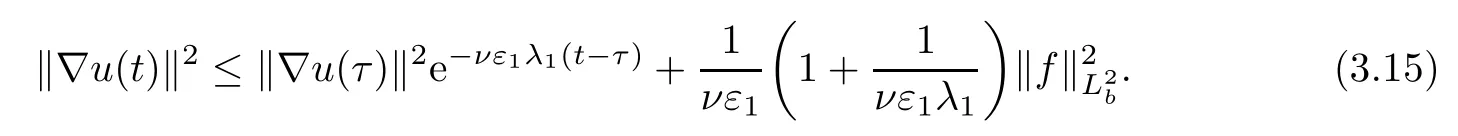
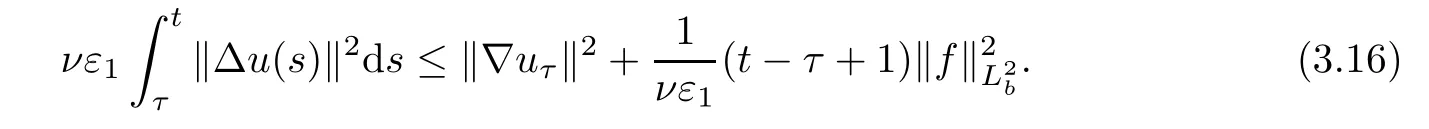
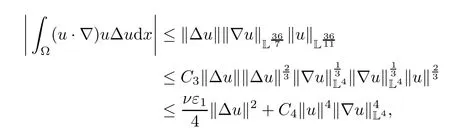
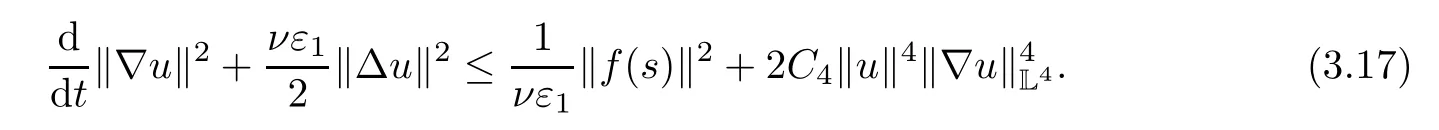

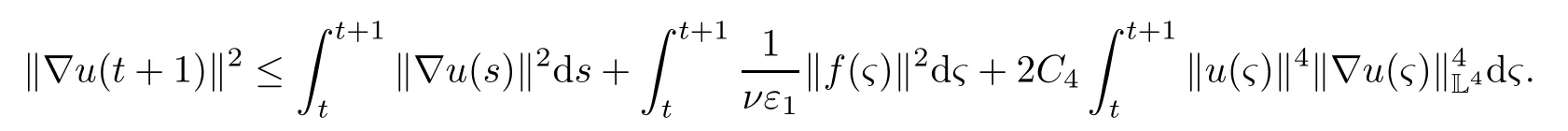

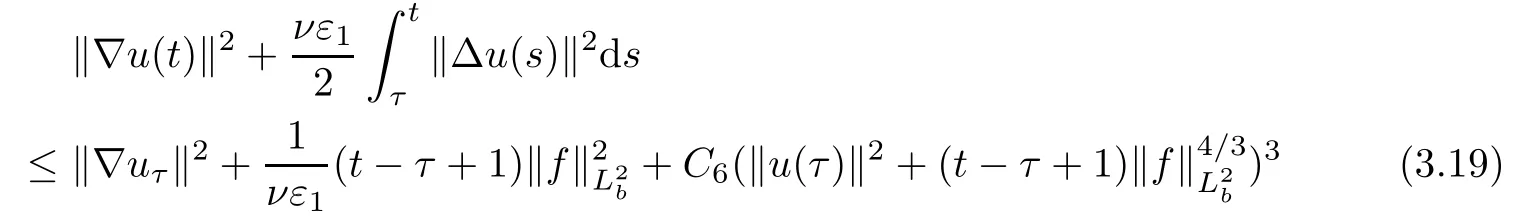
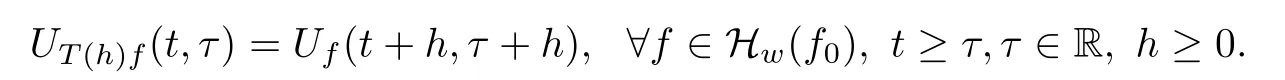
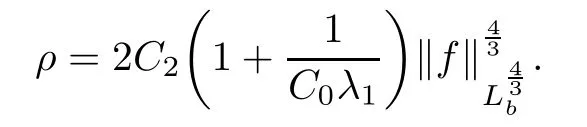
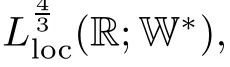
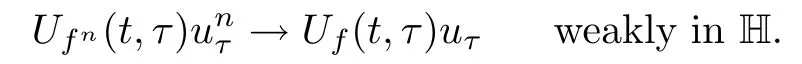

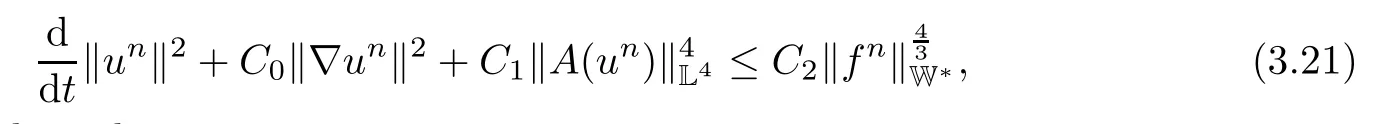
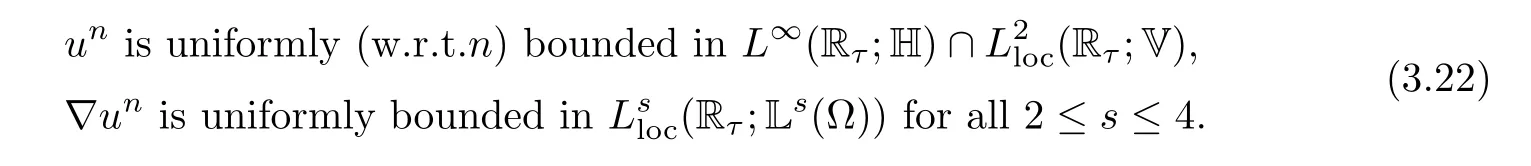

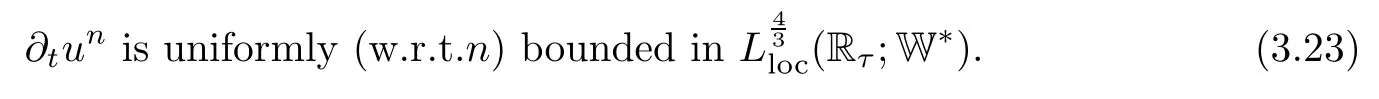

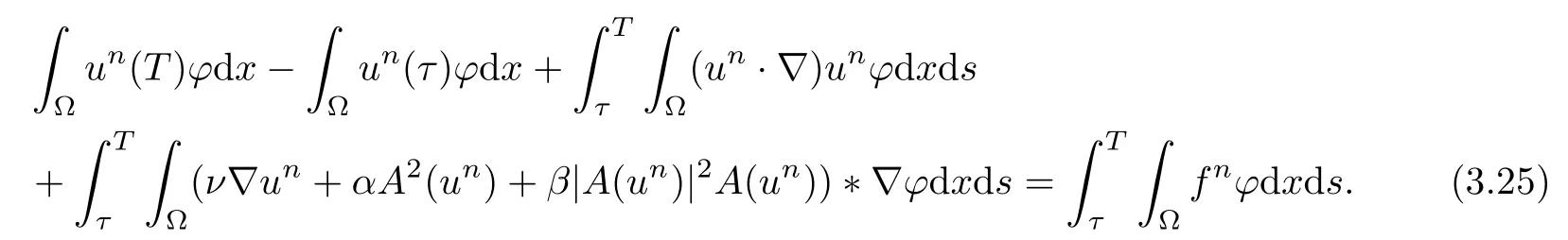
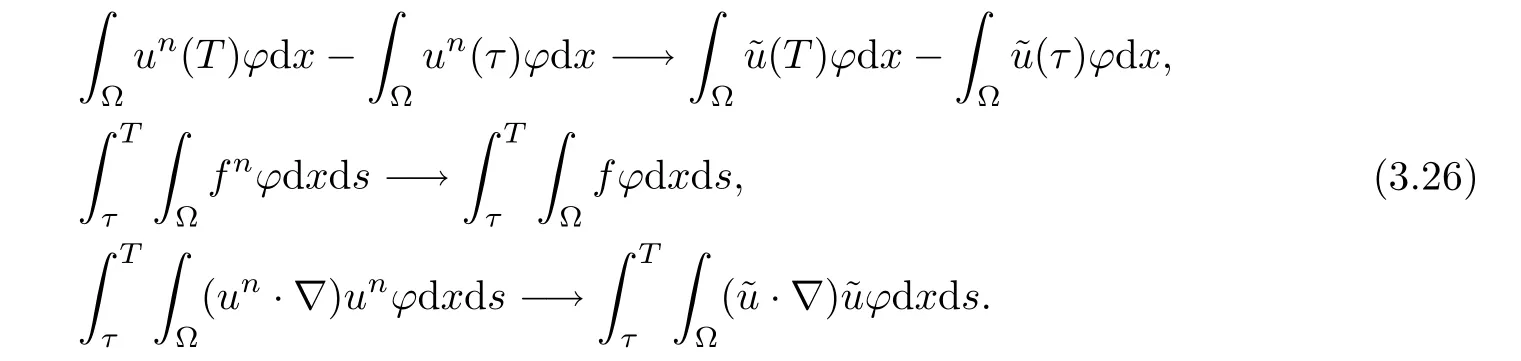


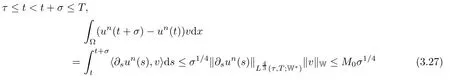
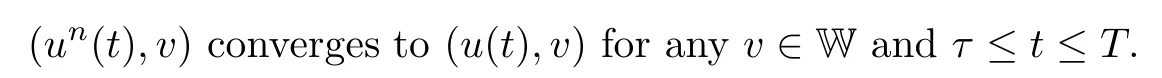
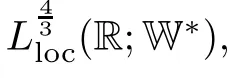
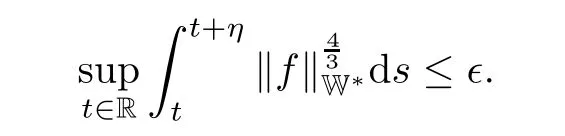

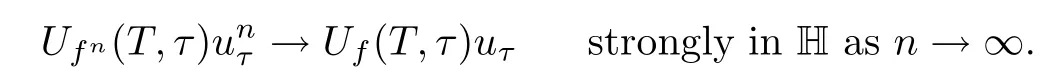
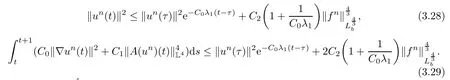
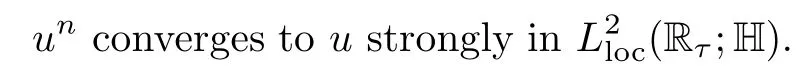
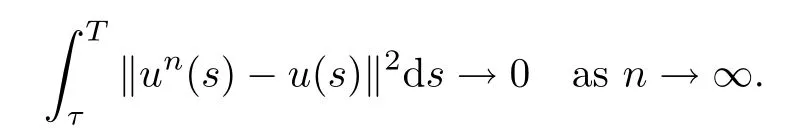

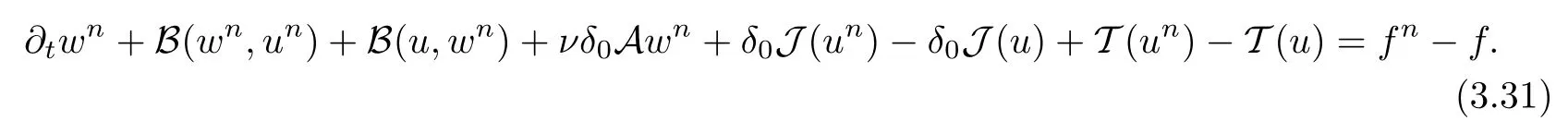
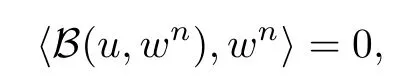
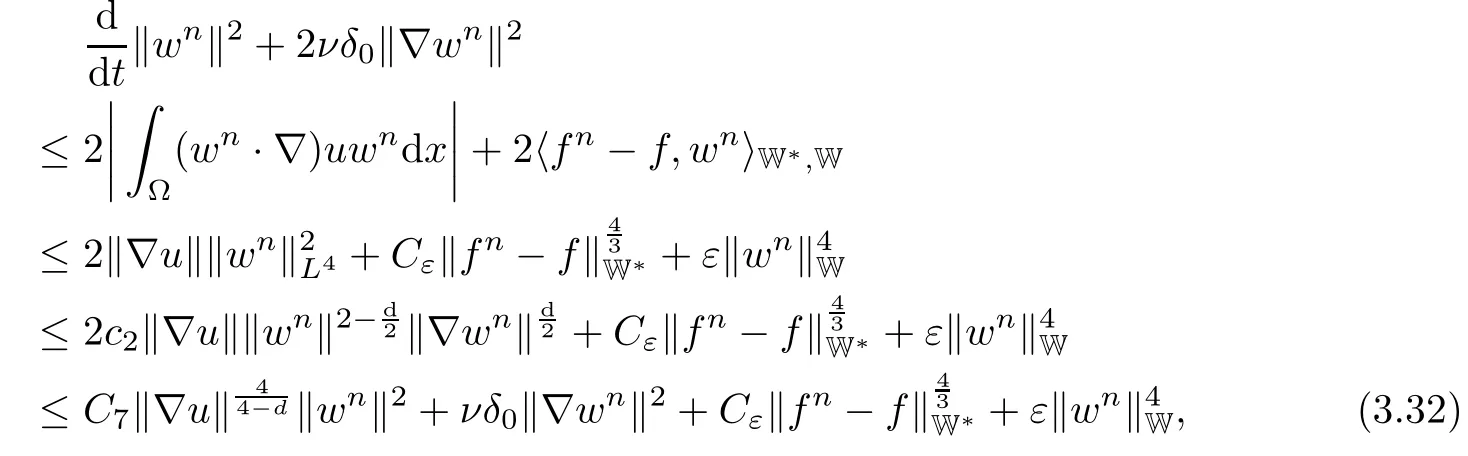
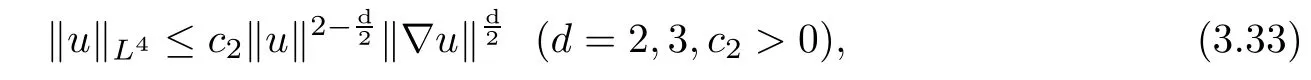
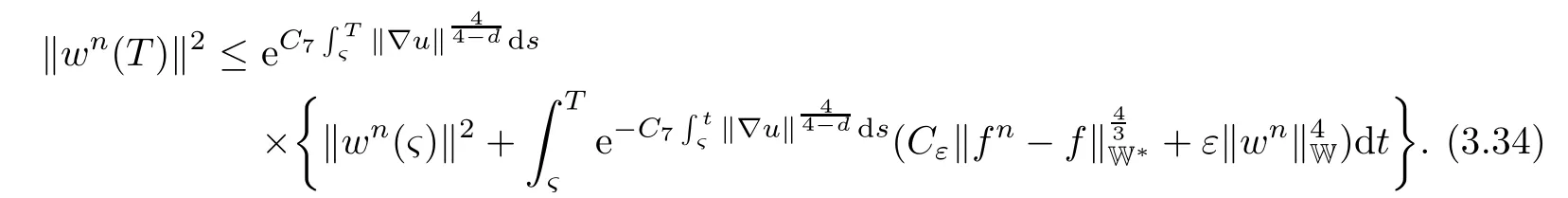

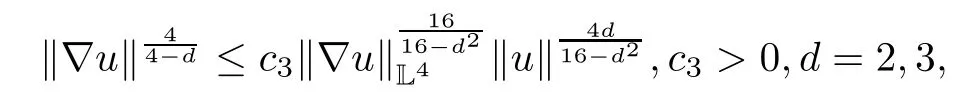
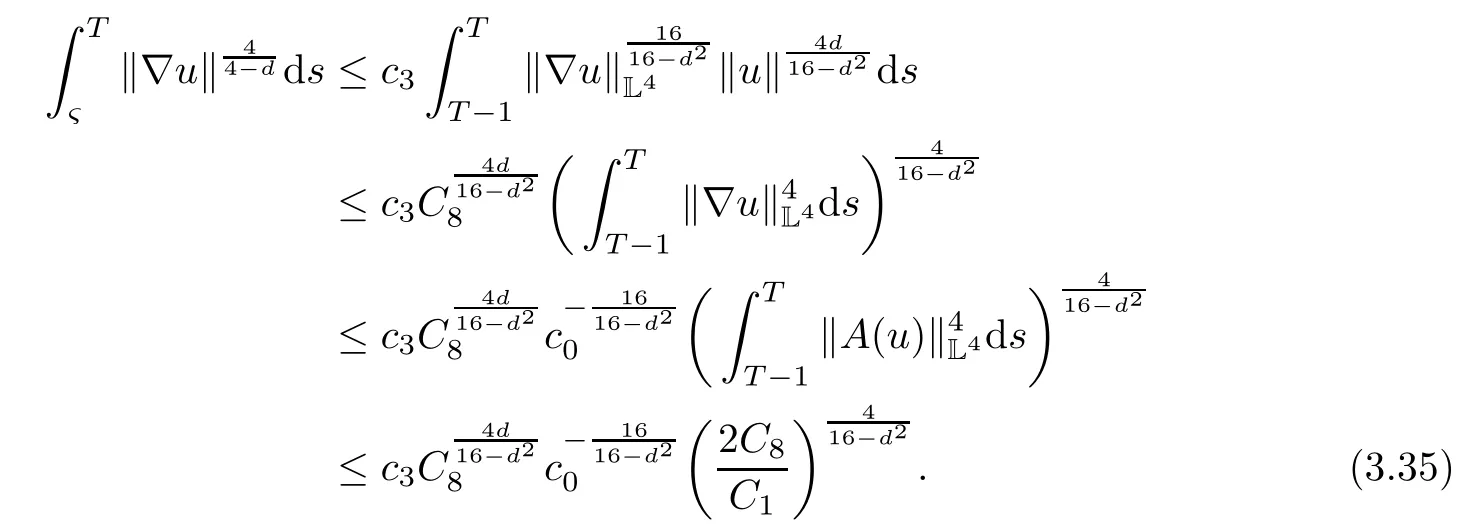
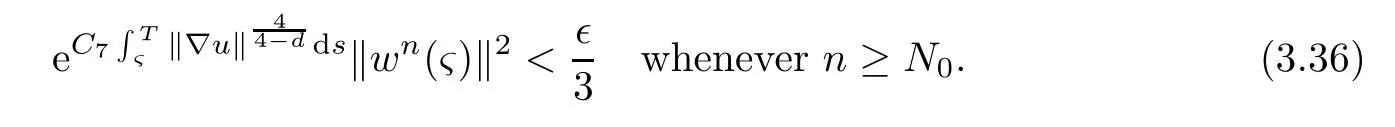
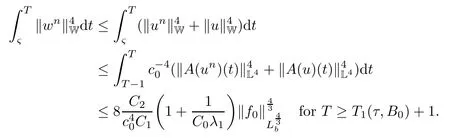
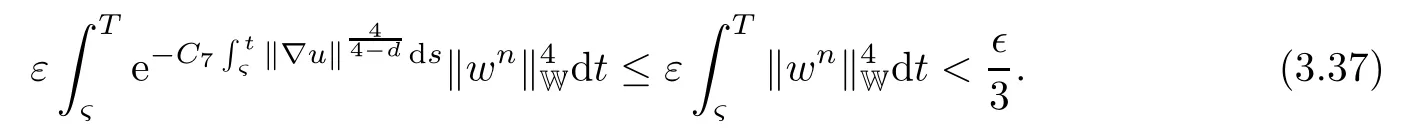
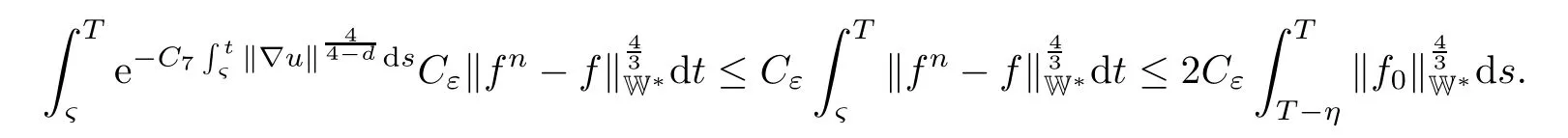
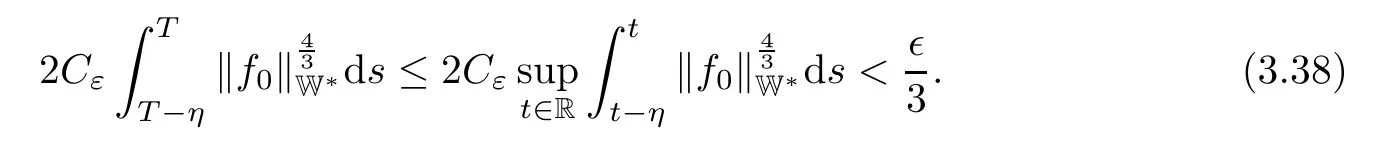
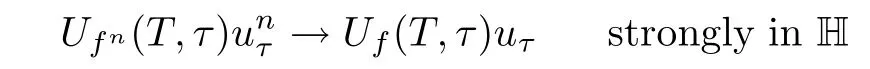
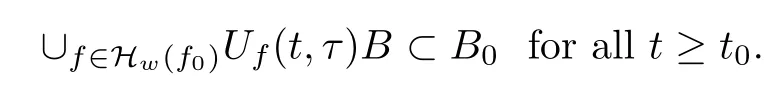
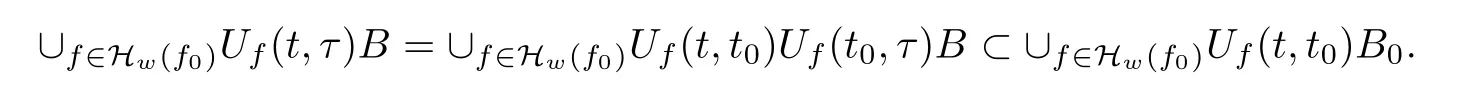
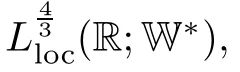
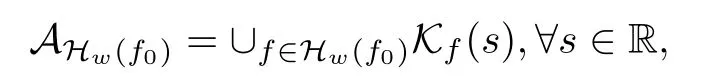
4 Convergence of the Solution and the Uniform Attractor
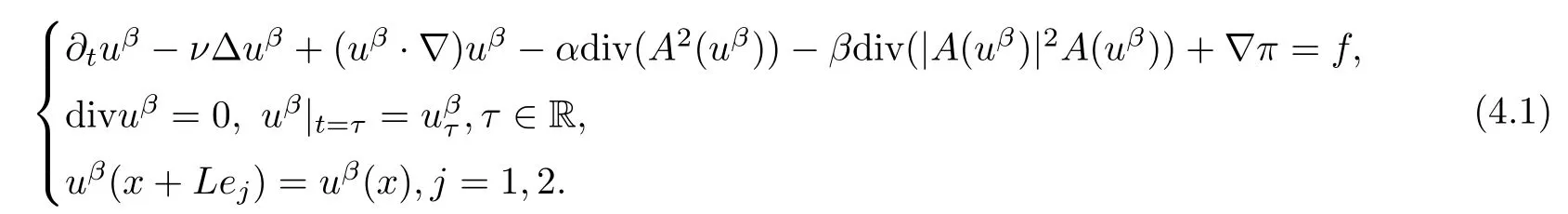

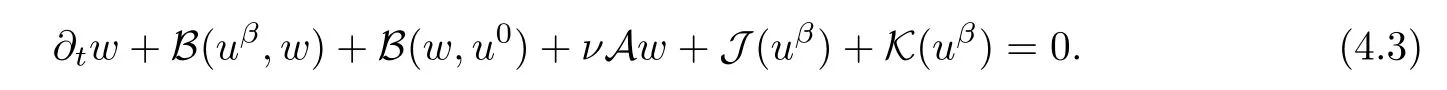
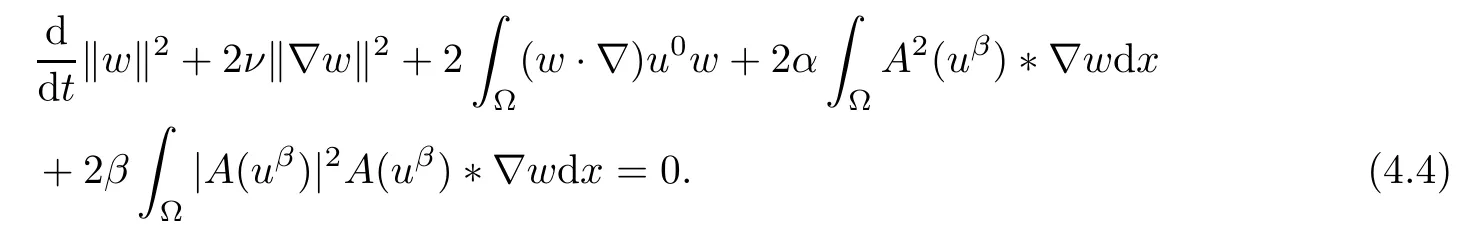
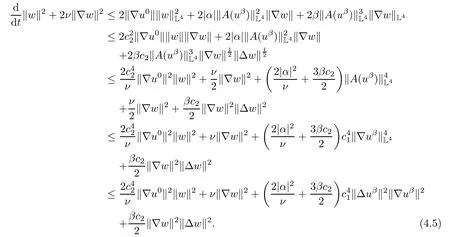
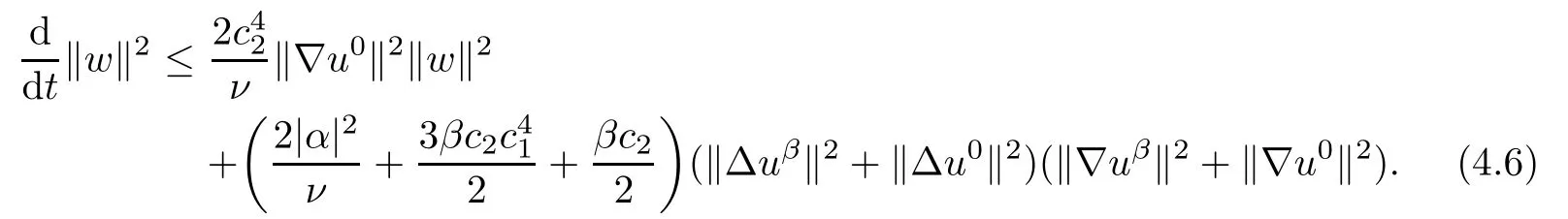
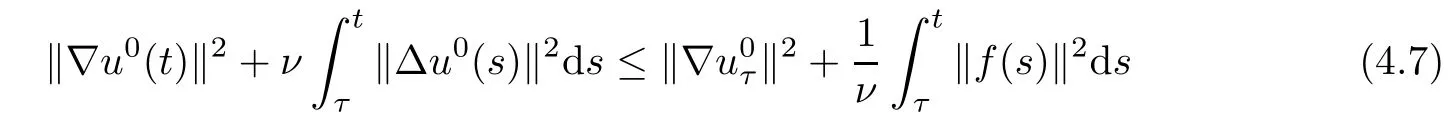
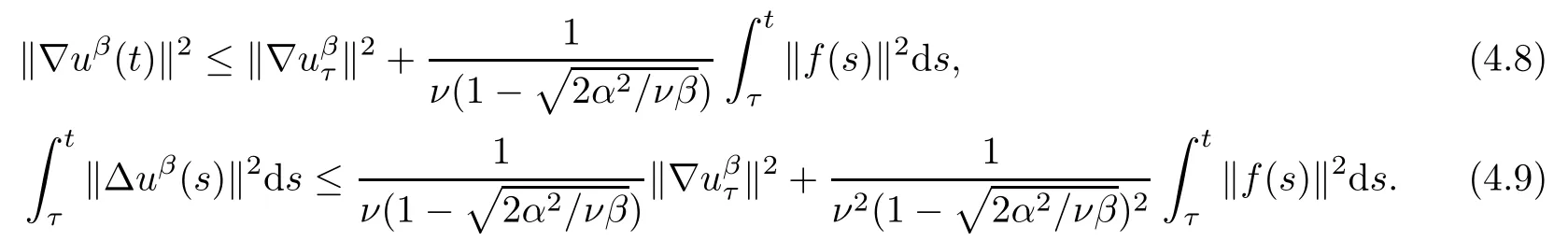
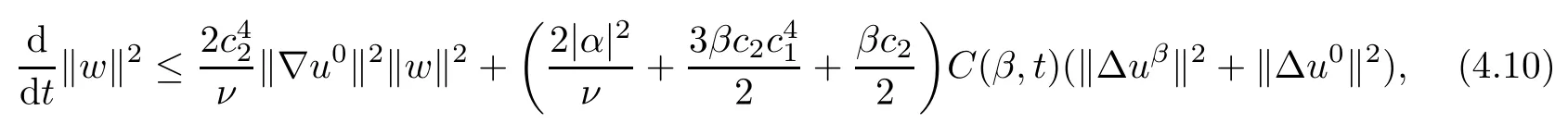
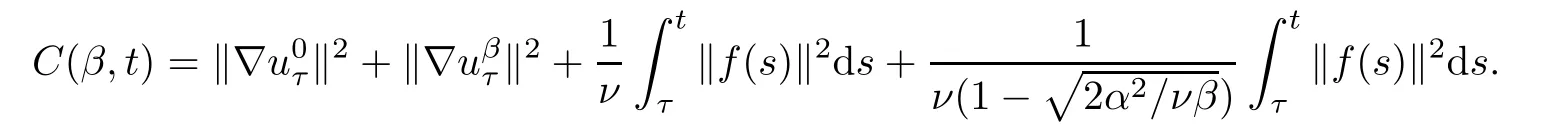
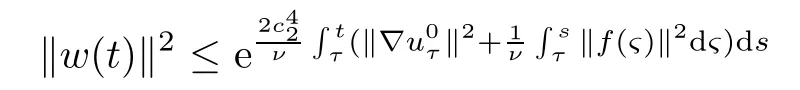

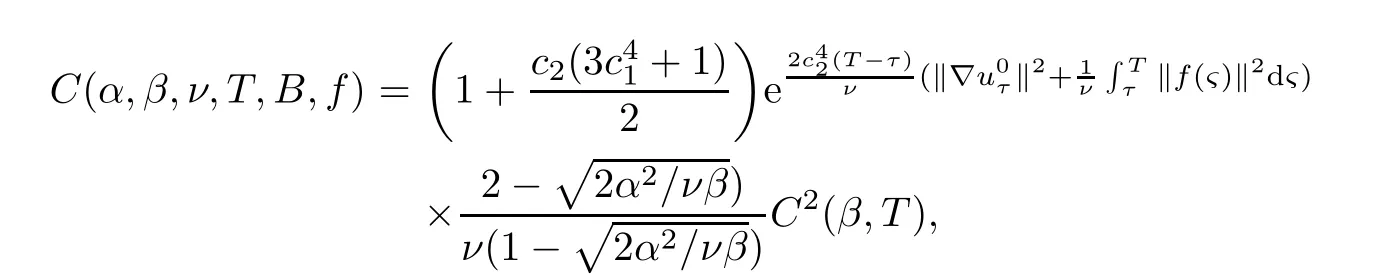
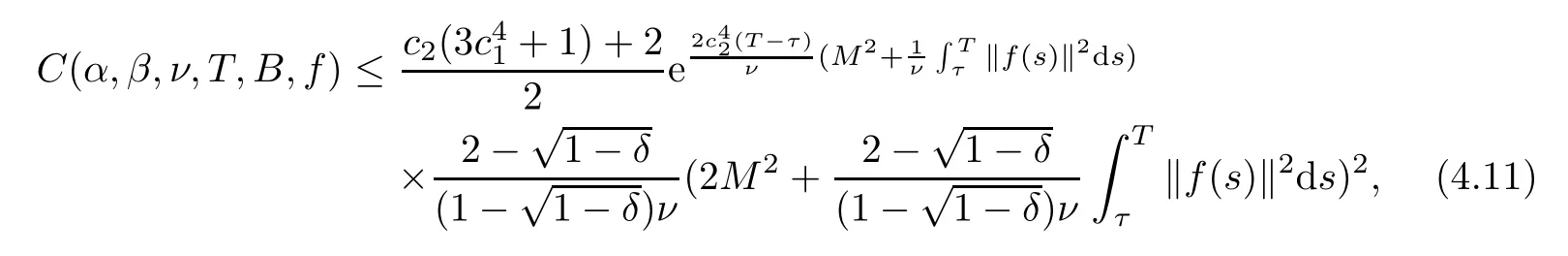
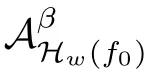
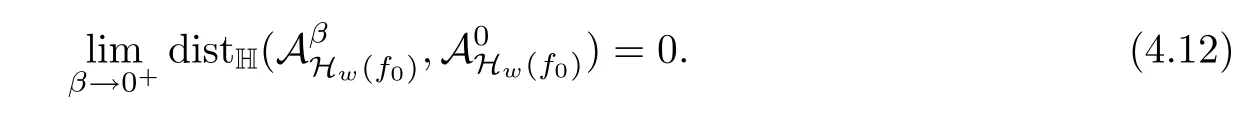
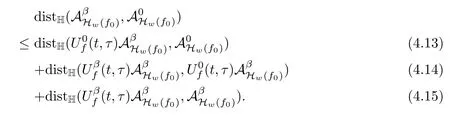
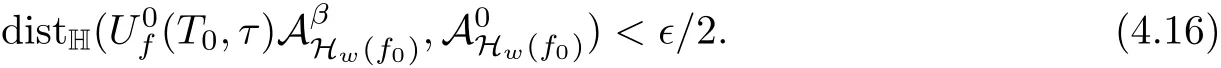
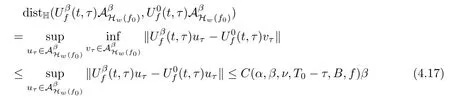
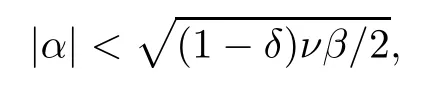
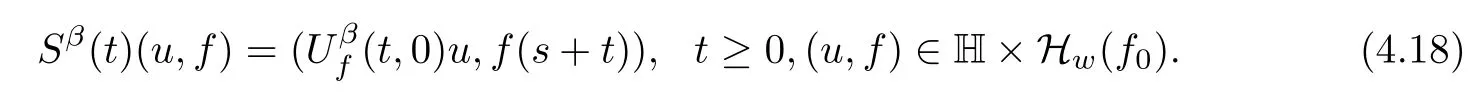
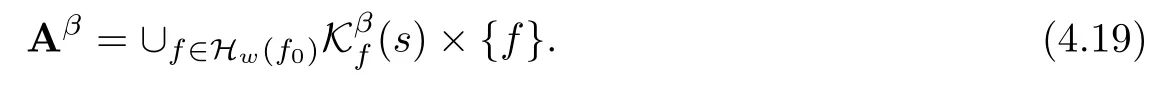
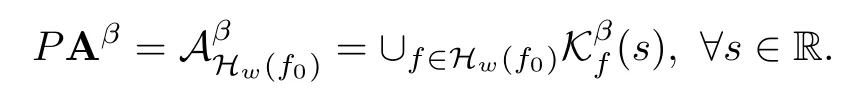
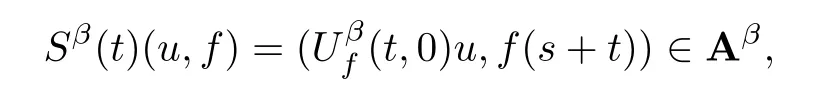
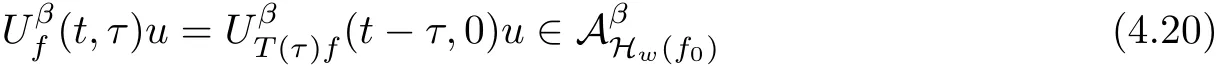
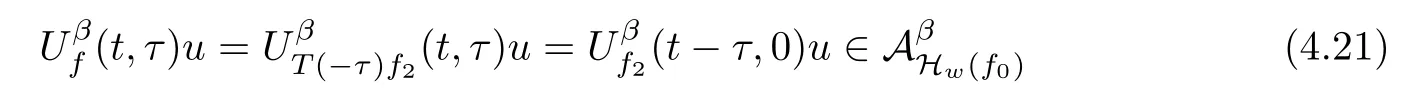
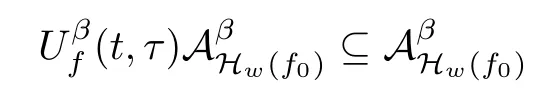
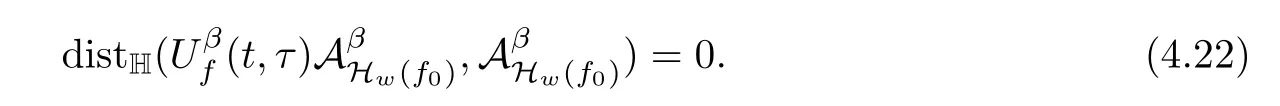
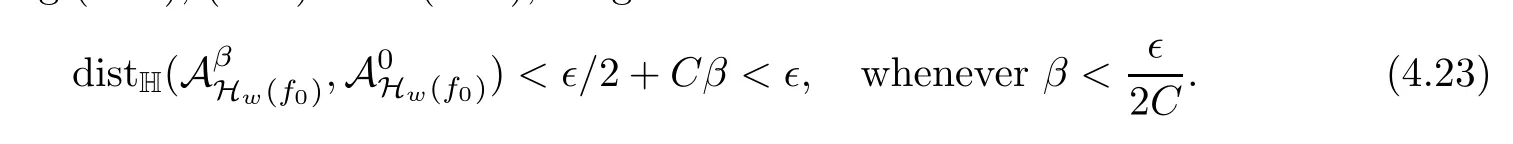
 Acta Mathematica Scientia(English Series)2016年6期
Acta Mathematica Scientia(English Series)2016年6期
