Zhi-yong Liang (梁志勇), Liang Wei (魏亮), Jing-yu Lu (盧錦煜), Xiao-hong Qin (覃小紅)

1. College of Science, Donghua University, Shanghai 201620, China, E-mail: zhyliang@dhu.edu.cn

2. Key Laboratory of Textile Science and Technology, Ministry Education, College of Textiles,

Donghua University, Shanghai 201620, China

Introduction

The micro-flapping wing aircraft is an aircraft based on the bionic principle, as the flying birds and insects. Compared with the fixed wing and rotary wing aircraft, the main features of the micro-flapping wing aircraft are that they are integrated systems that integrate the functions of lifting, hovering and propelling, they can complete a long-distance flight with a small amount of energy, and with a stronger mobility.A very small Reynolds number (about 101-104smaller)is involved, in which the viscosity effect of air increases greatly. In the boundary layer, the laminar flow separates, resulting in laminar separating bubbles and the aerodynamic characteristics are significantly different from those in a high Reynolds number situation[1]. The flight of flapping wings was studied extensively.

Zhang et al.[2]simulated the periodic motion of small insects by the dynamic hybrid grid technology and the unsteady method of incompressible flow based on the virtual compression technology. Bai et al.[3]simulated the hovering flight of a single flapping wing of fruit flies in three modes: the advanced mode,the symmetric mode and the delay mode, and combined with aerodynamic coefficients and flow structures, they analyzed the mechanism by which fruit flies obtain a high lift force in their hovering flight.Ohmiet et al.[4,5]studied the starting process of the vortex at a high attack angle with the wing?s pitching movement, including the forms of the vortex, and the factors that affect the formation of the vortex.Triantafyllou et al.[6]proved that the structure of the trailing vortex has a great influence on the formation of the propulsion. Nskata et al.[7]presented a new model of flapping-wing aerodynamics, called a CIQSM, based on a combination of the CFD data and the quasi-steady modelling. Tay et al.[8,9]used a numerical simulation method to investigate the validation of the immersed boundary method and the flapping micro-aerial vehicle. The aerodynamic performance of the flexible flapping wing was investigated through numerical simulations based on the fluid-structure coupling method[10]. Banazadeh and Taymourtash[11]presented the modeling and the simulation of open loop dynamics of a rigid body insect-like flapping wing. MH Dickson?s research indicates that the turning phase of insect’s wings will affect the direction of the first peak lift force and it?s emergence moment, and that the flapping wing flight has a unique advantage in using the trail flow to obtain a part of lift force, which leads to a conclusion that the flapping wing could absorb the energy of the trailing flow. Based on the insect wing study a twodimensional single flapping wing model is built, and the dynamic mesh technique and the UDF function are used to simulate the flight of a flapping wing in the advanced mode. The unsteady mechanism is studied and some useful conclusions are drawn.

1. The model

This paper takes the NACA0012 wing as the two-dimensional simplified wing section, and studiesthe flapping motion in the state of the hovering flight. The controlling parameters for the wing moving up and down are set symmetrically, and the axis of rotation is set a quarter chord length from the leading edge. The following functions in the model are adopted to describe the translation and the rotationof the hovering flapping movement. Thevelocity is expressed as:

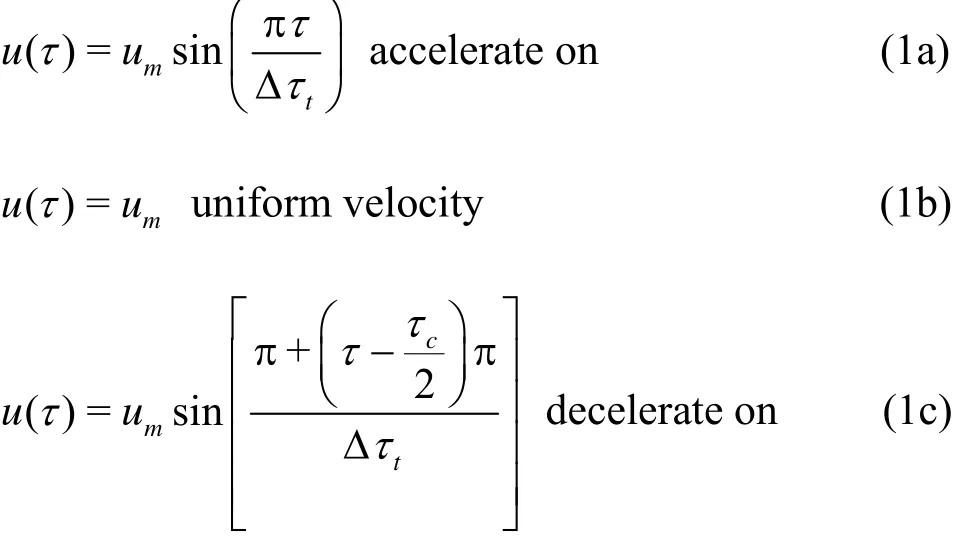
where τ is the time,mu is the maximum speed of the translational motion,tτΔ is the total time of the translational motion, andcτ is the flapping cycle.

The angular velocity function[12]of the rotation motion is expressed as

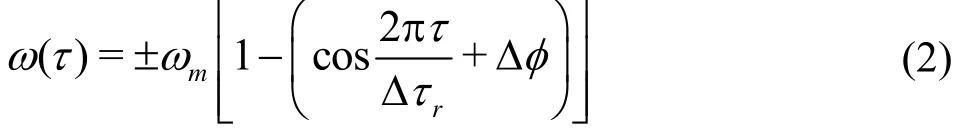
wheremω is the maximum angular velocity,rτΔ is the total time of the pitching rotation, and φΔ is the phase difference of the rotation and the translation.

Some main physical parameters are:

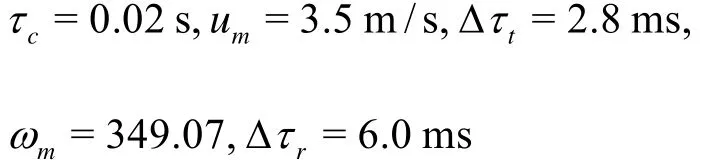
The attack angle iso30, the rotation angle is 120o, and the leading phase is 8.0%. The calculation area is a rectangle of 0.16 m×0.06 m, and the chord length of the wing NACA0012 is c = 0.01m. The four edges of the calculation field are static wall boundaries, and the boundary of the wing is the dynamic wall boundary. The triangular unstructured grids are used in this model. The total number of the grids is 4.67×104. The movement of the flapping wing has a high speed, it behaves as in the turbulence model. The smooth spring model and the local reforming model are used to produce the dynamic grids.

2. The results and discussions

2.1 Lift and drag coefficients

Figure 1 shows the lift and drag coefficients in a cycle, the vertical axis is the lift or drag coefficients,and the abscissa is the time, covering the range of 0-1.As shown in the Fig.1(a), the lift coefficient changes slowly in the intermediate stage, and there are two areas in which the lift coefficient changes dramatically.In the range of -0.05-0.02, the lift coefficient reduces rapidly and then has a rapid increase in the other direction and the lowest value of the lift coefficient increases to 2.23 quickly. In this stage the attack angle becomes an obtuse angle due to the fact that the flapping wing turns in the advance phase. In the end of the turning phase, the flapping wing turns into the other phase, in which the wing keeps a same attack angle flapping and the lift coefficient decreases rapidly from the first peak 2.23 to 0.07, and then it turns into the translation motion, in which the attack angle and the velocity keep unchanged, the lift coefficient turns into the rising and stable stages. In the range of 0.25-0.38, the lift coefficient comes into its second rising stage and it reaches the peak value. In this rising stage, the flapping wing keeps in a same attitude of pitching nose-up. After that, the wing turns into the position of its stalling angle, so that the lift coefficient decreases rapidly to negative values.Figure 1(b) shows that the drag coefficient behaves quite differently when flapping up and down. When in the range of 0-0.05, the drag coefficient is positive,there are two peaks, and also the velocity increases rapidly. In this stage, the flapping wing keeps in an attitude of pitching nose-up. While in the range of 0.50-0.10 the drag coefficient is negative and also sees two valley values.

2.2 The vortex distribution of the flapping wing

Fig.1 The lift and drag coefficients in a cycle

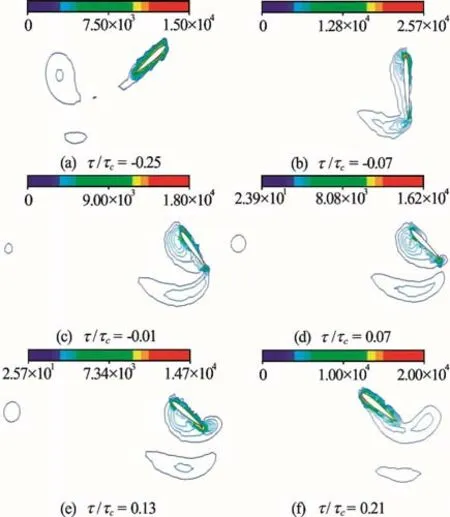
Fig.2 (Color online) The vortex distributions at different times

Figure 2 shows the vortex distribution at different times. The interaction between the vortex and the flapping wing is a significant factor of the high lift coefficient. With a proper angle of the flapping wing,a high lift force can be achieved. As shown in the pictures, in the stage of a uniform velocity (Fig.2(a)), the horizontal angle of attack remains a constant and there is a continuous vortex shedding from the wake flow.At the same time, the backflow area of the front edge constantly strengthens and finally, a strong front vortex is formed. And the vortex attached at the front edge provides a certain lift force for the wing, makes a gentle change of the lift coefficient in this phase. And then, the wing pulls up with a constant or rapid speed(Figs.2(a), 2(b)), the vortex of the trailing edge breaks away from the wing and a rotating vortex is formed,acting on the wing. Along with the continuous enhancement of the leading edge vortex, the lift coefficient of the flapping wing reaches the high peak. Then the wing enters into a deceleration phase (Figs.2(b), 2(c)).At about τ / τc= -0 .07, the states on the top and the bottom of the wing alternate each other, the vortex of the trailing edge accumulates on the direction of the forward motion and interacts with the wing, to form the trailing edge vortex at this time and the previous turning vortex cannot alternate each other, with a continuous decline of the lift coefficient. In the next stage, the wing accelerates in the other direction(Figs.2(e), 2(g)), the latter trailing edge vortex and the previous turning vortex which sheds from the trailing edge can alternate each other. And since the two vortexes are opposite in their circling directions, so they can produce a strong vortex to raise the lift coefficient again.

2.3 The pressure distribution of the flapping wing

Figure 3 clearly demonstrates the pressure distribution around the wing. In the translational stage(Fig.3(a)), there are two pressure centers, respectively located in the front and the back of the trailing edge.The forward total pressure obviously is higher than the other, which steadies the lift coefficient in the stage. In the initial stage (Figs.3(a), 3(b)), the wing begins to overturn, the low-pressure center near the wing is destroyed. Since the angular velocity increases,the volume of the bottom wing increases suddenly, the air becomes thin and the intensity of the pressure reduces, which leads to a stable low pressure area.Oppositely a high-pressure zone appears on the top.Due to the pressure difference, the lift coefficient increases at this stage. As the wing goes into the early deceleration phase (Figs.3(b), 3(c)), due to the fact that the states on the top and the bottom alternate,together with the fact that the original high pressure area under the wing gradually sheds to the wake flow.A low pressure center forms on the upper area of the original leading edge, which makes the pressure difference decrease and results in the falling of the lift coefficient. Then the wing goes into the later deceleration stage. Because the original high pressure area under the plane turns into the low pressure area and the shedding high pressure area is attached at the trailing edge of the original upper plane, the pressure difference increases again, this makes the lift coefficient rise again. The different angles and speeds of the movement can lead to different pressure distributions,pressure center behind the wing (Fig.3(a)), keeping two pressure centers in the following phase of equal attack angle.

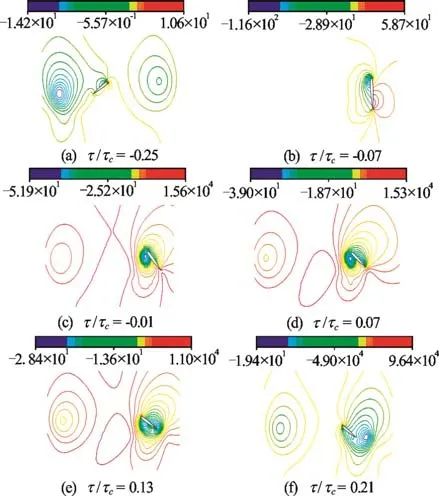
Fig.3 (Color online) The pressure distributions at different times

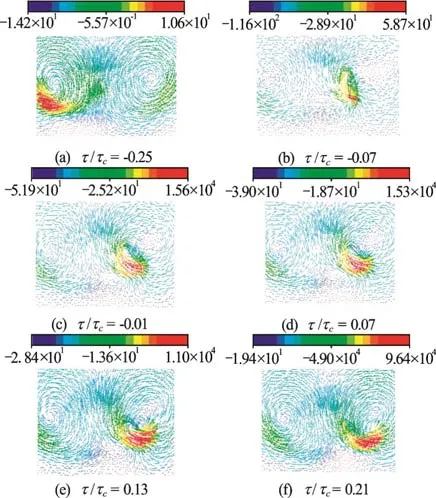
Fig.4 (Color online) The velocity vector distributions at different times

2.4 The Velocity vector distribution of the flapping wing

From the velocity distribution, we can clearly see the velocity distribution around the wing. As shown in Fig.4, two annular flows appear, respectively, on the front and behind areas of the flapping wing. The two centers are on a horizontal line and the flapping wing moves back and forth between the two centers.Because of the influence of the two airstream, the vortex constantly sheds from the trailing edge. In the process of a uniform motion, the speed of the airstream away from the wing is greater than the other,while the overturn of the wing just makes the two airstream change their speeds. In the whole process the wing always maintains to have two annular flow centers. When the wing approaches one of them the annular flow center is destroyed (Figs.4(b)-4(e)), but then it will be replaced immediately by the rotational center of the wing.

3. Conclusions

In this paper the flapping wing is simulated numerically in the advanced mode, and the high lift mechanism of the flapping wing is studied from the following aspects: the lift and drag coefficients, the vortex distribution, the pressure distribution, and the velocity vector distribution. Based on this study some conclusions are drawn. The interaction between the leading edge vortex and the trailing edge vortex is an important factor regarding the high lift coefficient,and this conclusion is consistent with the Refs.[13-20].In different stages the flapping wing needs a proper attack angle to obtain a high lift force. Before and after the uniform-motion stage of the flapping wing,two pressure centers appear and the low pressure center falls off later. In the whole movement process,there always exist two annular airstream centers and they change their speeds alternatively.

in different stages of time, the movement style of the flapping wing is variable. In the following stage, the wing speeds up in the other direction, with the low pressure area shedding from the leading edge of the bottom plane, the high pressure area is pushed out from the trailing edge and the pressure difference reduces again, with the falling of the lift coefficient.The detached low pressure area forms, with a low

[1] Zaitsev A. A., Sharina L. V. Aerodynamic calculation of normal hovering flight [J]. Fluid Dynamics, 1983, 18(4):554-560.

[2] Zhang L. P., Chang X. H., Duan X. P. et al.Numerical simulations of the “clap-fling” motion for tiny insect wings [J]. Acta Aerodynamica Sinica, 2009, 27(2):246-254.

[3] Bai P., Cuie J., Li F. et al. Study of high aerodynamic lift mechanics of hovering insect flapping wing at low Reynolds number [J]. Acta Aerodynamica Sinica, 2007,25(2): 175-182.

[4] Ohmi K., Coutanceau M., Loc T. P. et al.Vortex formation around an oscillating and translating airfoil at large incidences [J]. Journal of Fluid Mechanics, 1990, 211:37-60.

[5] Ohmi K., Coutanceau M., Daube O. et al. Further experiments on vortex formation around an oscillating and translating airfoil at large incidences [J]. Journal of Fluid Mechanics, 1991, 225: 607-630.

[6] Triantafyllou M. S., Triantafyllou G. S., Gopalkrishnan R.Wake mechanics for thrust generation in oscillating foils[J]. Physics of Fluids A-Fluid Dynamics, 1991, 3(12):2835-2837.

[7] Nakata T., Liu H., Bomphrey R. J. A CFD-informed quasi-steady model of flapping-wing aerodynamics [J].Journal of Fluid Mechanics, 2015, 783: 323-343.

[8] Tay W. B., DENG S., Van Oudheusden B. W. et al.Validation of immersed boundary method for the numerical simulation of flapping wing flight [J]. Computers and Fluids, 2015, 115: 226-242.

[9] Tay W. B.,Van Oudheusden B. W., Bijl H. Numerical simulation of a flapping four-wing micro-aerial vehicle [J].Journal of Fluids and Structures, 2015, 55: 237-261.

[10] Yang W., Wang L., Xue D. et al. Aerodynamic performance of micro flexible flapping wing by numerical simulation [J]. Procedia Engineering, 2015, 99(1): 1506-1513.

[11] Banazadeh A., Taymourtash N. Nonlinear dynamic modeling and simulation of an insect-like flapping wing [J].Applied Mechanics and Materials, 2014, 555: 3-10.

[12] Zhao P. F., Liu C. Y., Zhu L. W. et al. Visualization of vortex field of 2-D flapping wing motion [J]. Journal of University of Science and Technology of China, 2005,35(4): 441-447.

[13] Liu H., Ellington C. P., Kawachi K. et al. A computational fluid dynamic study of hawkmoth hovering [J].Journal of Experimental Biology, 1998, 201(4): 461-477.

[14] Lan S. L., Sun M. Aerodynamic properties of a wing performing unsteady rotational motions [J]. Acta Mechanica Sinica, 2001, 33(2): 173-182.

[15] Lu K., Xie Y. H., Zhang D. et al. Numerical investigations into the asymmetric effects on the aerodynamic response of a pitching airfoil [J]. Journal of Fluids and Structures,2013, 39(5): 76-86.

[16] Zhou C. H., Lin Y. F. Numerical study on aerodynamic performance of flapping wings [J]. Journal of Harbin Institute of Technology, 2006, 38(9): 1403-1405.

[17] Zhang L., Shang J. H., Zhang Z. Y. et al. Tidal current energy update 2015-Hydrodynamics [J]. Journal of Hydroelectric Engineering, 2016, 35(2): 1-15(in Chinese).

[18] Lin J., Lin B. L., Sun J. et al. Modelling hydrodynamic processes in tidal stream energy extraction [J]. Journal of Hydrodynamics, 2016, 28(6): 1-11.

[19] Wang S. Q., Sun K., Zhang J. H. et al. The effects of roll motion of the floating platform on hydrodynamics performance of horizontal-axis tidal current turbine [J]. Journal of Marine Science and Technology, 2015, 74(C): 1058-1064.

[20] Zhang L., Wang S. Q., Sheng Q. H. et al. The effects of surge motion of the floating platform on hydrodynamics performance of horizontal-axis tidal current turbine[J]. Journal of Marine Science and Technology, 2015,74(C): 796-802.