CRE Solvability,Nonlocal Symmetry and Exact Interaction Solutions of the Fifth-Order Modi fied Korteweg-de Vries Equation?
Wen-Guang Cheng(程文廣), De-Qin Qiu(邱德勤),and Bo Yu(余波)
1 Introduction
Over the last few decades,constructing exact solutions for nonlinear evolution equations(NLEEs)have become an attractive topic in nonlinear science.Up to now,many effective approaches have been established to obtain exact solutions of NLEEs.Some of them are respectively the inverse scattering transformation,[1]the Darboux and B?cklund transformations,[2?3]Hirota’s bilinear method,[4]Painlev′e analysis,[5]symmetry reductions,[6]the homogeneous balance method,[7]the tanh method[8]and the separated variable method,[9]and so on.However,these methods are insufficient to find interaction solutions among different nonlinear excitations.
Recently,it is found that the residue of truncated Painlev′e expansion with respect to the singular manifold is just the nonlocal symmetry,which is called residual symmetry.[10?11]According to the novel results of the symmetry reduction with nonlocal symmetries,Lou[12]further proposed the consistent Riccati expansion(CRE)method.The CRE method can be used to identify CRE solvable systems and it is a more direct but much simpler method to find interaction solutions between a soliton and other nonlinear waves,such as the soliton-cnoidal waves,soliton-perodic waves,soliton-error function waves,and soliton-rational waves.[12?22]
In this paper,we would like to consider the following fifth-order modi fied Korteweg-de Vries(fmKdV)equation
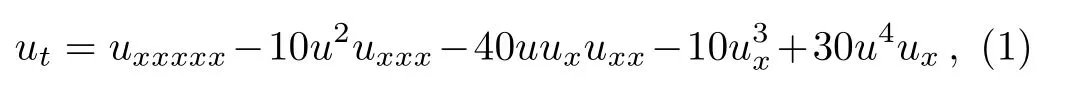
which possesses a close connection with the known fifthorder KdV equation
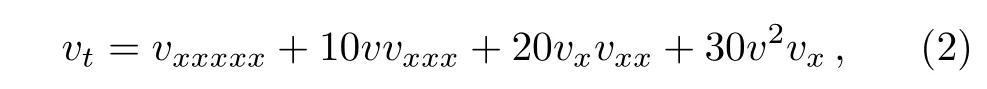
by the Miura transformation

that will convert Eq.(2)to Eq.(1).It is well known that the known fifth-order KdV equation has wide application in Physics,so the study of Eq.(1)is being of potential application in Physics besides the academic interest.The fmKdV equation(1)is a higher-order equation of the mKdV hierarchy,the Lax pair and bi-Hamiltonian structure were studied in Ref.[23].In Ref.[24],a semidiscrete version for the fmKdV equation(1)was constructed from the three known semidiscrete mKdV fluxes.Kwak[25]proved the local well-posedness of the fmKdV equation(1)for low regularity Sobolev initial data via the energy method.
The paper is organised as follows.In Sec.2,the CRE method is applied to prove the fmKdV equation is CRE solvable.In Sec.3,starting from the last consistent differential equation,three special form of interaction solutions between the soliton and the cnoidal periodic wave of this equation are presented both analytically and graphically.In Sec.4,the nonlocal symmetry related to the CTE and the nonlocal residual symmetry of the fmKdV equation are obtained.Also,the relationship between them is given.Then the corresponding finite transformation group is obtained by the localization of residual symmetry to the Lie point symmetry.The last section is a summary and discussion.
2 CRE Solvability and CTE Solvability
2.1 CRE Solvability
In this section we apply the CRE method in Ref.[21]to Eq.(1).According to the leading order analysis,the solutionuis selected as the following ansatz(R≡R(w))
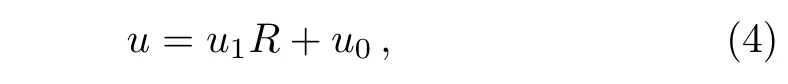
whereu0,u1,andware functions of(x,t),andRis a solution of the Riccati equation
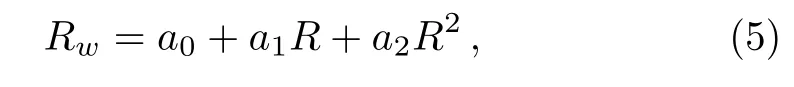
which admits a solution tanh(w).
Substituting Eq.(4)with Eq.(5)into Eq.(1)and vanishing all the coefficients ofRifor alli,we obtain seven overdetermined differential equations with only three undetermined functions.It is fortunate that these overdetermined equations are consistent.As a result,we have
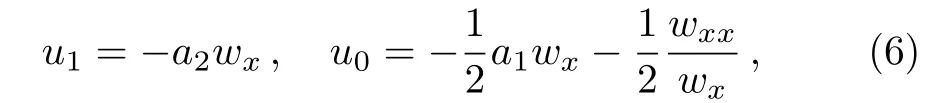
and the functionwsatisfies a generalization of the Schwarzian form of Eq.(1)
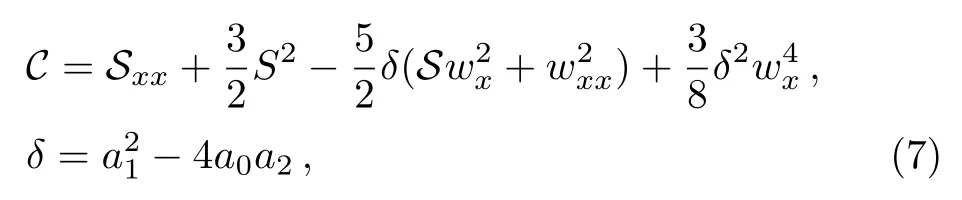
where the notationsCandSare defined as
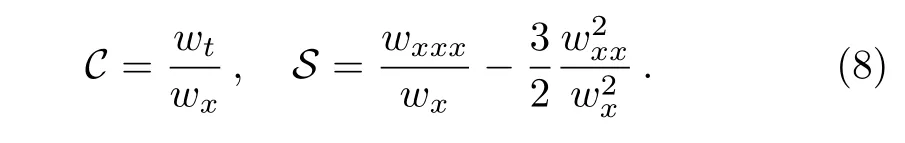
From the definition in Ref.[12],we deduce that the fmKdV equation is CRE solvable.
2.2 CTE Solvability
We consider a special solution of the Riccati equation(5)as follows

the truncated expansion expression(4)is converted to
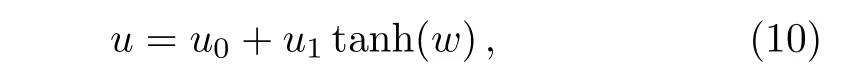
whereu0,u1,andware determined by Eqs.(6)and(7)witha0=1,a1=0,a2= ?1,andδ=4.Hence,we obtain
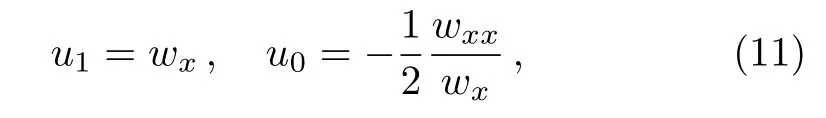
andwneeds to satisfy
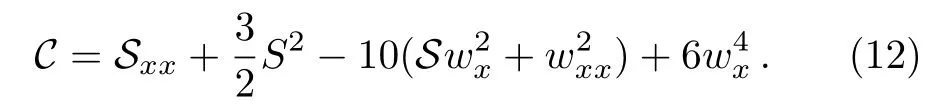
From above,it shows that the fmKdV equation is consistent tanh expansion(CTE)solvable.It is obvious that a CRE solvable system must be consistent tanh expansion(CTE)solvable,and vice versa.
In summary,we can establish the following nonauto-BT theorem for Eq.(1).
Theorem 1Ifwis a solution of Eq.(12),then,
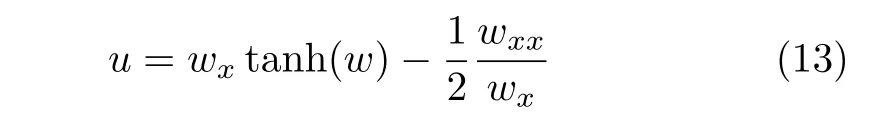
is a solution of the fmKdV equation(1).
3 Exact Solutions from Theorem 1
By means of Theorem 1,we can derive some exact solutions of the fmKdV equation(1),in particularly the interaction solutions between one soliton and other kinds of complicated waves.Next,some special types of solutions are given.
3.1 Soliton Solution
A quite trivial straight line solution forwhas the form
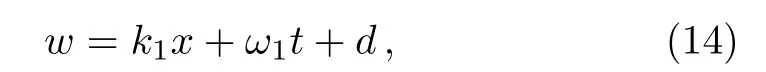
wherek1anddare the free constants,andω1is determined by the dispersion relation

Substituting Eq.(14)into the CTE result(13)leads to one kink soliton solution
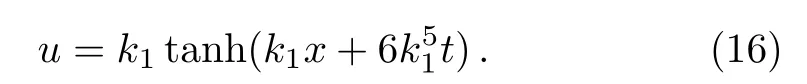
3.2 Soliton-Cnoidal Wave Interaction Solutions
To find out the soliton-cnoidal wave interaction solutions,we assumewin the form

Substituting Eq.(17)into Eq.(12),we can find thatW1satis fies
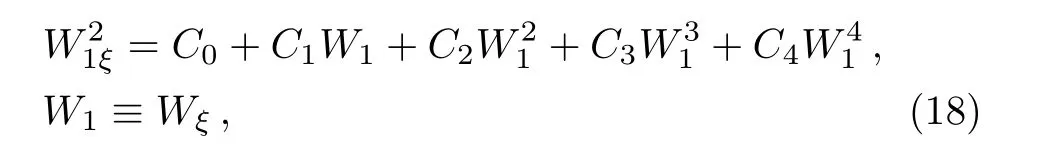
with
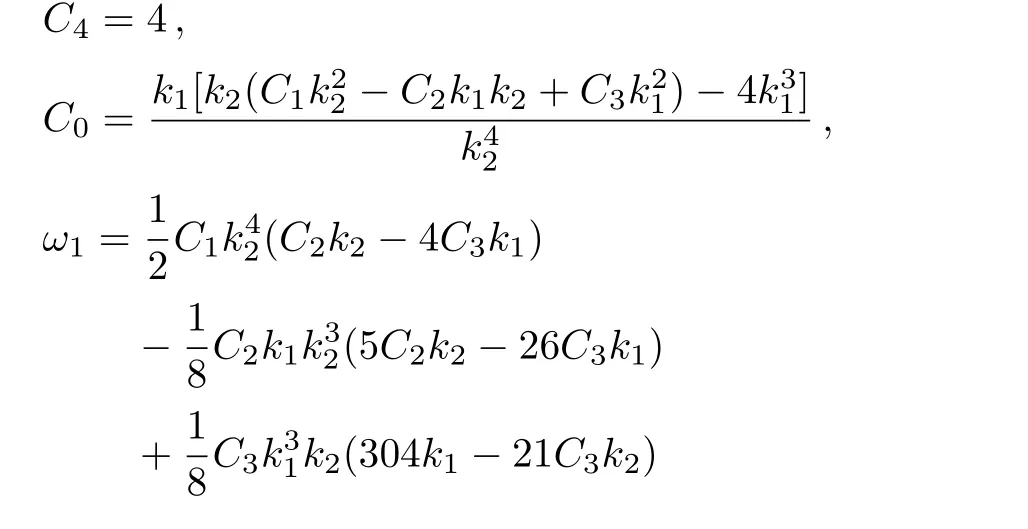
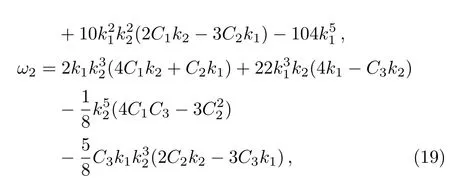
while all the other constants remain free.Then the explicit solution of the fmKdV equation writes as
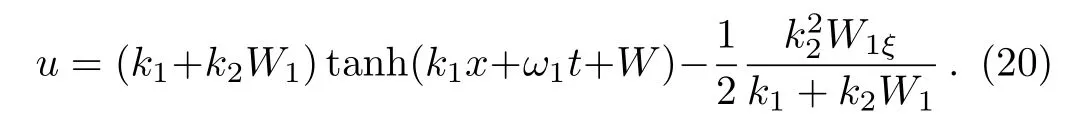
It is known that the solutions of Eq.(18)can be expressed in terms of Jacobi elliptic functions.Thus,the solution(20)reveals the interactions between one soliton and cnoidal periodic waves.In the following we will list three nontrivial cases to obtain this kind of solution.
Case 1The first simple solution of Eq.(18)is given by

Substituting Eqs.(19)and(21)into Eq.(18)yields
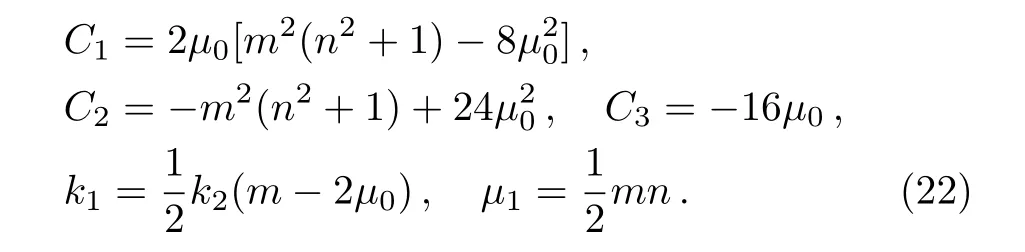
Then the exact soliton-cnoidal wave interaction solution can be derived as
where{k2,m,n,λ}are arbitrary constants,ξ=(1/8)k2[8x+m4(3n4+2n2+43)t].Hereafter,S,CandDare the usual Jacobian elliptic functions sn,cn and dn with modulusn,respectively.
Figure 1 plots one kink soliton in the cnoidal periodic wave background expressed by Eq.(23),and the parameters are fixed at
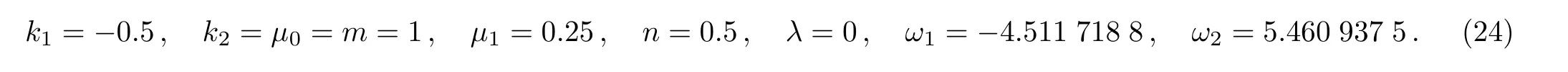
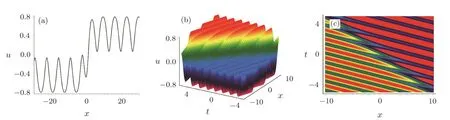
Fig.1 The first special form of soliton-cnoidal wave interaction solution of u expressed by Eq.(23)with the parameters being fixed at Eq.(24).(a)The soliton-cnoidal wave structure at t=0;(b)The evolution of the soliton-cnoidal wave structure;(c)The density plot for the soliton-cnoidal wave structure.
Case 2As the second example,we consider the solution of Eq.(18)as

which leads to the soliton-cnoidal wave interaction solution of Eq.(1):
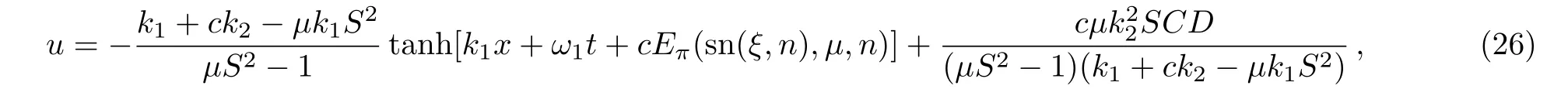
where{k2,μ,n}are three independent constants,Eπ(ζ,μ,n)is the third type of incomplete elliptic integral,and
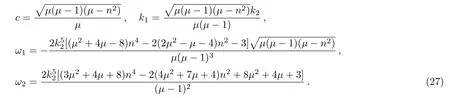
Figure 2 shows the structure of the soliton-cnoidal wave interaction solution(26)with the parameters chosen ask2=μ=0.5 andn=1.3.
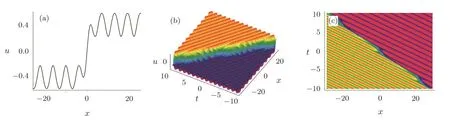
Fig.2 The second special form of soliton-cnoidal wave interaction solution of u generated by Eq.(26)with the parameters chosen as k2=μ=0.5 and n=1.3.(a)The soliton-cnoidal wave structure at t=0;(b)The dynamical evolution of the soliton-cnoidal wave;(c)The density plot for time evolution.
Case 3The third special solution of Eq.(18)is taken as the form

in this case,the interaction solution for Eq.(1)is obtained as:
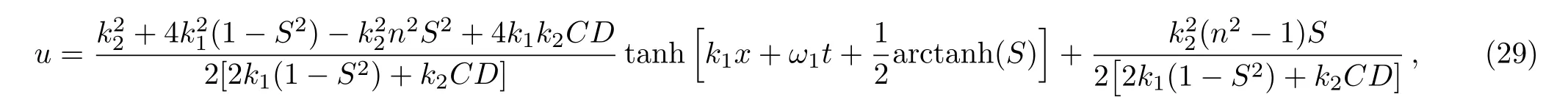
wherek1andnare two arbitrary constants,and
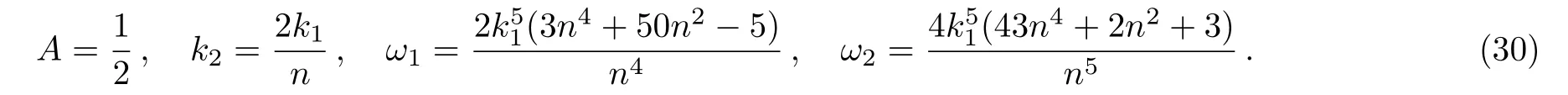
Figure 3 displays the third special form of soliton-cnoidal wave interaction solution for the fieldugiven by Eq.(29)with the parameters determined ask1=0.6 andn=1.5.
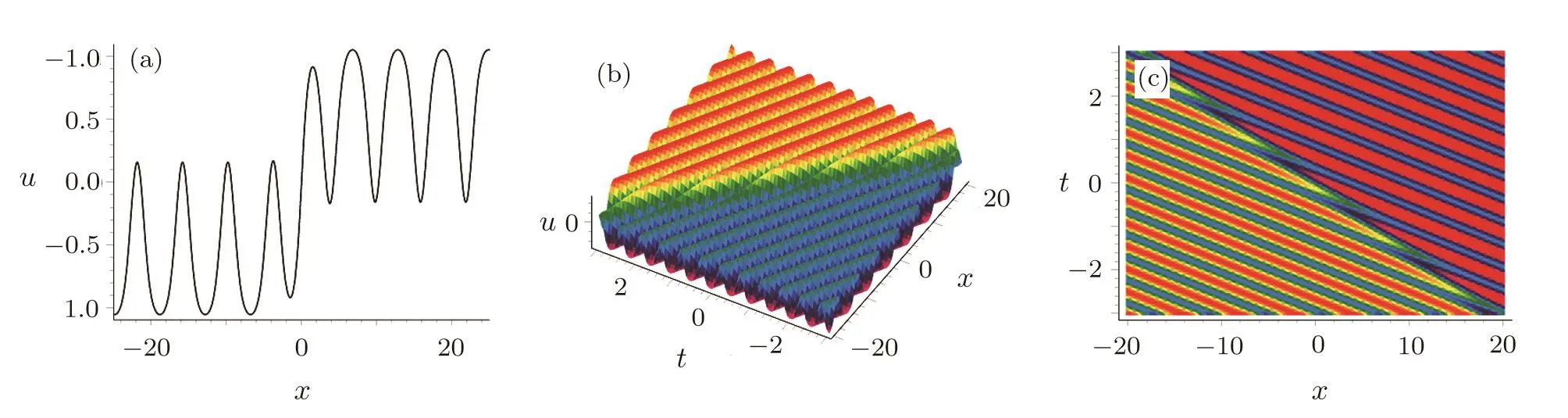
Fig.3 The third special form of soliton-cnoidal wave interaction solution of u given by Eq.(29)with the parameters determined as k1=0.6 and n=1.5.(a)One-dimensional image at t=0;(b)The corresponding three-dimensional view;(c)The density plot for soliton-cnoidal wave u.
In the ocean,there are some typical nonlinear waves such as soliton-cnoidal periodic wave.The interaction solutions may be useful for describing many more interesting physical phenomena,such as the Fermionic quantum plasma.[26]
4 Nonlocal Symmetry and Its Localization
4.1 Nonlocal Symmetry
Symmetries,including nonlocal symmetries,play an important role in nonlinear mathematical physics.In this subsection,the nonlocal symmetries of the fmKdV equation(1)will be studied.To seek the nonlocal symmetry related to the CTE,a nonauto-BT theorem for the fmKdV equation(1)is given as
Theorem 2Ifwis a solution to Eq.(12),then the fmKdV equation(1)has a solution
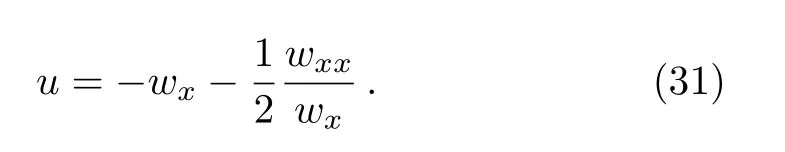
ProofBy direct calculation for substituting Eq.(31)into the fmKdV equation(1)by using thewequation(12).□
It is known that a symmetryσuof the fmKdV equa-tion(1)is defined as a solution of its linearized equation
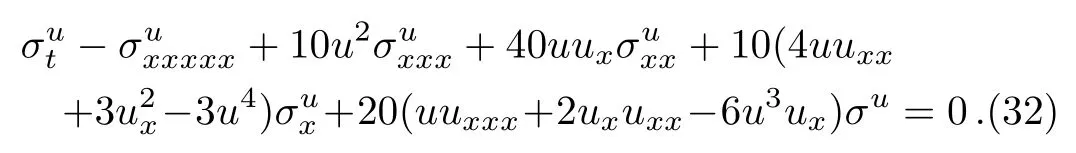
That means Eq.(1)is form invariant under the in finitesimal transformation
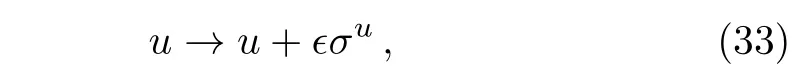
with?being an infinitesimal parameter.
Proposition 1The fmKdV equation(1)possesses a nonlocal symmetry
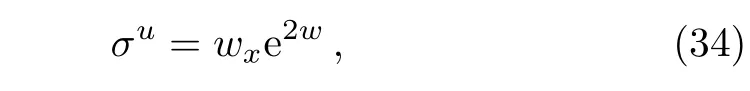
wherewsatisfies Eq.(12).
ProofBy direct calculation for substituting(34)into Eq.(32)by using the nonauto-BT(31)in Theorem 2 and thewEq.(12). □
Now,we make the following transformation
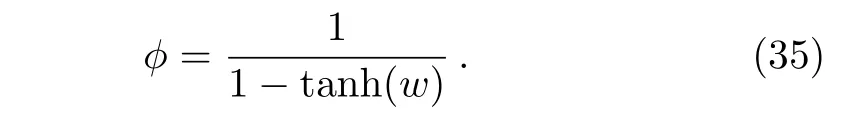
Substituting Eq.(35)into Eq.(34)leads to

which is the residual symmetry of Eq.(1).
Here we can derive the residual symmetry(36)from the truncated painlev′e expansion.For the fmKdV equation(1),we truncate the Laurent series as

where?=?(x,t)is the singular manifold,and functionsu0andu1are determined from the requirement for solutionuto satisfy Eq.(1).
Substituting Eq.(37)into Eq.(1)and comparing the coefficients of each powers of 1/?,we can simply find
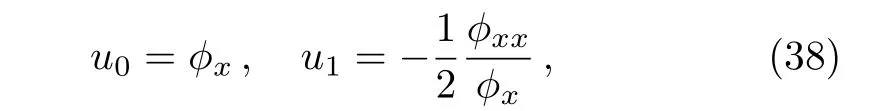
and the Schwarzian form of Eq.(1)
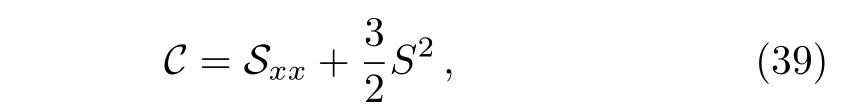
with the Schwarzian derivative
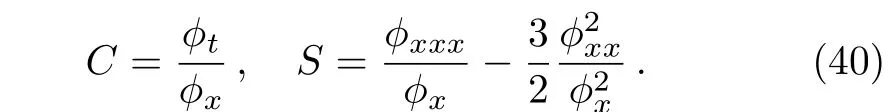
The Schwarzian form(39)is invariant under the M?bious transformation
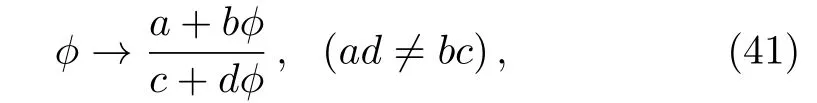
which means the function?possesses the Lie point symmetry in the form of
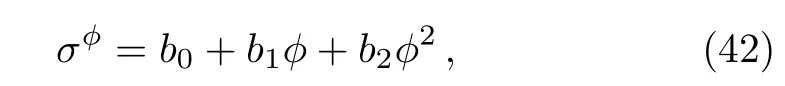
with arbitrary constantsb0,b1,andb2.From the above standard truncated Painlev′e expansion,we have the following nonauto-BT theorem.
Theorem 3If the field?is a solution of the Schwarzian equation(39),then

is a solution of the fmKdV equation(1).
ProofBy direct verification for substituting Eq.(43)into the fmKdV equation(1)with the help of the Schwarzian equation(39).
Based on the definition of residual symmetry,[10]Eq.(36)is the residual symmetry of Eq.(1).The residual symmetry(36)can be also obtained by using Schwarzian form(39)and nonauto-BT(43)in Theorem 3.[20,27?29]
It should be noted that the solution?of the Schwarzian equation(39)is just the spectral function related tou,therefore,Eq.(36)is also the spectral function symmetry of Eq.(1).It is straightforward to derive the Lax pair of Eq.(1)as follows:
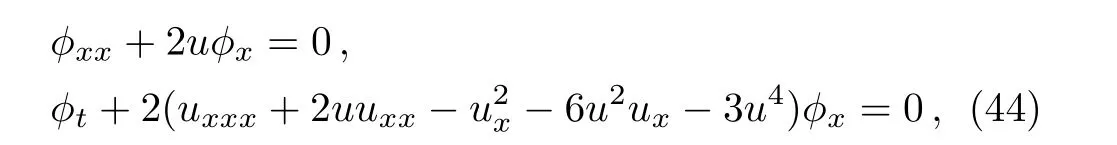
which is simpler than the result in Ref.[23].
4.2 Localization of Residual Symmetry
According to the Lie’s first theorem,the initial value problem related with the nonlocal residual symmetry(36)will be expressed as
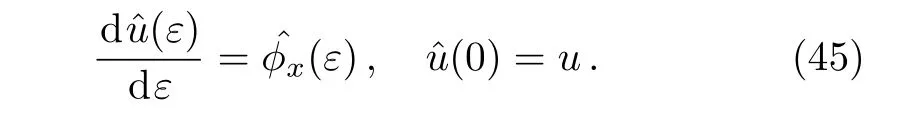
It is difficult to solve the initial value problem(45)due to the intrusion of the function??(ε)and its differentiation.[11]To eliminate the space derivative of the field?,the potential fieldfis defined as

Now the nonlocal residual symmetry of Eq.(1)is localized to a Lie point symmetry
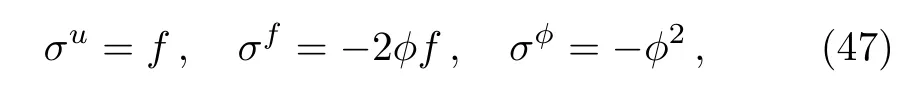
for the related prolonged system
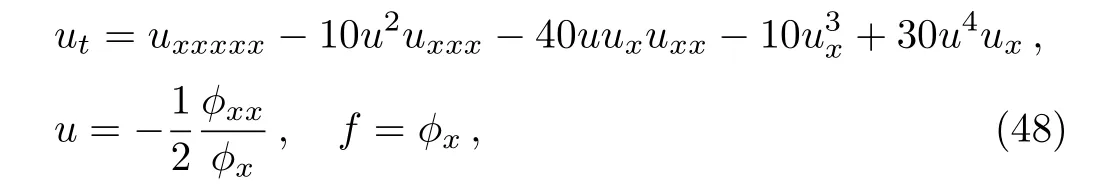
with the Lie point symmetry vector
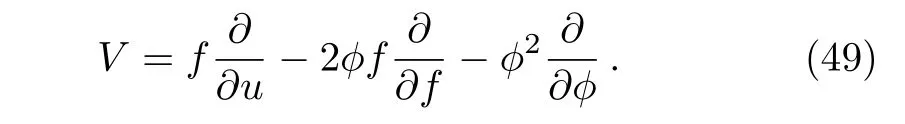
The initial value problem(45)is correspondingly transformed
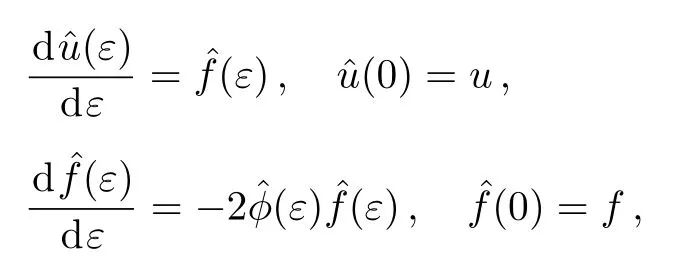
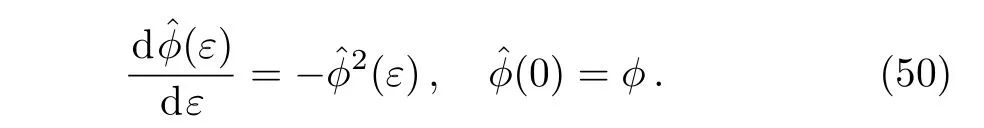
The solution of the above initial value problem(50)leads to the following BT theorem for the prolonged system(48).
Theorem 4If{u,f,?}is a solution of the prolonged system(48),so is{?u,?f,??}with
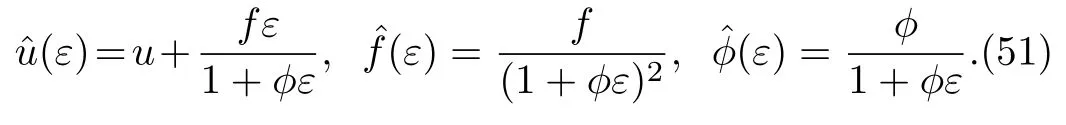
It is worth noticing that the nonlocal residual symmetry(36)is just the infinitesimal form of the symmetry group transformation(51).Furthermore,if we set
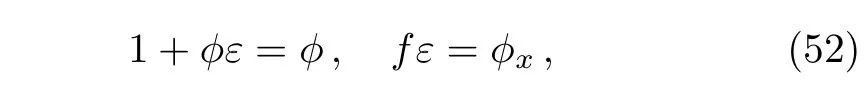
then the first equation of Eq.(51)is nothing but the truncated Painlev′e expansion(37)with Eq.(38).
5 Summary and Discussion
In summary,the fmKdV equation is proved to be CRE integrable and abundant interaction solution between the soliton and the cnoidal periodic waves including arbitrary constants are obtained.Meanwhile,for the fmKdV equation,the nonlocal symmetry related to the CTE is derived.Under the transformation?=1/(1? tanh(w)),this kind of nonlocal symmetry is changed as the residual symmetry which can be obtained obtained with the truncated Painlev′e method.We find that the residual symmetry is just the spectral function symmetry and derive the Lax pair of the fmKdV equation.To solve the initial value problem related by the residual symmetry,the residual symmetry is readily localized to Lie point symmetry by introducing multiple new dependent variables,the corresponding finite transformation group is found by solving the initial value problem of the Lie’s first principle.
In addition,the CRE method is a powerful method for dealing with exact interaction solutions to NLEEs.The relationship between the CRE and the consistent sinecosine expansion is an interesting problem,and we hope to investigate it further in the future.
Acknowledgments
The authors are grateful to Profs.Y.Chen and B.Li for their helpful suggestions and fruitful discussion.
References
[1]C.S.Gardner,J.M.Green,M.D.Kruskal,and R.M.Miura,Phys.Rev.Lett.19(1967)1095.
[2]V.B.Matveev and M.A.Salle,Darboux Transformations and Solitons,Springer,Berlin(1991).
[3]C.Rogers and W.K.Schief,B?cklund and Darboux Transformations Geometry and Modern Applications in Soliton Theory,Cambridge University Press,Cambridge(2002).
[4]R.Hirota,Phys.Rev.Lett.27(1971)1192.
[5]J.Weiss,M.Taboe,and G.Carnevale,J.Math.Phys.24(1983)522.
[6]S.Y.Lou,Phys.Lett.A 151(1990)133.
[7]M.L.Wang,Y.B.Zhou,and Z.B.Li,Phys.Lett.A 216(1996)67.
[8]W.Mal fliet and W.Hereman,Phys.Scr.54(1996)563.
[9]X.Y.Tang,S.Y.Lou,and Y.Zhang,Phys.Rev.E 66(2002)046601.
[10]S.Y.Lou,Residual Symmetries and B?cklund,Transformations,arXiv:1308.1140v1.
[11]X.N.Gao,S.Y.Lou,and X.Y.Tang,J.High Energy Phys.05(2013)029.
[12]S.Y.Lou,Stud.Appl.Math.134(2015)372.
[13]S.Y.Lou,X.P.Cheng,and X.Y.Tang,Chin.Phys.Lett.31(2014)070201.
[14]C.L.Chen and S.Y.Lou,Chin.Phys.Lett.30(2013)110202.
[15]W.G.Cheng and B.Li,Z.Naturforsch.A.71(2016)351.
[16]W.G.Cheng and B.Li,Adv.Math.Phys.2016(2016)4874392.
[17]B.Ren,J.Yu,and X.Z.Liu,Commun.Theor.Phys.65(2016)341.
[18]W.G.Cheng,B.Li,and Y.Chen,Commun.Theor.Phys.63(2015)549.
[19]D.Yang,S.Y.Lou,and W.F.Yu,Commun.Theor.Phys.60(2013)387.
[20]B.Ren,Phys.Scr.90(2015)065206.
[21]Y.H.Wang,Appl.Math.Lett.38(2014)100.
[22]X.R.Hu and Y.Q.Li,Appl.Math.Lett.51(2016)20.
[23]A.Choudhuri,B.Talukdar,and U.Das,Z.Naturforsch.A.64(2009)171.
[24]T.Zhou,Z.N.Zhu,and P.He,Sci.China Math.56(2013)123.
[25]C.Kwak,J.Differential Equations 260(2016)7683.
[26]A.J.Keane,A.Mushtaq,and M.S.Wheatland,Phys.Rev.E 83(2011)066407.
[27]W.G.Cheng,B.Li,and Y.Chen,Commun.Nonlinear Sci.Numer.Simul.29(2015)198.
[28]B.Ren,X.P.Cheng,and J.Lin,Nonlinear Dyn.86(2016)1855.
[29]B.Ren,Commun.Nonlinear Sci.Numer.Simulat.42(2017)456.
 Communications in Theoretical Physics2017年6期
Communications in Theoretical Physics2017年6期
- Communications in Theoretical Physics的其它文章
- A Pair of Resonance Stripe Solitons and Lump Solutions to a Reduced(3+1)-Dimensional Nonlinear Evolution Equation?
- New Patterns of the Two-Dimensional Rogue Waves:(2+1)-Dimensional Maccari System?
- Coherent-State Approach for Majorana Representation?
- Two-Body Local-Momentum Approximation of Spinless Particles Scattered by a(1+1)-D Woods–Saxon Barrier Potential
- Exhibition of Monogamy Relations between Entropic Non-contextuality Inequalities?
- Quantum Coherence Quantifiers Based on R′enyi α-Relative Entropy?
