Synchronization Transition of Time Delayed Complex Dynamical Networks with Discontinuous Coupling?
Yong-Zheng Sun(孫永征), Wang Li(李望),and Dong-Hua Zhao(趙東華)2School of Mathematics,China University of Mining and Technology,Xuzhou 22008,China
2School of Mathematical Sciences,Fudan University,Shanghai 200433,China
1 Introduction
In the past few decades,synchronization of complex networks has been extensively investigated in many fields.[1]Understanding the mechanism behind the network synchronization is a central issue in nonlinear science.Many studies initially focused on the synchronization within a network.[2?5]This kind of synchronization is usually called as “inner synchronization”.It has been shown that the inner synchronization of complex dynamical networks depends both on the node dynamics and the topology of the interaction network.[6]However,in the real world,some networks often connect with other networks,synchronization may take place between two or more networks,which was termed “outer synchronization”[7?9]or “synchronization of duplex networks”.[10]Such as the balance between predator-prey networks in ecological communities.[7]The complete outer synchronization[11?12]and generalized outer synchronization[13?14]have been extensively studied.Many methods have been proposed to realize synchronization,e.g.,adaptive control,[15]pinning control,[16?18]impulsive control[19?21]and fi nite-time control.[22?24]
The theoretical investigation of the outer synchronization has focused mainly on the in fl uence of network topologies and node dynamics.However,recent studies have shown that the interactions between networks also play important roles on synchronization.In real-word systems,it is often found that the interactions between two communities or networks may be switched o ffsometimes.In particular,the interactions may be switched on and o ffperi-odically.For example,due to seasonality,the interactions between predator-prey networks in an ecosystem may be activated and depressed periodically in a year.[25?26]It is thus important to study the synchronization of complex networks with on-o ffcoupling.It has been shown that complex networks can realize synchronization even if the network coupling is switched on and o ffperiodically.[25?27]And it has also been shown that the synchronized domain depends on the time scales of the on-o ffperiod and the node dynamics.[25]
The e ff ect of time delays,which arise from a realistic consideration of fi nite communication times and processing speeds,is a key issue that has received considerable attention.[28?31]Time delay extensively exists in many biological and physical systems such as gene regulatory networks and neural networks.[32]It has been discovered that time delays have great in fl uence on the behavior of complex dynamical systems.In the past few years,the synchronization problem of complex dynamical networks with time delays has been an attractive subject of research.[33?34]Despite these investigations,a systematic study of the in fl uence of time delays and discontinuous coupling on the synchronization transition of complex networks has been lacking.
Inspired by the above analysis,the question which we address in our present study is:Whether the synchronization can be achieved if the coupling between two time delayed complex networks is discontinuous,and if this is the case,under what conditions does it emerge?We propose two time-delayed complex dynamical networks with periodical on-o ffcoupling.First,we consider dynamical networks with constant delay which assume that all nodes in networks react to information received from its neighbours with the same time delay.Later,we investigate the networks with random distributed delays.We focus on the e ff ect of the coupling strength,the on-o ffrate,the network size and the time delay on the synchronization transition.Utilizing the stability theory of differential equations,we analytically show that two networks may realize synchronization if the time delay less than a positive threshold,and the coupling strength and the on-o ffrate are large enough.
The rest of this paper is organized as follows.In Sec.2,networks formulation and some numerical results are given.The stability analysis and sufficient conditions for synchronization are provided in Sec.3.The e ff ect of time delays on the synchronization transmission is discussed in Sec.4.Finally,some conclusions are provided in Sec.5.
2 Synchronization of Networks with Constant Delay
We consider the following coupled drive-response complex dynamical networks:
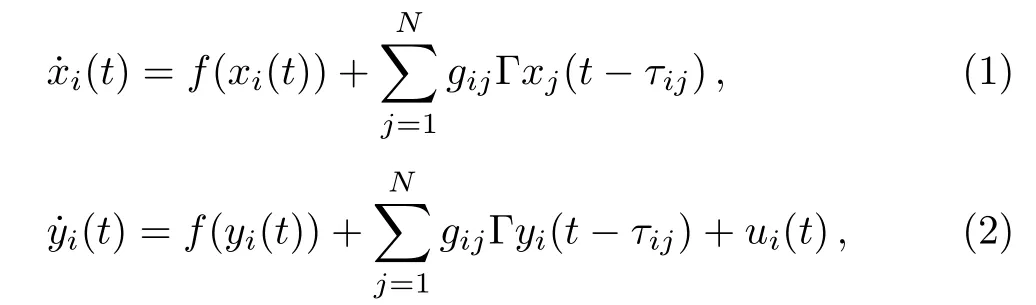
where i=1,2,...,N.Here xi(t)=(xi1,xi2,...,xin)T∈Rnand yi(t)=(yi1(t),yi2(t),...,yin(t))T∈Rnare state vectors of networks(1)and(2),respectively.f:Rn→Rnis the continuously differentiable nonlinear vector function governing the evolution of the i-th node of networks(1)and(2).The adjacency matrix G=(gij)N×Ndescribes the coupling con figurations of both networks:gij>0 if there is a link from node j to node i(i≠j)and zero otherwise,the diagonal elements of matrix G are de fi ned as gii=Γ ∈ Rn×nis the inner connection matrix between two connected nodes,and τijis the delay time in the interaction between the i-th and the j-th nodes.In order to describe the periodic on-o ffcoupling,the controllers ui(t)(i=1,2,...,N)are designed as follows:
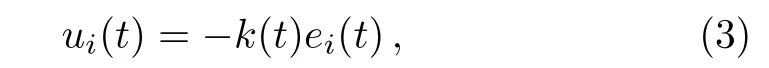
where ei(t)=yi(t)?xi(t)(i=1,2,...,N)are the synchronization errors between the drive network(1)and the response network(2);k(t)is the coupling strength which is taken as the periodic on-o ffcoupling.Speci fically speaking,the network is switched on with k(t)=k when mT≤t≤(m+θ)T,and the network is switched o ffwith k(t)=0 when(m+θ)T≤t≤(m+1)T(m=0,1,2,...),and the two processes are repeated again and again.Here,T>0 is called as the on-o ffperiod;0<θ≤1 is called as the on-o ffrate,while θ=1,corresponds to the continuous coupling case.
In previous works in the field of synchronization of complex networks with on-o ffcoupling,[25?27]the interactions between nodes are assumed to occur instantaneously.However,the e ff ect of time-delayed interactions,which arise from a realistic consideration of fi nite reaction speed,should be considered.In our model,we suppose that nodes in both networks react to information received from its neighbours with some time delays.This is the main di ff erence between previous works and ours.We firstly assume the time delay τijto be the same for all nodes,i.e.,τij≡ τ,so that at time t nodes react to information perceived at time t? τ.Later,we also consider a generalized network model in which we assume that the time delay τijare randomly distributed.
First,we performed a systematic numerical study of the delayed networks(1)and(2)to characterize their synchronization behavior in dependence on the values of parameters k and θ.The simulations were done by choosing the initial conditions xi(0)and yi(0)randomly in the interval[?1,1],for t ∈ (?τ,0].We consider two different topologies including the Erd¨os–R′enyi random(ER random)and the small-world networks with mean degree 〈d〉=6.The small-world network was generated by using the method in Ref.[35]with characteristic parameter p=0.3.We assume that the inner connection matrix Γ=Inand set gij=1 if there is a link between nodes i and j.We took the R¨ossler system as the node dynamics for both networks,which is described by:=[?y?z,x+ay,b+(x?c)z]with a=b=0.2 and c=5.7.We present results for τ=0.01 and T=0.1,but we have found similar results for other values of τ and T.We performed the simulations over the time interval[0,Ts]with Ts=10,and time step ?t=10?3.Note that we choose the values of τ to be integer multiples of ?t.Networks(1)and(2)are said to achieve complete outer synchronization if,for any initial states xi(0),yi(0),
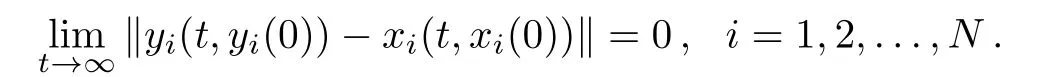
To characterize the transition to synchronization we use the indicator
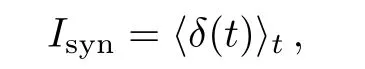
where
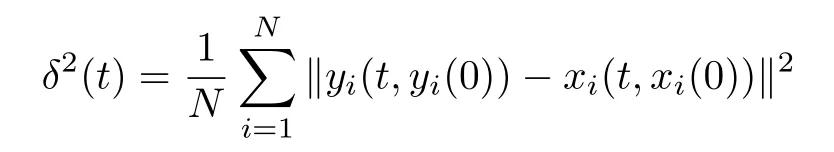
anddenotes an average over the time interval[Ts?1,Ts].
In Fig.1(a),we plot the indicator Isynas a function of the coupling strength k for fixed on-o ffrate θ=0.5.Figure 1(b)displays Isynvs.θ for fixed coupling strength k=5.As Figs.1(a)and 1(b)show for two canonical network models(ER random and small-world networks),the coupled networks(1)and(2)can transit to synchronization as the coupling strength k or the on-o ffrate θ increases.This is further supported by Figs.2(a)and 2(b),where we plotted simulation results for networks(1)and(2)with different values of(k,θ).We divided the domain[0.1,5]× [0.1,1]for(k,θ)into 50 × 50 equidistant(k,θ)-pairs.For each pair of the parameter values we performed simulations over the time interval[0,Ts],and calculated the indicator Isyn.It can be observed that two networks can transit to synchronization as the values of θ and k increase.Taking these results together,we find that two discontinuously coupled networks(1)and(2)can realize synchronization if the coupling strength and the on-o ff rate are large enough.
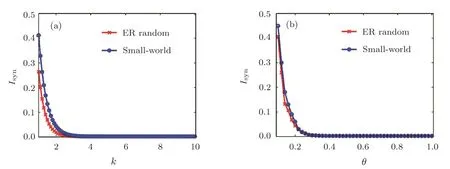
Fig.1 Impact of the coupling strength k and the on-o ffrate θ on the synchronization transition.(a)The synchronization indicator Isynas a function of k for ER random and small-world networks with N=200 and=6;(b)Isynvs. θ.The characteristic parameter for the small-world network is p=0.3.The time delay τ=0.01,and the on-o ffperiod T=0.1.The node dynamics for networks(1)and(2)are the R¨ossler oscillators.
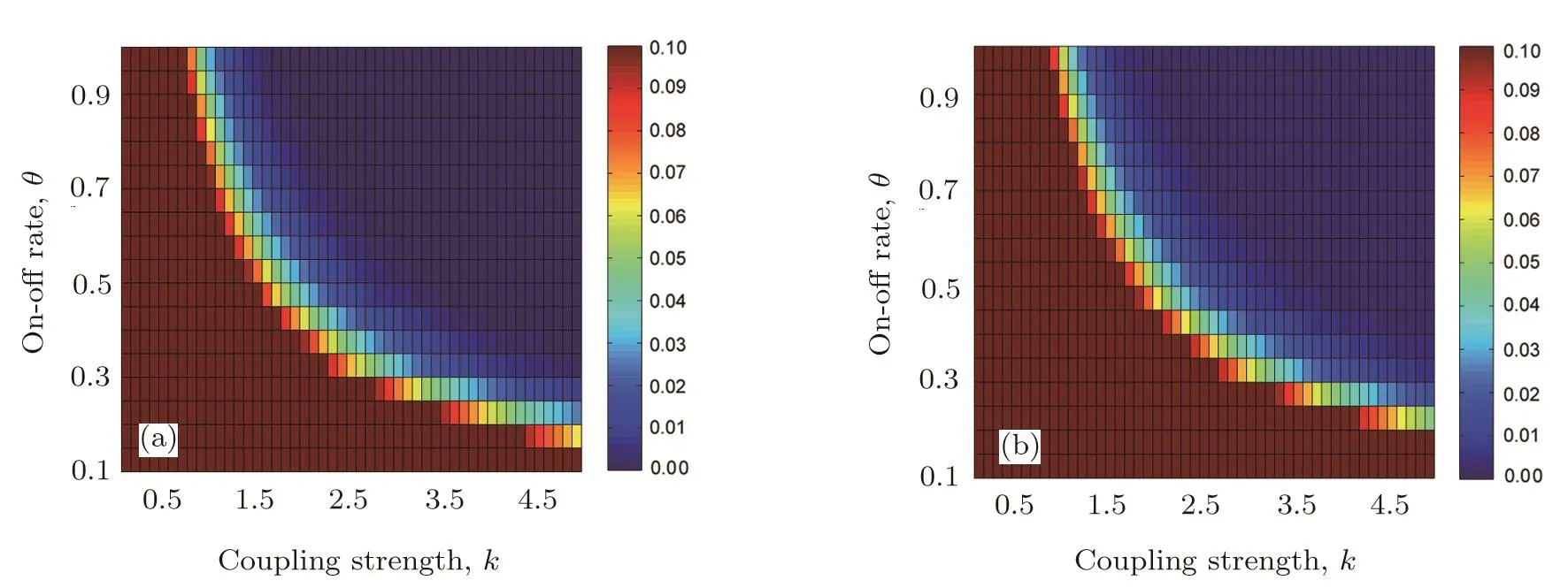
Fig.2 (a)The synchronization indicator Isynfor ER random networks(1)and(2)with N=200 and mean degree =6.The parameters are τ=0.01,T=0.1,and(k,θ) ∈ [0.1,5]× [0.1,1].The dark blue regions indicate numerical synchronization.(b)Same as in(a)but for small-world networks with characteristic parameter p=0.3.
3 Stability Analysis
To understand the factors that determine the synchronization,we propose an analytical synchronization condition using the stability theory of the time-delayed differential equations.For later use,we need the following lemmas.
Lemma 1[36]Let v(t)>0 for t∈R,τ≥ 0.If α> β>0 and
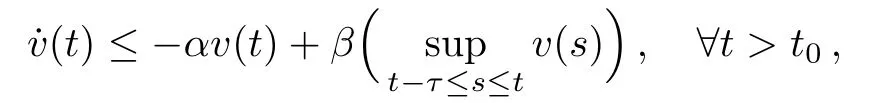
then there exist two positive constants C and α such that
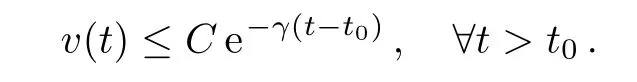
Using Eqs.(1)and(2),we can get the following error systems:
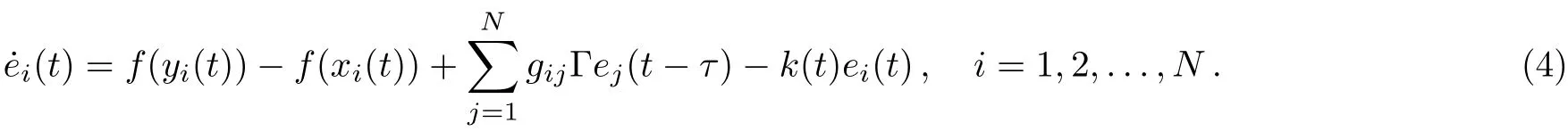
Now let us focus on the stability of the synchronized state.Linearizing the above error systems around xi,one has
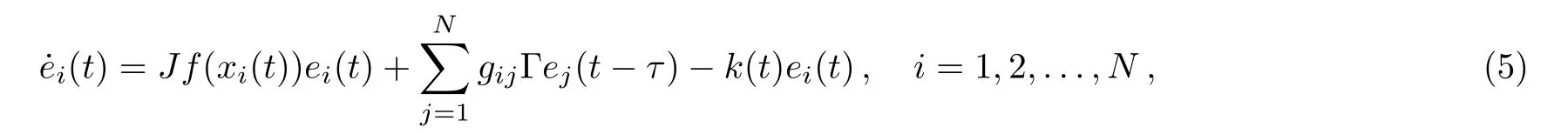
where J denotes the Jacobian operator.
From the Definition of the on-o ffcoupling function k(t),systems(5)can be regarded as switched time delayed systems composed of the following two individual systems:
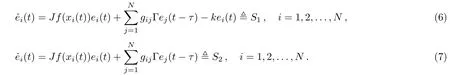
In light of the result in Ref.[37],the error systems(5)are asymptotically stable if the convex combination of the time-delay systems(6)and(7)is asymptotically stable.Thus the stability of the error systems(5)is equivalent to the following time delayed systems:
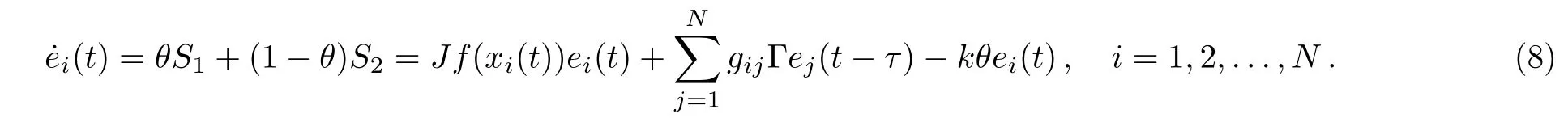
Letting e(t)=and F(t)=((Jf(x1(t))e1(t))T,...,(Jf(x2(t))e2(t))T)T,we can rewrite Eqs.(8)as the following vector form:

where G=Using the fact that e(t)?e(t?τ)=we have
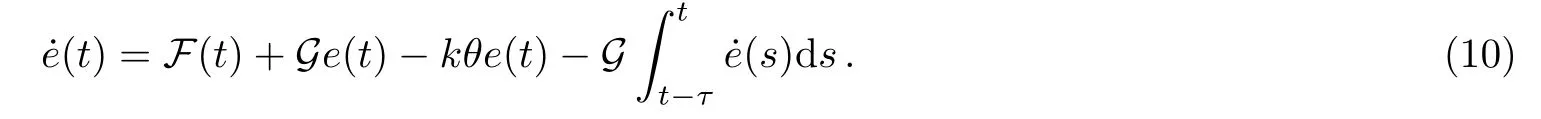
Now,de fi ning the Lyapunov function V=eT(t)e(t),then the derivative of V along the trajectory of Eq.(10)is
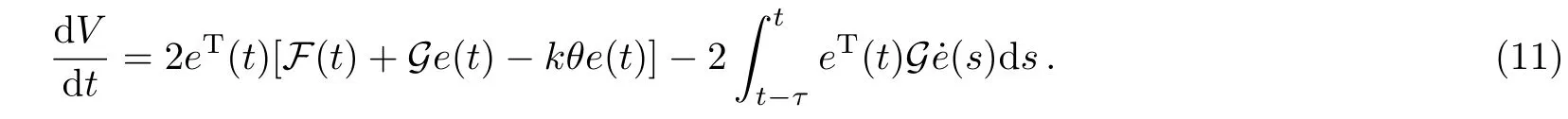
First of all,if the vector function f satis fi es the Lipschitz condition with a positive constant l,we get
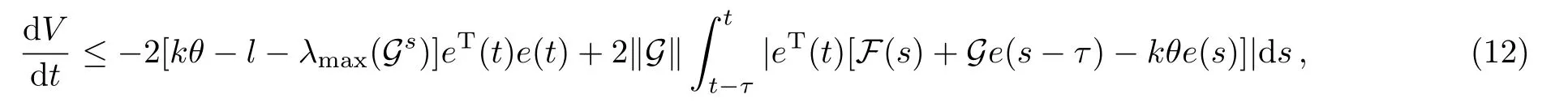
where Gs=(G+GT)/2,λmax(Gs)denotes the maximum eigenvalue of the matrix Gs,and ∥G∥ is the spectral norm of the matrix G.For the last term of right-hand side in Eq.(12),we get
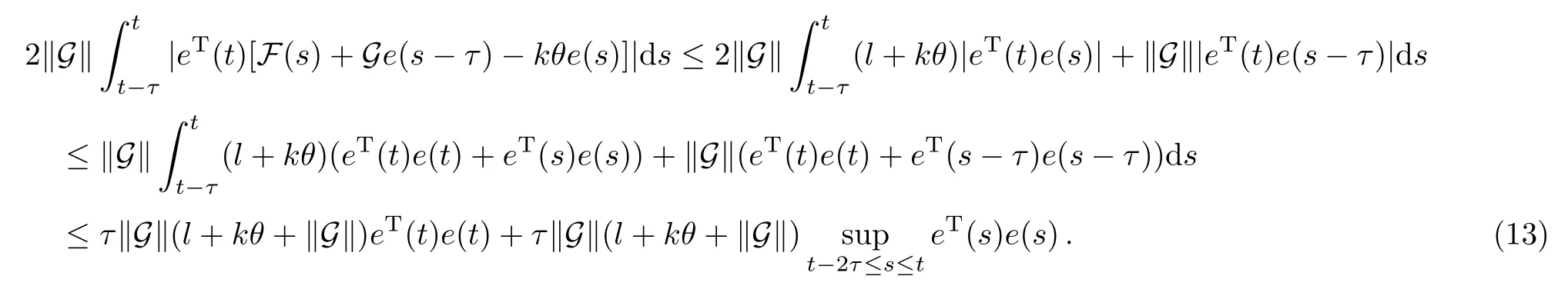
Substituting Eq.(13)into Eq.(12) finally leads to
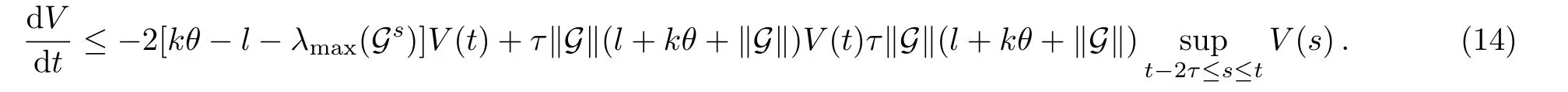
Furthermore,if
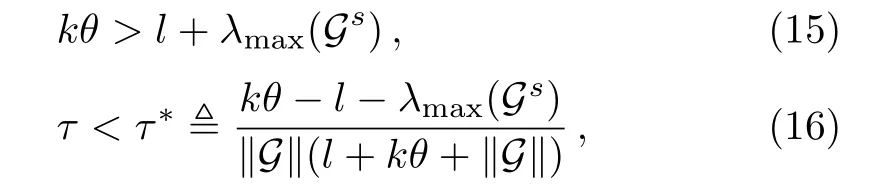
we can obtain from the Lemma 1 that there are positive constants C and γ such that
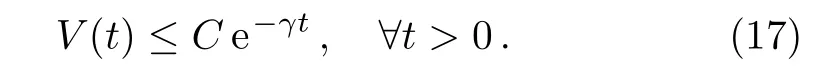
Consequently,
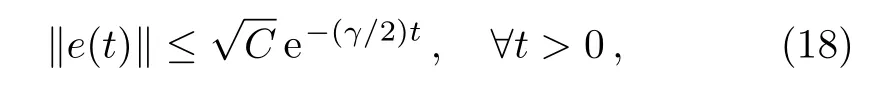
which means that the linear error systems(5)are asymptotically stable about their zero solutions.Therefore,networks(1)and(2)can realize locally complete outer synchronization if the conditions(15)and(16)hold.Thus,if the time delay is less than a positive threshold τ?,the stability of the synchronous state is determined by the coupling strength k and the on-o ffrate θ.This is in accord with the numerical results in Figs.1 and 2.
Furthermore,the allowable bound of the coupling delays is given in terms of explicit expressions,as shown in the inequality(16).In particular,if the adjacency matrix G is symmetric and irreducible,then the eigenvalues of the matrix G are 0= λ1> λ2≥ ···≥ λN.[38]Moreover,if we choose Γ =I,then λmax(Gs)=0 and ∥G∥ =|λN|.Consequently,the synchronization conditions(15)and(16)can be simpli fi ed as
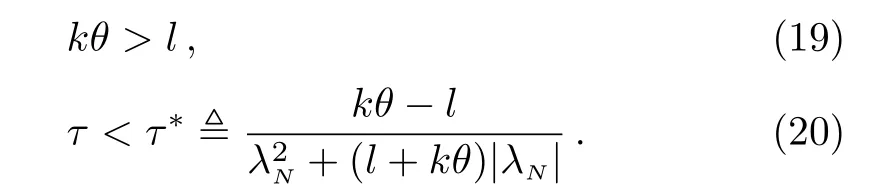
It is known that for inner synchronization of complex dynamical networks without coupling delays,the synchronization ability depends on the second largest eigenvalue λ2or the ratio λ2/λNof the corresponding coupling matrix.[39]However,we can observe from the condition(20)that,for outer synchronization of time-delayed networks with on-o ffcoupling,the synchronization ability depends on the minimum eigenvalue of the coupling matrix.The eigenvalue λNof some network topologies decreases dramatically asNincreases.Thus,the upper bound τ?decreases asNincreases.For example,for the global and star coupling con figurations λN= ?Nand τ?=(kθ?l)/[N2+(kθ+l)N].Therefore,for these kind of networks,the condition(20)implies that the larger of the network size is,the smaller τ?is,and the network is more difficult to be synchronized.
4 E ff ect of Time Delays
Let us now investigate the in fl uence of coupling delays on the synchronization transition.We illustrate our finding using the ER random and small-world networks.We performed simulations of networks(1)and(2)with k=10,θ=0.5,T=0.1,N∈ [10,500]and τ∈ [0,0.5].For the ER random network,we can observe from Fig.3(a)that the minimum eigenvalue of the adjacency matrix decreases as the network size increases.Figure 3(b)displays the value of τ?(N)calculated by the condition(20).It clearly shows that,for random topology,the theoretically upper bound of the time delay for synchronization is signi ficantly decreased as the network sizeNincreases,and τ?≈ 0 whenN&300.Thus high levels of time delay may suppress the synchronization.This observation is fully supported by Fig.4(a),where we divide the domain[10,500]×[0,0.5]for(N,τ)into 50×100 equidistant(N,τ)-pairs and encode the synchronization indicator Isyn.The dark blue regions indicate the numerical synchronization.This is further supported by Figs.5(a)and 5(b)where we plotted evolutions of synchronization error δ(t)between networks(1)and(2)forN=100,k=10,θ=0.5,T=0.1 and τ=0.03(Fig.5(a)),and τ=0.04(Fig.5(b)).We observe that two networks can achieve outer synchronization for τ=0.03,but they do not show tendency to synchronization for τ=0.04.different from the ER random network,Figs.3(a)and 3(b)show that,for the small-world network,λNis not a decreasing function of the network size.Thus,the upper bound of the time delay for synchronization for the small-world network is only weekly in fl uenced by the network size(Fig.4(b)).
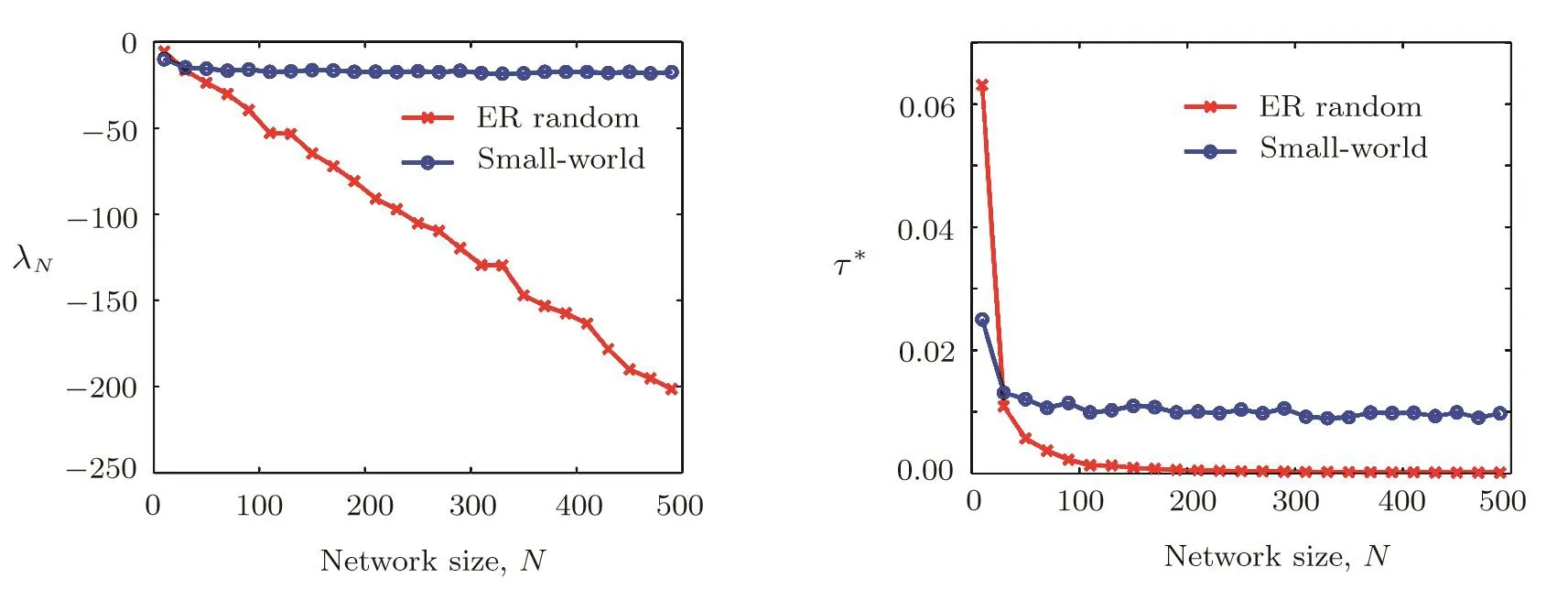
Fig.3 The e ff ect of network size N on the minimum eigenvalue λNand τ? calculated using Eq.(20)for ER random and small-world networks.(a)λNvs.N;(b)τ?vs.N.Both ER random and small-world network have mean degree〈d〉=6 and the characteristic parameter for the small-world network is p=0.3.The other parameter values are k=10,θ=0.5.
In the above numerical and analytical studies,we assume that all the interactions occur with the same delay.However,actual delays in real systems are not necessarily the same for all the nodes in the networks.Delays might also be randomly distributed.Let us now consider the e ff ect of random delay times on the transition of synchronization.Speci fically,we consider random delays with the following normal distribution: τij= τ+ξ,where ξ is normally distributed with zero mean and standard deviation one.The delays are normally distributed around with mean τ and variance 1.Figures 6(a)and 6(b)display the synchronization indicator Isynas the function of the mean coupling delay τ and the network sizeN.Similar to the case of constant delays,it can be observed from Fig.6(a)that,for the ER random networks,the upper bound of the mean time delay for synchronization decreases with the network size increasing.Compared with the numerical results in Fig.4(a),the upper bound of the mean coupling delay for synchronization of the ER random network is smaller than that of networks with constant coupling de-_lay.It can be observed from Figs.4(b)and 6(b)that,for small-world networks with normally distributed coupling delays,the upper bound of the mean time delay for synchronization is larger than that of networks with constant delay.When the size of the network becomes larger,the above numerical results show that networks with smallworld topologies can tolerate larger delays than ER random networks.
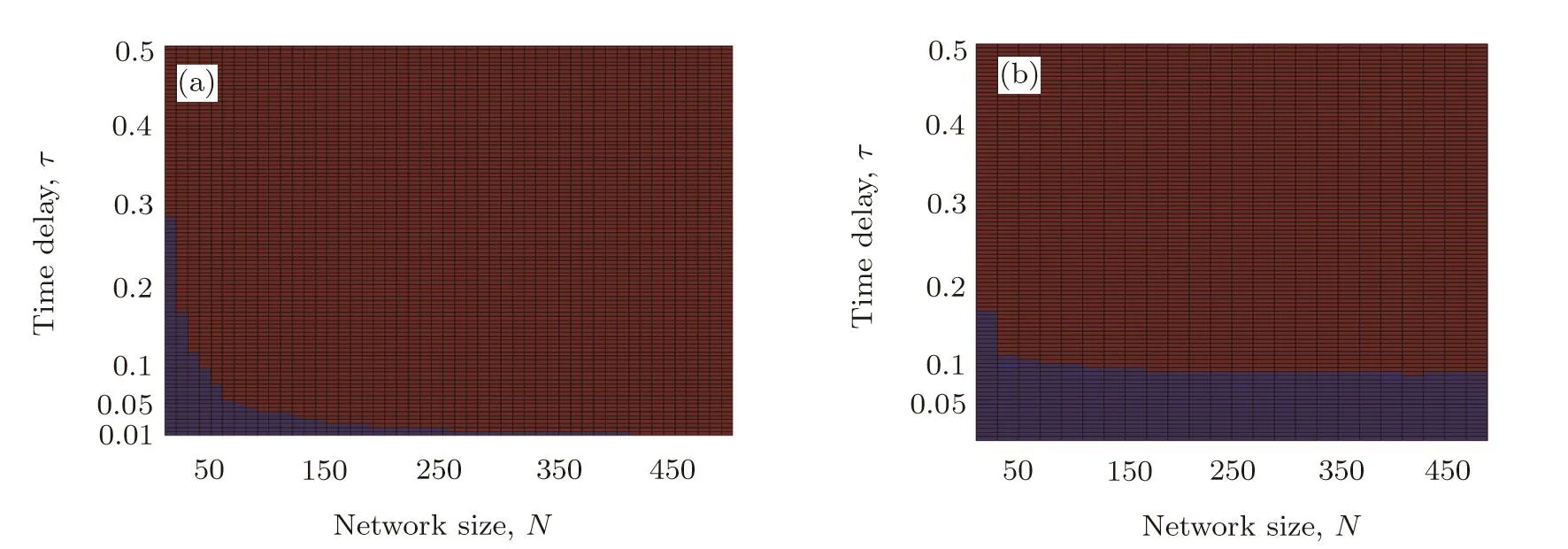
Fig.4 Effect of the time delay and network size on the synchronization transition for ER random(a)and small-world(b)networks with mean degree〈d〉=6.The parameters for networks(1)and(2)are k=10,θ =0.5,T=0.1 and(N,τ)∈ [10,500]×[0,0.5].The characteristic parameter for the small-world network is p=0.3.The dark blue regions indicate numerical synchronization.
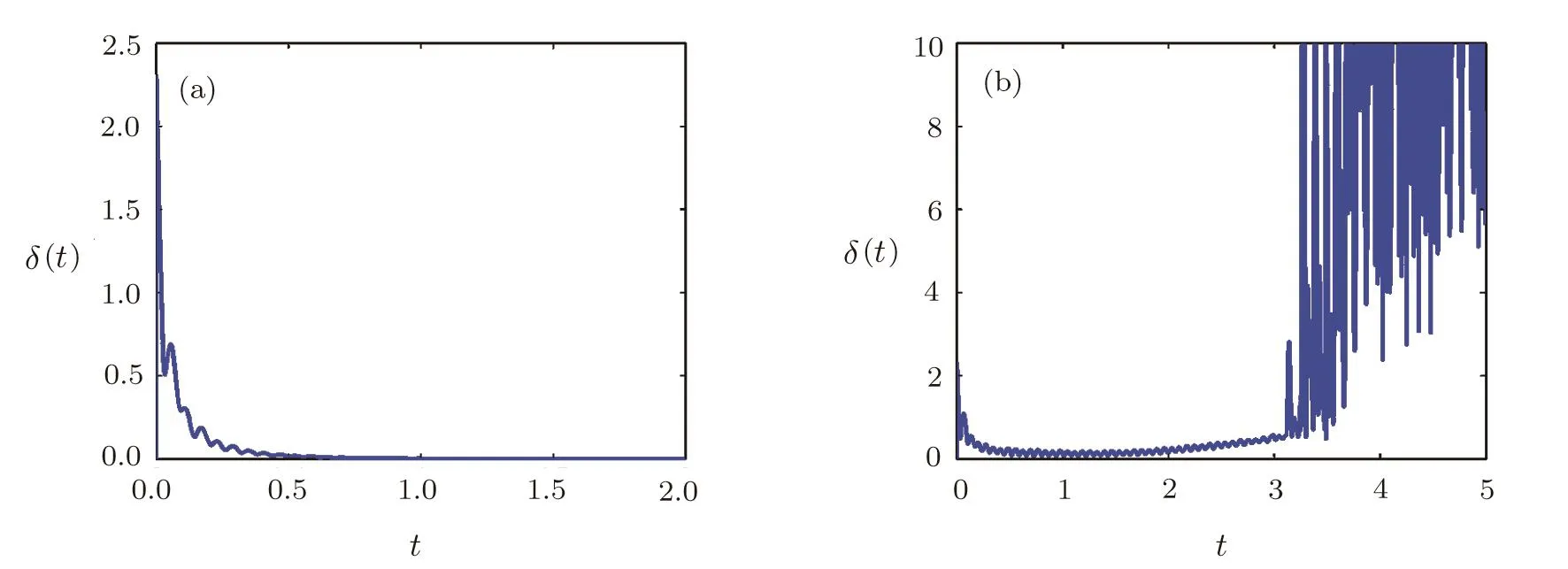
Fig.5 Synchronization error δ(t)between ER random networks(1)and(2)with N=100,k=10, θ =0.5,T=0.1,p=0.1.(a)The time delay τ=0.03;(b)The time delay τ=0.04.
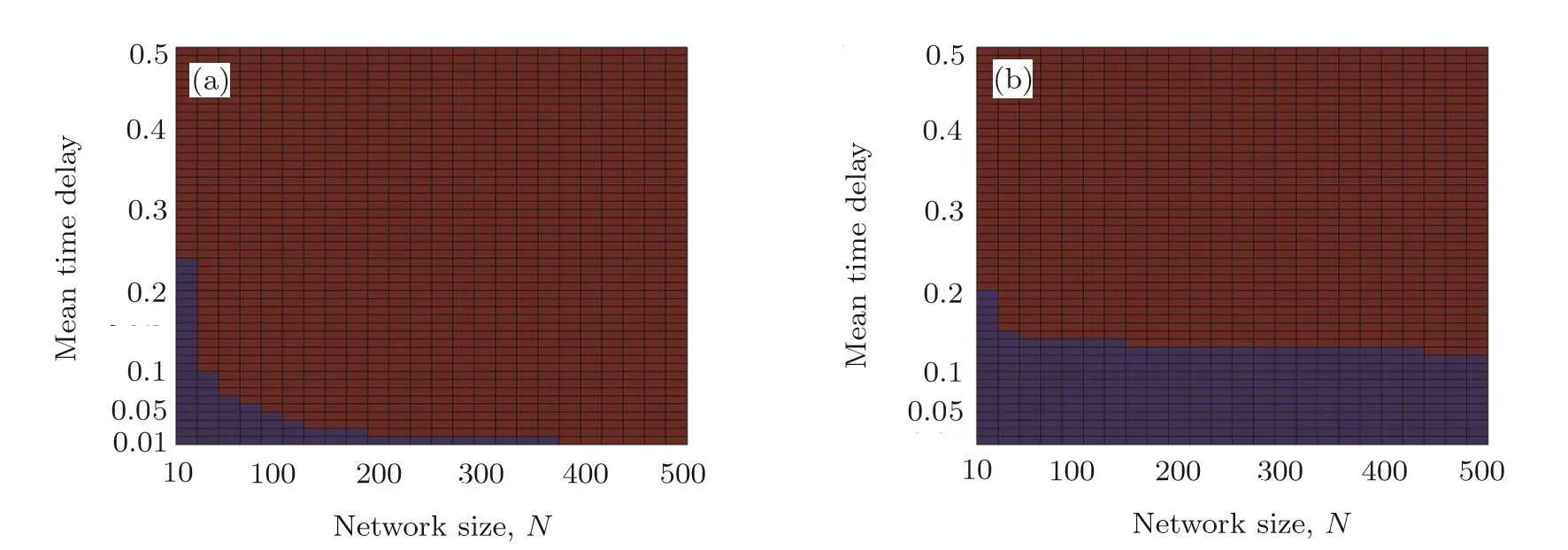
Fig.6 Synchronization indicator Isynfor(a)ER random and(b)small-world networks with normally distributed coupling delay.The parameter values used are k=10,θ=0.5,T=0.1,p=0.1.Both ER random and smallworld networks have mean degree 〈d〉=6.The characteristic parameter of small-world networks is p=0.3.The dark blue regions indicate numerical synchronization.
5 Conclusions
In this paper,we have investigated the synchronization transition between two time delayed complex dynamical networks with periodic on-o ffcoupling.First,we considered the networks with constant coupling delay.We found that for sufficient large coupling strength and the on-o ff rate two networks can realize synchronization if the coupling delay is small enough.Based on the stability theory of differential equations,sufficient conditions for the outer synchronization are established.The estimation for the upper bound of time delays for synchronization is obtained.Numerical results are fully supported by the theoretical analysis.In particular,we reported that,for the undirected and strongly connected networks,the upper bound of time delays for synchronization is a decreasing function of the absolute value of the minimum eigenvalue of the adjacency matrix.The e ff ect of random delays on the transition of synchronization is also investigated.We found that when the network size is large,small-world networks can tolerate larger time delay than ER random networks.
Acknowledgments
We thank the anonymous referees for their helpful comments and suggestions.
References
[1]A.Arenas,A.D?az-Guilera,J.Kurths,Y.Moreno,and C.Zhou,Phys.Rep.469(2008)93.
[2]J.L¨u,X.Yu,and G.Chen,Physica A 334(2004)281.
[3]Q.Zhang,J.Chen,and L.Wan,Phys.Lett.A 377(2013)2754.
[4]T.Pyragien.e and K.Pyragas,Phys.Lett.A 379(2015)3084.
[5]X.Liu and T.Chen,IEEE T.Automat.Contr.60(2015)3316.
[6]T.Nishkawa,A.E.Motter,Y.C.Lai,and F.C.Hoppensteadt,Phys.Rev.Lett.91(2003)014010.
[7]C.Li,C.Xu,W.Sun,and J.Kurths,Chaos 19(2009)013106.
[8]X.Wu,W.Zheng,and J.Zhou,Chaos 19(2009)013109.
[9]W.Sun,Y.Wu,J.Zhang,and S.Qin,J.Frank.Inst.352(2015)3166.
[10]Y.Li,X.Wu,J.Lu,and J.L¨u,IEEE T.Circuist-II 63(2016)206.
[11]G.Wang,J.Cao,and J.Lu,Phys.A 389(2010)1480.
[12]Y.Sun,W.Li,and J.Ruan,Commun.Nonliear Sci.18(2013)989.
[13]W.Sun and S.Li,Nonlinear Dyn.77(2014)481.
[14]Y.Wu,C.Li,Y.Wu,and J.Kurths,Commun.Nonlinear Sci.17(2012)349.
[15]H.G.Zhang,M.Zhao,Z.L.Wang,and Z.N.Wu,Nonlinear Dyn.77(2014)643.
[16]X.Li,X.Wang,and G.Chen,IEEE T.Circuist-I 51(2004)2074.
[17]W.Yu,G.Chen,J.L¨u,and J.Kurths,SIAM.J.Control Optim.51(2013)1395.
[18]D.Ning,X.Wu,J.Lu,and J.L¨u,Chaos 25(2015)113104.
[19]W.Sun,G.Chen,J.L¨u,and S.Chen,Nonlinear Dyn.69(2012)1751.
[20]J.Lu,D.W.C.Ho,J.Cao,and J.Kurths,Nonlinear Anal.Real.RWA 14(2013)581.
[21]Z.Wu,Commun.Theor.Phys.61(2014)590.
[22]Y.Sun,W.Li,and D.Zhao,Chaos 22(2012)023152.
[23]Y.Sun and W.Lin,Chaos 25(2015)083118.
[24]Y.Sun,W.Li,and J.Ruan,Commun.Theor.Phys.58(2012)697.
[25]L.Chen,C.Qiu,and H.Huang,Phys.Rev.E 79(2009)045101(R).
[26]L.Chen,C.Qiu,H.Huang,G.Qi,and H.Wang,Eur.Phys.J.B 76(2010)625.
[27]Y.Sun,W.Li,and D.Zhao,Chaos 22(2012)043125.
[28]S.Xu and J.Lam,Int.J.Syst.Sci.39(2008)1095.
[29]Q.Wang,G.Chen,and M.Perc,PloS One 6(2011)e15851.
[30]J.Ma,H.Qin,X.Song,and R.Chu,Int.J.Modern Phys.B 29(2015)1450239.
[31]W.Sun,S.Wang,G.Wang,and Y.Wu,Nonlinear Dyn.79(2015)2659.
[32]J.Lu,J.Zhong,D.W.C.Ho,Y.Tang,and J.Cao,SIAM J.Control Optim.54(2016)475.
[33]R.Rakkiyappana,N.Sakthivela,and S.Lakshmananb,Chin.Phys.B 23(2014)020205.
[34]T.Hu,Y.Wu,and S.Li,Commun.Theor.Phys.65(2016)33.
[35]D.J.Watts and S.H.Strogatz,Nature(London)393(1998)440.
[36]A.Hmamed,Int.J.Syst.Sci.22(1991)1127.
[37]J.Chiou,C.Wang,and C.Cheng,J.Frank.Inst.348(2011)261.
[38]C.W.Wu and L.O.Chua,IEEE T.Circuist-I 42(1995)430.
[39]X.F.Wang and G.Chen,IEEE T.Circuist-I 49(2002)54.
 Communications in Theoretical Physics2017年1期
Communications in Theoretical Physics2017年1期
- Communications in Theoretical Physics的其它文章
- Exact Calculation of Antiferromagnetic Ising Model on an Inhomogeneous Surface Recursive Lattice to Investigate Thermodynamics and Glass Transition on Surface/Thin Film?
- Laser Polarization E ff ect on Molecular Harmonic and Elliptically Polarized Attosecond Pulse Generation?
- Higher-Order Corrections to Earth’s Ionosphere Shocks?
- Ground State Properties of Z=126 Isotopes within the Relativistic Mean Field Model?
- Electron-Positron Pair Production in Strong Fields Characterized by Conversion Energy?
- Relativistic Bound and Scattering Amplitude of Spinless Particles in Modi fi ed Schioberg Plus Manning–Rosen Potentials
