O.V.Fesko,I.V.Rasina,Ni Mingkang(1.Departmentof Mathematics,East China Normal University,Shanghai0041,China; .Ailamazyan Program Systems Institute,Russian Academy of Sciences,Pereslavl-Zalessky 1501,Russia)

Improvement algorithms for discrete-time control systems based on the extension and localization principles

O.V.Fesko1,2,I.V.Rasina2,Ni Mingkang1?
(1.Departmentof Mathematics,East China Normal University,Shanghai200241,China; 2.Ailamazyan Program Systems Institute,Russian Academy of Sciences,Pereslavl-Zalessky 152021,Russia)

In this paper,we present iterative improvement algorithms for free-end and constrained discrete-time systems.These algorithms are based on the extension and localization principles.In the case of constrained end problem,a method based on approximation of reachable set is proposed. Algorithm proceduresare illustrated with examples.

optimalcontrol;discrete system;extension principle;localization principle;reachable set; iterative optimization

1 Introduction

Discrete dynamicalmodels form an importantclass ofmathematicalmodels thatcan describe a wide range of real world systems and corresponding to them optimalcontrol problems.There exists a large amountof literatureon methods of optimalcontroland improvements.In general,these existing methods are based on such fundamental resultsasthe maximum principleofPontryagin[1],the dynamic programming method ofBellman[2],and the sufficient conditions ofoptimality of Krotov[3].Itshould be noted thatthe majority of optimalcontrolmethods,both exactand approximate,are designed for continuous time systems.For generaldiscrete systems,especially nonlinear,a set of such methodsis more limited due to the factthatin the generalcase there isno analogue ofthe Pontryagin maximum principle for the discrete-time systems[4?6].

Discrete modelscan be used to solve optimalcontrolproblems(including continuousoneswith priordiscretization of variables)through directapplication of non-linear programming methods[7?10].In terms of optimalcontrol theory the results based on the Bellman principle of optimality and generalsufficientconditions of optimality of Krotov are much more developed.They include,in particular,localoptimality conditionsand iterative improvement methods for discrete and hybrid systems[11?14].

This paperproposes iterative methods of localoptimization for free-end and constrained discrete systems using the extension and localization principles[15?17]and description of the reachable set[15,18?19].The algorithm proceduresare demonstrated by examples.

2 Problem formulation and preliminary results

Consider a controlsystem described by the following equations:

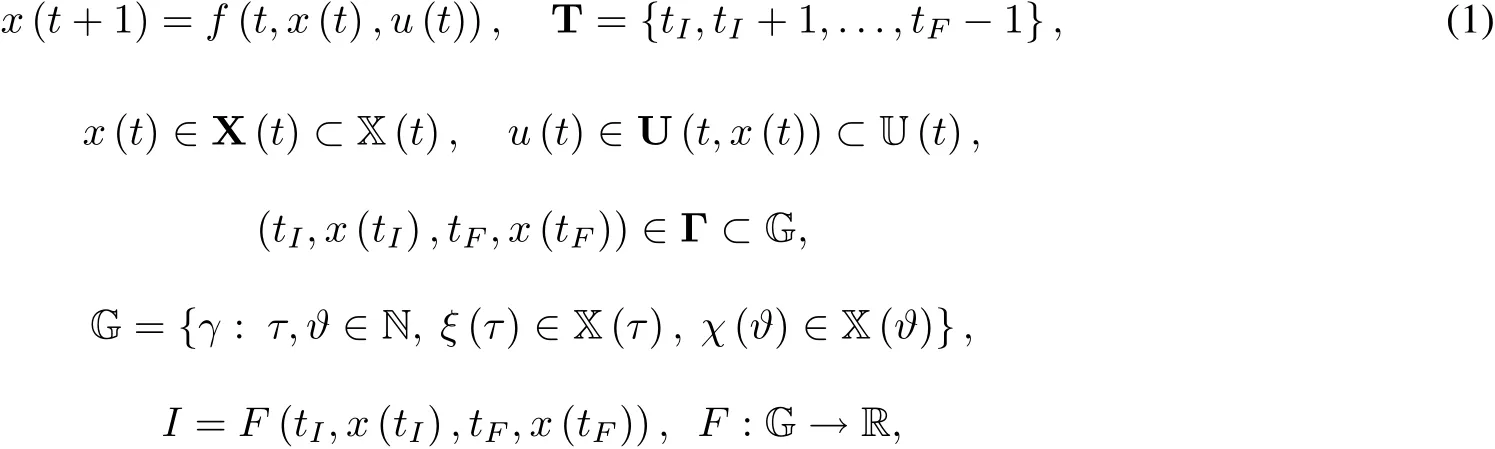
where γ=(τ,ξ(τ),?,χ(?)),X(t),U(t)are the basic sets(spaces)of arbitrary nature,in generaldifferentfor different t.Let T,x(tI)be given,x(tF)∈XF.Assume thatfunctions f(t,x,u)and F(x)have good analytical properties.

We denote by D the set of its possible solutions m=(T,x(t),u(t)).It is required to find a sequence {ms}?D such that I(ms)→I?=.

The essence of the extension principle is the replacement of the problem(D,I)by an analogous problem (E,L),in some sense simpler,which also gives a solution ofthe originalproblem.Extensions(E,L)are defined as follows.The discrete chain(1)is excluded,thereby the set E is uniquely determined.For any t∈N an arbitrary functional

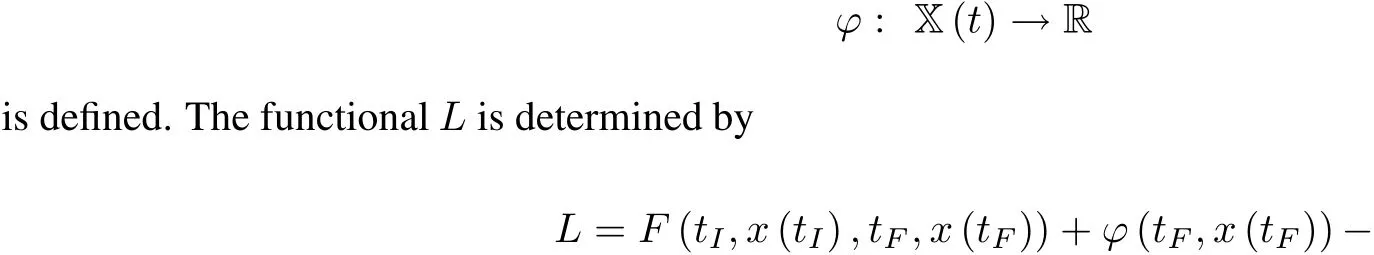
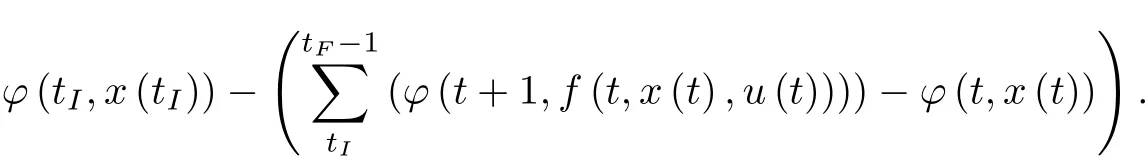
Obviously,L=I for m∈D when constraint(1)is satisfied.Indeed,regrouping the terms gives

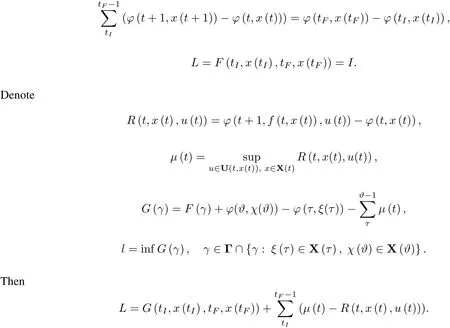
These expressions are used to formulate the following general proposition comprising Krotov sufficient optimality conditionsforthe problem being considered.Denote by Tmaxany segmentof N which covers the projection ofΓon t axis.

Theorem 1(Gurman V.I.[15])Letthere be a sequence{ms}?D and a sequence?q(t),t∈Tmaxsuch that

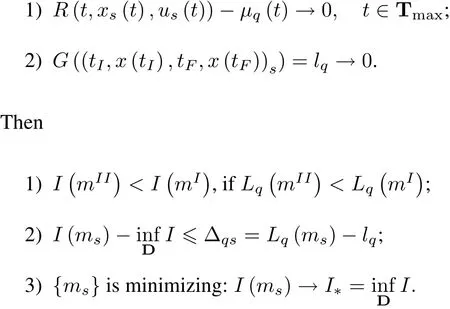
This proposition follows immediately from the extension principle.The theorem reduces optimization problems with discrete recurrent constraints to problems without such constraints,or,in more detail,to mathematical programming problems(minimizing G(γ)and maximizing R(t,x,u)with respect to x and u for various given values of t).

3 Controlimprovementforfree-end discrete problem

3.1 Derivation ofthe improvementalgorithm

Let an element mI=(x(t),u(t))I∈D be given.The problem is to improve mI,that is,to find mII∈D such that I(mII)＜I(mI).Repeating to solve this improvementproblem sequentially,we getan iterative process aimed to minimize the functional I.

The localization principle[15,17]is to reduce the improvementproblem to a globaloptimization fora simplified modelwhich is valid in the vicinity of improving element.According to the localization method,we introduce a family of functionals

The improvementof mIis achieved via minimization of Iαfor the system(1)and(2).

Following the extension principle,we introduce a scalarfunction

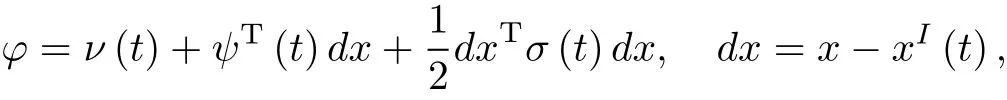
whereν(t),ψ(t)andσ(t)are a scalar,an n-vectorand an(n×n)-matrix functionsrespectively,and the generalized Lagrangian

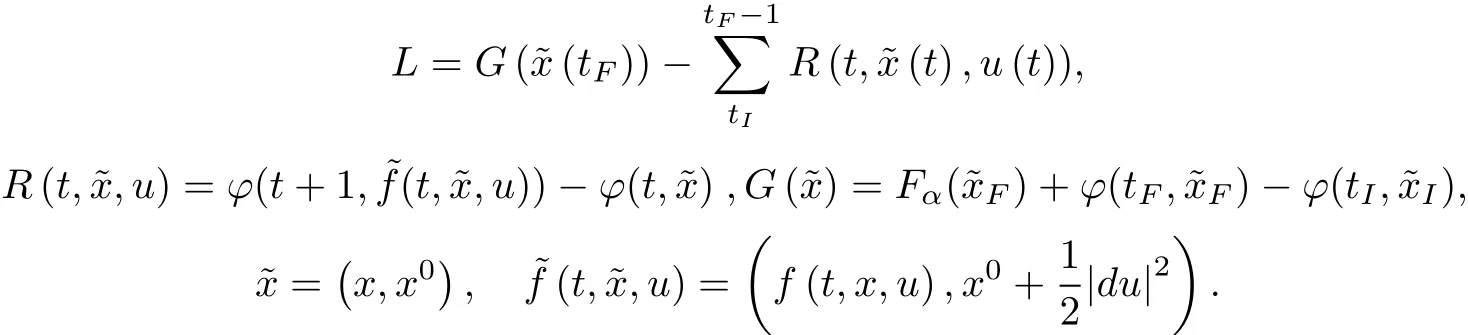
According to the extension principle,the problem ofminimum of Iαforthe system(1)and(2)can be reduced to the minimization problem of L withoutthe discrete chains.

Equations w.r.t.unknown Taylor elements of?can be derived with the help of Taylor approximations of constructions R and G in the neighborhood of(xI(t),uI(t)).The following basic relations for the improvement algorithm are obtained.

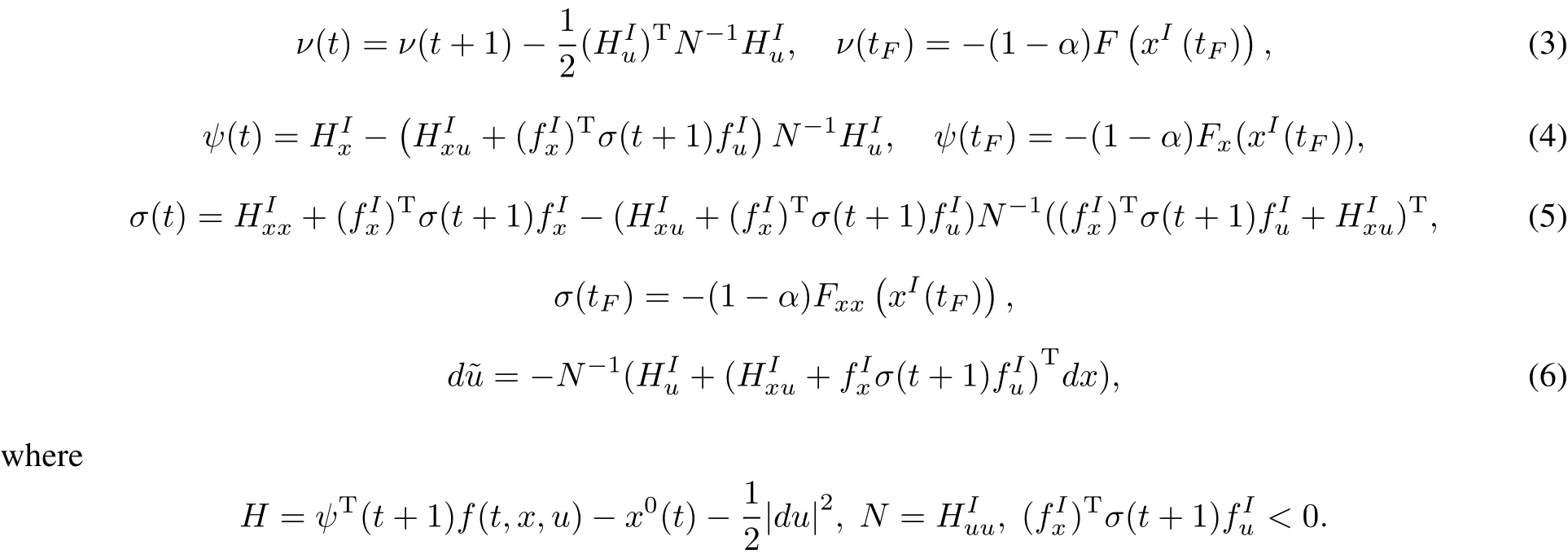
3.2 Iterative improvement algorithm

Thus the following iterative procedure is obtained.

1.Solve Eq.(1)“from the leftto the right”for x(tI)=xI,u=uI(t),t∈T,obtain xI(t).

2.Solve Eqs.(3)–(6)“from the rightto the left”.Check conditionsα=0,=0,N＜0 forevery t atthe same time.Ifthey hold then the improvementprocess finishes.Ifcondition=0 fails then go to 3,otherwise go to 4.

3.Repeat 2 for differentα,choose suchα?that the condition N＜0 holds in the entire set T,andΔα= I(mI)?I(mα)is maximized.Take mα?=mII,uII(t)for uI(t)and go to 1.

4.If the condition N＜0 fails ata certain point t?∈T then choose suchαthatthis condition would hold in the entire set T,exceptpoint tIin which det N=0.Calculateν,ψ,σ.

5.Solve Eq.(1)repeatedly fordifferent∈＞0 with the initialcondition x(tI)=xIand u(t)=uI(t)+du(t), where du(tI)is taken such that N(tI)du=0,|du|＜∈,and following Eq.(6)for t＞tI.Find∈?maximizing Δ∈=I(mI)?I(m∈),then take m∈?for mII,uII(t)for uI(t)and go to 1 to startthe nextiteration.

The overalliterative process is stopped whenα?≈0 and mI≈mIIwith the required accuracy.The final resultis atleasta localminimum and a localapproximate synthesis of optimalcontrol.

Remark 1 If the conditions thatα=0,=0,N＜0 are satisfied,then mI=,delivers a localmaximum to R(t,x,u)w.r.t.(x,u)for all t∈T,a local minimum to G(x)and a local minimum to the functional.If it proves to be not only local,but also global maximum of R(t,x,u)w.r.t.u in the neighborhood of xI(t)then the controlfieldˉu(t,x)=uI(t)+d?u(t,dx)is approximate local optimal control synthesis in an∈-neighborhood of the localminimal.

Remark 2 Assumeσ=0 in Eqs.(3),(4),and(6).Then the above algorithm of the second order becomes the firstorderone:

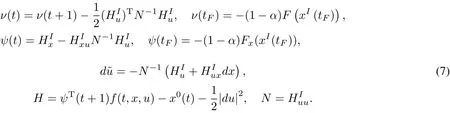
Itis easy to see that the first order algorithm differs fundamentally from the gradientalgorithm.The variation d?u still depends on dx.Thus,as in the case of the second order algorithm,the solution is an approximate optimal linearsynthesis ofcontrol.

Remark 3 Equation forσis the matrix equation of Riccati type which can have a singular point.A point t?is called singular if the matrix Ruuchanges the sign-definiteness in it.In this case the singular point can be placed at point tIat the expense of parameterα,and the variation of control can be obtained from the modified equation[20]:Ruu(tI)du(tI)=0.The latter is a system of homogeneous linear algebraic equations with degenerate matrix Ruu(tI),therefore,a nontrivialsolution always exists.

4 Constrained-end problem

4.1 Reachable sets and its estimates

The reachable setis an importantcharacteristic ofcontrolsystems.The information on reachable set(thatis,its description orestimate)gives a sufficiently complete characterization,which helps to solve various controlproblems, in particularoptimalproblems.

Definition 1 The reachable set XR(t,tI,XI)of controlsystem(1)ata time t generated by a set XIata time tIis the setofelements x(t)thatcan be connected by trajectories ofthe system beginning atthe time tIin XI.

Definition 2 Any set XERthatcontains the reachable setis called its externalestimate.

Then the following equations hold:

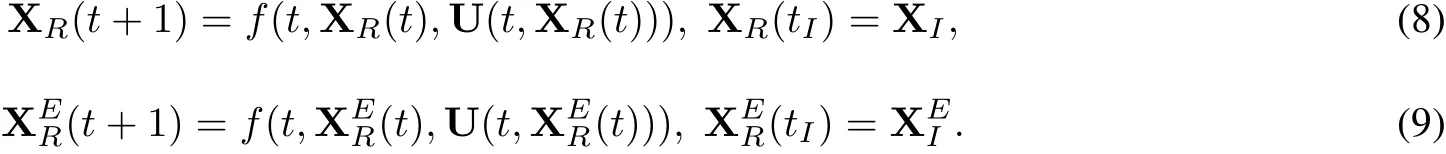
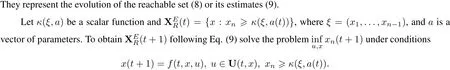
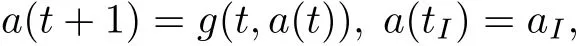
is obtained which represents the evolution of)in terms ofthe given functionκ(ξ,a).

Let x(tF)∈in Eq.(1).Itwas shown in[15]thatan efficientmethod of description of the reachable setallows one to solve strictly optimalcontrolproblems with restrictions atthe rightend.

Carry outa localapproximation ofthe reachable setofthe system(1)and(2).Itis easily seen from Eq.(2)that

be Taylorapproximation ofthe reachable setbound with some nonnegative matrixσ(t).Itcan be presented as

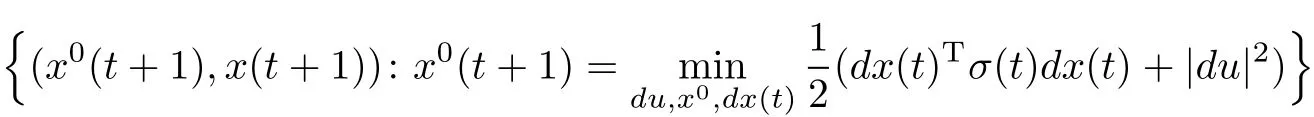
underthe condition

which is linearized system(1)in the vicinity of(xI(t),uI(t)):

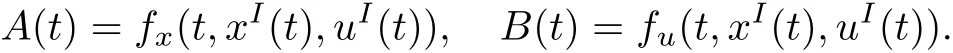
Solve the minimization problem by the Lagrange method:

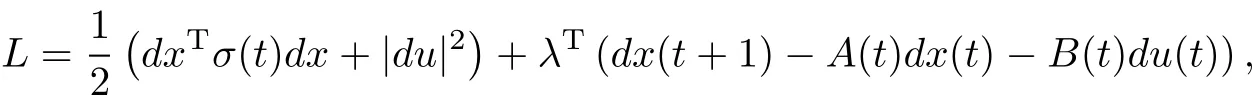
Thus we obtain approximate reachable setthatcan be used to solve the minimization problem of Fα(t,x,x0) with restrictions atthe rightend using the localization method.

4.2 Procedure of controlimprovement

In summary,we getthe following iterative procedure.

1.Solve the linear matrix Eq.(10)for?(tI)=0.

2.Minimize the function

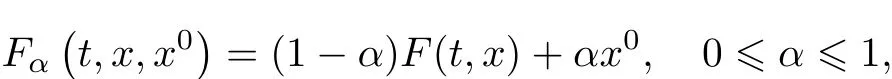
underthe conditions

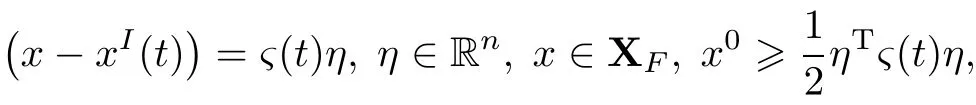
find the minimizing point dxF?(α)=?(tF)η?(α).

3.Calculate chain

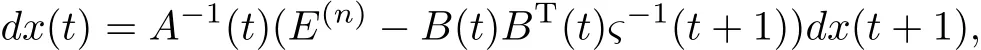
backward starting at dx(tF)=dxF?(α)to obtain dxα(t)and

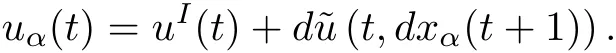
4.Calculate forward chain(1)under uα(t)starting from(tI,xI)to obtain mα=(xα(t),uα(t))andΔ(α)= I(mI)?I(mα).

5.Repeat steps 2-4 for differentαuntil(xα(tF))–condition holds with given accuracy,andΔ(α)is maximized atsomeα?;take mα?for mII.

6.Take mIIfor mIand startthe nextiteration.

The iterative process is over whenα?≈0 and mI≈mIIwith required accuracy.

5 Examples

5.1 Parallelreaction problem

This problem was initially solved in[21]and later e.g.in[22]and[23].Consider a tubular reactor where the following chemicalreactions take place:

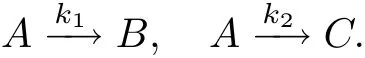
The reaction constants follow Arrhenius kinetics.We considera discrete version of the model:

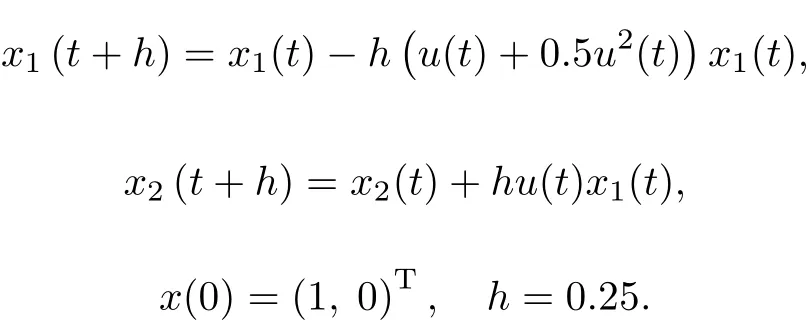
Here,x1(t)=CA/CAfdenotes the dimensionless concentration of A,x2(t)=CB/CBfis the dimensionless concentration of B.The control u(t)=k1L/v is restricted(L is the reactor length,v is the plug flow velocity): 0≤u(t)≤5.The aim of the optimization is to maximize the amount of the product B until the final time: I=x2(1)→max.

The initial approximation for the improvementprocedure is uI=2 and at that I=0.5.In the first step, the above first-order algorithm was applied(Remark 2).The convergence slowed after 3 iterations.Then,in the second step,the second-order algorithm from Subsection was chosen and remained active up to 2-th iteration. The value of the functional was improved to I=0.591841617 that is better than the value I=0.5729 reported in[24]and I=0.572939 obtained in[25].This can be explained,first,by the fact that Eq.(6)contains the matrices ofsecond partialderivatives,and,second,d?u is a linearcontrolsynthesis.The resulting optimalcontrolis u={1.23;1.22;1.35;1.58}.For the comparison only the first-order algorithm was applied with the same initial approximation.Itfound the optimum after15 iterations.

5.2 Optimalhelicopter maneuvering

Considera helicoptermaneuvering problem thatminimizes the transferring time from one point A on the earth surface to another point B with prescribed local altitude along transfer trajectory above the surface.It is assumed thatit’spossible to controlthe velocity instantly within restrictionsthatdepend on engine powerand localdirectional reliefslope angle.

We considerdiscrete motion modelthatwas obtained through discretization of the corresponding differential equation with sufficiently smallstep(1 s):

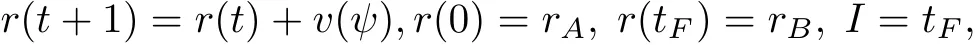
where r=(r1,r2)is the horizontal projection of a spatial geometric point and v=(v1,v2)is the horizontal projection of the flightvelocity,v1=νcosψ,v2=νsinψ,ψis yaw angle(the control),ν(ψ)is the maximum velocity in the direction ofψ.

The calculations were carried outfor the following hypotheticaldata:

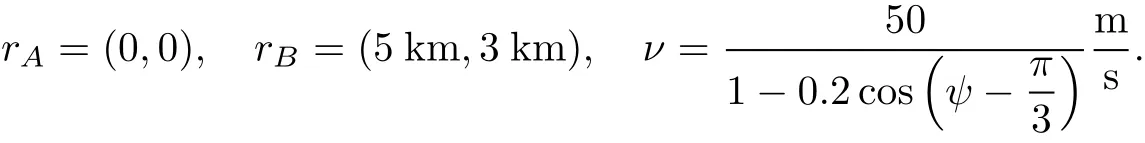
This problem was solved with the help of the controlimprovementalgorithm described in Subsection.To choose the initialapproximation itwas assumed thatthe helicopterflies straightthrough the point C,rC=(3 km, 2 km);flighttime is tACB=123 s.The optimum was reached in 3 iterations and almostcoincides with the evident optimal solution,that is straightflightfrom A to B with the maximal velocity and minimal transfer time tmin= 108 s.

6 Conclusion

In this paper,we introduce iterative procedures for improvement and optimization of discrete-time control systems.The algorithms are developed forboth free-end and constrained-end problems based on such nontraditional approaches as the extension principle,localization principle,and approximation of reachable set.Itis necessary to note that the proposed algorithms give the solution in the form of approximate linear synthesis of optimal control. The effectivenessofthe proposed algorithmsisdemonstrated through two examples,which justifiesfuture theoretical and experimentalresearch oftheirproperties.

Acknowledgments The authors would like to thank and express their appreciation to Prof.Dr.V.I.Gurman forhis kind advices and feedbacks on Section.

[1]Pontryagin L S,Boltianski V G,etal.Mathematicaltheory of optimalprocesses[M].New York:Interscience,1962.

[2]Bellman R.Dynamic programming[M].Princeton:Princeton University Press,1957.

[3]Krotov V F.Globalmethods in optimalcontroltheory[M].New York:Marcel Dekker,1996.

[4]PropoiA I.The maximum principle fordiscrete controlsystems[J].Automation and Remote Control,1966,26:1167-1177.

[5]Propoi A I.Elements of the theory of optimaldiscrete processes[M].Moscow:Nauka,1973.

[6]Boltyanskii V G.Optimalcontrolof discrete systems[M].Moscow:Nauka,1973.

[7]Evtushenko Yu G.Methods for solving extremal problems and their applications in optimization systems[M].Moscow: Nauka,1982.

[8]Gabasov R,Kirillova F M.Constructive optimization methods[M].Minsk:Universitetskoe,1984.

[9]Gorbunov V K.Reduction of optimalcontrolproblems to finite-dimensionalproblems[J].USSR Computational Mathematics and Mathematical Physics,1978,18(5):8–21.

[10]Pshenichny B N,Danilin Yu M.Numericalmethods in extremalproblems[M].Moscow:Mir Publishers,1982.

[11]Belyshev D V,Ukhin M Yu.Algorithm to determine the optimalcontrolof a discrete system[J].Automation and Remote Control,2005,66(8):1265-1273.

[12]Gurman V I.Theory of optimum discrete processes[J].Automation and Remote Control,1973,34(7):1082-1087.

[13]Rasina IV.Discretization ofcontinuous controllable systems based on generalized solutions[J].Automation and Remote Control,2011,72(6):1301-1308.

[14]Rasina IV.Iterative optimization algorithms fordiscrete-continuous processes[J].Automation and Remote Control,2012, 73(10):1591-1603.

[15]Gurman V I.The extension principle in control problems:general theory and learning examples[M].Moscow:Nauka, Fizmatlit,1998.

[16]Gurman V I,Ukhin M Yu.The extension principle in controlproblems:constructive methods and applied problems[M]. Moscow:Fizmatlit,2005.

[17]Fesko O V,Gurman V I,Rasina IV,et al.General schemes of iterative optimization with applications to optimalcontrol problems[J].Journalof the Operations Research Society of China,2016,4(2):223-232.

[18]Baturin V A,Goncharova E V.An improvement method based on an approximate description of attainability sets[J]. Automation and Remote Control,1999,60(11):1536-1544.

[19]Khrustalev MM.Exactdescription ofreachable sets and globaloptimality conditions fordynamic systems[J].Automation and Remote Control,1988,49(5):597-604.

[20]Gurman V I,Baturin V A,Rasina IV,et al.Approximate methods of optimal control[M].Irkutsk:Irkutsk University, 1983.

[21]Logsdon J S,Biegler L T.Accurate solution of differential-algebraic optimization problems[J].Chem Eng Sci,1989, 28:1628-1639.

[22]Dadebo S A,McAuley K A.Dynamic optimization of constrained chemical engineering problems using dynamic programming[J].Comput Chem Eng,1995,19:513-525.

[23]Rajesh J,Gupta K,Kusumakar H S,etal.Dynamic optimization of chemicalprocesses using antcolony framework[J]. Computers and Chemistry,2001,25:583-595.

[24]Cizniar M,Salhi D,Fiker M,etal.Dynopt–dynamic optimisation code for matlab[C].Proceedings of Technical Computing,2005.

[25]Fesko O.A parallelapproach to improvementand estimation of the approximate optimalcontrol[J].Journalof Computational Science,2012,3(6):486-491.

O 22 Document code:A Article ID:1000-5137(2017)03-0333-10 2010 MSC:93C55

10.3969/J.ISSN.100-5137.2017.03.001

date:2017-03-06

This research was supported by the Russian Foundation for Basic Research(15-01-01915 A,15-01-01923 A)and the National Science Foundation of China(11471118).

?Corresponding author:Ni Mingkang,professor,research area:applied mathematics,E-mail:xiaovikdo@163.com