LIU Xiu-sheng

(School of Mathematics and Physics,Hubei Polytechnic University,Huangshi 435003,China)

ON COMPLEMENTARY-DUAL CONSTACYCLIC CODES OVER Fp+vFp

LIU Xiu-sheng

(School of Mathematics and Physics,Hubei Polytechnic University,Huangshi 435003,China)

In this paper,we investigate the complementary-dual(1-2v)-constacyclic codes over the ring Fp+vFp(v2=v),where p is a prime.Using the decomposition C=vC1-v⊕(1-v)Cvof a(1-2v)-constacyclic code over Fp+vFp,we obtain generator polynomial of the complementarydual(1-2v)-constacyclic code C.Then by means of the Gray map from Fp+vFpto F2p,we show that Gray images of complementary-dual(1-2v)-constacyclic codes over Fp+vFpare complementarydual cyclic codes over Fp.

complementary-dual(1-2v)-constacyclic codes;cyclic codes;negacyclic codes; constacyclic codes;generator polynomials

1 Introduction

A linear code with a complementary-dual(an LCD code)was def i ned in[3]to be a linear code C whose dual code C⊥satisf i es C∩C⊥={0}.It was shown in[3]that asymptotically good LCD codes exist and those LCD codes have certain other attractive properties.Yang and Massy showed that the necessary and sufficient condition for a cyclic code of length n to be an LCD code is that the generator polynomial g(x)is self-reciprocal and all the monic irreducible factors of g(x)have the same multiplicity in g(x)and in xn-1(see[4]). In[9],Sendrier indicated that linear code with complementary-duals meet the asymptotic Gilbert-Varshamov bound.Emaeili and Yari discussed in[8]the complementary-dual QC codes,and provided a sufficient condition for an ρ-generator QC code C to be an LCD code, and a necessary and sufficient condition under which a given maximal 1-generator index-2 QC code C is LCD.

In recent years,Dinh established the algebrac structure in terms of polynomial generators of all repeated-root constacyclic codes of length 3ps,4ps,6psover Fpm.Using these structures,LCD codes were identif i ed among them(see[5-7]).

The purpose of this paper is to give the algebraic structure in terms of generator polynomials of all complementary-dual(1-2v)-constacyclic codes of length n over Fp+vFp. The necessary background materials on constacyclic codes and a Gray map are given in Section 2.In Section 3,we give the generator polynomials of the complementary-dual cyclic and negacyclic codes of length n=ptm over Fp,and show an enumeration formula for the complementary-dual cyclic and negacyclic codes of length n over Fp.In Section 4,Theorem 4.5 provides a necessary and sufficient condition under which a given(1-2v)-constacyclic code C of length n over Fp+vFpis an LCD.The generator polynomials and enumeration of(1-2v)-constacyclic codes length n over Fp+vFpare given by Theorem 4.7 under which C is an LCD code of length n over Fp+vFp.

2 Preliminaries

Throughout this paper,p is an odd prime,Fpis a fi nite fi eld with p elements.Let R be the commutative ring Fp+vFp={a+vb|a,b∈Fp}with v2=v.The ring R is a semi-local ring,it has two maximal ideals hvi={av|a∈Fp}and h1-vi={b(1-v)|b∈Fp}.It is easy to see that bothare isomorphic to Fp.From Chinese remainder theorem,we have R=hvi⊕h1-vi.We denote 1-2v byμfor simplicity.The following notations for codes over R are also valid for codes over Fp.A code of length n over R is a nonempty subset of Rn,and a code is linear over R if it is an R-submodule of Rn.Let x=(x0,x1,···,xn-1) and y=(y0,y1,···,yn-1)be any two elements of Rn,we de fi ne an inner product over R by x·y=x0y0+···+xn-1yn-1.If x·y=0,we say x and y are orthogonal.

The dual code C⊥of C is de fi ned by C⊥={x∈Rn|x·y=0 for all y∈C}.It is easy to verify that C⊥is always a linear code over R for any code C code over R.

Let C be a code of length n over R(or Fp)and P(C)be its polynomial representation, i.e.,

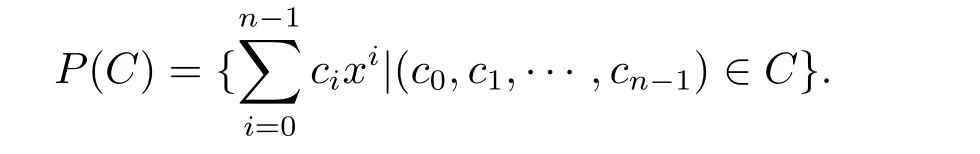
Let τ be map from Rnto Rngiven by τ(c0,c1,···cn-1)=(μcn-1,c0,···,cn-2).Then code C is said to beμ-constacyclic if τ(C)=C.

It is well known that a code C of length n over R(or Fp)is cyclic if and only if P(C)is an ideal of,a code C of length n over R(or Fp)is negacyclic if and only if P(C)is an ideal o,a code C of length n over R isμ-constacyclic if and only if P(C)is an ideal of

Now we give the de fi nition of the Gray map on Rn.Observe that any element c∈R can be expressed as c=a+vb,where a,b∈Fp.The Gray map Φ：R→Fp2is given byΦ(c)=(-b,2a+b).This map can be extended to Rnin a natrual way：

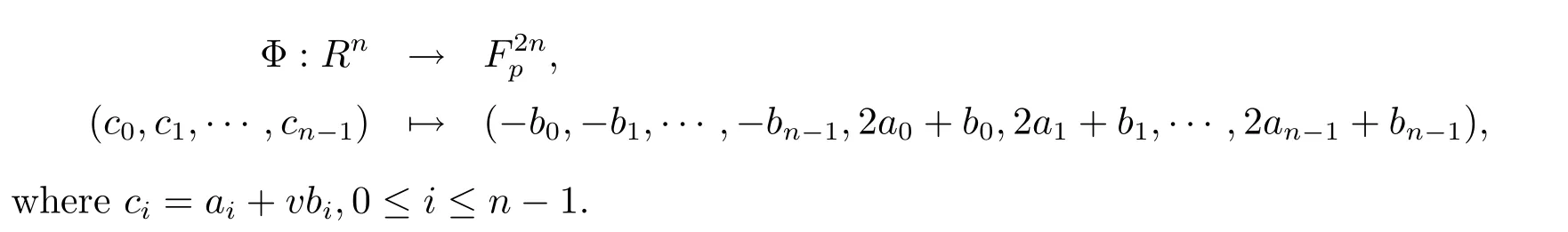
A code C is a complementary-dual cyclic(or negacyclic)code of length n over R(or Fp)if it is a cyclic(or negacyclic)and LCD code of length n over R(or Fp),and a code C is a complementary-dualμ-constacyclic code of length n over R if it is aμ-constacyclic and LCD code of length n over R.

3 Generator Polynomials of the Complementary-Dual Cyclic Codes over Fp

We begin with two concepts.

Proposition 3.1If C is a cyclic(or negacyclic)code of length n over Fp,then the dual C⊥of C is ann?(C).

Suppose that f(x)is a monic(i.e.,leading coefficient 1)polynomial of degree k with f(0)=c 6=0.Then by monic reciprocal polynomial of f(x)we mean the polynomialf?(x)= c-1f?(x).We recall a result about LCD codes which can be found in[5].

Proposition 3.2If g1(x)is the generator polynomial of a cyclic code C of length n over Fp,then C is an LCD code if and only if g1(x)is self-reciprocal(i.e.,?g1(x)=g1(x))and all the monic irreducible factors of g1(x)have the same multiplicity in g1(x)and in xn-1.

Similar to the discussions in[5],we have the following proposition.

Proposition 3.3If g2(x)is the generator polynomial of a negacyclic code C of length n over Fp,then C is an LCD code if and only if g2(x)is self-reciprocal(i.e.,?g2(x)=g2(x)) and all the monic irreducible factors of g2(x)have the same multiplicity in g2(x)and in xn+1.

We fi rst investigate the generator polynomials of the complementary-dual cyclic codes over Fp.

It is well known that each cyclic code over Fpis uniquely determined by its generator polynomial,a monic divisor of xn-1 over Fp.In order to describe the generator polynomialsof the complementary-dual cyclic codes,we need to know the factorization of the polynomial xn-1 over Fp.Write n=ptm,where t is a nonnegative integer depending on n and gcd(m,p)=1.Then xn-1=(xm-1)pt.

For any irreducible polynomial dividing xm-1 over Fp,its reciprocal polynomial also divides xm-1 over Fpand is also irreducible over Fp.Since gcd(m,p)=1,the polynomial xm-1 factors completely into irreducible factors in Fp[x]as

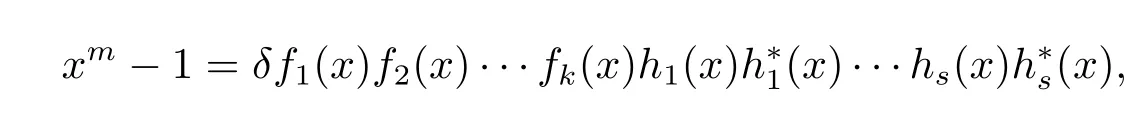
where δ 6=0 in Fp,f1(x),f2(x),···,fk(x)are irreducible polynomials that are associates to their own reciprocals,and h1(x),h?1(x);···;hs(x),h?s(x)are pairs of mutually reciprocal irreducible polynomials.Therefore

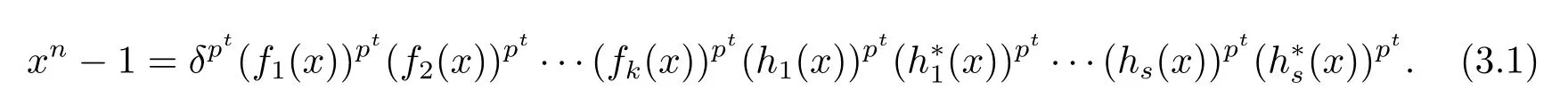
We can describe the generator polynomials of the complementary-dual cyclic codes as soon as we know the factorization of xn-1 over Fp.

Theorem 3.4Let xn-1 be factorized as in(3.1).A cyclic code C of length n over Fpis an LCD code if and only if its generator polynomial is of the form

where αi∈{0,pt}for each 1≤i≤k,and βj∈{0,pt}for each 1≤j≤s.

Proof Let C be a cyclic code of length n over Fp,and let g(x)be its generator polynomial.We need to show that C is an LCD code if and only if g(x)is of the form as in (3.2).

Suppose that

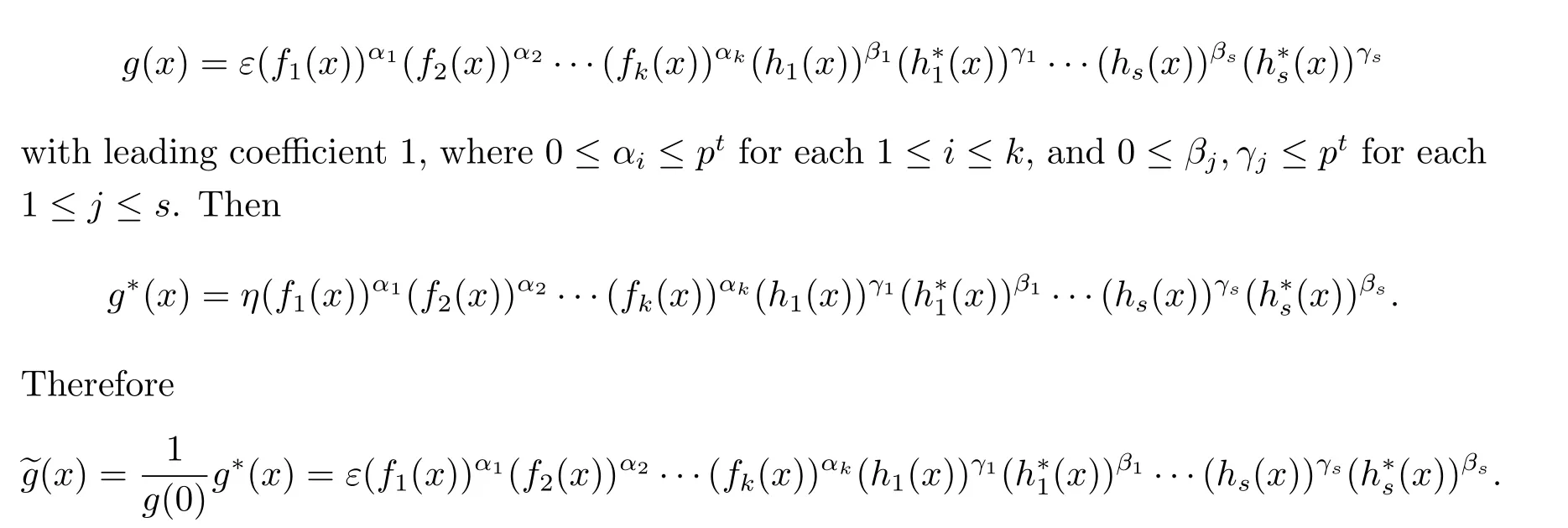
By Proposition 3.2,C is an LCD code if and only if g(x)=?g(x)and all the monic irreducible factors of g(x)have the same multiplicity in g(x)and in xn-1,i.e.,βj=γjfor each 1≤j≤s,αi∈{0,pt}for each 1≤i≤k,and βj∈{0,pt}for each 1≤j≤s.

Therefore,C is an LCD code if and only if its generator polynomial g(x)is of the form as in(3.2).

The following corollary is obvious.

Corollary 3.5Let xn-1 be factorized as in(3.1).Then the number of nontrivial complementary-dual cyclic codes is exactly 2k+s-2.

Now we discuss the complementary-dual negacyclic codes.

Since n=ptm,gcd(m,p)=1,we have xn+1=.For any irreducible polynomial dividing xm+1 over Fp,its reciprocal polynomial also divides xm+1 over Fpand is also irreducible over Fp.Since gcd(m,p)=1,the polynomial xm+1 factors completely into irreducible factors in Fp[x]as

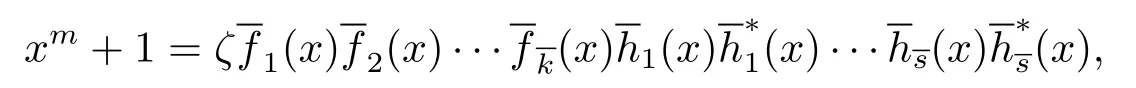
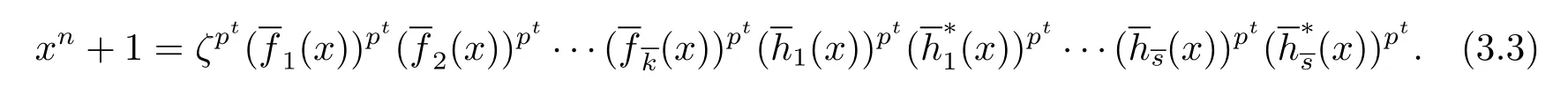
In light of Proposition 3.3 and(3.3),the following theorem is easy to vertify.

Theorem 3.6Let xn+1 be factorized as in(3.3).A negacyclic code C of length n is LCD code if and only if its generator polynomial is of the form

Obviously,C=0 and C=Fpnare complementary-dual negacyclic codes,which are called the trivial complementary-dual negacyclic codes over Fp.The following corollary is easy to obtain.

Corollary 3.7Let xn+1 be factorized as in(3.3).Then the number of nontrivial complementary-dual cyclic codes is exactly

4 Generator Polynomials of Complementary-Dualμ-Constacyclic Codes over R

Let C1,C2be codes over R.We denote C1⊕C2={a+b|a∈C1,b∈C2}.For a code C over R,let us take

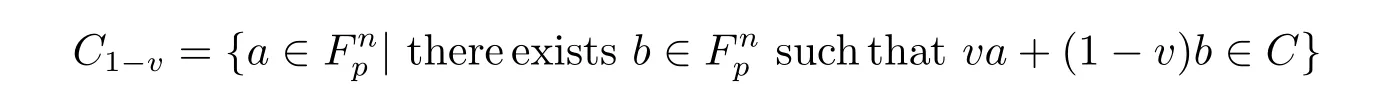
and

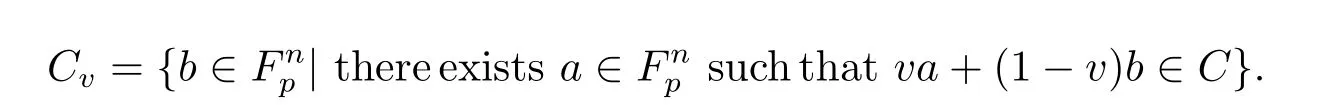
The following four lemmas can be found in[1].

Lemma 4.1 Let C=vC1-v⊕(1-v)Cvbe a linear code of length n over R.Then C is aμ-constacyclic code length n over R if and only if C1-vand Cvare negacyclic and cyclic codes of length n over Fp,respectively.

Lemma 4.2 If C=vC1-v⊕(1-v)Cvis aμ-constacyclic code of length n over R,then there is a unique polynomial g(x)=vg1(x)+(1-v)g2(x)such that C=hg(x)i,g(x)|xn-μ, and|C|=where g1(x)and g2(x)are the generator polynomials of C1-vand Cvover Fp,respectively.

Lemma 4.3 Let C=vC1-v⊕(1-v)Cvbe aμ-constacyclic code length n over R,and C=hvg1(x)+(1-v)g2(x)i,where g1(x)and g2(x)are the generator polynomials of C1-vand Cvover Fp,respectively.Then Φ(C)=hg1(x)g2(x)i,and Φ(C⊥)=Φ(C)⊥.

Lemma 4.4 Let C=vC1-v⊕(1-v)Cvbe aμ-constacyclic code length n over R.Then its dual code C⊥is also aμ-constacyclic code length n over R,and

Theorem 4.5 Let C=vC1-v⊕(1-v)Cv=hvg1(x)+(1-v)g2(x)i be aμ-constacyclic code of length n over R.Then C is an LCD code of length n over R if and only if C1-vand Cvare the complementary-dual negacyclic and cyclic codes of length n over Fp,respectively.

Proof By Lemma 4.4,we know that C∩C⊥={0}if and only if C1-v∩C1⊥-v={0}, and Cv=

Form the above proof,the following corollary can be obtained at once.

Corollary 4.6Let C=vC1-v⊕(1-v)Cvbe aμ-constacyclic code of length n over R.Then C is an LCD code of length n over R if and only if Φ(C)is a complementary-dual cyclic codes of length 2n over Fp.

Proof By Lemma 4.1 and Lemma 4.3,we have C1-v=hg1(x)i,and Cv=hg2(x)i.

Since C1-vis a complementary-dual negacyclic code,g1(x)=?g1(x)and all the monic irreducible factors of g1(x)have the same multiplicity in g1(x)and in xn+1.

Similarly,g2(x)=?g2(x)and all the monic irreducible factors of g2(x)have the same multiplicity in g2(x)and in xn-1.

In light of Lemma 4.2,Φ(C)=hg1(x)g2(x)i.Write g(x)=g1(x)g2(x).Then

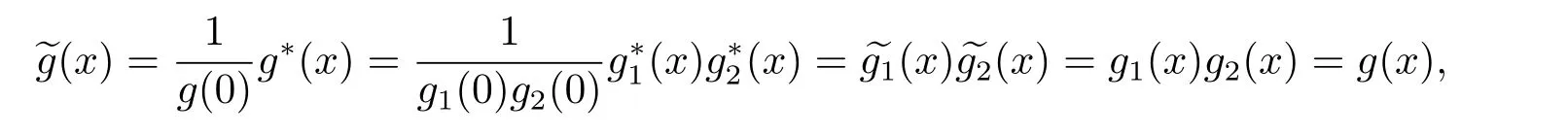
which implies that?g(x)is self-reciprocal.

Let xn+1=g1(x)h1(x),and xn-1=g2(x)h2(x).Then

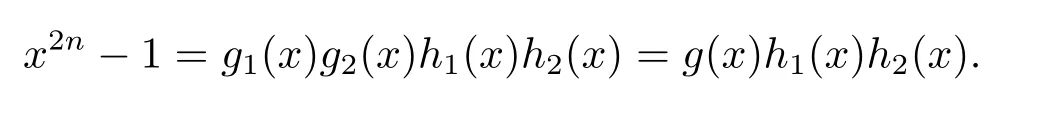
Therefore all the monic irreducible factors of g(x)have same multiplicity in g(x)have the same multiplicity in g(x)in x2n-1.

We summarize the above fact to conclude that Φ(C)is a complementary-dual cyclic code of length 2n over Fp.

Conversely,if α∈C∩C⊥,i.e.,α∈C,and α∈C⊥,then Φ(α)∈Φ(C),and Φ(α)∈Φ(C⊥)=Φ(C)⊥.Therefore Φ(α)∈Φ(C)∩Φ(C)⊥={0},i.e.,Φ(α)=0.It is implies thatα=0 since Φ is bijective from RntoHence C∩C⊥={0},i.e.,C is a complementarydual cyclic code of length n over R.

By Theorem 3.5,Theorem 3.7,Corollary 3.6 and Corollary 3.8,we get the following statements.

Theorem 4.7Let C=vC1-v⊕(1-v)Cvbe aμ-constacyclic code of length n over R,xn-1 and xn+1 be factorized as in(3.2)and(3.3),respectively.Then

(1)C is an LCD code of length n over R if and only if its generator polynomial is of the form

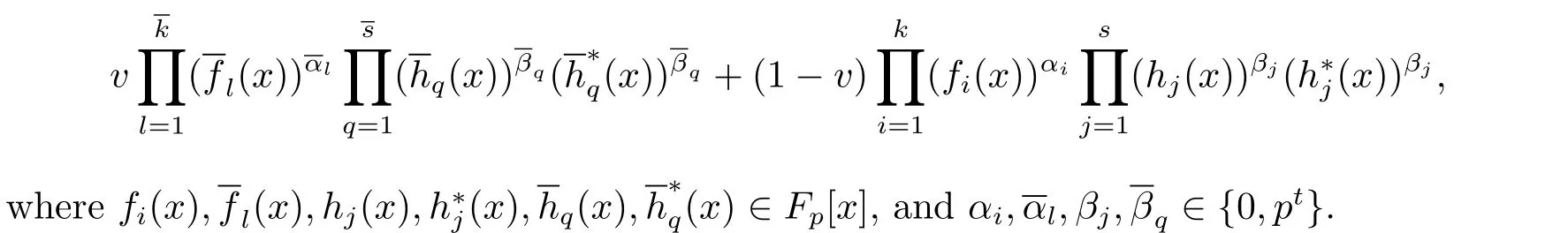
(2)Φ(C)is an LCD code of length 2n over Fpif and only if its generator polynomial is of the form

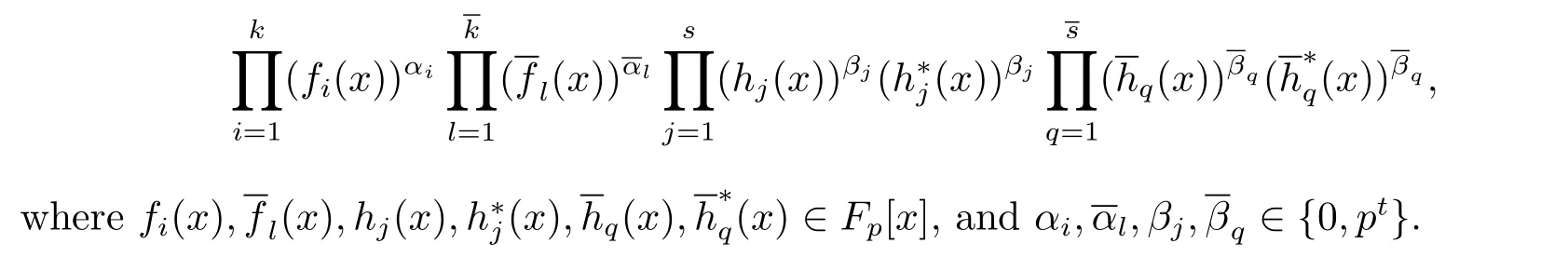
(3)The number of nontrivial complementary-dualμ-constacyclic codes of length n over R is exactly

Now,we give the following two examples to illustrate the above results.

Example 1In F5[x],

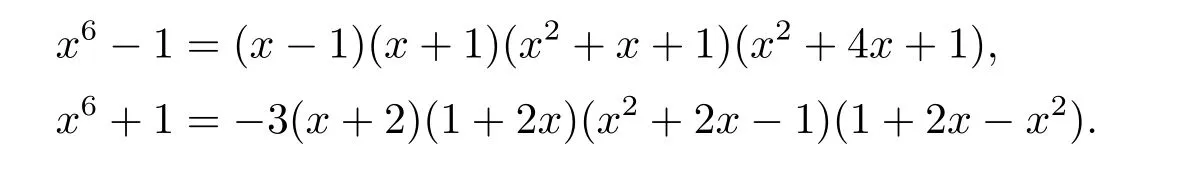
Observe that the polynomials x-1,x+1,x2+x+1,and x2+4x+1 are irreducible polynomials that are associates to their own reciprocals,and x+2,1+2x;x2+2x-1,1+2x-x2are two pairs of mutually reciprocal irreducible polynomials over F5.There are 62 nontrivial complementary-dualμ-constacyclic codes of length 6 over R=F5+vF5,i.e.,

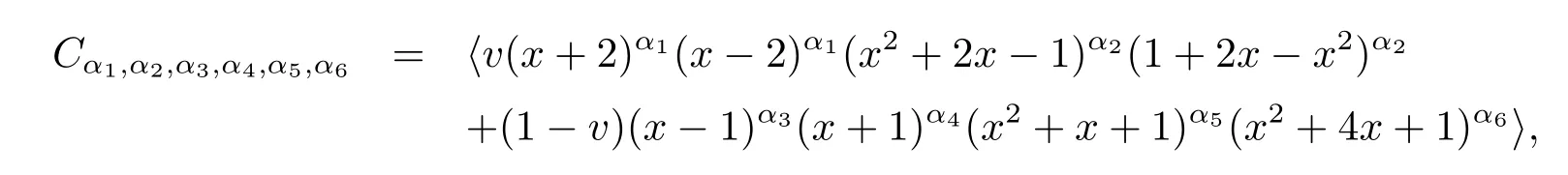
where αi∈{0,1}for 1≤i≤6,and(α1,α2,α3,α4,α5,α6)6=(0,0,0,0,0,0),(1,1,1,1,1,1).

Now we list some optimal codes obtained from complementary-dualμ-constacyclic codes over R=F5+vF5in Table 1.

Example 2In F7[x],

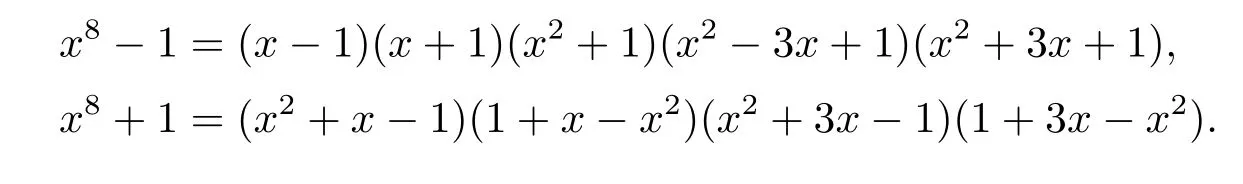
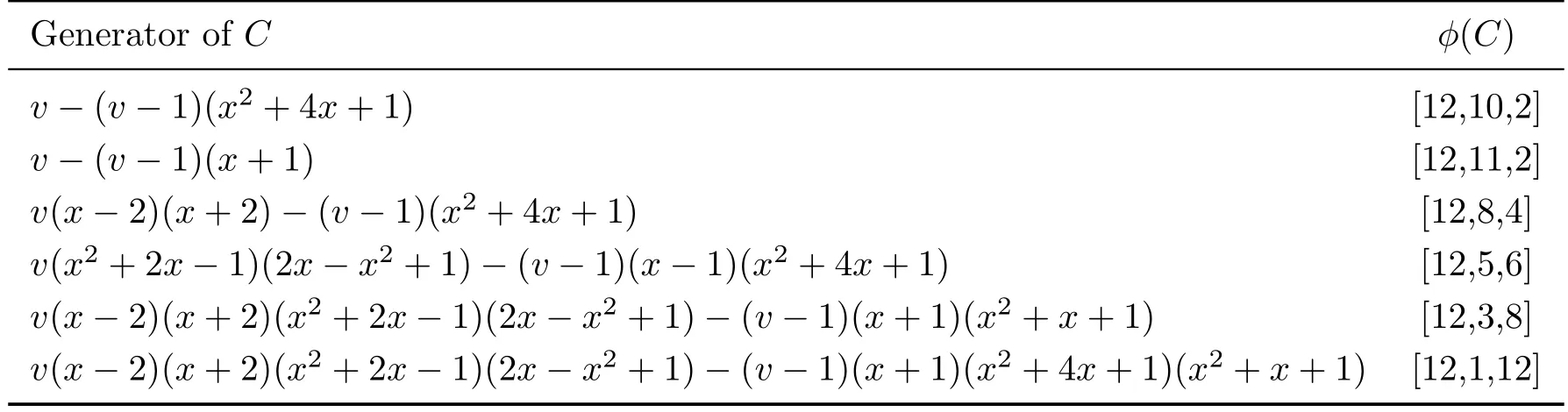
Table 1：Optimal codes of length 12 overF5from complementary-dualμ-constacyclic codes over R=F5+vF5

Observe that the polynomials x-1,x+1,x2+1,x2-3x+1,and x2+3x+1 are irreducible polynomials that are associates to their own reciprocals,and x2+x-1,1+x-x2;x2+3x-1,1+3x-x2are two pairs of mutually reciprocal irreducible polynomials over F7.There are 126 nontrivial complementary-dualμ-constacyclic codes of length 8 over R=F7+vF7, i.e.,

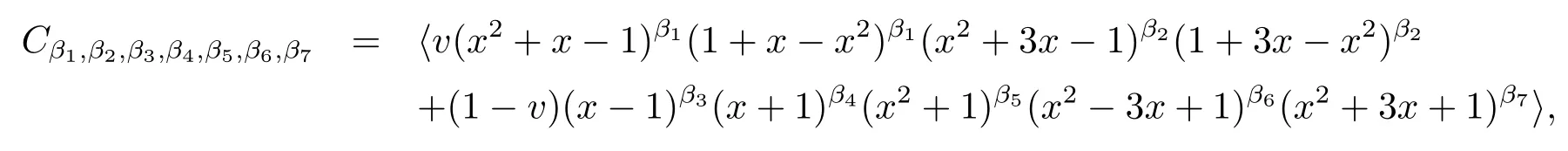
where βj∈{0,1}for 1≤j≤7,and

Now we list some optimal linear codes obtained from complementary-dualμ-constacyclic codes over R=F7+vF7in Table 2.

Table 2：Optimal codes of length 16 overF7from complementary-dualμ-constacyclic codes over R=F7+vF7

[1]Zhu S,Wang L.A class of constacyclic ocdes over Fp+vFpand its Gray image[J].Disc.Math., 2011,311：677-2682.

[2]Bakshi G K,Raka M.Self-dual and self-orthogonal negacyclic codes of length 2psover a fi nite if eld[J].Finite Field Appl.,2013,19：39-54.

[3]Massey J L.Linear codes with complementary duals[J].Disc.Math.,1992,106/107：337-342.

[4]Yang X,Massey J L.The condition for a cyclic code to have a complementary dual[J].Disc.Math., 1994,126：391-393.

[5]Dinh H Q.Structure of repeated-root constacyclic codes of length 3psand their duals[J].Disc. Math.,2013,313：983-991.

[6]Dinh H Q.On repeated-root constacyclic codes of length 4ps[J].Asian-European J.Math.,2010,1：1-25.

[7]Dinh H Q.Repeated-root cyclic codes of length 6ps[J].MAS Contem.Math.,2014,609：69-87.

[8]Esmaeili M,Yari S.On complementary-dual quasi-cyclic codes[J].Finite Field Appl.,2009,15：357-386.

[9]Sendrier N.Linear codes with complementary duals meet the Gilbert-Varshamov bound[J].Discrete Math.,2004,304：345-347.

[10]Hu ff man W C,Pless V.Fundamentals of error-correcting codes[M].Cambridge：Cambridge University Press,2003.

環(huán)Fp+vFp上互補(bǔ)對(duì)偶常循環(huán)碼

劉修生

(湖北理工學(xué)院數(shù)理學(xué)院,湖北黃石435003)

本文研究了環(huán)Fp+vFp上互補(bǔ)對(duì)偶(1-2v)-常循環(huán)碼.利用環(huán)Fp+vFp上(1-2v)-常循環(huán)碼的分解式C=vC1-v⊕(1-v)Cv,得到了環(huán)Fp+vFp上互補(bǔ)對(duì)偶(1-2v)-常循環(huán)碼的生成多項(xiàng)式.然后借助從Fp+vFp到F2p的Gray映射,證明了環(huán)Fp+vFp上互補(bǔ)對(duì)偶(1-2v)-常循環(huán)碼的Gray像是Fp的互補(bǔ)對(duì)偶循環(huán)碼.

互補(bǔ)對(duì)偶(1-2v)-常循環(huán)碼;循環(huán)碼;負(fù)循環(huán)碼;常循環(huán)碼;生成多項(xiàng)式

O157.4

A

0255-7797(2017)05-0916-09

?Received date：2016-04-07Accepted date：2016-09-05

Supported by Scientif i c Research Foundation of Hubei Provincial Education Department of China(D20144401)and the National Science Foundation of Hubei Polytechnic University of China(12xjz14A).

Biography：Liu Xiusheng(1960-),male,born at Daye,Hubei,professor,major in groups and algebraic coding,multiple linear algebra.

2010 MR Subject Classif i cation：94B05;94B15;11T71