R.Daneshmand and M.K.TavassolyAtomic and Molecular Group,Faculty of Physics,Yazd University,Yazd,Iran

2Photonics Research Group,Engineering Research Center,Yazd University,Yazd,Iran

3The Laboratory of Quantum Information Processing,Yazd University,Yazd,Iran

1 Introduction

The problem of quantization and then description of quantum behavior of electromagnetic waves in empty cavities has been appropriately solved.[1]But,by developing optical devices,the light propagation may be taken place in media that their characteristic parameters differ from the empty space.For instance,it is necessary to study the light propagation in conductive media,i.e.,the media in which the conductivity is not zero.In order to study the time behavior of nonclassical properties of light in this media,it is important to quantize the propagating radiation field.Considering the constant values for conductivity and permittivity parameters of media results in the timedependent Hamiltonian,[2?3]which is known as Caldirola–Kanai(CK)Hamiltonian.[4?6]This Hamiltonian can appropriately describe the dynamics of a harmonic oscillator which undergoes dissipation.[7?8]Moreover,the timedependency of this Hamiltonian makes rigorous complexity in quantization and evaluation of the corresponding nonclassical properties of propagating light.One of the useful methods to overcome this complexity is the timeinvariant operator method which has been introduced by Lewis and Riesenfeld[9]known as LR method.

Recently,the quantum description of electromagnetic waves propagating in conductive media has been studied using the LR method,[10?11]and the generalized annihilation and creation operators of the corresponding light have been derived.The obtained generalized operators may be rewritten in terms of the standard bosonic annihilation and creation operators of the simple harmonic oscillator which is known as Bogoliubov transformations.[12]For this reason,it is concluded that the eigenstates of generalized annihilation operator are the well-known squeezed states with eigenvalue zero.[10?11,13]

In this respect,as the first aim of this paper,after a brief review on the quantization of electromagnetic waves in conducting media,we introduce the explicit form of the eigenstates of generalized annihilation operator associated with the light which is propagated in conducting media.As will be seen,such states are indeed the time-and conductivity-dependent squeezed states.To this end,two different states are obtained,one involving even number states(squeezed vacuum states[14])and the other involving odd number states(one-photon squeezed states[15]).We call these states as time-and conductivity-dependent even(TCDE)squeezed states and time-and conductivitydependent odd(TCDO)squeezed states,respectively.Also,the superposition of TCDE/O squeezed states are taken into account.After that,the nonclassical properties of the introduced states,such as sub-Poissonian statistics,quadrature squeezing as well as quasi-distribution functions(Husimi and Wigner functions)are evaluated,numerically.Then,the time behavior and the effect of conductivity on the dynamics of these nonclassicality criteriaare studied.

In addition,developing the new states of light,[16?17]it is important to study the nonclassical properties of these states and their superpositions.[18?20]For instance,even and odd coherent states[21?23]present high nonclassical properties.[24?25]Also,the generalization of even and odd coherent states attracted much attention.[26?28]Recently,in Ref.[29],two new classes of these states as excited even/odd coherent states have been defined which are obtained by repeated action of the creation operator to the even/odd coherent states.As the last aim of this paper,the generalized time-dependent creation operator which is derived in the quantization of electromagnetic waves in conducting media is applied to the standard even/odd coherent states.After arriving at the explicit form of these time-dependent states which we call them time-and conductivity-dependent excited even/odd(TCDEE/O)coherent states,the assessment of the nonclassical behavior of the obtained state over time is numerically established.In this respect,we calculate the Mandel parameter and Wigner distribution function,by which the sub-Poissonian statistics and nonclassicality of the states are shown,respectively.

The rest of this paper is organized as follows:In the next section,we present a brief review on the quantization of electromagnetic waves in conducting media.In Sec.3,making use of the time-dependent annihilation operator obtained in the last section,the TCDE/O squeezed states and their superpositions are derived,and their nonclassical properties are evaluated.In Sec.4,the TCDEE/O coherent states are obtained and the dynamics of corresponding nonclassical properties of these states are studied.Finally,in Sec.5 the summary and concluding remarks are presented.

2 A Brief Review on the Quantization of Electromagnetic Waves in Conducting Media

Let us consider the system in Refs.[10–11],consisting of the electromagnetic wave in a certain volume of space ful filled by a conducting media with the characteristic parameters,?(t)as electric permittivity,μ(t)as magnetic permeability andσ(t)as conductivity of the media.If one restricts himself to the case in which the above parameters are real,this consideration can be understood as a damped system,which can be described by CK Hamiltonian.Making use of the Coulomb gauge and Maxwell’s equations,it is found that the vector potential→Asatisfies the following wave equation

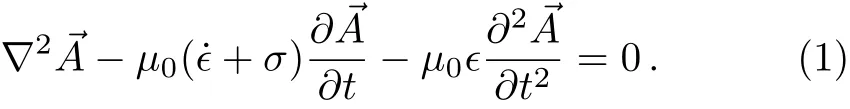
Expanding the general form of vector potential in terms of the modewith amplitudeql(t),i.e.,and substituting the latter relation into the wave equation(1),we are led to

Here,?l(t)=c(t)ωl/c0is the modi fied frequency,whereis the velocity of electromagnetic wave in the time-depending media.The velocity of electromagnetic wave in the vacuum is indicated byc0.It is easy to understand that Eq.(2)represents an equation of motion with dissipation due to the first order derivation ofqlwith respect to time.Now,and in direct relation to our presentation,it is found that the above-mentioned equation of motion can also be derived directly from the classical Hamiltonian

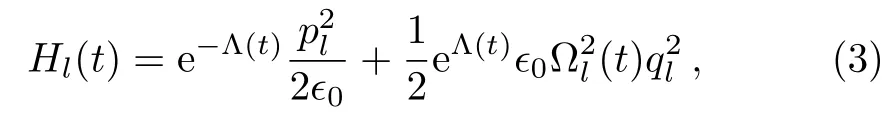
whereqlandplare canonical conjugate variables and

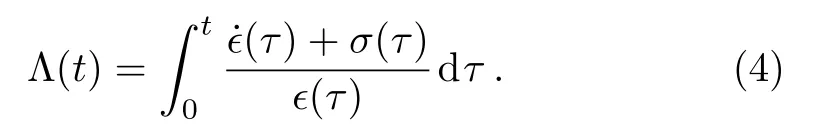
Considering constant values for electric permittivity i.e.,?(t)=?0andσ(t)=σ0,one has ?l(t)=ωland Λ(t)=λtwithλ=σ0/?0.Therefore,the Hamiltonian in Eq.(5)reduces to the well-known CK Hamiltonian for a singlemode electromagnetic field,which is defined as

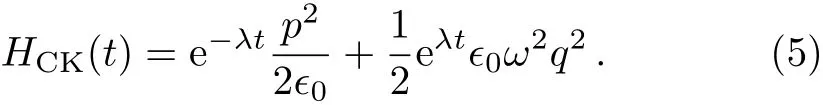
In order to discuss the quantum treatment of the considered system,it is necessary to find the eigenvalues of the quantized Hamiltonian in Eq.(5).Whereas this Hamiltonian is time-dependent and the separation of time variables from others is impossible,an alternative method has been used.In this situation the time-invariant operator method known as LR method[9]is employed.In this method,it is attempted to find a hermitian operator,which satisfies the Liouville-von Neumann equation

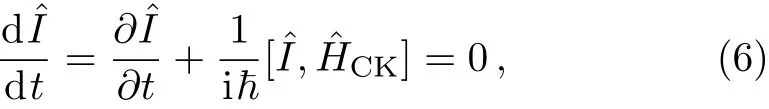
with the solution

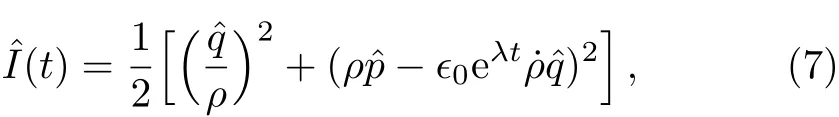
in which the time-dependent functionρ(t)can be derived from the following equation

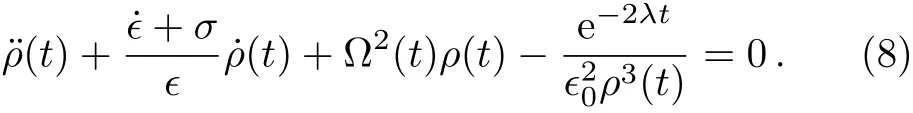
One of the possible solutions satisfying the above equation iswithConsequently,by introducing the generalized annihilation and creation operators of the form it is shown that the invariant operator can be rewritten asNoticing that,the explicit form ofρ(t)(and so(t))is known,therefore,the explicit forms ofA,A?in terms of the operators,can be determined.Considering the standard bosonic annihilation and creation operators,the generalized annihilation and creation operators may be rewritten as

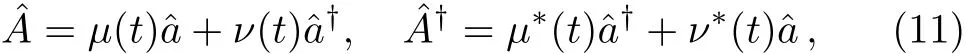
which are known as the Bogoliubov transformations,where

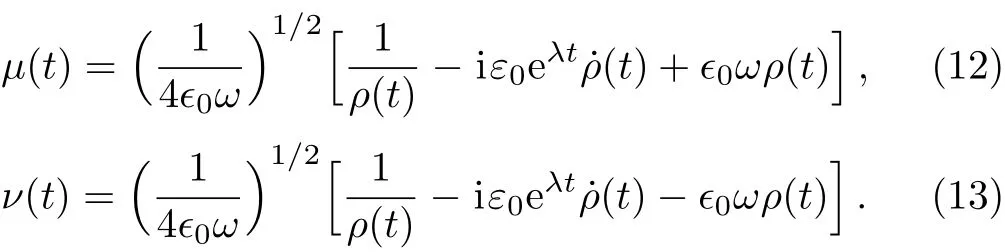
The task of the next section is to find the timedependent eigenstates based on Eqs.(11)–(13)and evaluating the temporal behavior of the associated nonclassical properties and also,the effect of conductivity parameter on them.

After that,in Sec.4,Eqs.(11)–(13)are also utilized to obtain the explicit form of the TCDEE/O coherent states and evaluate their nonclassical characteristics and also,the in fluence of conductivity parameter on them.

3 Time-and Conductivity-Dependent Even/Odd(TCDE/O)Squeezed States

Based on what is previously argued,a squeezed state|ξ〉may be defined as the eigenstate of the operatorwith eigenvalue zero.In this respect,we continue to find the solution of the eigenvalue equation Considering the squeezed state as the superposition of number states,i.e.,based on Eq.(14)we are led to the following recursion relation

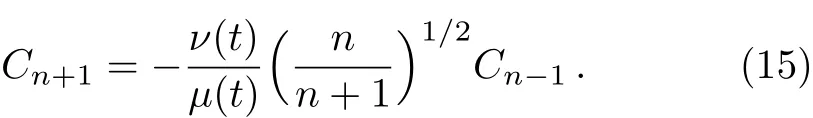
In this way,two distinct solutions may be obtained from the above equation,one involving only even number states,which we call time-and conductivity dependent even(TCDE)squeezed states

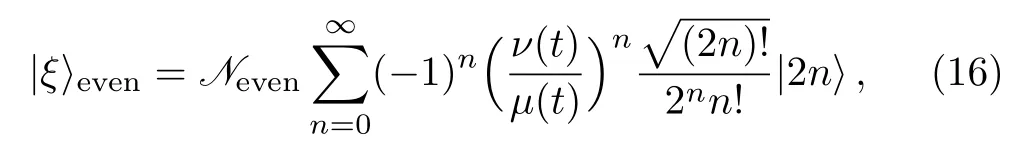
with normalization factor

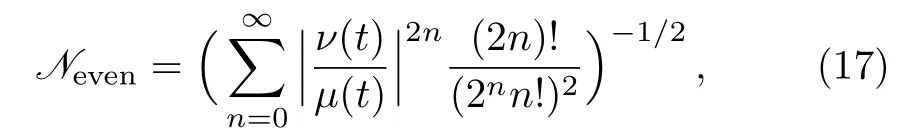
and the other one only involves odd number states,which we call time-and conductivity-dependent odd(TCDO)squeezed state

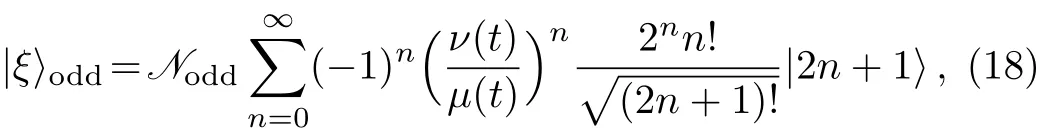
with the normalization factor

The probability of detecting 2nphotons in the field is expressed asP2n=|〈2n|ξ〉even|2and similarly,for detecting 2n+1 photons asP2n+1=|〈2n+1|ξ〉odd|2.In Fig.1,the variation of photon number distributions(i.e.,P2n,P2n+1)in different times for the conductivity valueσ0=0.5 is displayed.??It is worth mentioning that we should use histogram to correctly represent number distribution against the photon number,which is integer.However,due to our purpose to compare the effect of different values of conductivity parameters,we use continuous lines.So,the values of the plots in Figs.1 and 2 are valid only for integer values of n.Also,in Fig.2,the variation ofP2nandP2n+1,by considering the constant timet=3 and different values ofσ0is depicted.The oscillatory behavior of the number distribution function is one of the nonclassicality features of the obtained states.

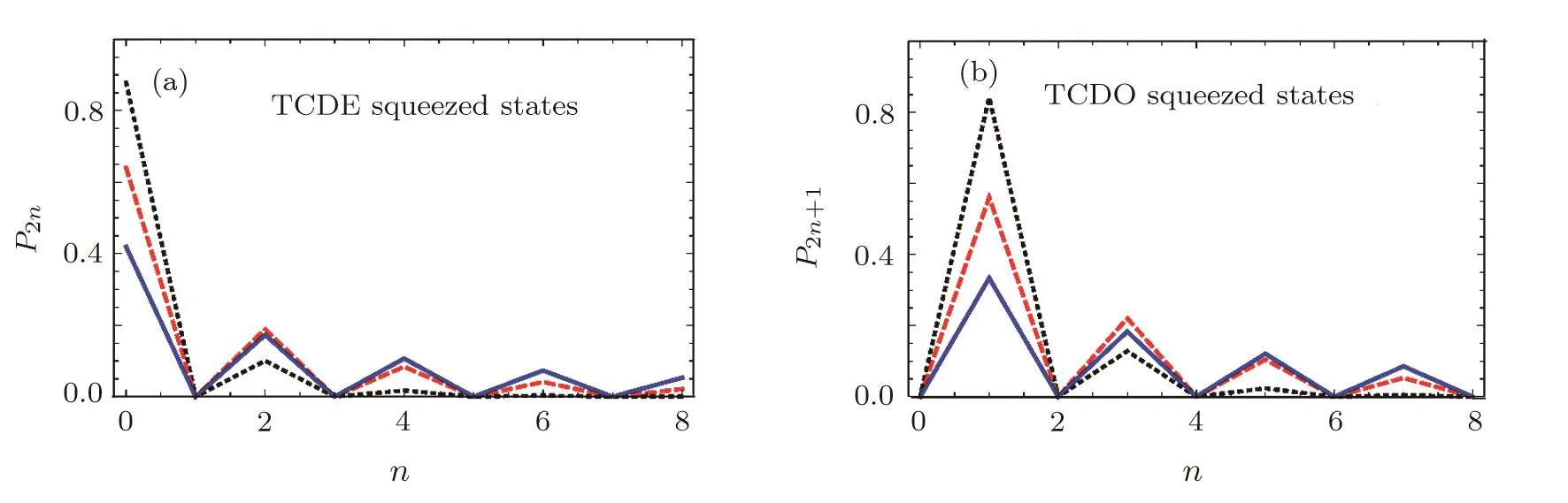
Fig.1 (Color online)Photon number distribution,for(a)TCDE and(b)TCDO squeezed states with σ0=0.5 at scaled times t=2(dotted black line),t=4(dashed red line)and t=6(continues blue line).Other chosen values are as ?0= ω = ? =1.

Fig.2 (Color online)Photon number distribution,for(a)TCDE and(b)TCDO squeezed states with scaled time t=6 for σ0=0.2(dotted black line),σ0=0.4(dashed red line)and σ0=0.6(continues blue line).Other chosen values are as Fig.1.

Also,it is possible to define the superposition of the TCDE/O squeezed states,i.e.,

where|ξ〉even,|ξ〉oddare obtained in Eqs.(16)and(18).

We end this part with a discussion on the relation between the two approaches for the construction of squeezed states.As is seen,in above we have used the eigenvalue equation(Eq.(14))to produce the squeezed field state.However a question may naturally be arisen:What is the relation between the above states and the squeezed state,which is constructed by the action of the squeezed operator on the vacuum state?In this regard,the following squeezing operator has been defined[31?32]

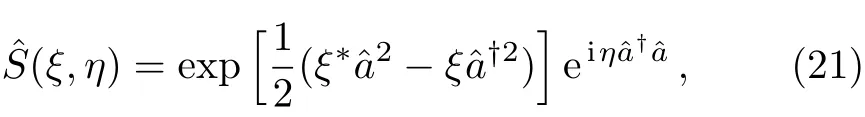
whereξ=|ξ|ei?,in which phases?,η∈Rand|ξ|≥ 0.Therefore,we can introduce the squeezing parameterξand phase factorηin Eq.(21)in which the following operators can be obtained

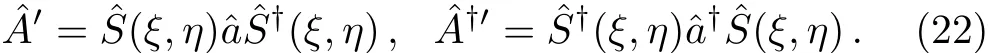
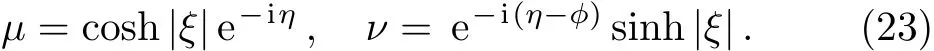
Based on the latter relations and the explicit forms ofμ(t)andν(t)respectively in Eqs.(12)and(13),we arrive at the exact form of the following time-dependent parameters:

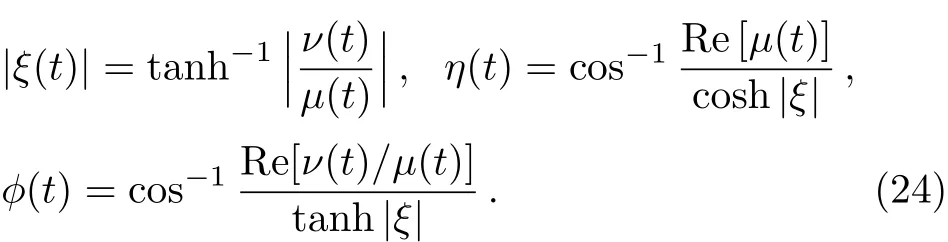
3.1 Nonclassical Properties of the Introduced States

To investigate the temporal behavior of the nonclassical properties for the introduced squeezed states in Eqs.(16),(18),and(20),we can utilize different criteria.In this section,we employ MandelQ-parameter as the representative of sub-Poissonian statistics as well as quadrature squeezing.Also,two quasi-distribution functions i.e.,Husimi(Q(α,α?))and Wigner(W(α,α?))functions are calculated.It ought to be mentioned that the employed parameters,which are constant in the whole of the rest of paper are as?0=ω= ? =1.

(i)Sub-Poissonian statistics

The Mandel parameter as a measure for recognition of the fact that how much a quantum state shows sub-Poissonian statistics is defined as

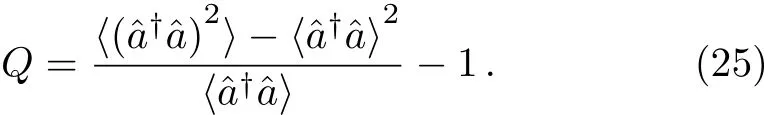
Thenegativity ofparameterQindicatesthesub-Poissonian statistics of a considered state as a nonclassical property.In Fig.3,the time behavior of this parameter corresponding to the TCDE squeezed state,TCDO squeezed state and the superposition of these states is displayed via considering three different values of conductivity(i.e.,σ0=0.1,0.3,and 0.9).Figure 3(a)is related to the TCDE squeezed state(i.e.,Eq.(16)).It is seen that,the curve of Mandel parameter is lied completely in positive region.In Fig.3(b),which is related to TCDO squeezed states in Eq.(18),the curve of Mandel parameter begins from the negative region and enters to the positive region by increasing time.It is deduced that the TCDO squeezed states with chosen values ofσ0,show the sub-Poissonian statistics at early times.Also,it is seen that by choosing the larger values for conductivity,the negativity and so this nonclassicality sign vanishes much sooner.Considering the third row of Fig.3(c),it is seen that the Mandel parameter for the superposition of TCDE and TCDO squeezed states(i.e.,Eq.(20))possesses negative values at early times similar to the case of TCDO squeezed states.But,for the case of superposition states,the negativity vanishes sooner than the TCDO squeezed states.

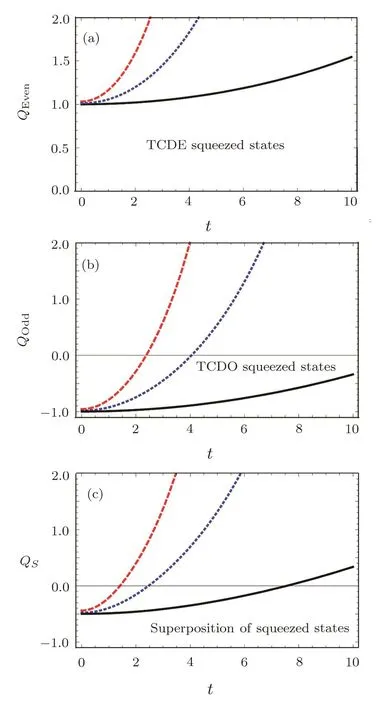
Fig.3 (Color online)TCDE squeezed states TCDO squeezed states Superposition of squeezed states.Dynamical behavior of Mandel parameter versus scaled time for TCDE,TCDO and the superposition of squeezed states,with σ0=0.1(continues black line), σ0=0.3(dotted blue line),and σ0=0.5(dashed red line).

(ii)Quadrature Squeezing

To study the quadrature squeezing,we consider two Hermitian operatorsThe quadrature squeezing parameter is then defined based on the variances of position(Δx)2and momentum(Δp)2asSxi=2(Δxi)2? 1 withxi=x,p.Subsequently,a state is squeezed inxidirection,when the inequality?1＜Sxi＜0 holds. Figure 4 shows the time behavior of the quadrature squeezing along thex-direction corresponding to the TCDE squeezed states,TCDO squeezed states and the superposition of these states,which is displayed for three different values of conductivity parameter(i.e.,σ0=0.1,0.3,and 0.9).According to these plots,one can clearly see that,this type of squeezing occurs for all desired states,specially for the TCDE squeezed states(Fig.4(a)).In the case of other two types of states(Figs.4(b)and 4(c)),the squeezing parameter is initially in the positive region and by increasing time enters the negative region.It should be emphasized on the interesting result that the squeezing parameter,eventually takes its most possibly negative value(?1)and this situation is preserved as time goes on.

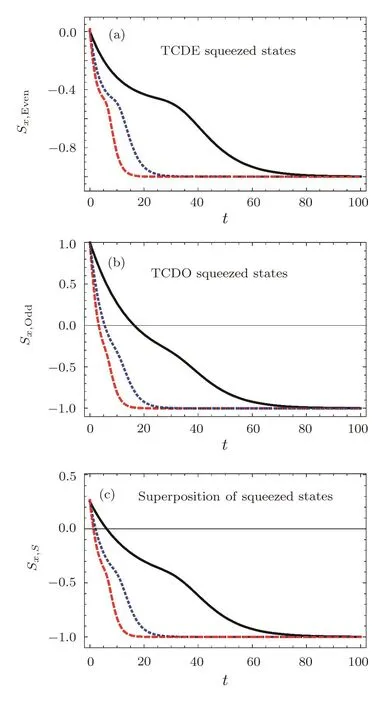
Fig.4 (Color online)TCDE squeezed states TCDO squeezed states Superposition of squeezed states Dynamical behavior of quadrature squeezing in x-direction versus scaled time for TCDE,TCDO squeezed states and their superpositions,with σ0=0.1(continues black line),σ0=0.3(dotted blue line),and σ0=0.5(dashed red line).

Therefore,for enough large time such states are fully squeezed inx-direction.Also,it is seen that,larger values ofσ0,result in sooner arriving of quadrature squeezing parameter to maximum value(?1).Our numerical calculations also show that the squeezing inp-direction does not occur at all.That is why the related results are not represented here.

3.2 Quasi-Probability Distribution Functions

Quasi-probability distribution functions are very useful tools for the description of the nonclassical states.In this subsection,we examine the Husimi and Wigner distribution functions.

(i)Husimi Distribution Function

The Husimi distribution function is defined as wherestands as the density operator corresponding to an arbitrary state.TheQ(α,α?)function is always positive,and the non-circularity of the cross section of this function represents the nonclassicality of the considered state.[33]The distribution functionQ(α,α?)for|ξ〉even,|ξ〉oddand|ξ〉sis respectively shown in the first,second and third rows of Fig.5.Two different times are taken into account.The first column is attributed tot=0.2 and the second one involvest=2.It is clearly seen that for the case oft=0.2,the compression along the Re(α)and Im(α)directions happens just for the case of the superposition of squeezed states(i.e.,Fig.5(e)).But,considering bigger times(t=2),the compression happens for all three states.

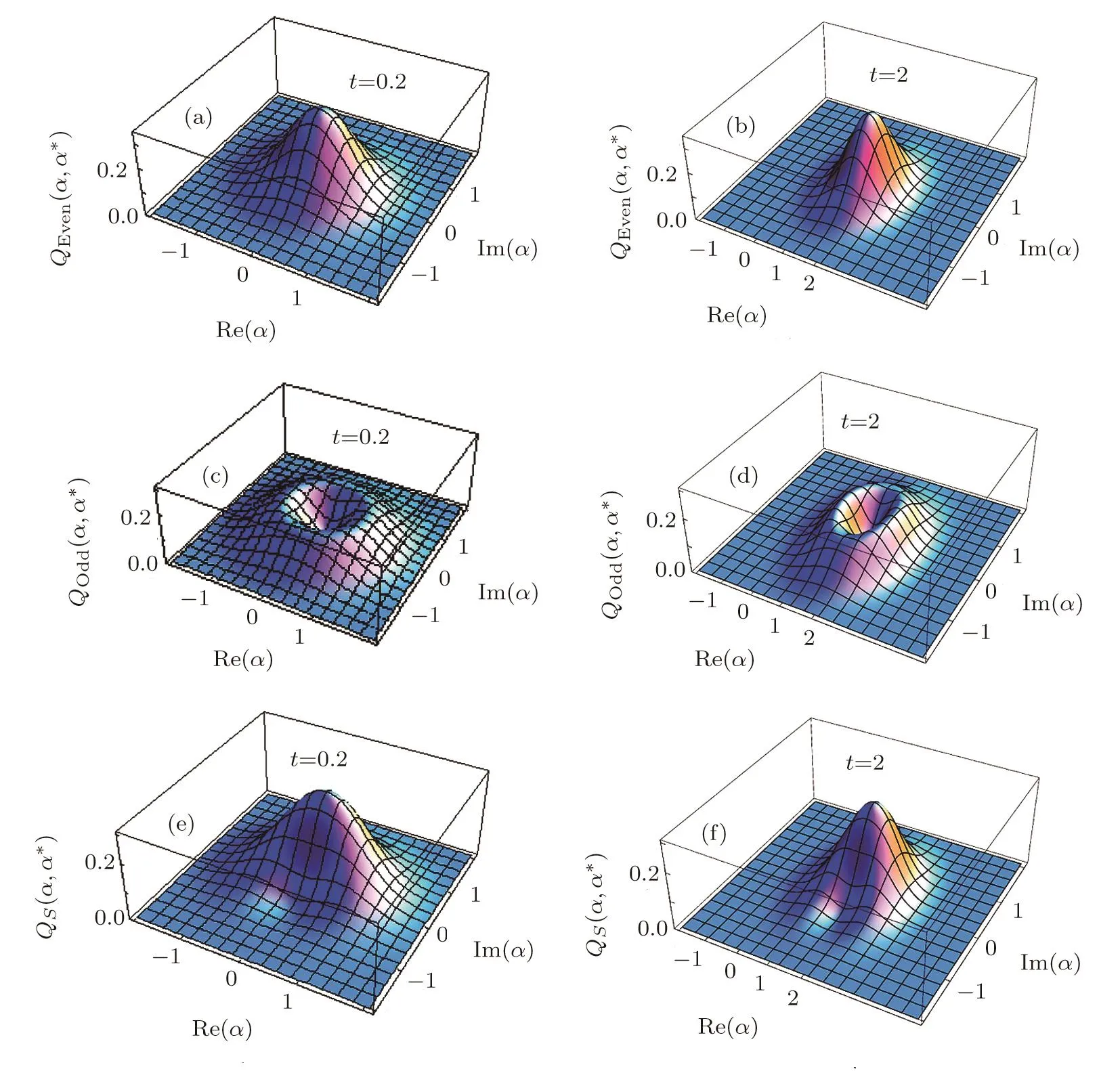
Fig.5 (Color online)Husimi distribution function for|ξ〉evenin Eq.(16)( first row),|ξ〉oddin Eq.(18)(second row)and|ξ〉sin Eq.(20)(third row)considering different scaled times with σ0=0.1.

(ii)Wigner Quasi-Distribution Function

This function is also a useful measure for the study of the nonclassical features of quantum states.This function for a quantum state with density operatorin the coherent states representation is defined as[1]

In fact,the negativity of Wigner function indicates the nonclassicality of a particular state.Upon the above equation,a more suitable form to calculate the Wigner function is derived in series form as[34]

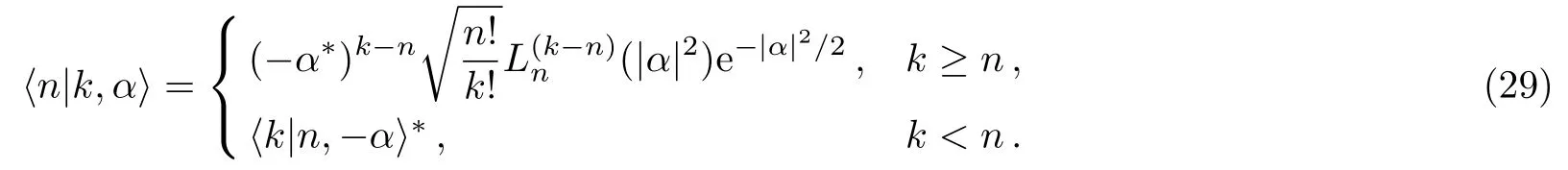
In Fig.6,considering constant value forσ0,the variation of Wigner function for the three types of squeezed states considering two different times is depicted.Regarding the chosen instants of time,it is seen that the Wigner function for the TCDE squeezed states is completely positive,but for other two squeezed states(i.e.,TCDO and their superposition)possesses negative values,which declare the nonclassicality of the discussed states.

Fig.6 (Color online)Wigner quasi-distribution function for|ξ〉evenin Eq.(16)( first row),|ξ〉oddin Eq.(18)(second row)and|ξ〉sin Eq.(20)(third row)considering different scaled times with σ0=0.9.

4 Time-and Conductivity-Dependent Excited Even and Odd(TCDEE/O)Coherent States

In this section we employ two even(|α〉+)and odd(|α〉?)coherent states,which are defined as the eigenstates of double-annihilation operator i.e.,The explicit form of the mentioned states are as

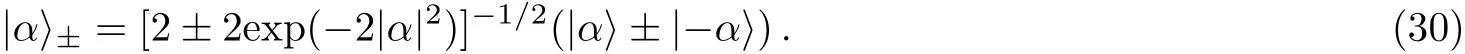
Now,we define two new time-and conductivity-dependent excited even/odd(TCDEE/O)coherent states,which are produced bym?times action of the operator?(in Eq.(11))on the even and odd coherent states as

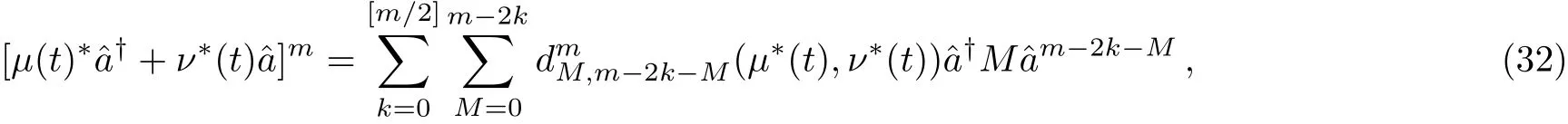
where

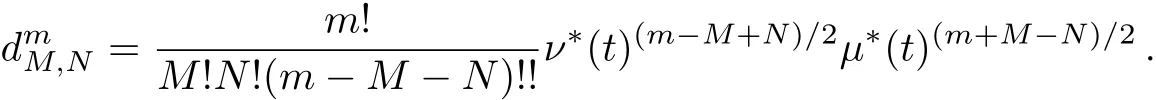
In order to study the properties of the TCDEE/O coherent states,we need to obtain the matrix elements based on the coherent state representations of Eq.(31).The general form of these matrix elements can be defined aswhich can be calculated as

where we have defined

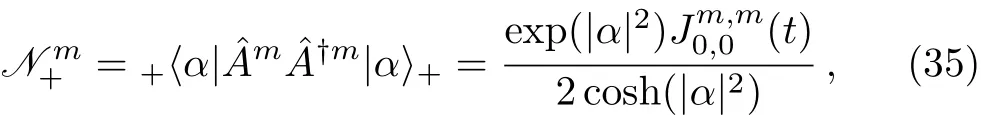
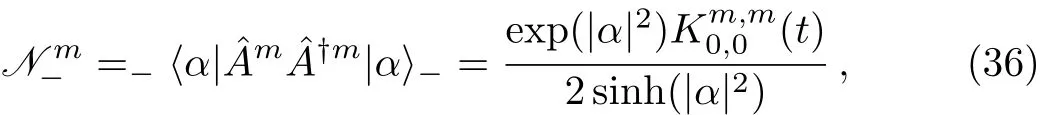
where we have defined

Now,we are ready to investigate the time-behavior of the nonclassical properties of the introduced states in Eq.(31),which is the task of the following subsections.

4.1 Sub-Poissonian Statistics

Using Eq.(25)the exact form of Mandel parameter for the TCDEE coherent states in Eq.(31)is obtained as

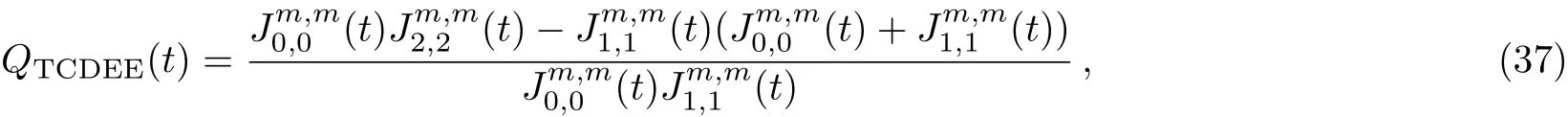
and for the TCDEO coherent states is

In Fig.7(a)the dynamics of this parameter for time-and conductivity-dependent excited even and odd coherent sates in Eq.(31)are displayed.Our numerical calculations show that the curves corresponding to TCDEE/O coherent states have a very small difference with each other,which can not be displayed in the graphs.For this reason,we present the results related to TCDEE/O coherent states in one curve for each value of excitation numberm,in Fig.7(a).As can be seen,all plots lie in negative territory in all times,indicating nonclassicality of the considered states independent of time.Also,it was observed that at a given time with an increased excitationm,the nonclassicality of the introduced states is increased.In addition,for a given amount of excitationm,this nonclassicality is reduced over time and in all cases it tends to a constant(and negative)value.The effect of conductivity parameter on the behavior of MandelQ-parameter versus|α|2for TCDEE/O coherent states of Eq.(31)is investigated in Fig.7(b).It is demonstrated that the whole of the curves lie in the negative region,which declares the nonclassicality of the obtained states.As is observed,by slightly increase in the value of intensity|α|2,the curves have a gradual tendency to zero.Also,it is seen that by increasing the value ofσ0,the negativity(and consequently the degree of nonclassicality)is decreased for given values of|α|2.

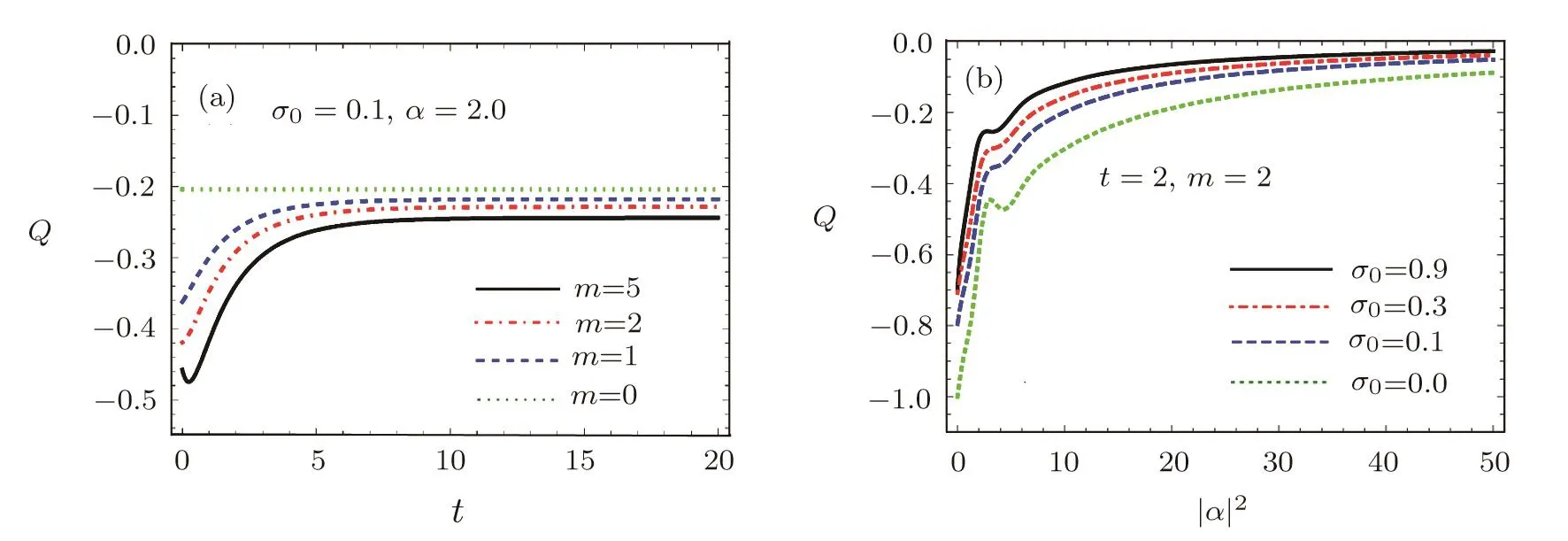
Fig.7 (Color online)The behavior of Mandel parameter for TCDEE/O coherent states in Eq.(31)(a)Versus scaled time t,(b)Versus|α|2.

4.2 Wigner Quasi-Distribution Function

The exact form of the Wigner functions for the TCDEE/O coherent states in Eq.(31)are obtained by using Eq.(27)as:

respectively.

Three-dimensional diagrams in Figs.8 and 9 respectively display the Wigner function for TCDEE/O coherent states in two different times.As is clear from these graphs,the negativity of Wigner function at different times is observed,which declares that the nonclassicality of the discussed states is visible in these times.Also,in Fig.10,the Wigner function for TCDEE/O coherent states considering three different values ofσ0is displayed and by these means the in fluence of conductivity parameter on this function is observed.

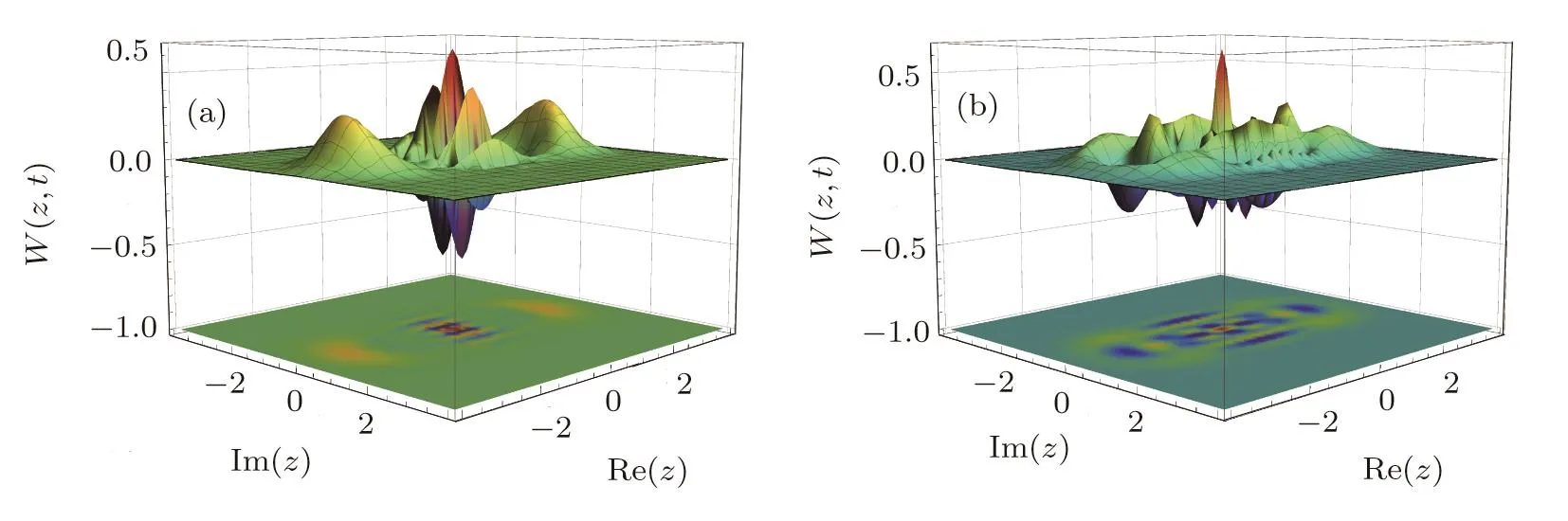
Fig.8 (Color online)Wigner quasi-distribution function for TCDEE coherent states in Eq.(31)with m=2,σ0=0.1,and α =2i,with different scaled times(a)t=2 and(b)t=10.

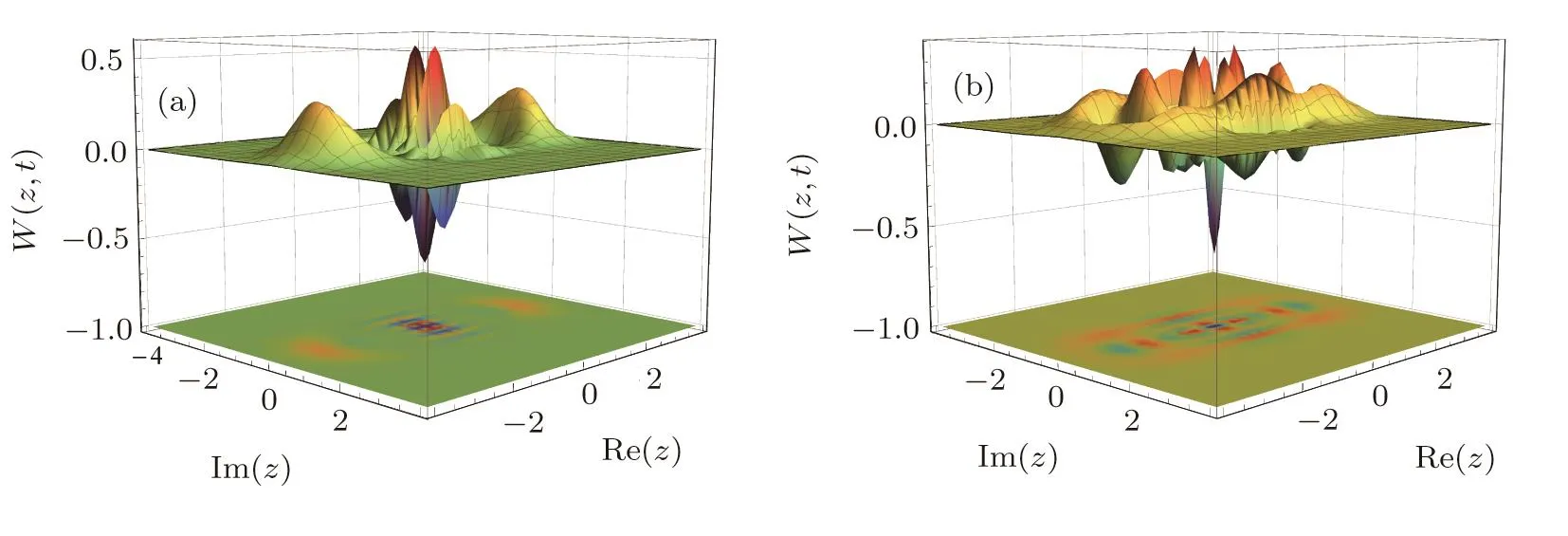
Fig.9 (Color online)Wigner quasi-distribution function for TCDEO coherent states in Eq.(31)with m=2,σ0=0.1,and α =2i,with different scaled times(a)t=2 and(b)t=10.

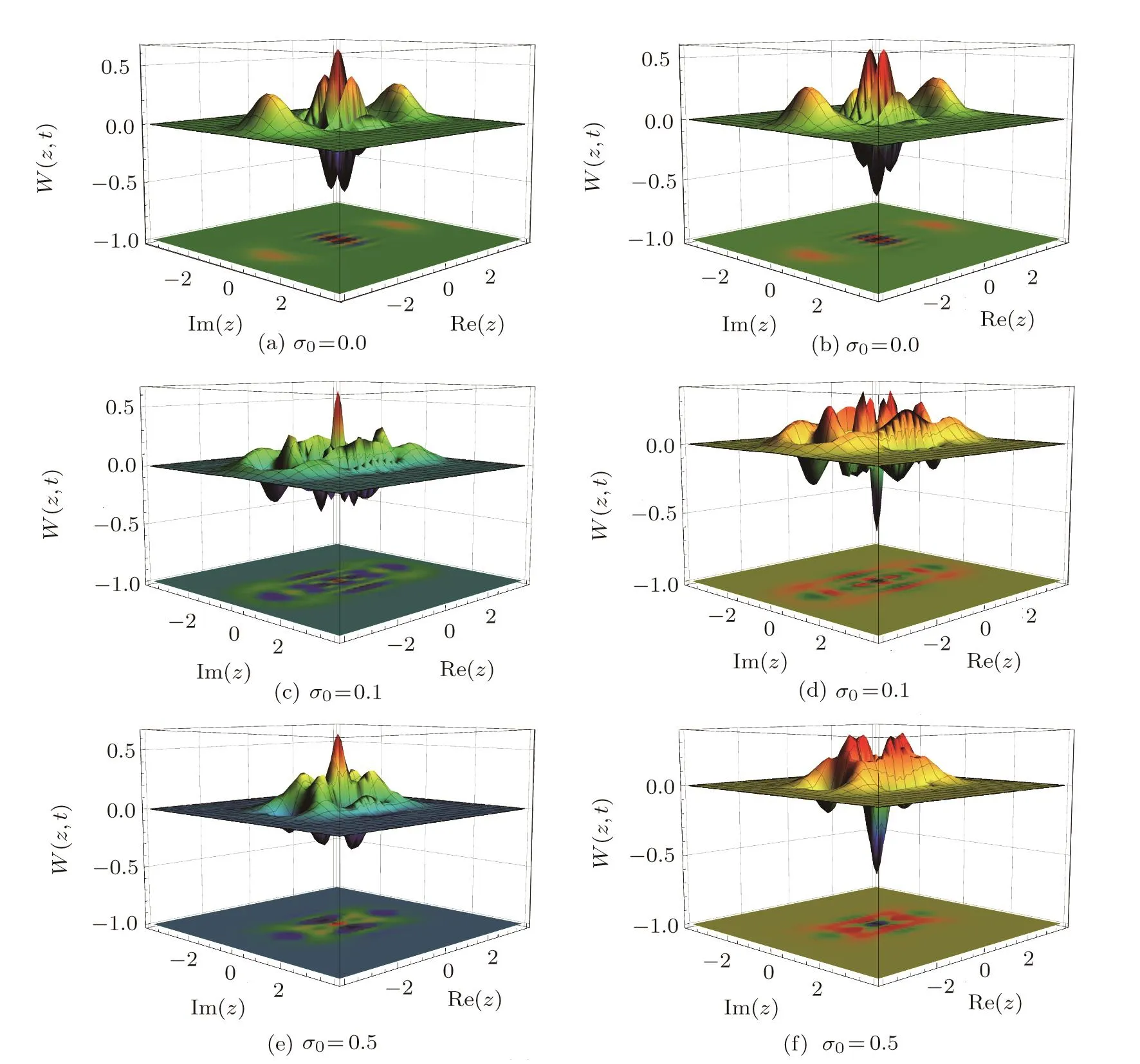
Fig.10 (Color online)Wigner quasi-distribution function for TCDEE(left)and TCDEO(right)coherent states in Eq.(31)with m=2,t=10 and α=2i.

5 Summary and Conclusion

Introducing nonclassical states,in particular,associated with real physical systems are still among the most useful subjects in quantum optics,due to their applications in quantum information processing.[35?37]In this paper,after producing a few new classes of timeand conductivity-dependent squeezed sates and excited even/odd coherent states related to the electromagnetic field propagating in conducting media,their nonclassicality behavior have been studied.In the path of the goal of paper,we started with a brief review on the quantization of electromagnetic waves in a conductive medium,where it is established that when the coeきcients of conductivity and permittivity of the environment are non-zero,dynamics of the amplitude of electromagnetic field undergoes dissipation.In particular,when these characteristic parameters of radiation field are constant,the corresponding Hamiltonian of the field is well-described by the CK Hamiltonian.Whereas the Hamiltonian of the corresponding field is time-dependent,obtaining the eigenstates and investigating other quantum properties are not so straightforward.In this situation,the time-invariant operator method has been employed.As the outcome of this method,the generalized annihilation and creation operators of the field can be written in terms of the standard annihilation and creation operators of the simple harmonic oscillator,which are expressed by Bogoliubov transformations with time-dependent coeきcients.In this way,it has been concluded that the eigenstates of the annihilation operator are squeezed states with eigenvalue zero.Therefore,the exact form of the eigenstates of the squeezing operator of the corresponding field have been obtained.These eigenstates have been called by us as TCDE and TCDO squeezed states.In the continuation,we have taken into account the superposition of the latter states.After that,the nonclassical properties of the introduced states such as sub-Poissonian statistics,quadrature squeezing of the field and some quasi-distribution functions i.e.,Husimi and Wigner functions have been studied.

It has been observed that,upon the chosen values for the conductivity parameter,the value of MandelQ-parameter for TCDE squeezed states is always positive.While,for other two states(i.e.,TCDO and superposition of the squeezed states),it has been seen that for the early times,the sub-Poissonian statistics can be observed.However,by passing the time,the MandelQ-parameter enters the positive region.Also,it has been shown that the introduced states are squeezed inx-direction specially for the TCDE squeezed states at all times.For the other two obtained states,the plot of squeezing parameter starts from positive region and after passing some time,the states will be squeezed.In the continuation,the behavior of Husimi and Wigner quasi-distribution functions for different times have been displayed.It has been observed that the superposition of states shows compression(as a sign of nonclassicality of the desired states)in both directions,but for other two states the compression is not seen for the small values of time.Also,for the Wigner function it has been seen that regarding the chosen instants of time,this function for the TCDE squeezed states is completely positive,but for the other two produced states(i.e.,TCDO squeezed states and superposition of squeezed states)the negative values have been observed,indicating the nonclassicality of the states.

As the final aim of this paper,the time-and conductivity-dependent excited even and odd(TCDE E/O)coherent states corresponding to the electromagnetic waves in conducting medium have been generated.Then,some nonclassical features of such states have been studied.In assessment of the time behavior of MendelQ-parameter,it has been observed that in all times,this parameter is in negative territory for both TCDEE/O coherent states and by increasing the excitation,the curve is shifted to more negative values(thus,by increasing the amount of excitation,the non-classical features appear much strongly).Also,the in fluence of conductivity parameter on the behavior of Mandel parameter has been investigated.It has been observed again that for different values of conductivity,the curve of Mandel parameter lies completely in the negative region and by increasing the value of conductivity,the negativity and the degree of nonclassicality of the discussed states is decreased.Our study also has found that the Wigner function possesses negative values at different times for the considered values of conductivity parameter,which again con firms the nonclassical nature of the TCDEE/O squeezed states.

We would like to announce that,very recently we have shown that the Caldirola–Kanai Hamiltonian approach provided us a useful framework also for the generation of new classes of multipartite entangled coherent squeezed states in a conducting cavity,too(see Ref.[38]).

Summing up,we have shown that the degree of nonclassicality of the introduced states can be adjusted by tuning the conductivity of media.

[1]M.O.Scully and M.S.Zubairy,Quantum Optics,Cambridge University Press,Cambridge(1997).

[2]J.R.Choi,Phys.Scr.70(2004)271.

[3]J.B.Xu,X.S.Zhang,and S.B.Li,Phys.Scr.56(1997)225.

[4]E.Kanai,Prog.Theor.Phys.3(1948)440.

[5]P.Caldirola,Il Nuovo Cimento 18(1941)393.

[6]P.Caldirola,II Nuovo Cimento B 77(1983)241.

[7]M.Razavy,Classical and Quantum Dissipative Systems,World Scientific,Imperial College Press,London(2005).

[8]U.Weiss,Quantum Dissipative Systems,World Scientific,London(1999).

[9]Jr.Lewis,H.Ralph,and W.B.Riesenfeld,J.Math.Phys.10(1969)1458.

[10]I.A.Pedrosa and A.Rosas,Phys.Rev.Lett.103(2009)010402.

[11]I.A.Pedrosa,Phys.Rev.A 83(2011)032108.

[12]H.P.Yuen,Phys.Rev.A 13(1976)2226.

[13]I.Pedrosa and A.Pinheiro,Prog.Theor.Phys.125(2011)1133.

[14]C.Gerry and P.Knight,Introductory Quantum Optics,Cambridge University Press,Cambridge(2005).

[15]A.NoormandiPour and M.K.Tavassoly,Commun.Theor.Phys.61(2014)521.

[16]E.Dibakar,A.Karimi,and M.Tavassoly,Phys.Scr.90(2015)085102.

[17]A.E.Bernardini and S.S.Mizrahi,Phys.Scr.90(2015)074011.

[18]V.V.Dodonov,V.I.Man’Ko,and D.E.Nikonov,Phys.Rev.A 51(1995)3328.

[19]C.C.Gerry and E.E.Hach,Phys.Lett.A 174(1993)185.

[20]S.A.M.Vamegh and M.K.Tavassoly,Rep.Math.Phys.75(2015)149.

[21]E.Piroozi and M.K.Tavassoly,J.Phys.A:Math.Theor.45(2012)135301.

[22]G.R.Honarasa,M.K.Tavassoly,M.Hatami,and R.Roknizadeh,J.Phys.A:Math.Theor.44(2011)085303.

[23]M.Zarezadeh and M.K.Tavassoly,Rep.Math.Phys.72(2013)153.

[24]Y.Xia and G.Guo,Phys.Lett.A 136(1989)281.

[25]O.Abbasi and M.K.Tavassoly,Opt.Commun.282(2009)3737.

[26]S.Mancini,Phys.Lett.A 233(1997)291.

[27]A.Mohammadbeigi and M.K.Tavassoly,Pramana 86(2016)763.

[28]R.N.Daneshmand and M.K.Tavassoly,Laser Phys.25(2015)055203.

[29]W.Wu and L.A.Wu,J.Opt.B:Quantum Semiclass.Opt.5(2003)364.

[30]S.P.Kim,J.Phys.A:Math.Theor.36(2003)12089.

[31]A.Vourdas and R.M.Weiner,Phys.Rev.A:Math.Theor.36(1987)5866.

[32]J.r.Choi,Int.J.Mod.Phys.B 18(2004)2307.

[33]M.J.Collett,Phys.Rev.Lett.70(1993)3400.

[34]V.Buˇzzek,G.Adam,and G.Drobn′y,Ann.Phys.245(1996)37.

[35]B.Vlastakis,G.Kirchmair,Z.Leghtas,S.E.Nigg,L.Frunzio,S.M.Girvin,M.Mirrahimi,M.H.Devoret,and R.J.Schoelkopf,Science 342(2013)607.

[36]M.D.Lang and C.M.Caves,Phys.Rev.Lett.105(2010)150501.

[37]S.Y.Lee and H.Nha,Phys.Rev.A 82(2010)053812.

[38]R.Daneshmand and M.K.Tavassoly,Ann.Phys.1600 246(2017)/DOI10.1002/andp.201600246.