Deterministic Remote State Preparation via the χ State?
Pei Zhang(張佩),Xian Li(李嫻),Song-Ya Ma(馬松雅),,3,? and Zhi-Guo Qu(瞿治國(guó))3School of Mathematics and Statistics,Henan University,Kaifeng 475004,China
2School of Mathematics and Statistics,North China University of Water Resources and Electric Power,Zhengzhou 450046,China
3Jiangsu Engineering Center of Network Monitoring,Nanjing University of Information Science&Technology,Nanjing 210044,China
1 Introduction
Information security is regarded as one of the most essential issues for network technology,especially when cloud computing technology is widely spreading.[1?6]In order to resolve this issue,quantum networks are rapidly developing as the next generation networks,in which the secure transmission of a quantum state has drawn much attention as quantum state is the carrier of the information.However,the state should not be directly sent because any enemy can easily replace it by a fake one without recognition of the authorized parties. Taking the place of sending the state itself physically,Bennett et al.[7]first proposed a celebrated protocol called quantum teleportation(QT).QT allows for the transmission of an unknown state to a distant location with the help of previously shared entanglement and classical communication.Whereafter,another quantum transmission protocol called remote state preparation(RSP)was presented.[8]In RSP,the transmitted state is a pure known state.On account of the sender’s prior knowledge about the original state,RSP protocols are more economical than QT for some special ensembles of states.For instance,it requires only one cbit from the sender to the receiver for a qubit chosen from equatorial circles on a Bloch sphere,[9]while two cbits are consumed in standard QT.Bennett et al.[10]studied the trade-offbetween the classical communication cost(CCC)and the required entanglement in RSP.In addition to the traditional RSP with two parties,multi-party RSP[11?23]plays an important role in the general quantum network communication and quantum distributed computation.One branch of multi-party RSP is called joint remote state preparation(JRSP).[11?17]Different from RSP that all the secret information is provided by one sender,which may lead to the leakage of information,JRSP deals with the situation that the complete classical knowledge of the state is independently shared among numbers of senders who have to cooperatively complete the task.The other is named as controlled remote state preparation(CRSP),[18?23]which transmits a state in a controlled manner.In CRSP,one or several controllers are introduced in addition to the sender and the receiver.Although the controlling party has no information about the prepared state,he determines whether the state is constructed for the receiver or not.So far,generalizations were made for RSP such as oblivious RSP,low-entanglement RSP,optimal RSP,faithful RSP,deterministic RSP,etc.[11?36]In the meanwhile,experimental implementation of RSP has been demonstrated.[37?42]
Various entangled resources such as EPR pair,GHZ state,W sate,cluster state or Brown state have been exploited for carrying out RSP since the appearance of RSP.Why different entangled states are explored as the quantum channel to realize RSP?This is because various entanglement may be used in some peculiar circumstances due to the security consideration and their own features.Particularly,in some special case only some kinds of entangled states are available,one has to use them to try to fulfill tasks instead of doing nothing.In this sense,it is interesting and useful to explore the ability of various entangled states for implementing RSP tasks.Yeo et al.[43]researched a maximally entangled four-qubitχ-state,which distinguishes from a four-qubit GHZ or W state un-der stochastic local operations and classical communication.Also,it has many interesting properties and is a very significant entangled resource.For example,χ-state has been widely applied in QT,superdense coding,[43]quantum secure direct communication,[44]quantum information splitting.[45]and quantum steganography.[46]Recently,Ma et al.[35]investigated its application in RSP for arbitrary two-and three-qubit states.The success probabilities are 50%when the coeffcients are complex.Success probability is one of the most important indexes to evaluate a protocol.Thus,deterministic RSP(or CRSP,JRSP)has attracted much attention and been intensively studied in recent years.[13?15,17,23,32]Of course,it would be better to consume less resource if achieving unit success probability.In 2012,Zhan et al.[32]put forward two deterministic schemes for remote preparation of arbitrary twoand three-qubit states with complex coeffcients via the GHZ state as the quantum channel.To our knowledge,there are no deterministic RSP(or CRSP,JRSP)schemes via theχstate till now.
In this paper,we are concerned with the question“can one make a general RSP of arbitrary two-and three-qubit states via theχstate with unit success probability?” and propose two deterministic schemes.In Sec.2,the RSP for an arbitrary two-qubit state is elucidated in detail.New sets of measurement bases are constructed,which play a key role in our scheme.It is shown that the state can be prepared with unit success probability if the sender performs two-step projective measurement under these bases and the receiver adopts some appropriate unitary transformations.In Sec.3,the other deterministic remote state preparation(DRSP)scheme with the aid of another new orthogonal bases is put forward for remote preparation of an arbitrary three-qubit state.Compared with the previous protocols,[35]the success probabilities of the two schemes are both greatly improved.Some discussions and conclusions are drawn in the last Section.
2 Deterministic RSP for an Arbitrary Two-Qubit State
In this section,the remote preparation of an arbitrary two-qubit state utilizingχstate as the entangled resource is put forward.The sender Alice wants to help the receiver Bob remotely prepare an arbitrary two-qubit state

wheresj,j=0,...,3 are arbitrary complex numbers and satisfyAlice is aware of the informations0,s1,s2,s3,while Bob does not know them at all.
Assume that two participants share theχstate
as the quantum channel,where

Besides theχstate,Alice introduces two EPR pairsAlice and Bob hold the qubits(1,2,5,7,6,8)and(3,4),respectively.

The detailed steps are shown as follows.
Step 1The scheme takes the aim at realizing the RSP with unit success probability.Thus,the sender Alice needs to construct sets of useful measurement bases that relies on the coeffcientss0,...,s3of the prepared state.Denote It is noticed thatSince Alice knowssj,she knowstjcompletely.Splittj=rjeiθjinto the amplitude informationrjand phase informationθj,j=0,...,3.
Alice performs a four-qubit projective measurement on her qubits(1,2,5,7)under the orthogonal basis|ξ0〉,...,|ξ15〉,which has the following relationship to the computation basis|0000〉,...,|1111〉
where


After the measurement,the entangled channel in Eq.(4)can be expressed in terms of the basis|ξ0〉,...,|ξ15〉as
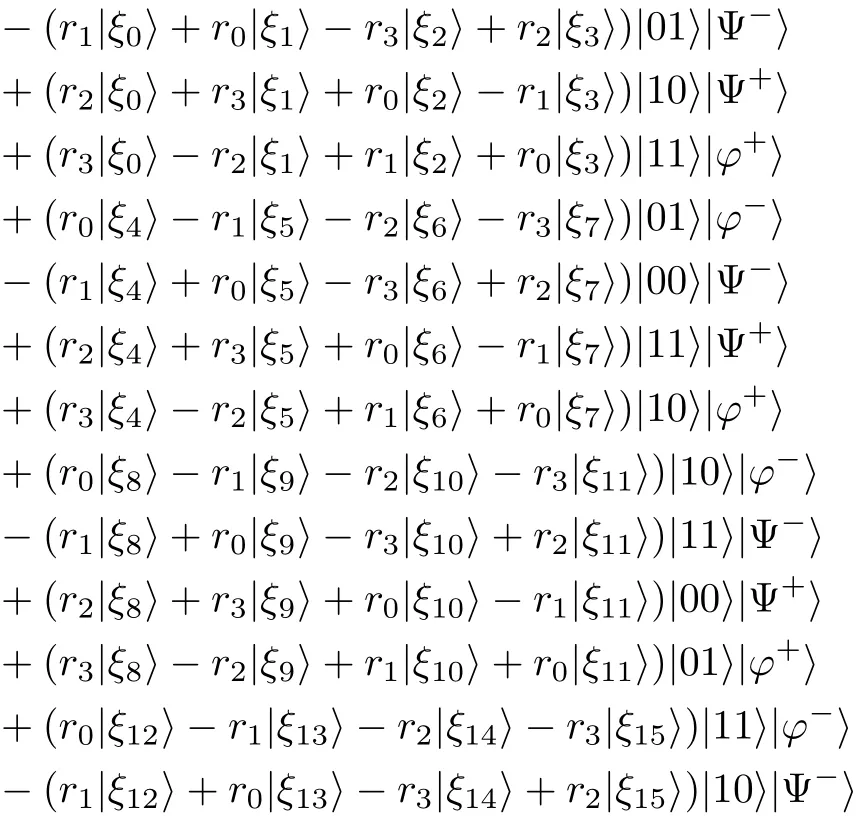
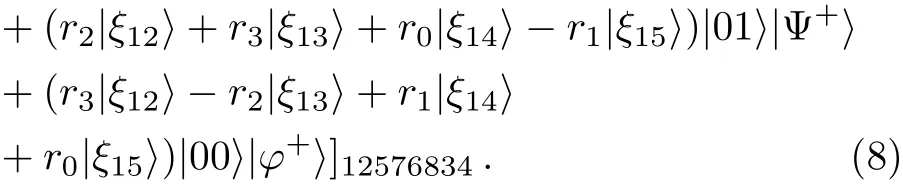
Step 2After the first-step measurement,Alice performs a unitary operationUn1on her particles(6,8)before performing the second-step measurement.The unitary operation is conditioned on her first-step measurement result|ξn1〉,n1∈ {0,...,15}.Here

Then Alice performs a two-qubit projective measurement on her qubits(6,8)under the following orthogonal basis
After the two-step projective measurements,Alice transmits the classical messagen1n2to Bob if her measurement outcome is|ξn1〉|ηn2〉,n1=0,...,15,n2=0,...,3.
Step 3In order to recover the prepared state,Bob needs to perform local unitary operation according to the classical message from Alice.
Here,we show part of the process to see how the protocol works.Without loss of generality,assume Alice’s first-step measurement result is|ξ4〉1257.As a result,the particles(6,8,3,4)collapse into
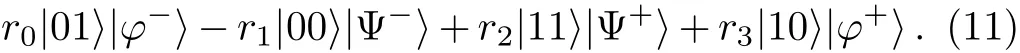
In this situation,Alice performs the unitary operationU4=I6X8on her particles(6,8)and gets
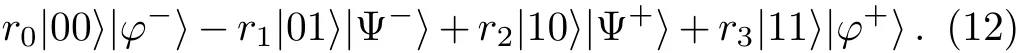
Then Alice performs a two-qubit projective measurement on her qubits(6,8)under the basis|η0〉,...,|η3〉defined by Eq.(10).The state in Eq.(12)can be rewritten as

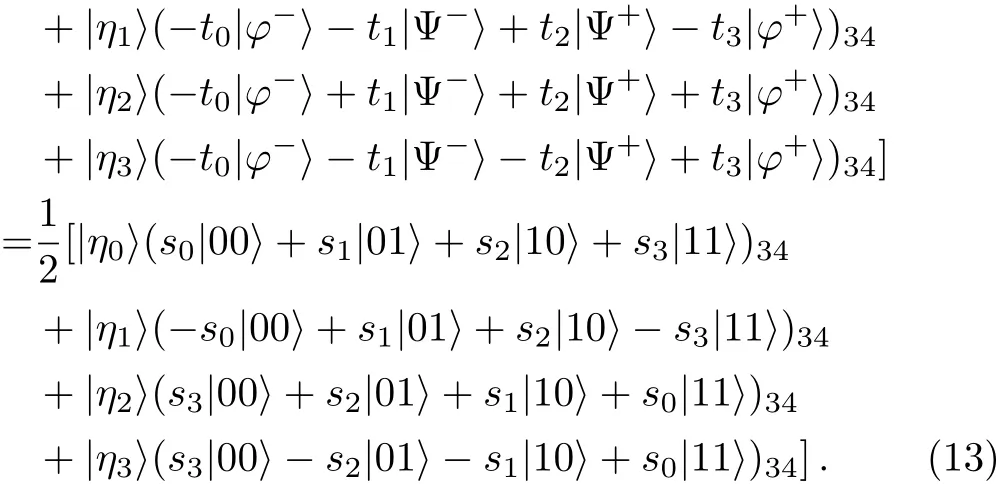
According to the above equation,one can see that Bob can always restore the original state at his side by means of proper unitary operations on his particles whatever Alice’s second measurement outcome is.
The other fifteen cases corresponding to Alice’s firststep measurement results can be analyzed similarly.The detailed recovery operations conditioned on Alice’s twostep measurement results are summarized in Table 1.So,the two-qubit state can be prepared with unit success probability.
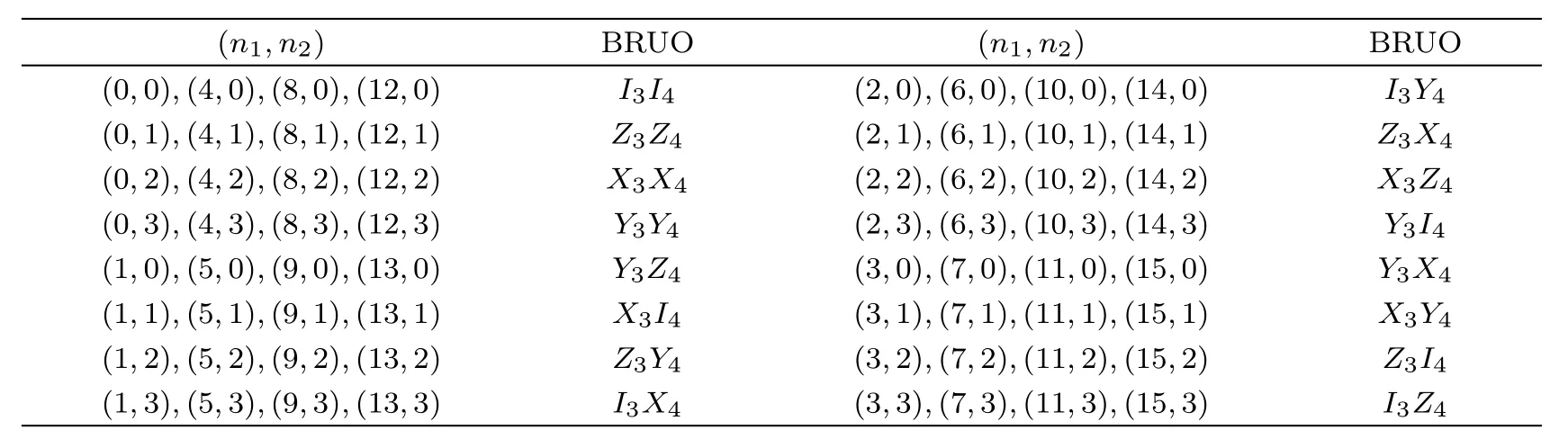
Table 1 The relation between Alice’s two-step measurement outcome|ξn1〉|ηn2〉(n1=0,...,15,n2=0,...,3)and Bob’s recovery unitary operation(BRUO)on the collapsed state,where I,X,Y,Z are the Pauli operations.
3 Deterministic RSP for an Arbitrary Three-Qubit State
In this section,we proceed to use theχstate to deterministically prepare an arbitrary three-qubit state
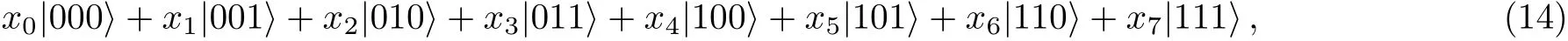
wherexj,j=0,...,7 are complex numbers and satisfyThe coeffcientsx0,...,x7are completely known to Alice,while Bob does not know them at all.
Besides the|χ〉1234in Eq.(2),Alice and Bob share two Bell statesand a GHZ state|GHZ〉A(chǔ)90=as the quantum channel.The particles(1,2,5,7,A,6,8,0)belong to the sender Alice,and the particles(3,4,9)belong to the receiver Bob.The combined system can be rewritten as

Now,we describe the RSP scheme for an arbitrary three-qubit state as follows.
Step 1To help the remote receiver Bob prepare the desired state with a high success probability,Alice needs to construct useful measurement bases.Denote
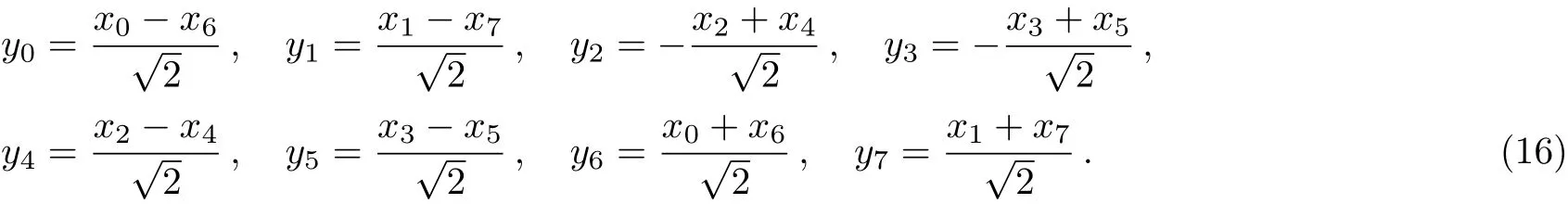

Alice performs a five-qubit projective measurement on her qubits(1,2,5,7,A)under the basis|ζ0〉,...,|ζ31〉,which is related to the computation basis|00000〉,...,|11111〉by the following relation

where

After the measurement,the entangled channel in Eq.(15)can be described in terms of the measurement basis|ζ0〉,...,|ζ31〉as

where
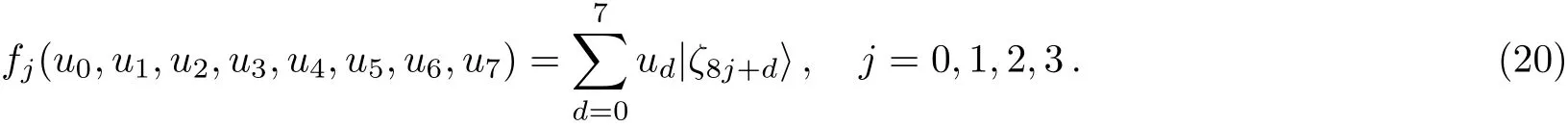
Step 2After the first-step measurement,Alice does not perform the second-step measurement immediately,but performs a unitary operationUm1on her particles(6,8,0)conditioned on her first-step measurement result|ζm1〉,m1=0,...,31.Here

Then Alice performs a three-qubit projective measurement on her qubits(6,8,0)under the complete orthogonal basis|τ0〉,...,|τ7〉,which is described by
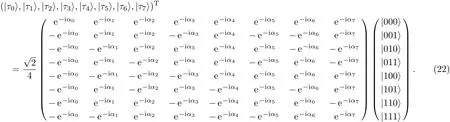
Alice tells the classical messagem1m2to Bob through the classical channel if her two-step measurement result is|ζm1〉|τm2〉,wherem1=0,...,31,m2=0,...,7.
Step 3The receiver Bob performs recovery unitary operations with the help of the received classical message to obtain the prepared state.
Suppose that Alice’s first-step measurement result is|ζ8〉1257A.As a result,the remaining system is
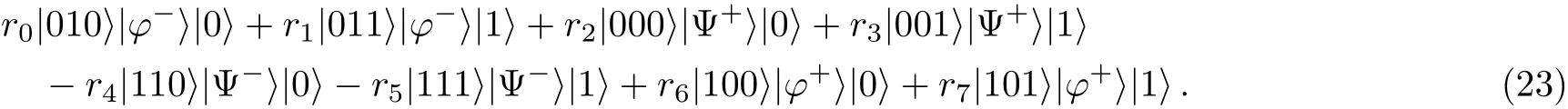
In this situation,Alice performs the unitary operationI6X8I0on her particles(6,8,0)and gets

The state in the above equation can be rewritten in terms of the measurement basis|τ0〉,...,|τ7〉as

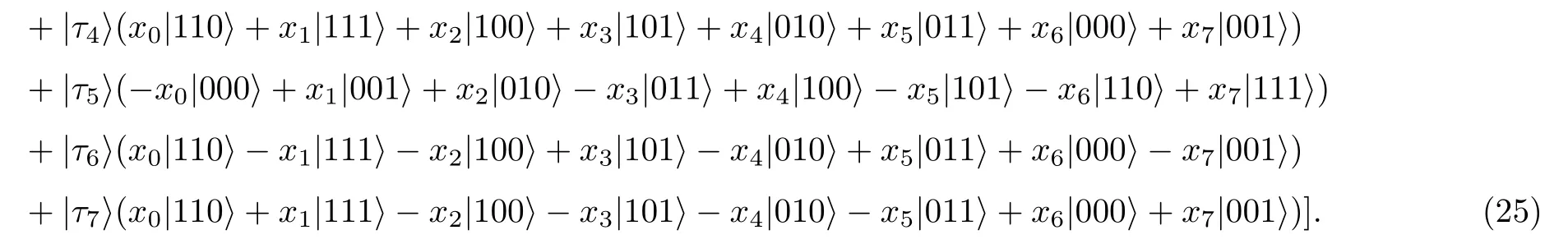
The above equation implies that Bob can always recover the prepared state by performing appropriate unitary operations on his collapsed particles when Alice’s first measurement result is|ζ8〉1257A.
As for the other 31 first-step measurement results,similar analysis can be made to show that Bob can always recover the prepared state by performing appropriate unitary operations on his collapsed particles whatever Alice’s second measurement result is.In summary,Bob’s recovery operations conditioned on Alice’s two-step measurement results are listed in Table 2.Therefore,the total success probability is unit.
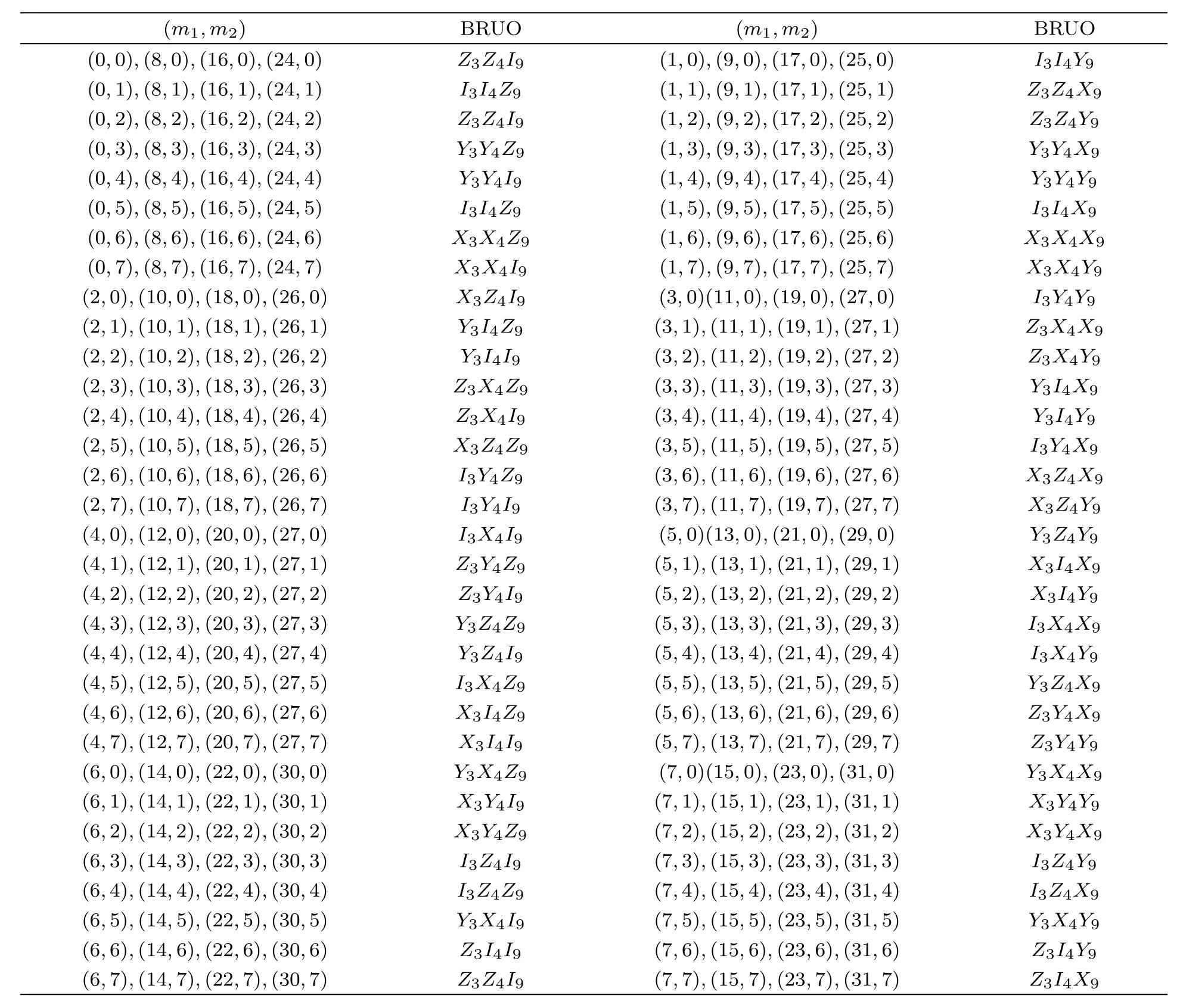
Table 2 The relation between the Alice’s two-step measurement outcome|ζm1〉|τm2〉(m1=0,...,31,m2=0,...,7)and Bob’s recovery unitary operation(BRUO)on the collapsed state.
4 Discussions and Conclusions
We have demonstrated two deterministic RSP schemes for arbitrary two-and three-qubit states via the four-qubit entangledχstate.It needs emphasizing that to accomplish the RSP tasks with high success probabilities,we construct a series of ingenious measurement bases at the sender’s location.In the first scheme,the sender first performs four-and two-qubit projective measurements under novel sets of measurement bases.And,before performing the second-step projective measurement,Alice needs to perform an additional unitary operation conditioned on her first-step measurement outcome.Then,the original state can be successfully prepared with the probability 100%.In the second scheme,we construct another novel sets of mutually orthogonal bases.Under these bases,the sender performs a two-step projective measurement on her qubits.After achieving the sender’s measurement results,the receiver can recover the prepared state deterministically.Compared with the previous DRSP protocols for arbitrary two-and three-qubit states via the GHZ state as the quantum channel,[32]the local unitary operations used in our schemes are only single-qubit Pauli operations without the use of Hadamard operations and other multiqubit unitary operations.Compared with previous RSP protocols via theχstate,[35]the success probabilities of our schemes are greatly improved while they still have no restriction on coeffcients of the prepared state.On the other hand,there are also some defects about our schemes.More particle projective measurements are required and more resource is consumed.It means that the sender’s workload is increased.In spite of this,our solutions are still interesting as the success probability is an important index to weigh a protocol.Moreover,the proposed schemes require local operations such as single-qubit Pauli transformations,two-,three-,four-and five-qubit projective measurements.It is known that single-qubit Pauli gate can be realized under the present technologies.By far,projective measurement has received a great deal of attention.[47?49]Some researchers have conjectured that any projective measurement can be decomposed into a sequence of weak measurements,[47?48]which cause only small changes to the state.Moreover,multi-particle projective measurement via linear optics,has been investigated by numerous spectacular works.[50?51]Thereby,our schemes are feasible in the framework of linear optics and may be demonstrated in prospective experiments.
It is worth mentioning that like many RSP and JRSP schemes,[12?17,31?32]the proposed schemes use the information splitting and divide the related complex coeff-cientsp+qi=reiθof the prepared state intorandθbefore constructing the measurement bases.Ifrandθare independently shared between two senders Alice1 and Alice2,the two senders cooperatively perform the corresponding measurements.Thus,the proposed schemes can be reduced to deterministic joint remote preparation schemes of arbitrary two-and three-qubit states via theχstate as the entangled channel.
[1]Z.J.Fu,X.M.Sun,Q.Liu,L.Zhou,and J.G.Shu,IEICE Trans.Commun.98(2015)190.
[2]Z.H.Xia,X.H.Wang,X.M.Sun,and Q.Wang,IEEE Trans.Parall.Distr.Syst.27(2016)340.
[3]Z.J.Fu,K.Ren,J.G.Shu,X.M.Sun,and F.X.Huang,IEEE Trans.Parall.Distr.Syst.27(2016)2546.
[4]Z.H.Xia,X.H.Wang,L.G.Zhang,Z.Qin,X.M.Sun,and K.Ren,IEEE Trans.Inform.Foren.Secur.11(2016)2594.
[5]Z.J.Fu,X.L.Wu,C.W.Guan,X.M.Sun,and K.Ren,IEEE Trans.Inform.Foren.Secur.11(2016)2706.
[6]Q.Liu,W.D.Cai,J.Shen,Z.J.Fu,X.D.Liu,and N.Linge,Secur.Commun.Netw.9(2016)4002.
[7]C.H.Bennett,G.Brassard,C.Crpeau,R.Jozsa,A.Peres,and W.K.Wootters,Phys.Rev.Lett.70(1993)1895.
[8]H.K.Lo,Phys.Rev.A 62(2000)012313.
[9]A.K.Pati,Phys.Rev.A 63(2001)014302.
[10]C.H.Bennett,D.P.DiVincenzo,P.W.Shor,J.A.Smolin,B.M.Terhal,and W.K.Wootters,Phys.Rev.Lett.87(2001)
[11]Y.Xia,J.Song,and H.S.Song,J.Phys.B:At.Mol.Opt.Phys.40(2007)3719.
[12]X.Q.Xiao,J.M.Liu,and G.H.Zeng,J.Phys.B:At.Mol.Opt.Phys.44(2011)075501.
[13]N.B.An,C.T.Bich,and N.V.Don,Phys.Lett.A 375(2011)3570.
[14]Q.Q.Chen,Y.Xia,and J.Song,J.Phys.A:Math.Theor.45(2012)055303.
[15]Y.Xia,Q.Q.Chen,and N.B.An,J.Phys.A:Math.Theor.45(2012)335306.
[16]P.Zhou,J.Phys.A:Math.Theor.45(2012)215305.
[17]Y.Wang and X.Ji,Chin.Phys.B 22(2013)
[18]Z.Y.Wang,Y.M.Liu,X.Q.Zuo,and Z.J.Zhang,Commun.Theor.Phys.52(2009)235.
[19]X.B.Chen,S.Y.Ma,Y.Su,R.Zhang,and Y.X.Yang,Quant.Inform.Process.11(2012)1653.
[20]C.Gao,S.Y.Ma,and W.L.Chen,Int.J.Theor.Phys.55(2016)2643.
[21]C.Wang,Z.Zeng,and X.H.Li,Quant.Inform.Process.14(2015)1077.
[22]W.Dong and Y.Liu,Quant.Inform.Process.12(2013)3223.
[23]D.Zhang,X.W.Zha,Y.J.Duan,and Y.Q.Yang,Quant.Inform.Process.15(2016)2169.
[24]I.Devetak and T.Berger,Phys.Rev.Lett.87(2001)197901.
[25]D.W.Leung and P.W.Shor,Phys.Rev.Lett.90(2003)127905.
[26]D.W.Berry and B.C.Sanders,Phys.Rev.Lett.90(2003)057901.
[27]M.Y.Ye,Y.S.Zhang,and G.C.Guo,Phys.Rev.A 69(2004)022310.
[28]Z.Kurucz,P.Adam,Z.Kis,and J.Janszky,Phys.Rev.A 72(2005)052315.
[29]H.Y.Dai,P.X.Chen,L.M.Liang,and C.Z.Li,Phys.Lett.A 355(2006)285.
[30]Y.H.Wang and H.S.Song,Opt.Commun.281(2008)489.
[31]J.M.Liu,X.L.Feng,and C.H.Oh,Eurphys.Lett.87(2009)30006.
[32]Y.B.Zhan,Eurphys.Lett.98(2012)40005.
[33]P.C.Ma and Y.B.Zhan,Opt.Commun.283(2010)2640.
[34]S.Y.Ma,X.B.Chen,M.X.Luo,R.Zhang,and Y.X.Yang,Opt.Commun.284(2011)4088.
[35]S.Y.Ma and M.X.Luo,Chin.Phys.B 23(2014)090308.
[36]J.F.Li,J.M.Liu,X.L.Feng,and C.H.Oh,Quant.Inform.Process.15(2016)2155.
[37]X.Peng,X.Zhu,X.Fang,M.Feng,M.Liu,and K.Gao,Phys.Lett.A 306(2003)271.
[38]N.A.Peters,J.T.Barreiro,M.E.Goggin,T.C.Wei,and P.G.Kwiat,Phys.Rev.Lett.94(2005)150502.
[39]W.Rosenfeld,S.Berner,J.Volz,M.Weber,and H.Weinfurter,Phys.Rev.Lett.98(2007)050504.
[40]J.T.Barreiro,T.C.Wei,and P.G.Kwiat,Phys.Rev.Lett.105(2010)030407.
[41]N.Killoran,D.N.Biggerstaff,R.Kaltenbaek,K.J.Resch,and N.Lutkenhaus,Phys.Rev.A 81(2010)012334.
[42]M.Erhard,H.Qassim,H.Mand,E.Karimi,and R.W.Boyd,Phys.Rev.A 92(2015)022321.
[43]Y.Yeo and W.K.Chua,Phys.Rev.Lett.96(2006)060502.
[44]S.Lin,Q.Y.Wen,F.Gao,and F.C.Zhu,Phys.Rev.A 78(2008)064304.
[45]X.W.Wang,L.X.Xia,Z.Y.Wang,and D.Y.Zhang,Opt.Commun.283(2010)1196.
[46]Z.G.Qu,X.B.Chen,M.X.Luo,X.X.Niu,and Y.X.Yang,Opt.Commun.284(2011)2075.
[47]Y.Aharonov,D.Z.Albert,and L.Vaidman,Phys.Rev.Lett.60(1988)1351.
[48]Y.Aharonov and L.Vaidman,Phys.Rev.A 41(1990)11.
[49]L.M.Johansen,Phys.Rev.A 76(2007)012119.
[50]P.V.Loock and N.Lütkenhaus,Phys.Rev.A 69(2004)012302.
[51]M.Takeoka,M.Sasaki,P.V.Loock,and N.Lütkenhaus,Phys.Rev.A 71(2005)022318.
 Communications in Theoretical Physics2017年5期
Communications in Theoretical Physics2017年5期
- Communications in Theoretical Physics的其它文章
- Elastic Deformation Analysis on MHD Viscous Dissipative Flow of Viscoelastic Fluid:An Exact Approach
- Magnetic Effect Versus Thermal Effect on Quark Matter with a Running Coupling at Finite Densities?
- Borromean Windows for Three-Particle Systems under Screened Coulomb Interactions?
- Isotopic Effects on Stereodynamics of the C++H2→ CH++H Reaction?
- Entropy Generation Analysis in Convective Ferromagnetic Nano Blood Flow Through a Composite Stenosed Arteries with Permeable Wall
- Effects of Interfaces on Dynamics in Micro-Fluidic Devices:Slip-Boundaries’Impact on Rotation Characteristics of Polar Liquid Film Motors?
