Anumerical techniquebasedon collocation methodfor solvingmodi fi ed Kawaharaequation
Turgut Ak S. Bttl Gzi Krkoc
a Department of Transportation Engineering, Yalova University, Yalova, 77200 Turkey
b Department of Mathematics, Faculty of Science and Art, Nevsehir Haci Bektas Veli University, Nevsehir, 50300 Turkey
1.Introduction
The dynamics of shallow water waves is a seriously growing research area in the area of fl uid dynamics. There are several models that are available to focus on this area of research.A few well known models that are frequently visible in journals and text books are Korteweg–de Vries (KdV) equation[1–3] , modi fi ed KdV equation [4–8] , Peregrine equation [9] ,Benjamin–Bona–Mahony equation [10–12] , Boussinesq equation [13,14] and many more [15,16] . For coupled system,where two-layered shallow water waves are studied, several models are proposed there too. These are Bona–Chen equation [17] , Gear–Grimshaw model [18,19] , Zahreamoghaddam model [20] and others. This paper will focus on single layered shallow water fl uids that are observed along sea shores and beaches. The model that will be focused in this paper is known as modi fi ed Kawahara equation (mKE).
Modi fi ed Kawahara equation has been studied in the past during several occasions [21–28] . This equation models water waves in long wave regime for moderate values of surface tension [22] . It was analyzed that KdV equation fails in this context since the cubic term in dispersion relation vanishes and thus fi fth order dispersion terms stands relevant. The detail of this analysis is reported during 2006 [22] .
This paper discusses the numerical analysis of modi fi ed Kawahara equation using septic B-splines. The motion of single solitary waves is analyzed in details using this form of numerical simulations. Interaction of two and three solitary waves, stability analysis are all detailed in this paper with initial wave form being Gaussian type.
2.The governing equation and septic B-splines
In this study, we will consider the modi fi ed Kawahara equation
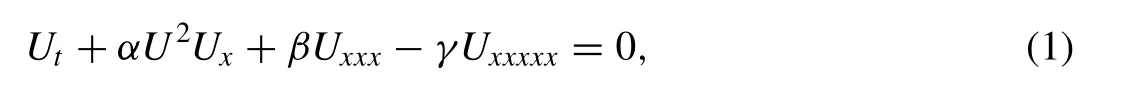
with the physical boundary conditionsU→ 0 asx→ ± ∞ ,whereα,βandγare positive parameters and the subscriptsxandtdenote the differentiation. To implement the numerical method, solution domain is restricted over an intervala≤x≤b. Boundary conditions will be selected from thefollowing homogeneous boundary conditions:

Table 1Septic B-spline function and its derivatives at nodes x m .
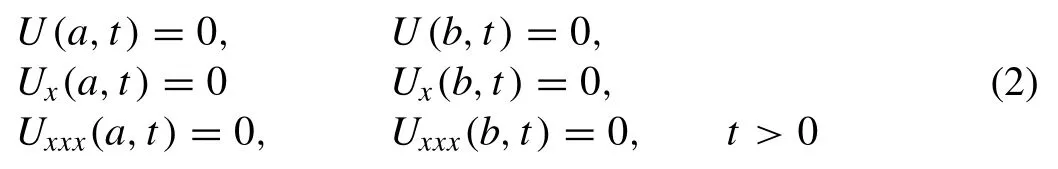
and the initial condition
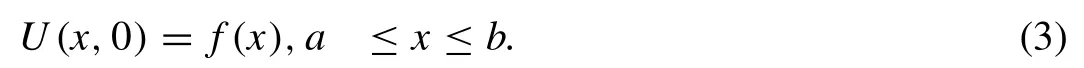
The septic B-splinesφm(x), (m= -3(1)N+ 3 ), at the knotsxmare de fi ned over the interval [a,b] by Ref. [29] .φm(x)
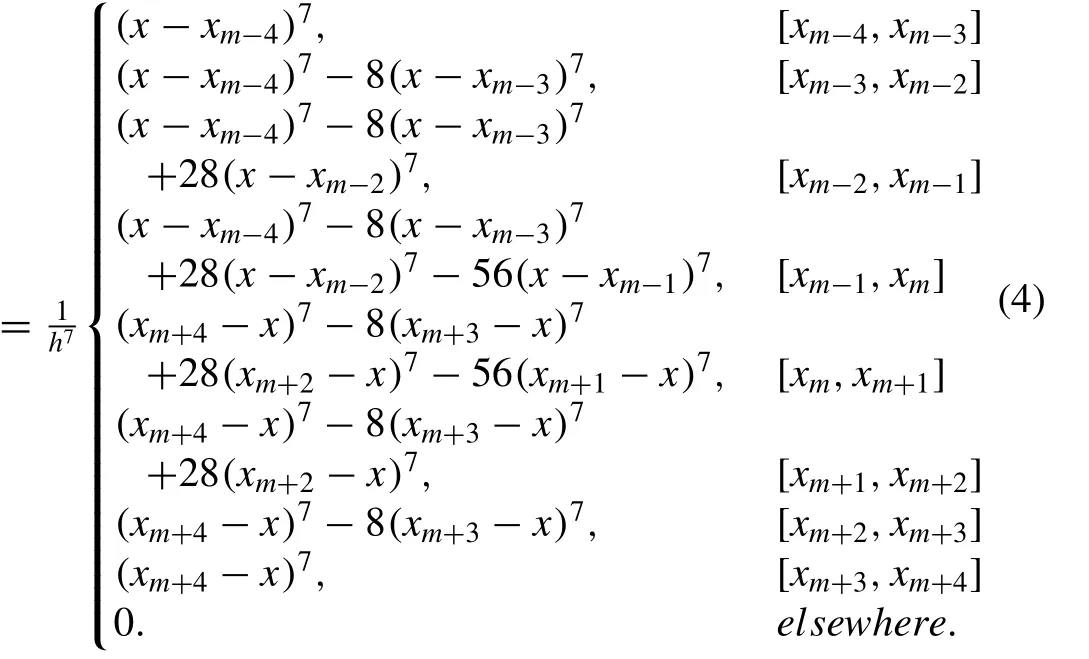
The set of functions {φ-3(x),φ-2(x),φ-1(x),...,φN+1(x),φN+2(x),φN+3(x)} forms a basis for functions de fi ned over[a,b]. The approximate solutionUN(x,t) to the exact solutionU(x,t) is given by

whereδi(t) are time dependent parameters to be determined from the boundary and weighted residual conditions. Each septic B-spline covers eight elements so that each element[xm,xm+1] is covered by eight splines. The values ofφm(x)and its derivative may be tabulated as in Table 1 .
Using trial function (5) and septic splines (4) , the values ofU,U′ ,U′ ′ ,U′′′ ,Uiv,Uv,Uviat the knots are determined in terms of the element parametersδmby
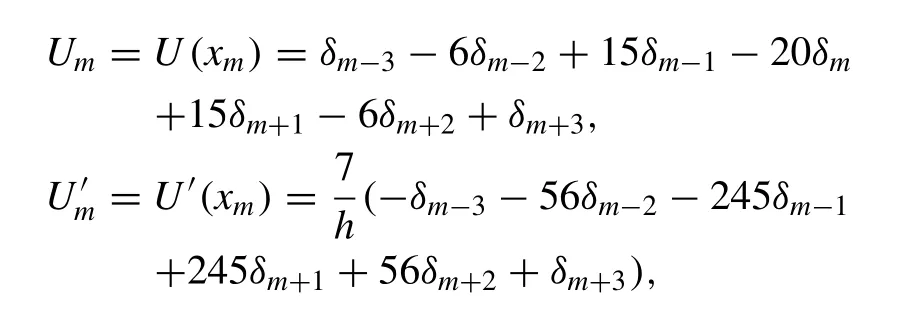

where the symbols′,′′,′′′,iv,vandvidenotes differentiation with respect tox, respectively. The splinesφm(x) and its two principle derivatives vanish outside the interval [xm-4,xm+4] .
3.Collocation fi nite element method
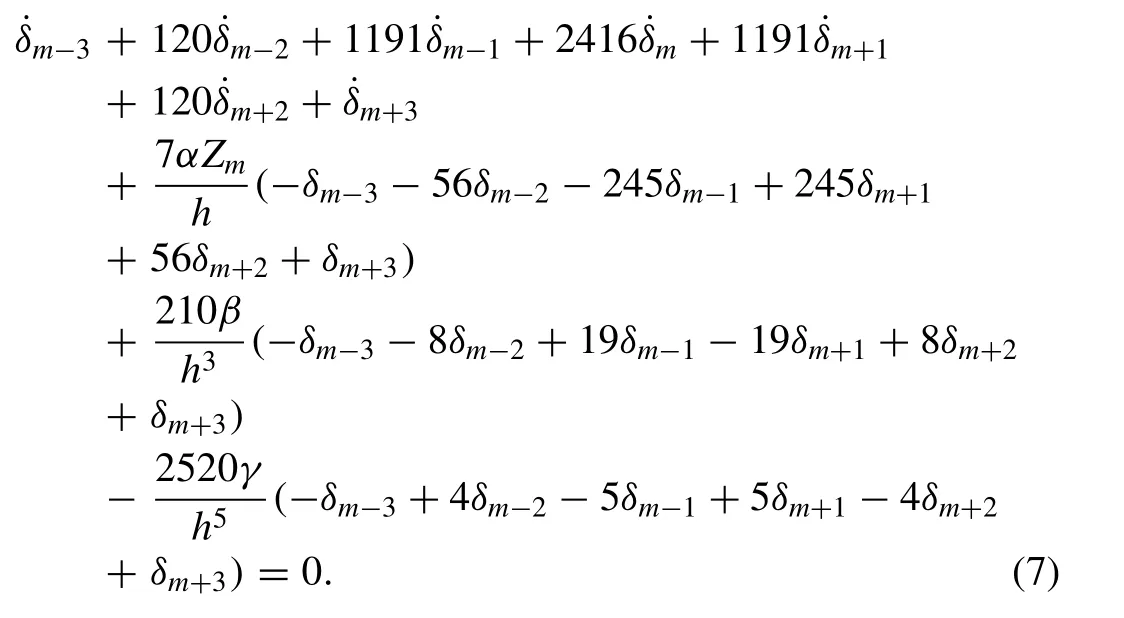
Now, we identify the collocation points with the knots and use Eq. (6) to evaluateUm, its necessary space derivatives and substitute into Eq. (1) to obtain the set of the coupled ordinary differential equations. For the linearization technique we get the following equation:
where
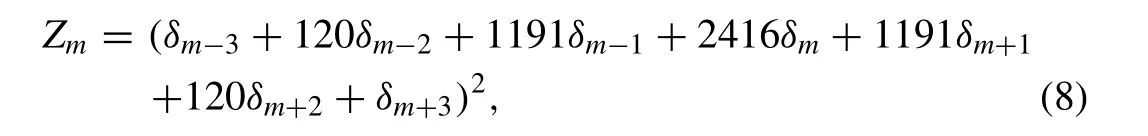
and.denotes derivative with respect to time. If time parametersδi’s and its time derivatives ˙δi’s in Eq. (7) are discretized by the Crank–Nicolson formula and usual fi nite difference approximation, respectively,
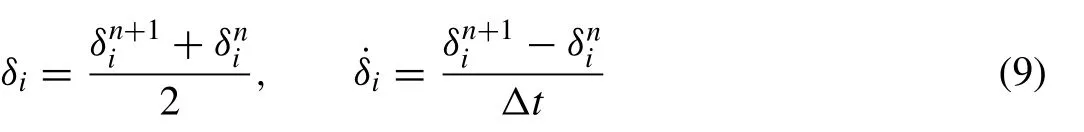
we obtain a recurrence relationship between two time levelsnandn+ 1 relating two unknown parametersfori=m-3,m-2,...,m+ 2,m+ 3
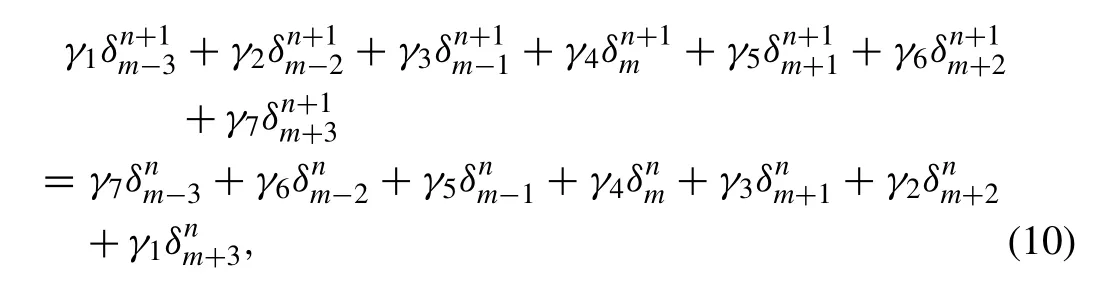
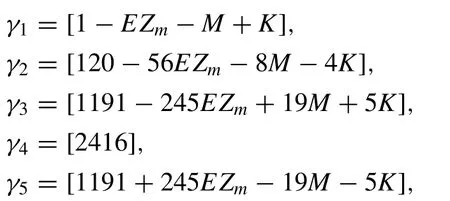
where boundary conditions and can be used to eliminateδ-3,δ-2,δ-1andδN+1,δN+2,δN+3from the system (10) which then becomes a matrix equation for theN+ 1 unknownsd=(δ0,δ1 ,...,δN)Tof the form

The matricesAandBare septa-diagonal(N+ 1)×(N+ 1)matrices and so they are easily solved. Two or three inner iterations are applied to the termat each time step to cope with the non-linearity caused byZm.Before the commencement of the solution process, initial parametersd0must be determined by using the initial condition and following derivatives at the boundaries;
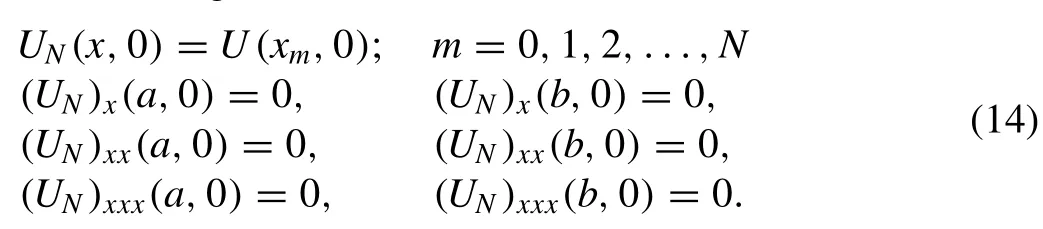
So we have the following matrix form for the initial vectord0;

where

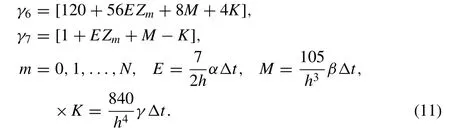
For the linearization technique, the termU2in non-linear termU2Uxis taken as
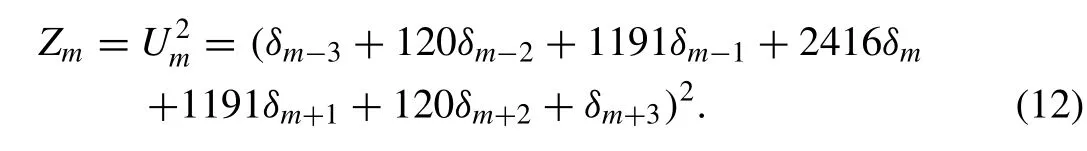
The system (10) consists of(N+ 1)linear equations including(N+ 7)unknown parameters (δ-3,δ-2,δ-1,...,δN+1,δN+2,δN+3)T. To obtain a unique solution to this system, we need six additional constraints. These are obtained from the
4.Stability analysis
The stability analysis is based on the von Neumann theory. The growth factorξof the error in a typical mode of amplitude

wherekis the mode number andhthe element size, is determined from a linearization of the numerical scheme. In order to apply the stability analysis, the Kawahara equation can be linearized by assuming that the quantityU2in the non-linear termU2Uxis locally constant. Substituting the Fourier mode(16) into (10) gives the growth factorξof the form

where

Table 2Invariants and error norms for single solitary wave with α = β = γ = 1 ,h = 0. 1 and Δt = 0. 05 .
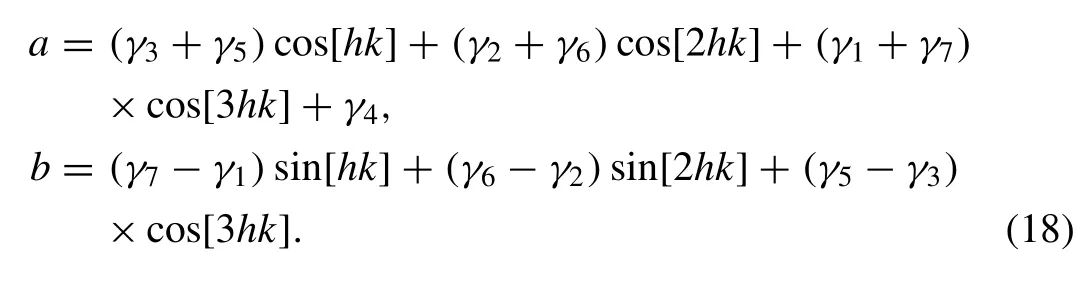
The modulus of |ξ| is 1, therefore the linearized scheme is unconditionally stable.
5.Numerical examples and results
Numerical results of the mKdV equation are obtained for four problems: the motion of single solitary wave, interaction of two and three solitary waves and evolution of solitons. We use the error normL2and the error normL∞
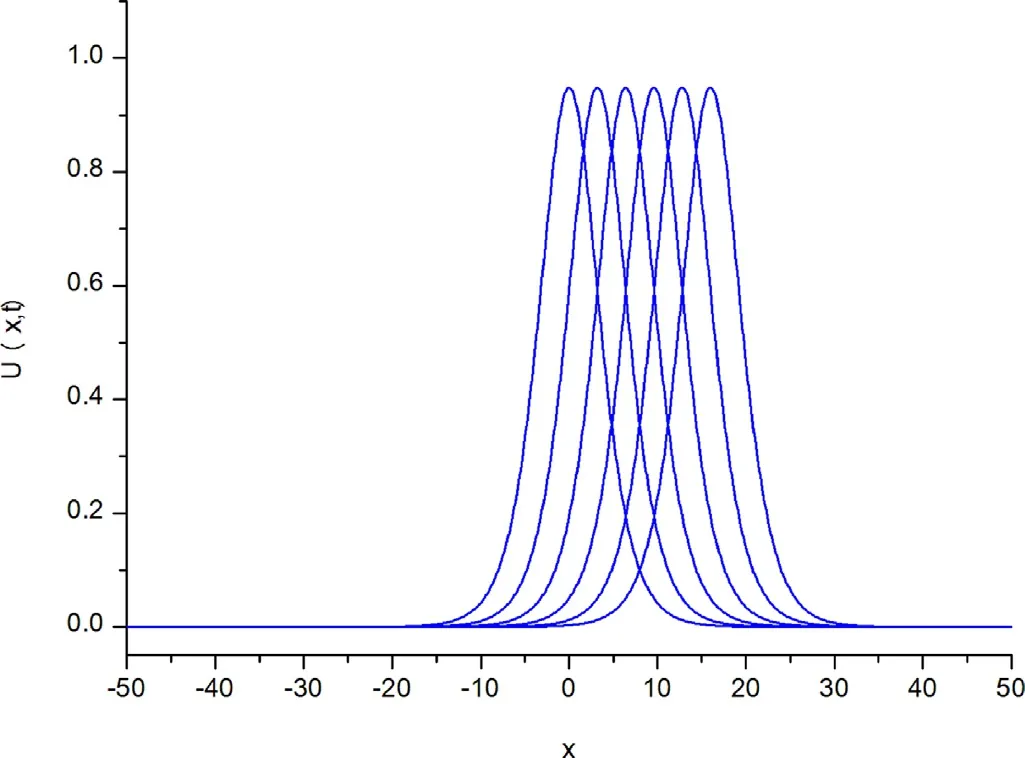
Fig. 1. Single solitary wave pro fi le for α = β = γ = 1 , h = 0. 1 , Δt = 0. 05 and 0 ≤ t ≤ 100.
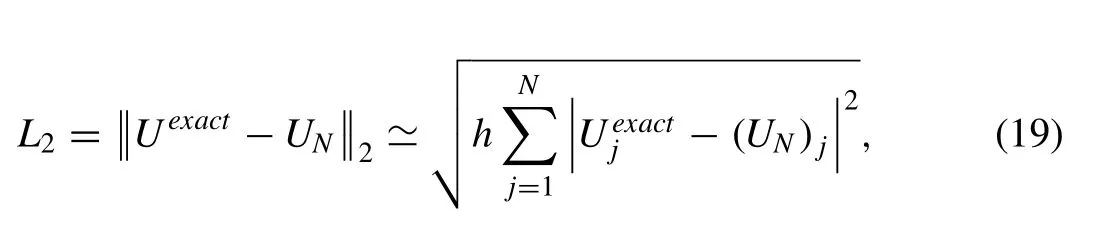
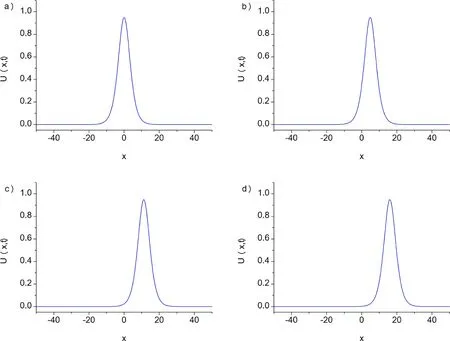
Fig. 2. Motion of the single solitary wave for α = β = γ = 1 , h = 0. 1 and Δt = 0. 05 at a) t = 0, b) t = 30, c) t = 70, d) t = 100.

to calculate the difference between analytical and numerical solutions at some speci fi ed times. Kawahara Eq. (1) possesses only two conservation constants given by

which correspond to conversation of mass and momentum, respectively [30] . In the simulation of solitary wave motion, the invariantsI1andI2are monitored to check the conversation of the numerical algorithm.
5.1. The motion of single solitary wave
The solitary wave solution of the Kawahara Eq. (1) is given by considered with the boundary conditionsU→ 0 asx→ ± ∞ and the initial condition
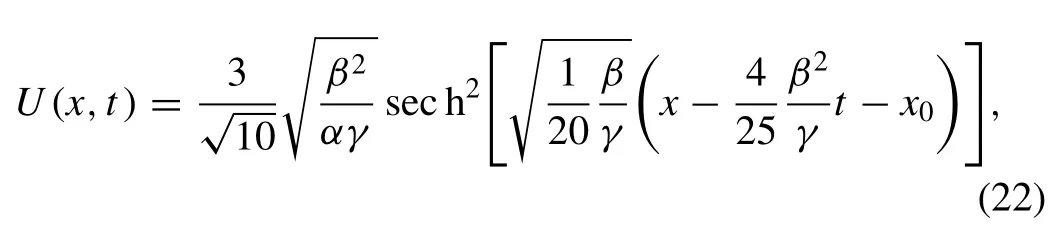
whereα,β,γandx0are arbitrary constants. The initial condition is
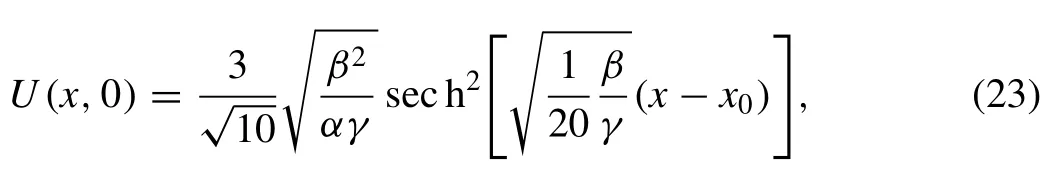
For the numerical simulation of the motion of a single solitary wave, parametersα=β=γ= 1,h= 0.1 andΔt= 0.05 over the interval [ -50,50 ] are chosen. For these parameters, the solitary wave has an amplitude 0.94868. The conserved quantities and error normsL2andL∞are shown at selected times up to timet= 100.The obtained results are tabulated in Table 2 . It can be seen from the Table 2 that the error normsL2andL∞are found to be small enough and the quantities in the invariants remain almost constant during the computer run. Percentage of relative changes ofI1andI2are found to be 1.164 × 10-4%, 6.854 × 10-10%,respectively. In Fig. 1 , the numerical solutions are displayed att= 0,20,40,...,100. The graphs are plotted numerical solution of single soliton withα=β=γ= 1,h= 0.1 andΔt= 0.05 at selected times fromt= 0 tot= 100,in Fig. 2 .Errors distributions at timet= 100 are depicted for solitary waves amplitudes 0.94868 in Fig. 3 to show the errors between the analytical and numerical results over the problem domain.
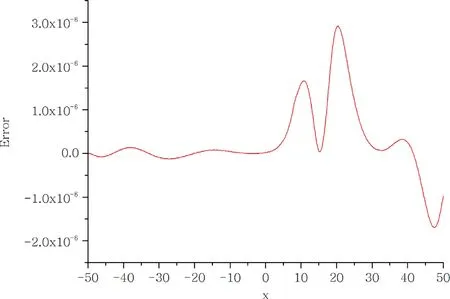
Fig. 3. Error for α = β = γ = 1 , h = 0. 1 and Δt = 0. 05 , at t = 100.
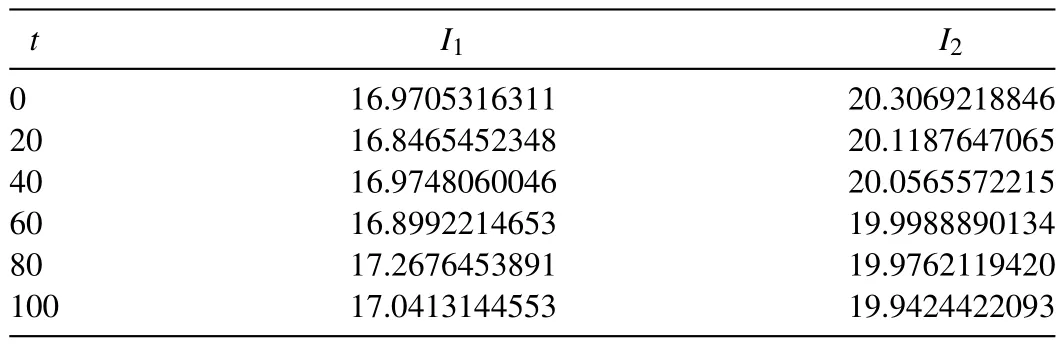
Table 3Comparison of invariants for the interaction of two solitary waves with α=β = γ = 1 , h = 0. 1 , Δt = 0. 05 , c 1 = 0. 85 , c 2 = 0. 35 , x 1 = 0 and x 2 = 20.
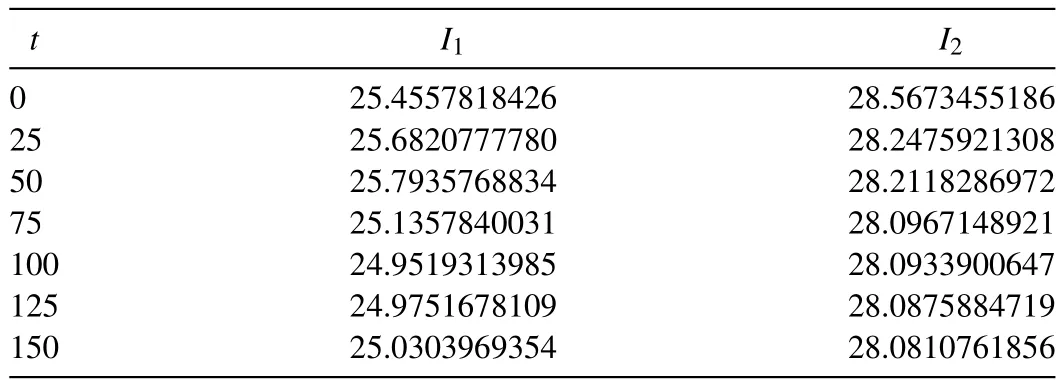
Table 4Comparison of invariants for the interaction of three solitary waves with α = β = γ = 1 , h = 0. 1 , Δt = 0. 05 , c 1 = 0. 85 , c 2 = 0. 50, c 3 = 0. 25 , x 1 =-20, x 2 = 0 and x 3 = 20.

Table 5Invariants for Gaussian initial condition with α = β = γ = 1 and h = Δt =0. 25 at 0 ≤ t ≤ 5.
5.2. Interaction of two solitary waves
Secondly, we consider the interaction of two solitary waves by using the initial condition given by the linear sum of two well separated solitary waves having various amplitudes
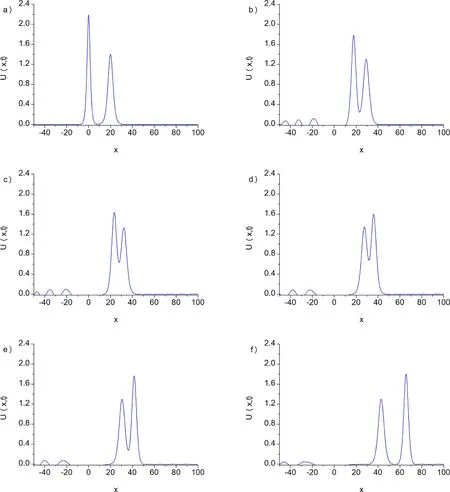
Fig. 4. Interaction of two solitary waves for α = β = γ = 1 , h = 0. 1 , Δt = 0. 05 , c 1 = 0. 85 , c 2 = 0. 35 , x 1 = 0 and x 2 = 20 at a) t = 0, b) t = 30, c) t = 40,d) t = 50, e) t = 60, f) t = 100.
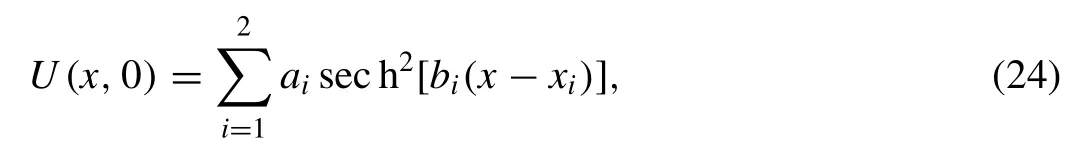
For the simulation, the parametersα=β=γ= 1,h= 0.1,Δt= 0.05,c1 = 0.85,c2 = 0.35,x1 = 0 andx2 =20 are chosen over the range -50 ≤x≤ 100. The experiment are run fromt= 0 tot= 100 and the calculated values of the invariantsI1andI2obtained by the present method are tabulated in Table 3 . It is seen that the obtained values of the invariants remain almost constant during the computer run.
Fig. 4 shows the development of the interaction of two solitary waves. It is clear from the fi gure that, att= 0 the greater solitary wave at the left position of the smaller solitary wave, at the beginning of the run. With the increases of the time the greater solitary wave catches up the smaller until at timet= 30,the smaller solitary wave being absorbed.The overlapping process continues untilt= 60,greater soli-tary wave has overtaken the smaller solitary wave and get in the process of the separating. At timet= 100, the interaction is complete and the greater solitary wave has separated completely.
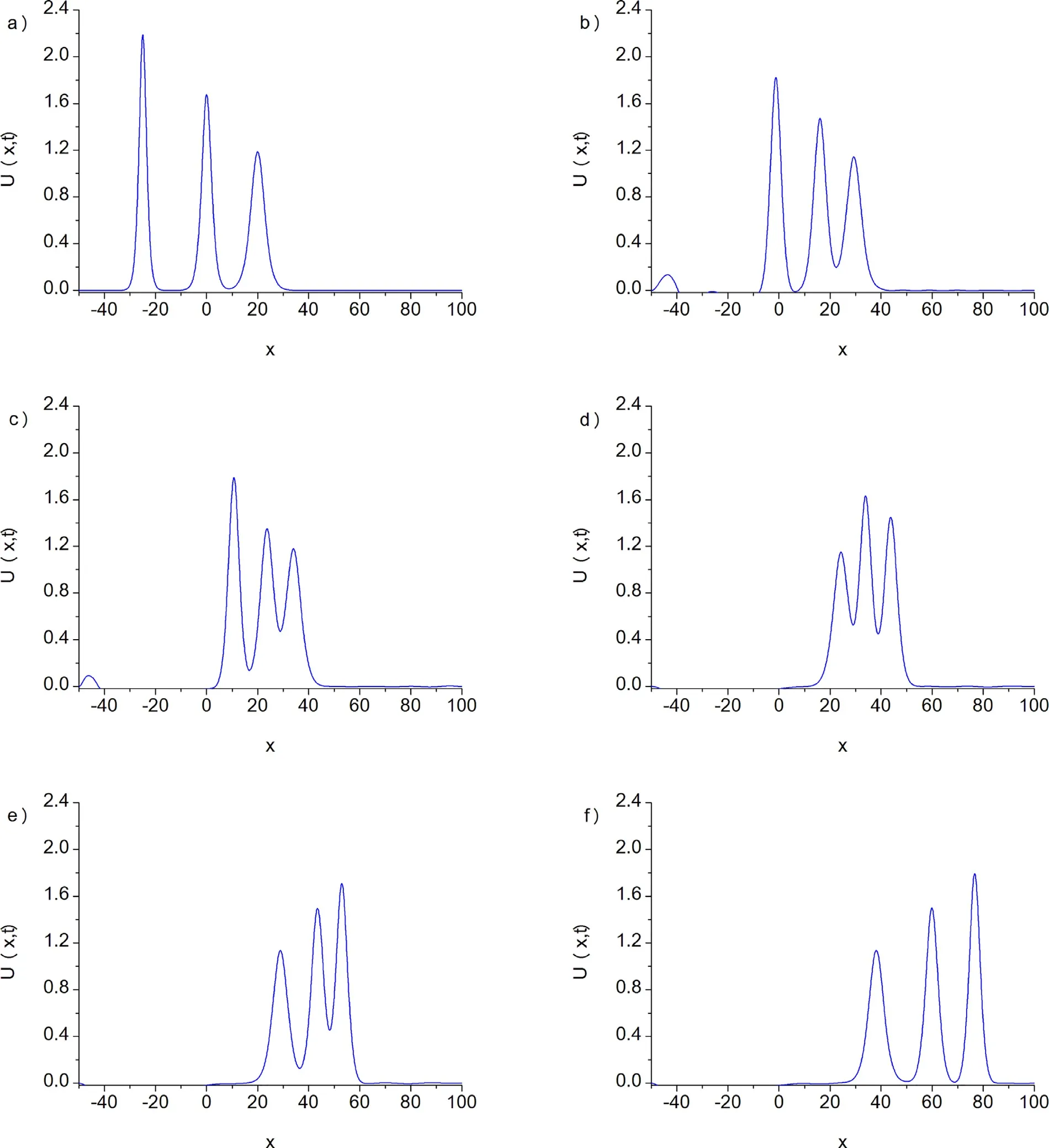
Fig. 5. Interaction of three solitary waves for α = β = γ = 1 , h = 0. 1 , Δt = 0. 05 , c 1 = 0. 85 , c 2 = 0. 50, c 3 = 0. 25 , x 1 = -25 , x 2 = 0 and x 3 = 20 at a)t = 0, b) t = 40, c) t = 60, d) t = 90, e) t = 110, f) t = 150.
5.3. Interaction of three solitary waves
Thirdly, we consider the interaction of three solitary waves by using the initial condition given by the linear sum of three well separated solitary waves having various amplitudes

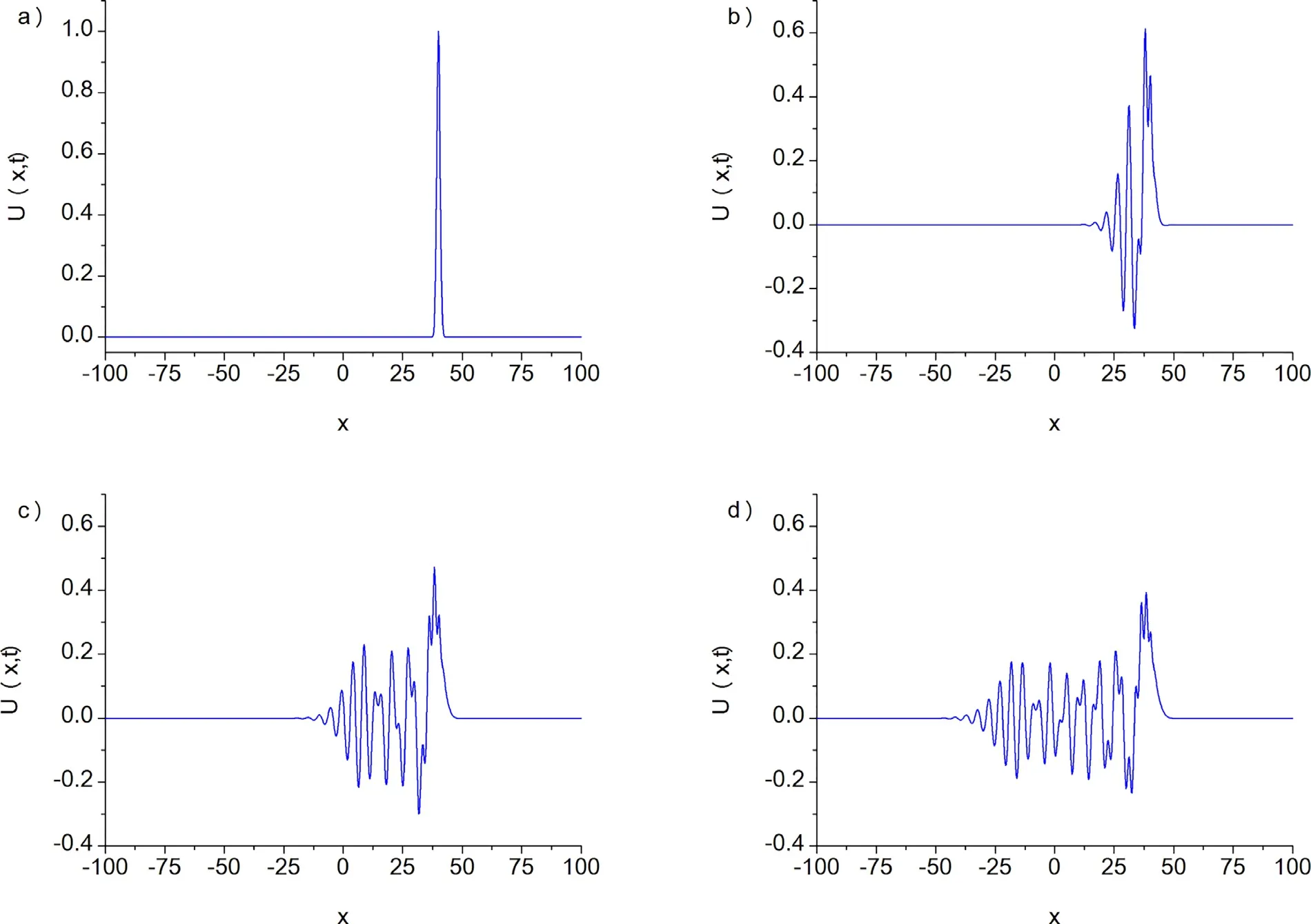
Fig. 6. Evolution of waves for α = β = γ = 1 and h = Δt = 0. 25 at a) t = 0, b) t = 1 , c) t = 3 , d) t = 5 .
For the computational work, the parametersα=β=γ= 1,h= 0.1,Δt= 0.05,c1 = 0.85,c2 = 0.50,c3= 0.25,x1= -25,x2= 0 andx3= 20 are taken over the range -50 ≤x≤ 100. Simulations are done up to timet= 150. Table 4 displays values of the conserved quantities pending the travelling. It is seen from the Table 4 that the obtained values of the invariants remain almost during the computer run. In Fig. 5 , the interaction of three solitary waves is depicted. As it is seen from the Fig. 5 , interaction started about timet= 40,overlapping processes occurred between timet= 40 andt= 110 and waves started to resume their original shapes after the timet= 150.
6.Evolution of solitons
Evolution of a train of solitons of the Kawahara equation has been studied using the Gaussian initial condition
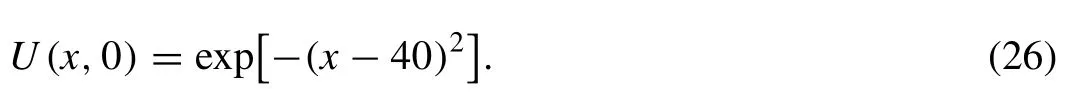
The values ofα=β=γ= 1,h= 0.25 andΔt= 0.25 are chosen at the region of the -100 ≤x≤ 100. The numerical computations are done up tot= 5 . The values of the two invariants of motion are presented in Table 5 . Percentage of relative changes ofI1andI2are found to be 1.782 ×10-8%,4.048 ×10-8%, respectively. As seen in the Fig. 6 , evolution of any soliton doesn’t occur with Gaussian initial condition.However, as time progressed it is observed that the waves made oscillation increasingly.
7.Conclusion
In this paper, we have obtained the solitary wave solutions of the modi fi ed Kawahara equation by using collocation method based on septic B-spline functions. To prove the performance of numerical scheme, the error normsL2,L∞for single solitary wave and two invariantsI1andI2for three test problems have been calculated. It has been observed that the error norms are satisfactorily small and the invariants are well conserved. Also, the linearized numerical scheme is unconditionally stable. The method successfully models the motion and interaction of the solitary waves and evolution of solitons.Finally, we can say that this method can a reliable method for obtaining the numerical solutions of similar type non-linear equations.
Acknowledgment
The author, is grateful to The Scienti fi c and Technological Research Council of Turkey for granting scholarship for Ph.D.studies.
[1] D.J. Korteweg , G. de Vries , Philos. Mag. 39 (1895) 422–443 .
[2] H.N.A. Ismail , K.R. Raslan , G.S.E. Salem , Appl. Math. Comput. 154(1) (2004) 17–29 .
[3] H. Triki , T. Ak , S.P. Moshokoa , A. Biswas , Ocean Eng. 114 (2016)192–203 .
[4] T. Ak , S.B.G. Karakoc , A. Biswas , Iran. J. Sci. Technol. Trans. A Sci.41 (4) (2017a) 1109–1121 .
[5] T. Ak , S.B.G. Karakoc , A. Biswas , Scientia Iranica B 24 (3) (2017b)1148–1159 .
[6] A. Biswas , K.R. Raslan , Phys. Wave Phenom. 19 (2) (2011) 142–147 .
[7] K.R. Raslan , H.A. Baghdady , Int. J. Res. Rev. Appl. Sci. 18 (1) (2014)59–64 .
[8] K.R. Raslan , H.A. Baghdady , Gen. Math. Notes 27 (1) (2015) 101–113 .
[9] L. Girgis , E. Zerrad , A. Biswas , Int. J. Ocean. Oceanogr. 4 (1) (2010)45–54 .
[10] A.-M. Wazwaz , Commun. Nonlinear Sci. Numer. Simul. 10 (8) (2005)855–867 .
[11] A. Biswas , Commun. Nonlinear Sci. Numer. Simul. 15 (10) (2010)2744–2746 .
[12] A.-M. Wazwaz , H. Triki , Commun. Nonlinear Sci. Numer. Simul. 16(3) (2011) 1122–1126 .
[13] A.-M. Wazwaz , Commun. Nonlinear Sci. Numer. Simul. 13 (5) (2008)889–901 .
[14] E.V. Krishnan , S. Kumar , A. Biswas , Nonlinear Dyn. 70 (2012)1213–1221 .
[15] T. Ak , S. Dhawan , S.B.G. Karakoc , S.K. Bhowmik , K.R. Raslan , Math.Modell. Anal. 22 (3) (2017) 373–388 .
[16] T. Ak , S.B.G. Karakoc , H. Triki , Eur. Phys. J. Plus 131 (10) (2016)356–370 .
[17] A. Biswas , E.V. Krishnan , P. Suarez , A.H. Kara , S. Kumar , Indian J.Phys. 87 (2) (2013) 169–175 .
[18] A. Biswas , M.S. Ismail , Appl. Math. Comput. 216 (12) (2010)3662–3670 .
[19] H. Triki , A.H. Kara , A.H. Bhrawy , A. Biswas , Acta Physica Polonica A 125 (5) (2014) 1099–1107 .
[20] H. Zareamoghaddam , Middle-East J. Sci. Res. 7 (6) (2011) 1061–1064 .
[21] A.-M. Wazwaz , Appl. Math. Comput. 145 (1) (2003) 133–150 .
[22] M. Haragus , E. Lombardi , A. Scheel , J. Math. Fluid Mech. 8 (2006)482–509 .
[23] A.-M. Wazwaz , Phys. Lett. A 360 (4–5) (2007) 588–592 .
[24] A. Biswas , Appl. Appl. Math. 3 (2) (2008) 218–223 .
[25] A. Biswas , E. Zerrad , Adv. Stud. Theor. Appl. Mech. 1 (1) (2008a)39–44 .
[26] A. Biswas , E. Zerrad , Fizika A 17 (3) (2008b) 103–108 .
[27] A. Biswas , Appl. Math. Lett. 22 (2) (2009) 208–210 .
[28] S.B.G. Karakoc , H. Zeybek , T. Ak , Stat. Optim. Inf. Comput. 2 (2014)211–221 .
[29] P.M. Prenter , Splines and Variational Methods, John Wiley, New York,1975 .
[30] R.P. Malik , On Fifth Order KdV Type Equation, Bogoliubov Laboratory of Theoretical Physics, Joint Institute for Nuclear Research, Moscow,1997 .
 Journal of Ocean Engineering and Science2018年1期
Journal of Ocean Engineering and Science2018年1期
- Journal of Ocean Engineering and Science的其它文章
- Thenewtypesofwavesolutionsofthe Burger’s equationandthe Benjamin–Bona–Mahonyequation
- Multiple soliton solutionsforthe(3+1)conformable space–time fractional modi fi edKorteweg–de-Vriesequations
- Coupled boundary element methodand fi nite element methodfor hydroelasticanalysisoffl oatingplate
- Fuzzyfaulttree analysisofoilandgas leakagein subseaproduction systems
- Onanalyticalsolutionofsystemof nonlinear fractional boundaryvalue problemsassociatedwithobstacle
- RiskassessmentofLNGandFLNGvessels during manoeuvringinopen sea
