Electron Acceleration by Beating of Two Intense Cross-Focused Hollow Gaussian Laser Beams in Plasma?
Saleh T.Mahmoud,Rakhi Gauniyal,Na fis Ahmad,Priyanka Rawat,and Gunjan Purohit
1Department of Physics,College of Science,UAE University,P.O.Box 15551 Al-Ain,United Arab Emirates
2Laser Plasma Computational Laboratory,Department of Physics,DAV(PG)College,Dehradun,Uttarakhand-248001,India
1 Introduction
Laser driven plasma-based accelerators are of great interest because of their ability to sustain extremely large acceleration gradients.[1?4]They have widespread applications in various fields such as particle physics,materials science,medicine(ranging from x-ray diagnostics to particle beam therapies),manufacturing industry and to produce extremely short electron bunches.In laser plasma interaction,various schemes are operative for particle acceleration such as laser wake field accelerator(LWFA),[5?7]plasma beat wave accelerator(PBWA),[5,8]multiple laser pulses,[9?10]self-modulated LWFA[11?12]etc.in which very high intense laser beams are used.The key requirement for achieving higher acceleration is the large amplitude of the electron plasma wave.A large amplitude plasma wave(with phase velocity near the speed of light)is driven by intense laser pulse in which plasma electrons can be trapped and accelerated to relativistic energies.Therefore,the excitation of electron plasma wave by intense laser beams in plasmas has been an active field of research for charged particle acceleration.
There has been signi ficant interest in the beat wave excitation of electron plasma wave and its application in plasma based particle accelerators.The plasma beat-wave accelerator scheme is one of the most mature methods for plasma acceleration in laser plasma interaction.[5]In this scheme,two intense laser beams of slightly different frequenciesω1&ω2and corresponding wave numbersk1&k2are used to resonantly excite an electron plasma wave.The resonance conditions for beat wave excitation of electron plasma wave are:and.If the beat frequency?ωis close to the plasma frequencyωp0,a very large amplitude relativistic electron plasma wave can be generated,which can be used to accelerate electrons efficiently to high energies in short distances.In this process,self-focusing of an intense laser beam in plasmas plays an important role and arises due to increase of the on-axis index of refraction relative to the edge of the laser beam.When two intense laser beams with slightly different frequencies simultaneously propagates in plasma,self-focusing of one laser beam is affected by the self-focusing of another laser beam.Due to mutual interaction of two laser beams,cross-focusing takes place in plasma.This method is used to generate large amplitude electron plasma wave for ultrahigh gradient electron acceleration in PBWA scheme.A lot of theoretical and experimental work has been reported on the excitation of electron plasma wave and electron acceleration by beating of two laser beams in plasma.[5,13?37]
It has been observed that the focusing of laser beams in plasma and the yield of electron acceleration depends on the spatial pro file of laser beams and the nonlinearities associated with plasma.Most of the earlier investigations on excitation of electron plasma wave and electron acceleration have been carried out by taking Gaussian intensity distribution of laser beams with ponderomo-tive/relativistic nonlinearity.In contrast with Gaussian pro file of laser beams,currently,the hollow Gaussian intensity pro file of laser beams with minimum field intensity at the center has attracted much more attentions because of their unique physical properties and applications.[38?40]The main feature of considered hollow Gaussian laser beams is having the same power at different beam orders with null intensity at the centre.The propagation dynamics of hollow Gaussian beams(HGBs)have been widely studied both experimentally and theoretically.[41?46]Various techniques[47?50]have been used to generate HGBs.These beams can be expressed as a superposition of a series of Lagurerre-Gaussian modes.[41]Moreover,when an ultra-intense laser beams propagates in plasma,both relativistic and ponderomotive nonlinearities arise simultaneously due to electron mass variation and electron density perturbations respectively,which depend on the time scale of the laser pulse.[51?52]Therefore,in comparison with only relativistic/ponderomotive nonlinearity,the dynamics of the propagation of laser beams in plasma is expected to be drastically affected by cumulative effects of relativistic-ponderomotive nonlinearity.It is also important to mention that the relativistic effect and ponderomotive nonlinearity contribute to focusing on a femtosecond time scale at very high intensity.Cross-focusing of HGBs with relativistic/ponderomotive or relativisticponderomotive nonlinearities in plasma have been investigated in detail[53?55]but no one has studied the excitation of EPW and electron acceleration. Moreover,donut wake fields generation for particle acceleration by Laguerre-Gaussian laser pulses(carrying a finite amount of orbital angular momentum)using particle-incell simulations have also been reported in under-dense plasma.[56?57]
In the present study,we have considered the propagation of two intense hollow Gaussian beams in collisionless plasma.The intensity distribution of the beams along the axis is zero and the maximum is away from the axis.We have studied the cross-focusing of two intense hollow Gaussian laser beams in collisionless plasma with relativistic and ponderomotive nonlinearities and further its effect on the excitation of EPW and electron acceleration.The paraxial-ray approximation[58?59]is used to describe the focal region of the laser beam where all the relevant parameters correspond to a narrow range around the maximum irradiance of the HGBs.Section 2 presents the relativistic-ponderomotive focusing of two HGBs in plasma under paraxial-ray approximation.The effect of the cross-focusing of the HGBs on the excitation of the electron plasma wave and electron acceleration is studied in Sec.3.Section 4 deals with the results and discussion.The conclusions drawn from the results of present investigation have been summarized in Sec.5.
2 Propagation of Hollow Gaussian Laser Beams in Collisional Plasma
We consider two intense linearly polarized co-axial hollow Gaussian laser beams of frequenciesω1andω2propagating along thez-direction in the collisional plasma.The initial electric field distribution of the beams are given by
whereris the radial coordinate of the cylindrical coordinate system,r10andr20are the initial spot size of the laser beams,E10andE20are the amplitude of HGBs maximumnis the order of the HGBs(n=0 corresponds to the fundamental Gaussian laser beam)and a positive integer,characterizing the shape of the HGBs an position of its irradiance maximum.
For hollow Gaussian laser beams,transforming the(r,z)coordinate in to(η,z)coordinate by the relation[44]
whereηis a reduced radial coordinate,f1,2is the beam width of HGBs,r=r10,20f1,2(2n)1/2is the position of the maximum irradiance for the propagating beams.Most of the power of HGBs are concentrated in the region aroundη=0.
The ponderomotive force acting on the electrons in the presence of relativistic nonlinearity is given by[52?53]
This force modi fies the background electron density because electrons are expelled away from the region of higher electric field.The modi fied electron density(nd)due to relativistic-ponderomotive force is given as[52]
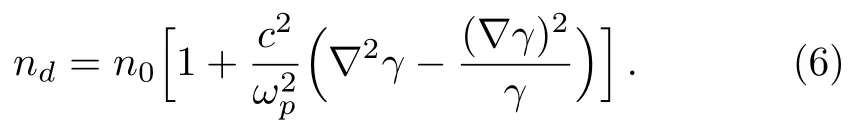
Using Eq.(3)into Eq.(7),the total electron density can be written as
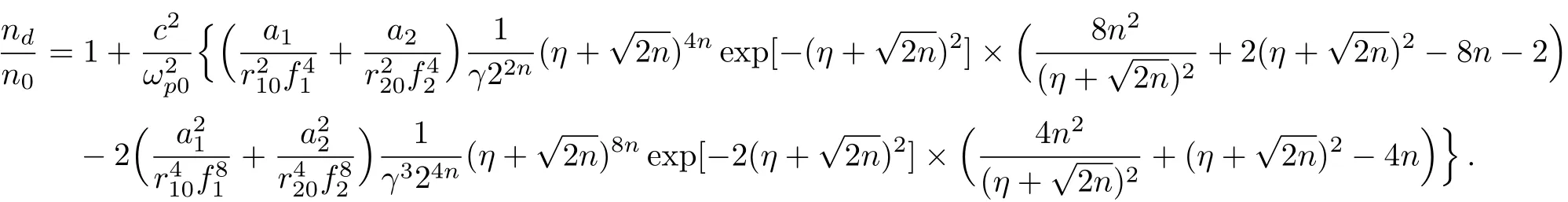
Hereare the intensities of first and second laser beams.
The dielectric constant of the plasma is given by
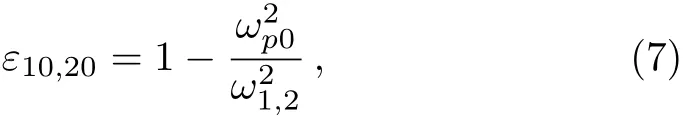
whereis the plasma frequency witheis the charge of an electron,m0is its rest mass,andn0is the density of plasma electrons in the absence of laser beam.The effective dielectric constant(?1,2)of the plasma(in the presence of relativistic-ponderomotive nonlinearity)at frequenciesω1andω2respectively is given by

where?10,20is the linear part of dielectric constant of the plasma.The dielectric constant may be expended around the maximum of HGBs i.e.atη=0.For HGBs,one can express the dielectric constant?1,2(η,z),in terms of?1,2(r,z).Expanding dielectric constant aroundη=0 by Taylor expansion,one can write
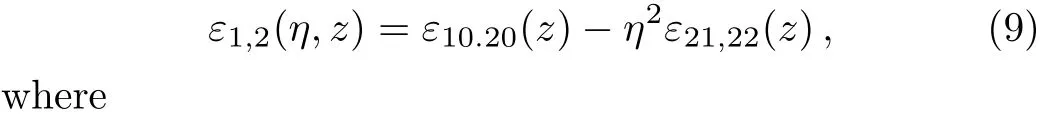


3 Beat Wave Excitation of Plasma Wave and Electron Acceleration
Due to beating of two hollow Gaussian laser beams in plasma and modi fication in plasma density via relativisticponderomotive force,electron plasma wave(EPW)is generated.In this process,the contribution of ions is negligible because they only provide a positive background,i.e.,only plasma electrons are responsible for excitation of EPW.The amplitude of electron plasma wave(which depends on the background electron density)gets strongly coupled to the laser beams.To study the effect of relativistic and ponderomotive nonlinearities on the generation of the plasma wave by the beat wave process in paraxial region,we start with the following fluid equations:
(i)The continuity equation:

Equation(26)contains two plasma waves(both have different frequencies).The first one is supported by hot plasma and the second by the source term at the different frequency.Ifωp0/?ω≤1,the phase velocity is almost equal to the thermal velocity of the electron and Landau damping occur.But asωp0/?ω≈1,the phase velocity is very large as compared to the electron thermal velocity and Landau damping is negligible.The solution of Eq.(9)with in the WKB approximation can be expressed as
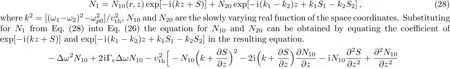

The power associated with electron wave is given by[29]
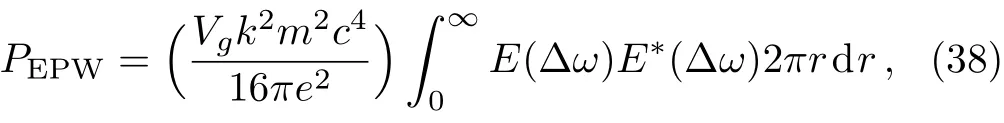
whereis the group velocity.Equation(38)has been solved numerically with the help of Eqs.(21),(36),and(37).
The excited electron plasma wave transfers its energy to accelerate the electrons at the difference frequency of laser beams.The equation governing electron momentum
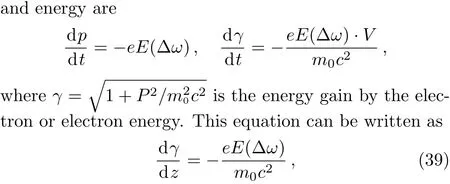
whereE(?ω)is given by Eqs.(37)and(39)gives the electron energy.Equation(39)has been solved numerically,where we have usedf1andf2by Eq.(21).
4 Numerical Results and Discussion
In order to study the cross-focusing of two intense hollow Gaussian laser beams in collisonal plasma with dominant relativistic-ponderomotive nonlinearity and its effect on the generation of electron plasma wave and electron acceleration in paraxial-ray approximation,numerical computation of Eqs.(19),(21),(38),and(39)has been performed for the typical laser plasma parameters.The following set of the parameters has been used in the numerical calculation:ω1=1.776×1015rad/s,ω2=1.716×1015rad/s,r1=15μm,r2=20μm,ωp0=0.3ω2,a1=3,a2=2,2.4,2.8,andn=1,2,3.For initial plane wave fronts of the beams,the initial conditions forf1,2aref1,2=1 and df1,2/dz=0 atz=0.
When two intense hollow Gaussian laser beams of slightly different frequencies simultaneously propagate through the plasma,the background electron density of plasma is modi fied due to ponderomotive force.Equation(19)describes the intensity pro file of HGBs in plasma along the radial direction in presence of relativistic and ponderomotive nonlinearities,while Eq.(21)determines the focusing/defocusing of the hollow Gaussian beams along the distance of propagation in the plasma,where the first term on the right hand side shows the diffraction behaviour of laser beams and remaining terms on the right hand side show the converging behaviour that arises due to the relativistic and ponderomotive nonlinearity.The focusing/defocusing behaviour of laser beams depends on the magnitudes of the nonlinear coupling terms.It is clear from Eq.(19),the intensity pro file of both laser beams depends on the focusing/defocusing of the laser beams i.e.beam width parametersf1,2.
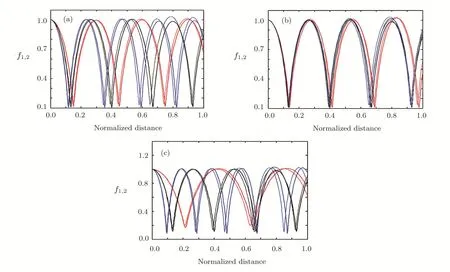
Fig.1 (Color online)Variation of the beam width parameters(f1and f2)with the normalized distance of propagation(ξ)of first and second HGBs:(a)For different orders of n(red,black and blue colors are for n=1,2 and 3)with a1=3,a2=2.4 and ωp0=0.3ω2.(b)For different values of a2(red,black,and blue colors are for a2=2,2.4,2.8)with a1=3,n=2 and ωp0=0.3ω2.(c)For different values of ωp0(red,black,and blue colors are for ωp0=0.2ω2,0.3ω2,and 0.4ω2)with a1=3,a2=2.4.and n=2,respectively,when relativistic and ponderomotive nonlinearities are operative.The solid line represents f1and the dotted line represents f2.
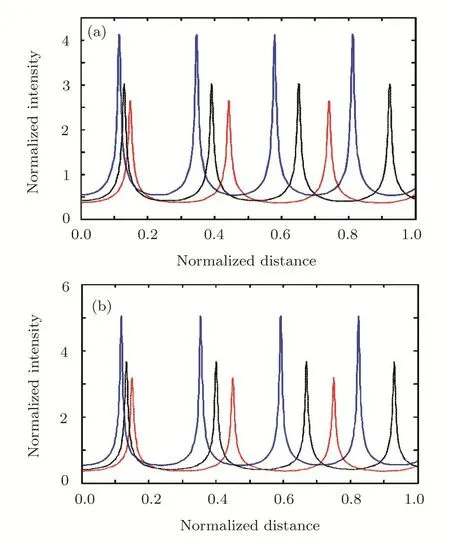
Fig.2 (Color online)Variation of the normalized intensity of HGBs with the normalized distance of propagation(ξ)for different orders of n(red,black and blue colors are for n=1,2 and 3)keeping a1=3,a2=2.4,ωp0=0.3ω2,when relativistic and ponderomotive nonlinearities are operative.(a)and(b)are for first and second laser beam.
The results of Eqs.(19)and(21)are presented in Figs.1 and 2 respectively.Figures 1(a)–1(c)illustrate the focusing behavior of two hollow Gaussian laser beams in plasma with normalized distance of propagation.It is clear that both of the beams show oscillatory self focusing.One can see from Fig.1(a)as the order of the hollow Gaussian beam(n)increases focusing of both beams also increases,which implies that with the increase innthe hollow space across the beam also increases.It is observed from Figs.1(b)and 1(c)that with an increase in the intensity of incident laser beam and plasma density there is an increase in the extent of self-focusing of both the laser beams.This is due to the fact that with an increase in plasma density the number of electrons contributing to the pondermotive-relativistic nonlinearity also increases.These results indicate that focusing of one beam is signi ficantly affected by the presence of another beam.Figures 2(a)and 2(b)represent the normalized intensity of first and second laser beam in plasma respectively along with the normalized distance of propagation for different n.It is observed from the figures that with an increase inn,normalized intensity of both laser beams also increases.It has also been observed that the intensity of laser beams is higher at higher plasma density and incident laser beam intensity(results not shown here).This is due to the strong focusing of both HGBs at higher values ofnand plasma density respectively.Such kind of highly self-focused intense laser beams interact with each other and generate large amplitude electron plasma wave.
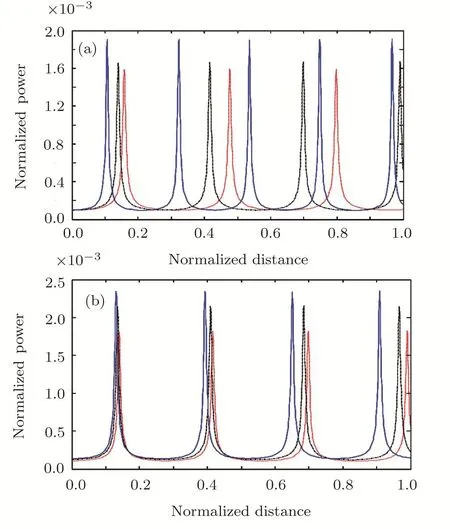
Fig.3(Color online)Variation of the normalized power(P)of electron plasma wave with normalized distance(ξ):(a)For different orders of n(red,black and blue colors are for n=1,2 and 3)with a1=3,a2=2.4,and ωp0=0.3ω2.(b)For different values of a2(red,black,and blue colors are for a2=2,2.4,2.8)with a1=3,n=2,and ωp0=0.3ω2,respectively,when relativistic and ponderomotive nonlinearities are operative.
To see the effect of cross-focusing of two intense hollow Gaussian laser beams on the generation of electron plasma wave,we have studied the excitation of the electron plasma wave by the beat wave process in the presence of relativistic and ponderomotive nonlinearities.It is important to mention here that beating between two copropagating intense laser beams in plasma can generate a longitudinal electron plasma wave with a high electric field and a relativistic phase velocity.The beat plasma wave is very efficient for electron acceleration up to ultrarelativistic energies.Equation(38)describes the normalized power of electron plasma wave generated as a result of beating of the two laser beams.It is evident from Eq.(38),the power of electron plasma wave depends upon the focusing of laser beams in plasma(f1,2),focusing of electron plasma wave(fp)and the electric field associated with electron plasma waveE(?ω).The same set of parameters has been used for numerical calculations as in Figs.1–2.Figures 3(a)and 3(b)show the effect of changing the order of HGBs and the initial intensity of second laser beam(a2)on the power of generated electron plasma wave,at the position of optimum irradiance of the beams(η=0).By increasing laser beam orders and the intensity of second laser beam,the power of generated electron plasma wave increases.This is because the power of generated electron plasma wave depends on the focusing behaviour of laser beams(f1,2),fpand intensity of laser beams.
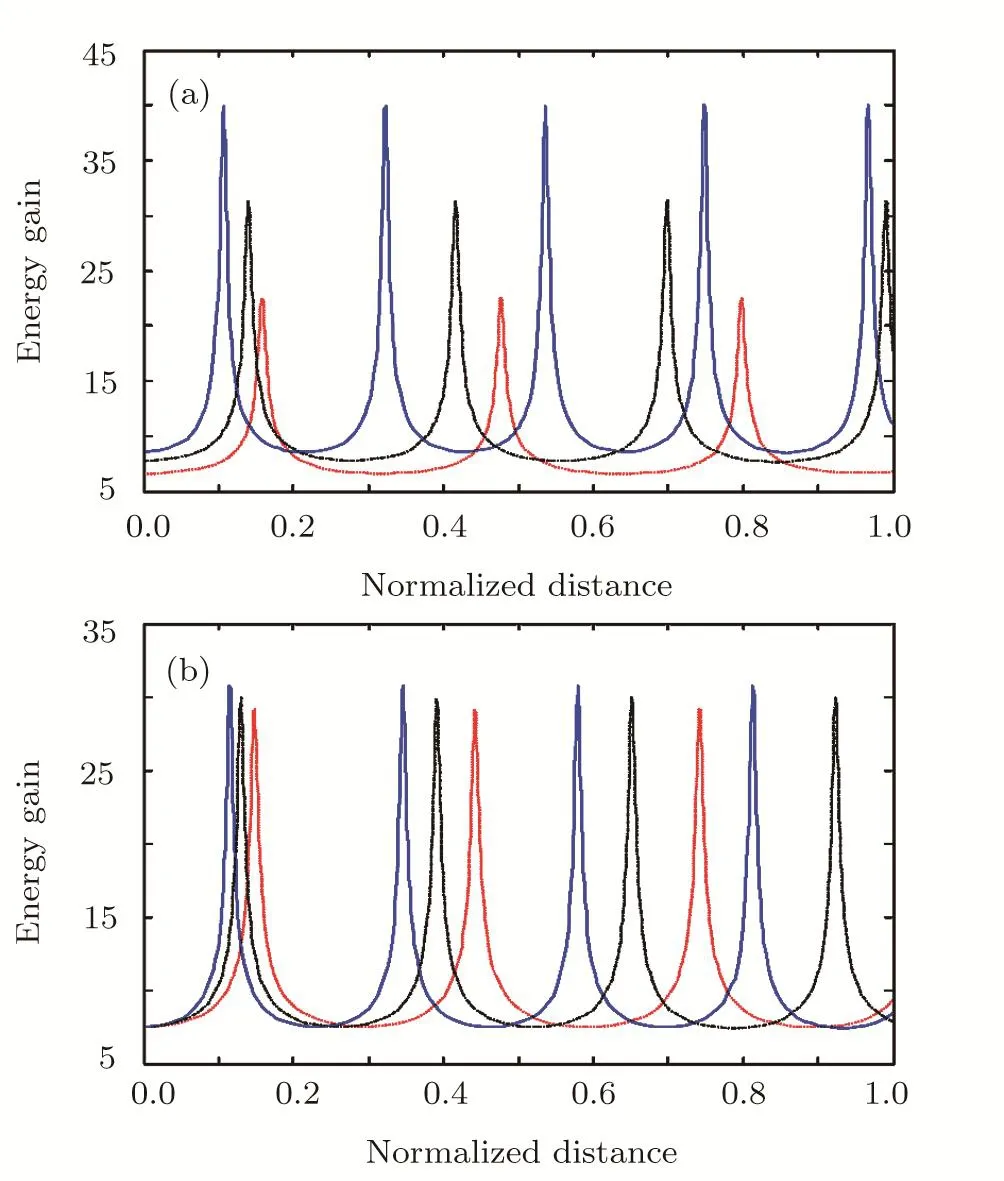
Fig.4(Color online)Variation of the(γ)of the electron with normalized distance(ξ):(a)For different orders of n(red,black and blue colors are for n=1,2 and 3)with a1=3,a2=2.4,and ωp0=0.3ω2.(b)For different values of a2(red,black,and blue colors are for a2=2,2.4,2.8)with a1=3,n=2,and ωp0=0.3ω2,respectively,when relativistic and ponderomotive nonlinearities are operative.
The large amplitude electron plasma wave can be used to accelerate the electrons in plasma beat wave accelerator scheme.Equation(39)gives the expression for energy gain by the electrons.This equation has been solved numerically with the help of Eq.(37)i.e.energy gain depends on the electric field associated with excited electron plasma wave.Figures 4(a)and 4(b)respectively illustrate the effect of changing the value ofnand the intensity of second laser beam(a2)on energy gain by the electrons.These figures clearly indicate that the maximum energy gain by electrons is signi ficantly increased by increasing the value ofbanda2.Although,the nature of these results are similar to Figs.3(a)and 3(b)due to the same reasons as discussed above.Thus,we see that cross-focusing of laser beams plays a crucial role for efficient generation of electron plasma wave and electron acceleration.
5 Conclusions
In conclusion,plasma wave generation and electron acceleration by beating of two intense HGBs in collisionless plasma with dominant relativistic-ponderomotive nonlinearity has been discussed.Paraxial-ray approximation has been used to establish the given formulation.Effects of laser and plasma parameters on the focusing of two HGBs in plasma at difference frequency,generation of electron plasma wave and particle acceleration process is examined.Following conclusions are made from the results:
(i)The order of the hollow Gaussian laser beams plays an important role in plasma beat wave accelerator scheme.
(ii)Focusing of both hollow Gaussian laser beams in plasma is enhanced by increasing the laser beam orders,incident laser intensity,and plasma density.
(iii) The intensity of both laser beams in plasma is higher for higher orders of the HGBs.
(iv)Maximum power of generated electron plasma wave depends on the extent of focusing of laser beams in plasma and the electric field associated with electron plasma wave respectively.
(v)The power of electron plasma wave increases by increasing the laser beam orders and the initial intensity of second/ first laser beams.
(vi)The maximum energy gain also depends on the electric field associated with electron plasma wave and increases by increasing the laser beam orders and the initial intensity of second/ first laser beams.
The results of the present investigation are relevant to laser beat wave based particle accelerators,terahertz generation and in other applications requiring multiple laser beams.
[1]S.M.Hooker,Nature Photonics 7(2013)775.
[2]E.Esarey,C.B.Schroeder,and W.P.Leemans,Rev.Mod.Phys.81(2009)1229.
[3]V.Malka,J.Faure,Y.A.Gauduel,et al.,Nature Physics 4(2008)447.
[4]R.Bingham,Phil.Trans.R.Soc.A.364(2006)559.
[5]T.Tajima and J.M.Dawson,Phys.Rev.Lett.43(1979)267.
[6]A.Pukhov and J.Meyer-ter-vehn,Appl.Phys.B 74(2002)355.
[7]F.Albert,A.G.R.Thomas,S.P.D.Mangles,et al.,Plasma Phys.Control.Fusion 56(2014)084015.
[8]C.V.Filip,R.Narang,S.Ya.Tochitsky,et al.,Phys.Rev.E 69(2004)026404.
[9]K.Nakajima,Phys.Rev.A 45(1992)1149.
[10]D.Umstadter,E.Esarey,and J.Kim,Phys.Rev.Lett.72(1994)1224.
[11]W.P.Leemans,P.Catravas,E.Esarey,et al.,Phys.Rev.Lett.89(2002)174802.
[12]W.Chen,T.Chien,C.Lee,et al.,Phys.Rev.Lett.92(2004)075003.
[13]M.N.Rosenbluth and C.S.Liu,Phys.Rev.Lett.29(1972)701.
[14]C.Joshi,W.B.Mori,T.Katsouleas,et al.,Nature(London)311(1984)525.
[15]Y.Kitagawa,T.Matsumoto,T.Minamihata,et al.,Phys.Rev.Lett.68(1992)48.
[16]C.M.Tang,P.Sprangle,and R.N.Sudan,Appl.Phys.Lett.45(1984)375.
[17]A.Modena,Z.Najmudin,A.E.Dangor,et al.,Nature(London)377(2002)606.
[18]C.E.Clayton,C.Joshi,C.Darrow,and D.Umstadter,Phys.Rev.Lett.54(1985)2343.
[19]N.A.Ebrahim,P.Lavigne,and S.Aithal,IEEE Trans.Nucl.Sci.32(1985)3539.
[20]C.E.Clayton,K.A.Marsh,A.Dyson,et al.,Phys.Rev.Lett.70(1993)37.
[21]M.Everett,A.Lal,D.Gordon,et al.,Nature(London)368(1994)527.
[22]N.A.Ebrahim,J.Appl.Phys.76f50(1994)7645.
[23]F.Amirano ff,D.Bernard,B.Cros,et al.,Phys.Rev.Lett.74(1995)5220.
[24]A.Ghizzo,P.Bertrand,J.Lebas,et al.,Phys.Plasmas 5(1998)4044.
[25]S.Y.Tochitsky,R.Narang,C.V.Filip,et al.,Phys.Rev.Lett.92(2004)095004.
[26]C.V.Filip,R.Narang,S.Ya.Tochitsky,et al.,Phys.Rev.E 69(2004)026404.
[27]B.Walton,Z.Najmudin,M.S.Wei,et al.,Phys.Plasmas 13(2006)013103.
[28]S.Kalmykov,S.A.Yi,and G.Shvets,Plasma Phys.Control.Fusion 51(2009)024011.
[29]D.N.Gupta,M.Singh,and H.Suk,J.Plasma Phys.81(2015)905810324.
[30]A.Singh and N.Gupta,Phys.Plasmas 22(2015)062115.
[31]M.S.Sodha,Govind,D.P.Tewari,et al.,J.Appl.Phys.50(1979)158.
[32]S.T.Mahmoud,H.D.Pandey,and R.P.Sharma,J.Plasma Phys.69(2003)45.
[33]P.Chauhan,S.T.Mahmoud,R.P.Sharma,and H.D.Pandey,J.Plasma Phys.73(2007)117.
[34]G.Purohit,P.K.Chauhan,and R.P.Sharma,Phys.Scr.77(2008)065503.
[35]M.K.Gupta,R.P.Sharma,and V.L.Gupta,Phys.Plasmas 12(2005)123101.
[36]R.P.Sharma and P.K.Chauhan,Phys.Plasmas 15(2008)063103.
[37]P.Rawat,R.K.Singh,R.P.Sharma,and G.Purohit,Eur.Phys.J.D 68(2014)57.
[38]J.Yin,W.Gao,and Y.Zhu,Progress in Optics 44(2003)119.
[39]Y.Yuan,Y.Cai,J.Qu,et al.,Opt.Express 17(2009)17344.
[40]X.Xu,Y.Wang,and W.Jhe,J.Opt.Soc.Am.B 17(2002)1039.
[41]Y.Cai,X.Lu,and Q.Lin,Opt.Lett.28(2003)1084.
[42]Y.Cai and Q.Lin,J.Opt.Soc.Am.A 21(2004)1058.
[43]Z.Mei and D.Zhao,J.Opt.Soc.Am.A 22(2005)1898.
[44]M.S.Sodha,S.K.Mishra,and S.Misra,J.Plasma Phys.75(2009)731.
[45]N.A.Chaitanya,M.V.Jabir,J.Banerji,and G.K.Samanta,Sci.Report 6(2016)32464.
[46]S.Misra and S.K.Mishra,Prog.Electromagnetics Res.B 16(2009)291.
[47]R.M.Herman and T.A.Wiggins,J.Opt.Soc.Am.A 8(1991)932.
[48]X.Wang and M.G.Littman,Opt.Lett.1(1993)767.
[49]C.Paterson and R.Smith,Opt.Commun.124(1996)121.
[50]C.Zhao,Y.Cai,F.Wang,et al.,Opt.Lett.33(2008)1389.
[51]A.B.Borisov,A.V.Borovskiy,O.B.Shiryaev,et al.,Phys.Rev.A 45(1992)5830.
[52]H.S.Brandi,C.Manus,G.Mainfray,and T.Lehner,Phys.Rev.E 47(1993)3780.
[53]R.Gupta,P.Sharma,M.Rafat,and R.P.Sharma,Laser part.Beams 29(2011)227.
[54]P.Sharma,A.K.Bhardwaj,and R.P.Sharma,J.Phys.:Conf.Ser.534(2014)012049.
[55]P.Sharma,Laser Part.Beams 33(2015)755.
[56]J.T.Mendonca and J.Vieira,Phys.Plasmas 21(2014)033107.
[57]J.Vieira and J.T.Mendonca,Phys.Rev.Lett.112(2014)215001.
[58]A.S.Akhmanov,A.P.Sukhorukov,and R.V.Khokhlov,Sov.Phys.Usp.10(1968)609.
[59]M.S.Sodha,V.K.Tripathi,and A.K.Ghatak,Prog.Optics 13(1976)169.
[60]J.Krall,A.Ting,E.Esarey,and P.Sprangle,Phys.Rev.E 48(1993)2157.
 Communications in Theoretical Physics2018年1期
Communications in Theoretical Physics2018年1期
- Communications in Theoretical Physics的其它文章
- Solitary Potential in a Space Plasma Containing Dynamical Heavy Ions and Bi-Kappa Distributed Electrons of Two Distinct Temperatures
- Ti Impurity Effect on the Optical Coefficients in 2D Cu2Si:A DFT Study?
- Simultaneous Effects of Impurity and Electric Field on Entropy Behavior in Double Cone-Like Quantum Dot
- Discrete Boltzmann Method with Maxwell-Type Boundary Condition for Slip Flow?
- Unique Outcomes of Internal Heat Generation and Thermal Deposition on Viscous Dissipative Transport of Viscoplastic Fluid over a Riga-Plate
- Spatial Dependent Spontaneous Emission of an Atom in a Semi-In finite Waveguide of Rectangular Cross Section?
