Hojun Kim, Seyoung Kim, Yulong Shang, Seunghyeon Kim, Taejin Jung,＊

1 Department of Electronics and Computer Engineering, Chonnam National University, Gwangju 61186, Republic of Korea

2 R&D Planning and Management Team, Giga KOREA Foundation, Daejeon 34054, Republic of Korea.

I. INTRODUCTION

In broadcasting systems, a single frequency network (SFN) [1]–[2] offers many advantages including efficient utilization of the radio spectrum and also an increase in coverage over larger geographical areas. However, multiple transmitters in an SFN synchronously broadcast the same symbols at the same frequency band to diminish the shadowed area.The overlapped signals at a receiver side may therefore cancel each other out due to their opposite phases, leading to the possibility of an undesirable disappearance of the transmitted signals, which is referred to as an erasure event [3]–[6]. According to [6], the erasure event occurs up to 15% of the time in DVB-T2 systems.

To mitigate the erasure event, a number of schemes with higher diversity gains based on a constellation-rotation (CR) method have been introduced for SFN networks [6]–[10]. Of these, the scheme of [6] has been adopted as the specification of DVB broadcasting systems[4]–[5]. However, these CR schemes were originally invented for the broadcasting systems employing only a single transmit antenna, such as single-input single-output (SISO)and single-input multiple-output (SIMO).

Recently multiple-input multiple-output(MIMO) systems have continuously attracted interest due to the need for a high spectral-efficiency in next-generation broadcasting systems. Specifically, a so-called spatial-multiplexing (SM) scheme using two transmit and two receive antennas was adopted for the DVB next-generation hand-held system(DVB-NGH) [5]. However, when applying the SM to the SFN systems, some practical considerations apply since the multiple MIMO transmissions in the SFN deteriorates the signal quality due to an increase in erasure events, and thus the high spectral-efficiency in the SM may not be available any more in a real environments. Unfortunately, to the best of our knowledge, any research wherein the erasure effect is examined or mitigated regarding MIMO systems has not been presented.

Therefore, in this paper, we propose a new SM scheme for an orthogonal precoder employed in two transmit and two receive antennas. The precoder is optimized through an analytical minimization of the average bit error rates (BERs) for 4- and 16-QAMs over the erasure Rayleigh-fading channels. The optimized angles in the precoder are distinct from those of unitary precoders that have been used in conventional correlated MIMO channels [11] and space-time coded systems [12].These analytical results show that the performance of the ordinary SM is greatly degraded by the erasure effect in the FTN and also the optimized precoder in the new SM has a great role in compensating for the performance loss incurred by the erasure effect. Compared to the conventional CR scheme [6], the advantages of the proposed SM is great regarding the BER performance, especially for higher erasure-ratio values.

Meanwhile, the channel estimation is one of important issues for the coherent digital communications. In coherent MIMO systems,a widely-used channel estimation algorithm has been basically proceeded by inserting orthogonal pilot signals into each transmit antenna, and thus guaranteeing virtually perfect channel estimation at a receiver in the SFN channel environment [13-14].

The rest of this paper is organized as follows: in section II, we briefly review the conventional CR scheme for a single transmission antenna over the erasure fading channels; in section III, the precoded SM is presented with an optimalθover the erasure fading channels; and finally, the results of the simulation and the conclusions are presented in sections IV and V, respectively.

In this paper, we propose a new precoded SM scheme that achieves the diversity effect for erasure fading environments in SFN. The precoder in the proposed SM is optimized through the minimization of the average BER.

II. CONVENTIONAL CR SCHEME FOR SIMO SYSTEMS

The SFN is a broadcasting network comprised of several transmitters that simultaneously send an identical signal over the same frequency channel. Therefore the erasure event occasionally occurs in the SFN-channel model. As previously mentioned, the CR techniques [6]-[10] are much more effective over the erasure fading channel for the single-transmission antenna systems, such as SISO and SIMO.

Figure 1 depicts the conventional CR scheme [6] with single transmit and two receive antennas adopted in the DVB systems[4]-[5]. The detailed CR and cyclic-shifting(C/S) operations are shown infigure 2.

First, in the transmitter, thek-th input symbolxkis CR modulated by a rotation angleθ,Every imaginary component ofrkis cyclically shifted once to the right as shown infigure 2. Then the cyclic-shifting signals pass through the fading channels which are modeled asewhereis an erasure coefficient for thej-th receive antenna, andis a Rayleigh fading-channel gain that is modeled as an independent and identically distributed (i.i.d.) complex Gaussian random variable with a zero mean and an unit variance.

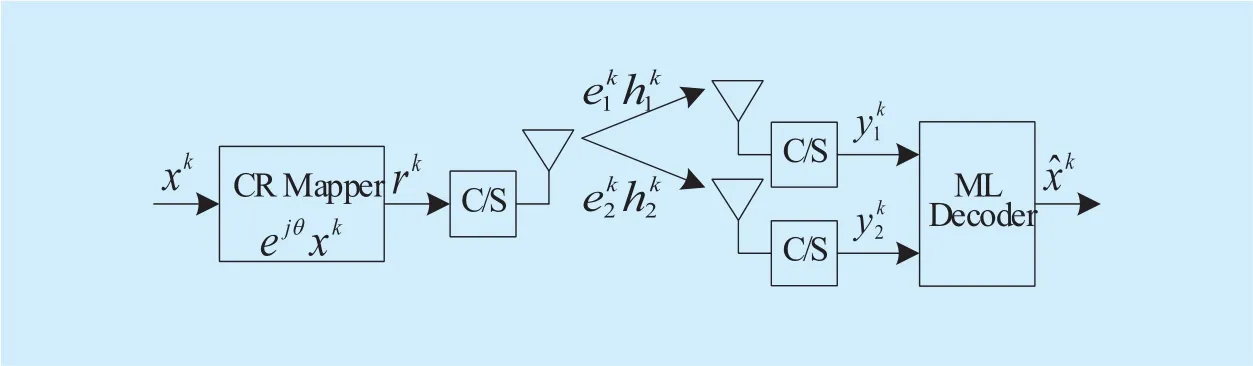
Fig. 1. Block diagram of conventional CR systems [6].

In realistic SFN environments, the values of the erasure coefficientmight be more complicated since the received signal is generated by overlapping multiple and identical signals with independent channel gains and phases.Thus [4]–[7], including DVB specifications,use a simplemodeling approach whereis an independent binary random variable with values of 0 with a probability ofPeand 1 with a probability of 1?Pe. Notably, the received signal must be normalized bywith the total-unit-received energy at the receiver serving as a constraint of the total received energy[6]–[7].

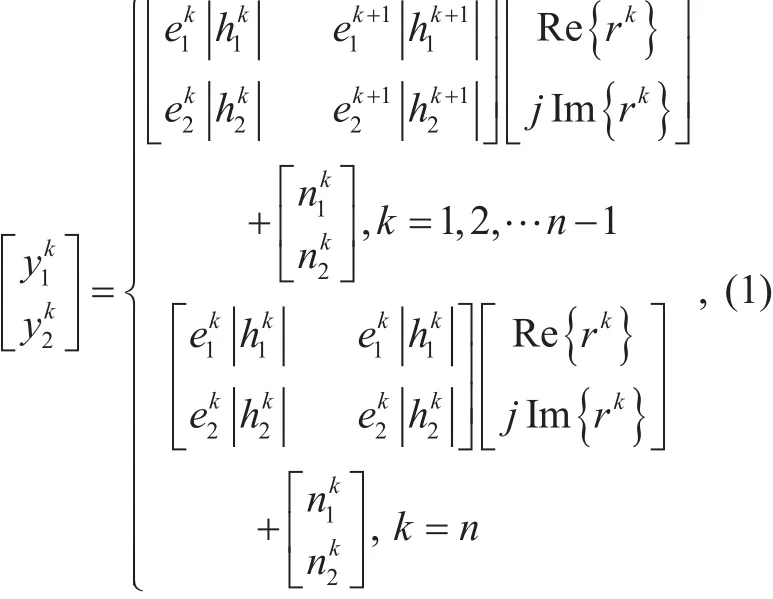
Fig. 2. Detailed CR and cyclic-shifting operations.

Fig. 3. Block diagram of proposed SM scheme.

After proceeding the reverse cyclic-shifting operation and then the channel-phase compensation work with perfect channel information at the receiver, thek-th received signalcorresponding torkcan be written as where Re{·} and Im{·} are the real and imaginary components of the signal, respectively, anddenotes an i.i.d. complex white Gaussian noise sample with a zero mean and a variance of 2σ2. The maximum-likelihood(ML) decoding for the received signal of (1) is therefore carried out as

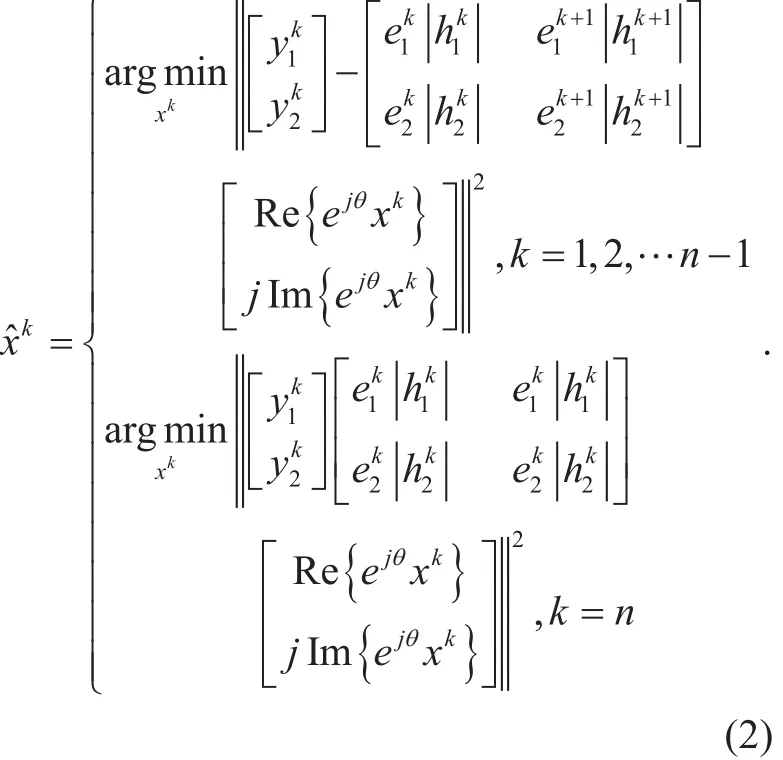
In [6], the finally transmitted CR signals infigure 2 are assumed to pass over the ideal independent erasure fading channel throughout the ideal symbol interleaving. Therefore each of the real and imaginary components of every rotated symbol are guaranteed to undergo independent erasure fading. Hence if at least one of the two components arrives without error at the receiver, the demodulator can recover the symbol perfectly, even with the erasure event.Consequently, throughout the CR method, the SIMO transmission scheme in figure 1 has an additional diversity gain of 2, resulting in total diversity gain of 4 including the receive antenna diversity gain of 2. The optimized CR angles for a variety of modulation types under the erasure Rayleigh-fading channels are shown in table 1 [6].

The conventional CR scheme was originally introduced solely for single-transmission antenna systems like SISO and SIMO. However, MIMO systems are specified as a SM scheme have been adopted for a variety of recent broadcasting standards such as DVBNGH [5] to offer high-quality broadcast services. Therefore, in the following section, we propose a new SM scheme that achieves the transmit diversity gain for the erasure MIMO environments like that of the conventional CR scheme in SISO or SIMO systems.

III. PROPOSED SM SCHEME FOR MIMO SYSTEMS

3.1 System model of the proposed scheme

Figure 3 depicts a block diagram of the proposed SM scheme which is basically constructed from the serial concatenation of an orthogonal precoder with the standard SM scheme. The MIMO channels are assumed to be i.i.d. Rayleigh-fading channels with erasure events.

Here,whereei,jandhi,jdenote an erasure coefficient and a Rayleigh-fading-channel gain, respectively,between thei-th transmit and thej-th receive antennas. Eachei,jis modeled as an independent binary random variable identical to that of figure 1. Also,denotes an additive white-Gaussian noise vector of a 2×1 size.Assuming a perfect knowledge of H at the receiver, the ML decoding can be expressed as the follows:

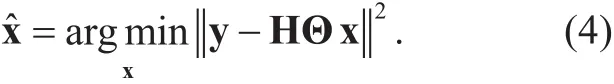
Table I. Optimized CR angles [6].

3.2 Optimization of the orthogonal precoder Θ

Notably, the proposed scheme of figure 3 is simply reduced to the ordinary SM scheme if the angleθused in Θ is set to be zero since Θ=I2. Here, I2is the identity matrix with a 2×2 size. By varying the value ofθ, we examine the performance of the standard SM over the erasure fading channels. Furthermore,if an optimum non-zero value ofθexists, a new SM scheme that copes with the serious erasure effect can be found.

If the two received antennas are symmetric and independent,θis optimized over any given receive antenna to minimize the overall error performance. To simplify the optimization ofθ, we will therefore only considery1for the signal detection at the receiver, and this can be written as

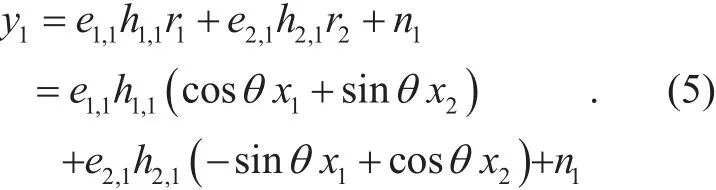
From (5), we can classify all possible erasure events into four specific cases with respect to the values ofe1,1ande2,1.Thus with a givenpe, the average BER,P(E) can be written as

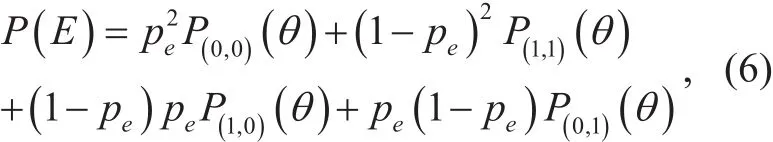
whereP(a,b)(θ) denotes the conditional average BER forWe will subsequently proceed with the optimization work by separately minimizing eachP(a,b)(θ) overθ.

In this case, we can see from (5) that only the noise component is contained in the receive signalmeaning that absolutely no connection exists between the angleθand the conditional BERP(0,0)(θ)(orP(E)). Intuitively, it is obvious that if all of the signals disappear as in this worst-case scenario due to the erasure events, there are no methods to compensate for the erasure effect at the receiver.

This case is identical to the conventional non-erasure fading channels, whereby (5) is simpli fi ed as follows:

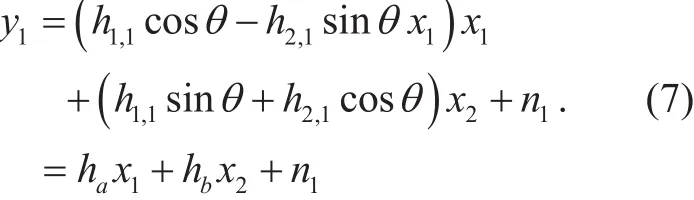
According to (7), the i.i.d. Rayleigh distributions of the effective channel gainshaandhbare identical to those ofhi,jin (3) due to the orthogonality of Θ for any values ofθ.This means thatθdoes not affectP(1,1)(θ) (orP(E)) in the same way thatP(0,0)(θ) for case A is affected.

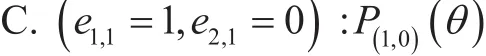
In this case, only one of the signals transmitted from the first antenna survives as the receiver, so (5) can be rewritten as follows:

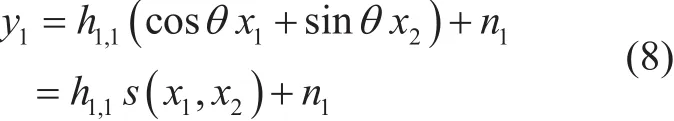
From (8), we see that this is identical to the case in which the new signalis transmitted over a single Rayleigh fading channel in SISO systems. Therefore,P(1,0)(θ)can be calculated by using the traditional analysis for SISO systems [15]-[16]. In this paper,we consider two modulation types of 4- and 16-QAMs for the modulated signalxi.

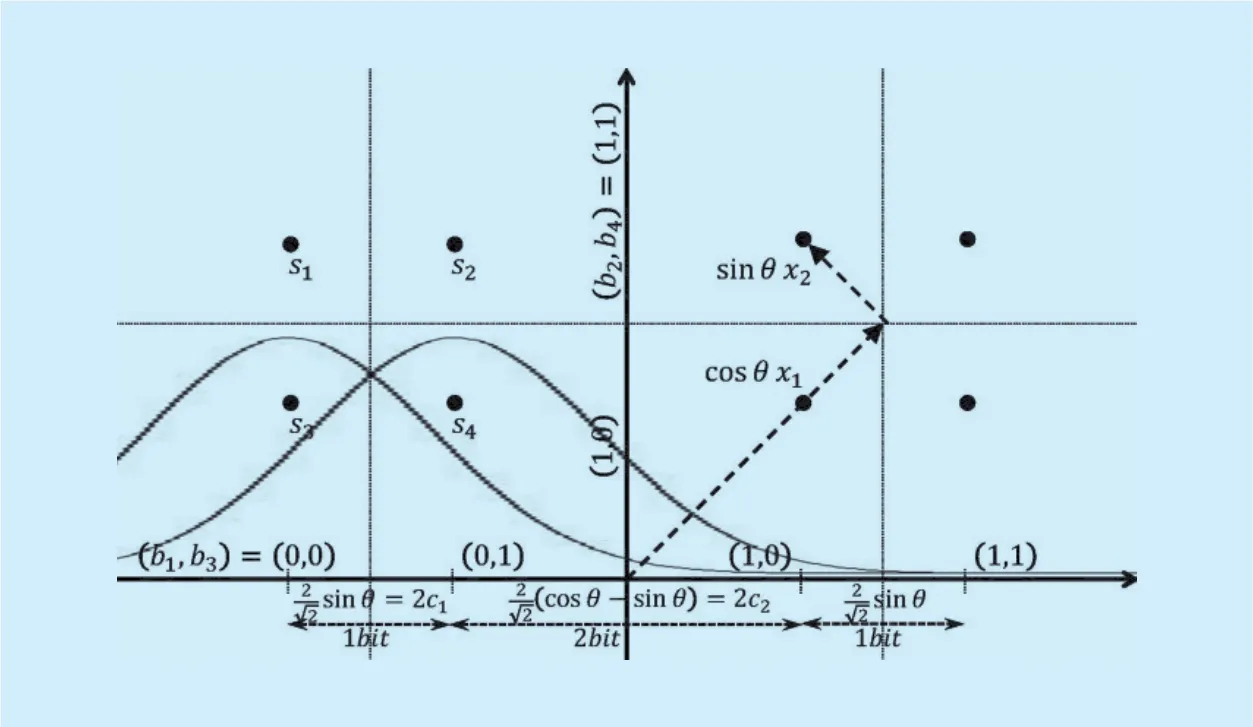
Fig. 4. Constellation of for 4-QAM.

Figure 4 illustrates the precoded symbol constellation,with a givenθ, wherex1andx2are gray-mapped 4-QAM symbols corresponding to bit pairsandrespectively. Due to the symmetry ofoverθ, we assumeθin

It should be noted that, althoughconsists of the two gray-mapped 4-QAM sym-is no longer gray-mappedas shown in figure 4.Therefore, the routine optimization approach that is based on the maximization of the minimum Euclidean distance between any two constellation points no longer holds in this case.

Assuming equally likely transmit symbols,we will first calculateconditioned

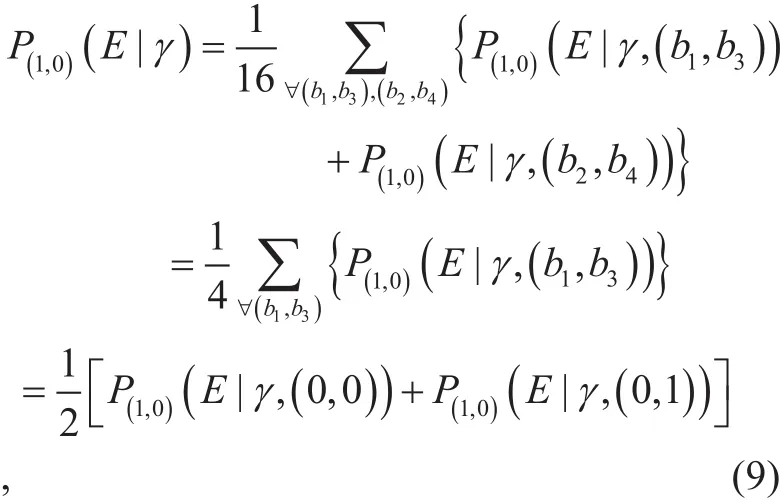
wheredenotes the conditional BER of the 4-QAM whenThe equality of (9) uses the symmetry of the 4-QAM constellation for its in-phase component, as can be seen infigure 4. Then, after various manipulations, the two conditional BERs of (9) can be calculated in terms of the GaussianQ-function,Q(·) as follows:

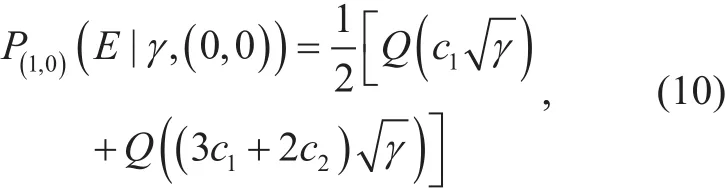
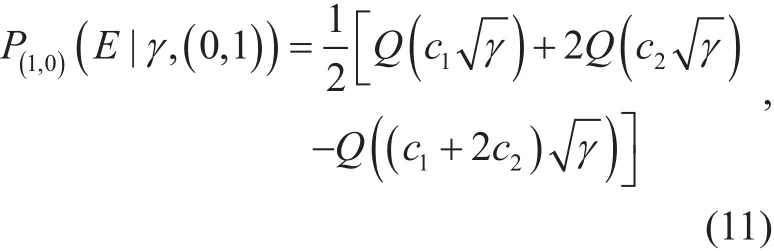
whereBy putting (10) and(11) into (9) and then averaging (9) overγ,we can finally derivefrom the following:

From figure 5, we can observe that the original SM, i.e.,θ=0o, is no longer optimal when the erasure event occurs in this case C, unlike the non-erasure case B. Intuitively,to perfectly recoverx1andx2in (8) in the absence of noise, the further absence of ambiguity inoverx1andx2, implying a non-zero optimumθvalue, is essential.Namely the precoder Θ with a non-zeroθguarantees that each of the information signalsx1andx2are simultaneously passed through both transmit antennas. Hence, if at least one path survives at the receiver, as described in(8), all signals can be perfectly recovered in the absence of noise, causing a transmit antenna diversity gain of two.

To determine an optimumθvalue in figure 5, we assumeat high SNRs, thereby simplifying (12) into

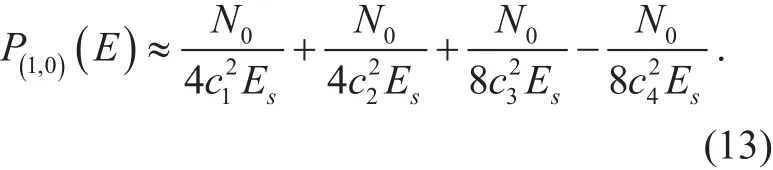
By calculatingmerically obtain the optimum angleθfor 4-QAM:

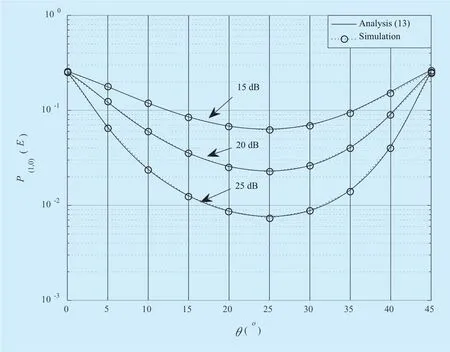
Fig. 5. Performance of versus θ for 4-QAM.

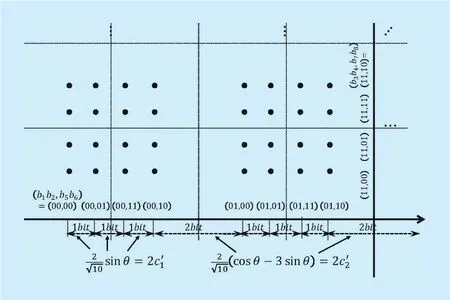
Fig. 6. Constellation of for 16-QAM.

Figure 6 illustrates the constellationwhen the gray-mapped 16-QAM symbolsx1andx2that correspond torespectively,are used. It is worth noting thatfigure 6 is also not gray-mapped, as in the case of 4-QAM infigure 4. Thus using an equally likely transmission of symbols and the symmetry of the 16-QAM constellation, the BERconditioned onγcan be calculated as follows:

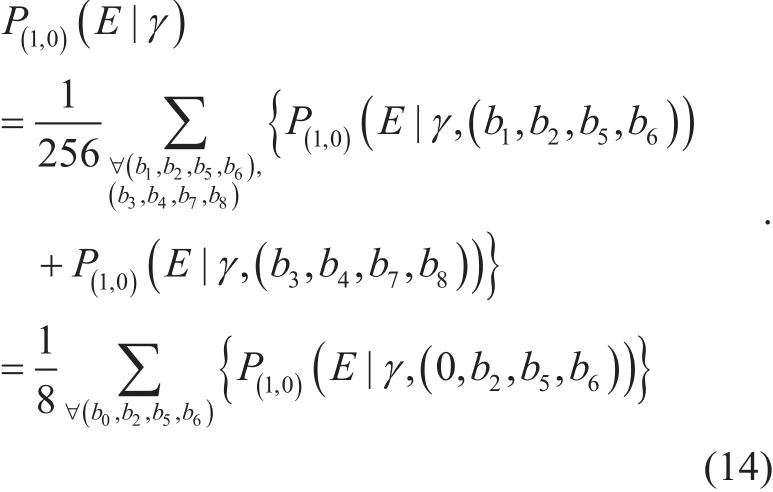
The directcal culations ofin (14) are more complicated unlike (9) regarding 4-QAM.Hence by only taking the adjacent bit decision boundary into account to calculatefor a high SNR value, we approximately derive

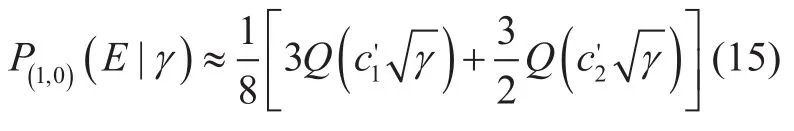
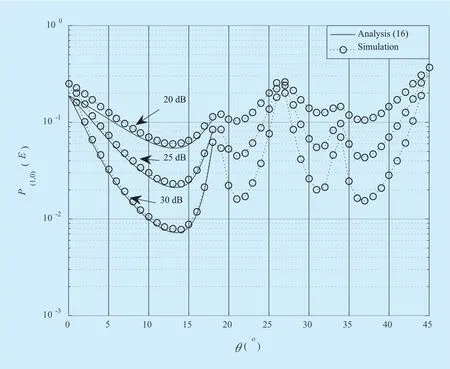
Fig. 7. Performance of ) versus θ for 16-QAM.

whereThen by averaging(15) overγ, we finally derive an approximat-as follows:

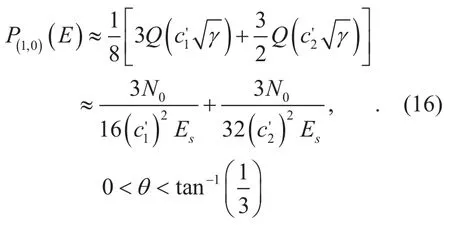
The results of the analysis in from (16) are shown infigure 7 and appear to fit well with the results of the simulation. According to figure 7, the performance trends are similar to those of 4-QAM for identical reasons. Finally, by differentiatingwith respect toθ, we numerically obtain an optimum value ofθfor 16-QAM, as follows:

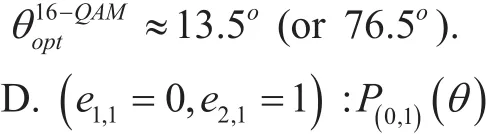
Here, this case is identical to the previous case C in the sense that only one signal path survives at a receiver. Therefore, due to the symmetrical performance with respect toθ,the optimumθs for 4-QAM and 16-QAM will be identical to those optimized in the case C ofP(1,0)(θ).

In this way, an optimum rotation angle can be obtained for 4QAM and 16QAM that are different from the conventional CR scheme in table 1.

IV. SIMULATION RESULTS

In this section, we will compare the results of the simulation of the proposed SM with the optimum valueθoptand the standard SM (or the proposed SM withθ=0). The results of the performance of the conventional CR scheme [6] are also included for both cases of one (SISO) and two (SIMO) receive antennas.For the proposed scheme, the optimum anglesθoptof 25.2ofor 4-QAM and 13.5ofor 16-QAM are used, as is the case before induction.All of the schemes are simulated under the i.i.d. Rayleigh channel model withpe=0%(non-erasure) and 15% at maximum [6]–[7].

4.1 Non-erasure fading channels(pe=0%)

Figure 8(a) shows the average BERs for the 4-QAM over the ordinary non-erasure fading channel. To send the same total-information bits at each symbol time, the CR with one transmit antenna uses 16-QAM. At first, we see that the results of the proposed SM are identical with those of the ordinary SM. This is obvious since the orthogonal precoder Θ does not affect the performance for the non-erasure channels due to the corresponding orthogonality irrespective ofθ. Namely,if the erasure event is nonexistent in an SFN network, any additional performance gain regarding the proposed SM does not eventuate,even though the precoder at the transmitter is utilized. This result was previously described in case B ofP(1,1)(θ).

Next, the performances of the proposed SM are more effective than those of the conventional SISO-CR under all SNR regions. However, the performances of the conventional SIMO-CR are better than those of the proposed SM under the high SNR regions. This fi nding is due to the much higher diversity gain of 4 of the conventional SIMO-CR that is inherent to the CR diversity of 2 and the receive-antenna diversity of 2. Meanwhile, the receive-antenna diversity gain of the proposed SM is only two.

Figure 8(b) shows the average BERs for 16-QAM. Here, 256-QAM is used in the CR scheme for a total of 8 bits can be transmitted. infigure 8(b), the performance trends of the proposed SM, the conventional SM, and the SISO-CR are clearly the same as those of figure 8(a). However, for the SIMO-CR,its performance is far poorer than that of the proposed SM, even for high SNRs of interest.Obviously, the diversity gain of the SIMO-CR is larger than that of the proposed SM, like the 4-QAM of figure 8(a). However, the performance loss is incurred from the use of a relatively much- higher modulation order in the SIMO-CR that is dominant in this case.

Fig. 8. Average BERs over pe=0%.

4.2 Erasure fading channels(pe=15%)

Fig. 9. Average BERs over pe=15%.

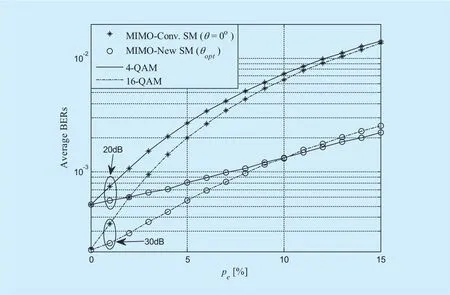
Fig. 10. Average BERs versus pe.

Figure 9(a) shows the average BERs for the identical schemes in figure 8(a) overpe=15%. First of all, the proposed SM is shown to outperform the conventional SM because, for the erasure channels, the optimum precoder guarantees non-ambiguity in the signal constellations at the receiver, causing an additional diversity effect over an erasure event, unlike the non-erasure cases of Figs. 8 and 9. An easily formulated conjecture here is that the much larger performance gap will happen regarding a higherpevalue. Next the performance of the new SM is more favorable than those of the CR schemes for all SNR values. Notably, unlike of Figs. 8 and 9, the proposed SM has a diversity gain of 4 identical to that of the SIMO-CR since the new SM enjoys the additional diversity gain of 2 based on the precoder for the erasure channels. Therefore the lower modulation order used in the proposed SM will be dominant, resulting in a relatively better BER performance.

Finally, we notice in figure 9(a) that asincreases, the BERs for all schemes converge, meaning that even in the absence of noise, bit-detection errors take place at the receiver with a non-zero probability. This phenomenon is obvious since, for the erasure events with a non-zerope, the disappearance of the transmitted signals will absolutely occur at the receiver. Thus, the information bits have to be randomly determined at the demodulator. Specifically, the proposed SM and the SIMO-CR schemes achieving a diversity order of 4 convey the information signals through four independent erasure-channel paths with each an identicalpe. Hence the signal disappearance takes place at the receiver with a probability ofpe4, resulting in a randomly decided BER ofpe=15%, the BERs for these schemes con-as observed in figure 9(a). Obviously, the conventional SM and SISO-CR schemes with a total diversity order of 2 will converge to a BER value of, as shown in figure 9(a).From these results, we conclude that, for SFN networks, it is great essential to employ the diversity techniques to cope with the erasure events, such as the precoding method in the proposed SM or the CR method [6].

Figure 9(b) shows the average BERs for the identical schemes in figure 8(b) overpe=15%. All BER curves show similar trends to those of figure 9(a). At first, the proposed SM is the most favorable among all schemes due to the same reasons in those of figure 9(a).The BER-convergence phenomenon for high SNRs is also observed with the identical BER values infigure 9(a) because the probability of signal disappearance for the erasure channels is only dependent on the inherent diversity order andpe, and it is not relevant to the modulation type.

Figure 10 shows the plots of the average BER for the erasure-ratiopevalues from 0%to 15%. These results indicate that the sensitivity of the proposed scheme is much lower with respect topethan that of the ordinary SM scheme. This is mainly due to the fact that the much higher diversity effect in the proposed SM is dominant as increasingpe. The proposed scheme is therefore one of the most effective and practical solutions for the mitigation of the erasure effect in the SFN networks.

V. CONCLUSIONS

In this paper, we propose a new precoded SM scheme that achieves the diversity effect for erasure fading environments in SFN. The precoder in the proposed SM is optimized through the minimization of the average BER. The performance improvement of the proposed SM is greater regarding higher erasure ratios and SNRs, without any loss of performance in the non-erasure fading channels. In addition,the performance of the new SM scheme is more effective than that of the conventional CR scheme over the erasure fading channels.

References

[1] R. Rebhan and J. Zander, “On the Outage Probability in Single Frequency Networks for Digital Broadcasting,”IEEE Transactions on Broadcasting, vol. 39, no. 4, 1993, pp. 395–401.

[2] A. Mattsson, “Single Frequency Networks in DTV,”IEEE Transactions on Broadcasting, vol. 51,no. 4, 2005, pp. 413–422.

[3] B. T. Irons and K. D. Donohue, “Probability of Erasure in Non-Rayleigh Fading Channels—A Simulation Study,”IEEE Transactions on Communications, vol. 43, no. 2, 1995, pp. 1246–1247.

[4] ETSI EN 302 755 v.1.3.1, Digital Video Broadcasting (DVB); Framing Structure, Channel Coding and Modulation for a Second Generation Digital Terrestrial Television Broadcasting System (DVB-T2), Apr. 2012.

[5] ETSI EN 303 105 v.1.1.1, Digital Video Broadcasting (DVB); Next Generation Broadcasting System to Handheld, Physical Layer Specification (DVB-NGH), Nov. 2012.

[6] C. A. Nour and C. Douillard, “Rotated QAM Constellation to Improve BICM Performance for DVB-T2,”Proc. IEEE 10th International Symposium on Spread Spectrum Techniques and Applications, 2008, pp. 354-359.

[7] C. A. Nour and C. Douillard, “Improving BICM Performance of QAM Constellations for Broadcasting Applications,”Proc. 5th International Symposium on Turbo Codes and Related Topics,2008, pp. 44-60.

[8] L. Sun, T. Zhang, L. Lu, and H. Niu, “Spectrally-Efficient Decode-and-Forward Scheme Based on Constellation Rotation,”ETRI Journal, vol. 32,no. 4, 2010, pp. 607-609.

[9] T. J. Jung, H. S. Lim, “Design of a New 4-Dimensional Constellation-Rotation Modulation Method for DVB-NGH,”IEICE Transactions on Communications, vol. E95.B, no. 11, 2012, pp.3625-3628.

[10] D. Gozalvez, J. J. Gimenez, D.Gomez and N.Cardona, “Rotated Constellations for Improved Time and Frequency Diversity in DVB-NGH,”IEEE Transactions on Broadcasting, vol. 59, no. 2,2013, pp. 298-305.

[11] J. Akhtar and D. Gesbert, “Spatial Multiplexing over Correlated MIMO Channels with a Closed-Form Precoder,”IEEE Transactions on Wireless Communications, vol. 4, no. 5, 2005, pp. 2400-2409.

[12] Y. Xin, Z. Wang, and G. B. Giannakis, “Space-Time Diversity Systems Based on Linear Constellation Precoding,”IEEE Transactions on Wireless Communications, vol. 2, no. 2, 2003, pp.294-309.

[13] Z. Zhang, J. Liu, and and K. Long, “Optimal Pilots Design for Frequency Offsets and Channel Estimation in OFDM Modulated Single Frequency Networks”,Proc. IEEE 7th International Conference on Wireless and Mobile Computing,Networking and Communications, 2011, pp.411-415.

[14] Y. Li, X. Xu, D. Zhang, Z. Zhang, and K. Long,“Optimal Pilots Design for Frequency Offsets and Channel Estimation in OFDM Modulated Single Frequency Networks”,Science China Information Sciences, vol. 57, no. 4, 2014, pp.1-12.

[15] M. K. Simon, ed.,Digital Communication over Fading Channels, NJ, 2004.

[16] M. S. Alouini and A. Goldsmith, “A uni fi ed approach for calculating error rates of linearly modulated signals over generalized fading channels,”IEEE Transactions on Communications,vol. 47, no. 9, 1999, pp. 1324-1334.