Xu-Dong Zheng·Qi Wang

1 Introduction

In the context of bipedal walking,passive dynamic walking is a walking method for which the walker moves down an incline under the effect of gravity without an exogenous source of energy.The concept of planar passive dynamic walking was first introduced by McGeer [1], who built a classof prototypes. Passive dynamic walking is expected to significantly improve the energy efficiency of bipedal locomotion[2].The concept has also been investigated to obtain additional insight into the design principles of legged locomotion in nature[3].

A great number of studies have been conducted both experimentally and theoretically since the introduction of the concept of passive dynamic walking.Excellent studies have originated from the laboratories of Cornell,Delft,and M IT[4–6].The gait of a straight leg model was systematically studied by Liu et al.[7,8]via simulations and experiments,while Gritli and Belghith[9–12]analyzed the walking dynamics of a passive compass-gait model under OGY-based control,and provided a numerical calculation method for the spectrum of Lyapunov exponents based on a controlled hybrid Poincaré map.However,all the above mentioned studies were based on McGeer’s assumptions:(1)there is no slip between the foot of the stance leg and the floor;(2)the impact between the foot of the swing leg and the floor is modeled as fully inelastic and instantaneous;(3)an exchange between the stance and swing legs occurs at the time of impact[1].

In contrast to the previous studies,Qi et al.[13,14]discussed the contact stiffness,contact damping,and coefficients of friction between the feet and the ground,and verified their study through both experiments and numerical simulations.They found that if the friction was small enough,the feet might slip on the ground.In other works,Asano et al.[15–18]proposed a locomotion robot that slides and rotates on a slippery downhill, and demonstrated that a stable passive compass gait could be generated,but they ignored the inertia moment of the leg frame.It must be pointed out that both Qi’s and Asano’s studies were based on the modified Coulomb friction law,which lacks the characteristics of static friction[19].Moreover,they did not consider the bouncing of the stance leg in the gaits of passive walking.Similarly,Gamus and Or[20]investigated simple and low-dimensional models of dynamic bipedal walking under possible foot slippage using constrained Lagrange equations.They did not distinguish between static and dynamic friction.In addition,they did not investigate the bouncing of the stance leg.

Mechanical systems such as slider-crank mechanisms with revolute clearance joints and passive dynamic walkers constitute multibody systems with unilateral contacts and friction,whose dynamic equations are non-smooth[21].The theory of non-smooth multibody system dynamics can be used to investigate the dynamical behavior of these mechanical systems[22–25].The main difficulty in solving non-smooth dynamic equations of multibody systems with friction results from instantaneous changes in the frictional forces at the transition from sliding to sticking or reverse sliding.Fortunately,the stick-slip transition between two contacting bodies with friction can be formulated as a linear complementarity problem(LCP)and solved[26–28].For example,Duan et al.[29]used the LCP method to establish the dynamic model of a passive dynamic walker,and found a stable periodic gait with a stick-slip phenomenon between the stance leg and the floor.However,the authors used a time-stepping scheme to solve the dynamic equations of the walker,and it was necessary to assume that the coefficients of kinetic and static friction were equal.

The purpose of this paper is to present an LCP method for a planar passive dynamic walker with round feet based on an event-driven scheme.The remainder of the paper is organized as follows:Sect.2 presents the modeling and dynamic equations of the passive dynamic walker.The contact force models utilized in the present work are also briefly introduced.In Sect.3,using an event-driven scheme,the problem of the stick-slip transitions of the feet and floor is formulated as an LCP and is solved.Methods for preventing the swing leg from scratching the floor are also described.In Sect.4,numerical examples are illustrated to demonstrate the four gaits of the walker.Finally,the main conclusions of the study are presented in the last section.

2 Modeling and dynamic equations o f the passive dynamic walker

2.1 Modeling of the passive dynamicwalker

Consider a planar model of a passive dynamic walker on an inclined floor[7].As shown in Fig.1,the model consists of a pair of rigid legs with round feet,which are labeled leg 1 and leg 2,interconnected through a perfect jointH.The mass centers of the two legs areC1andC2,respectively.For simplicity,the model is set as symmetrical,and each leg has a mass ofm,a length ofl,and a moment of inertia ofJabout mass centerCi(i=1,2),including the corresponding foot.Each foot is a part of circle and has a radius ofr,and the centers of the circles areO1andO2,respectively.The distance between the mass center of each leg and the hip isd,namely:

Fig.1 The model of the passive dynamic walker

The global parameters include the gravitational accelerationgand the slope angleα.For convenience of analysis,an inertial frame of referenceOxyis fixed on the inclined floor,in which thex-axis is parallel to the floor,while they-axis is perpendicular to the floor.Suppose thatxandyare the coordinates of the hipH,andθiis the counterclockwise angle between the negativey-axis and legi(i=1,2).The four generalized coordinates of the passive dynamic walker can be written as

2.2 Normal contact law

When the feet come in contact with the floor,small penetrations will occur near the contact are as,as shown in Fig.2.The best-known normal contact force law between two spheres of isotropic materials is the result of Hertz’s work,which is based on the theory of elasticity[30].Hertz’s law relates the contact force with a nonlinear power function of penetration depth and is written as

whereFNis the contact force,δrepresents the penetration depth between the contacting bodies,andKandnare the contact stiffness parameter and the nonlinear power exponent determined by the material and geometric properties of the local region of the contacting objects.

Hertz contact theory is restricted to frictionless surfaces and perfectly elastic solids,and the energy dissipation during the contact process is not taken into account.Many normal contact force models have been developed to describe the possible energy dissipation[31–33].One such model is used in our paper[32]:

Fig.2 The contact model of the walker feet with small penetrations

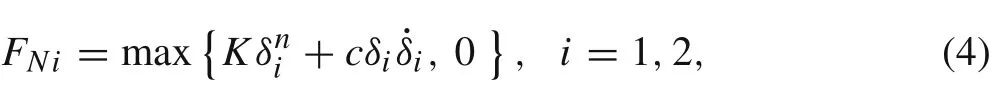
whereFNirepresents the normal contact force of footi.δiandare the penetration depth and velocity between footiand the floor,respectively.Kandcare the generalized stiffness parameter and the hysteresis factor,which are dependent on the radii of the feet and the material properties of the feet and floor.The exponentnis equal to 1.5 for the case where there is a parabolic distribution of contact stresses[30].For materials such as glass or polymer,the value of the exponentncan be either higher or lower[34].

By using geometrical parameters and generalized coordinates of the passive dynamic walker,the penetration depth between footiand the floor,δi,can be obtained,as illustrated in Fig.2

whereδi＞0 means that footicontacts or touches the floor,whileδi=0 means that footidoes not touch the floor.This meaning will be used in Sect.3.3.

2.3 Tangential contact law

Coulomb’s dry friction law is a fundamental and simple model of friction between dry contacting surfaces,and is frequently used to describe the friction phenomenon for contact problems.It can describe the characteristics of dry friction and illustrate the stick-slip phenomenon between contacting bodies,and its coefficients can be gained experimentally or by consulting handbooks on friction.Therefore,Coulomb’s dry friction model was adopted as the tangential contact law of the feet and the floor in this paper.

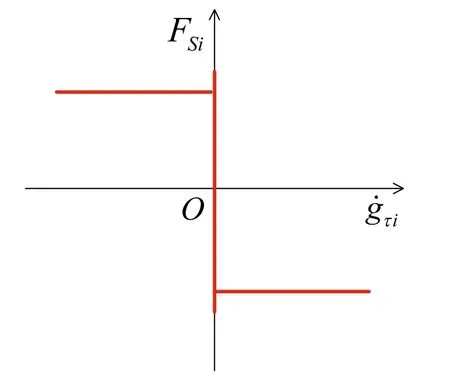
Fig.3 The Coulomb dry friction model

Coulomb’s dry friction law is given by

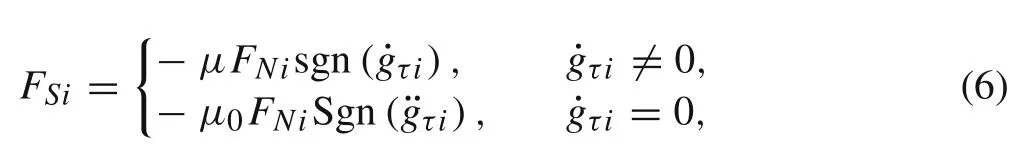
whereFSiis the frictional force acting on footi[35,36].is the tangential velocity of the contact point of footi,andare the coefficients of kinetic and static friction,respectively.μis generally smaller thanμ0.sgn(x)is the sign function,which is defined as

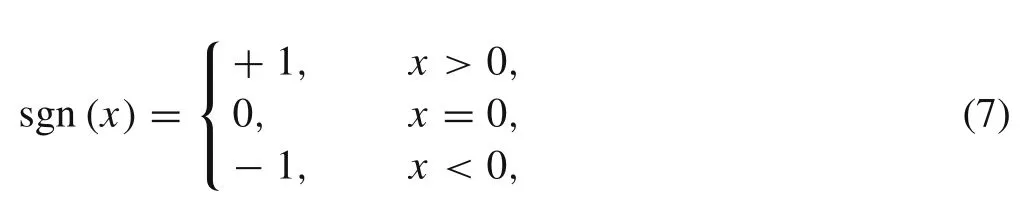
while Sgn(x)is the multivalued function,which is defined by[37],

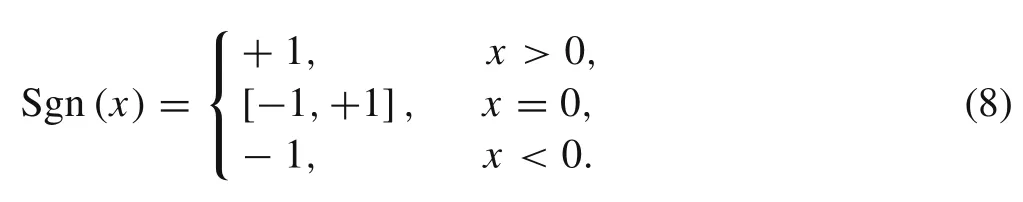
The Coulomb dry friction model is illustrated in Fig.3.

2.4 Dynamic equations

As a multibody system,the dynamic equations of the passive dynamic walker can be given by the Lagrange equations of the second kind:

The kinetic energy of the passive dynamic walker can be written as

whereis the positive definite mass matrix

3 LCP formulation based on an event-d riven scheme

Equations(6)and(18)will be used to describe the dynamical behaviors of the passive dynamic walker in numerical simulations.When the two feet of the walker are slipping on the floor or not touching the floor,i.e.neither is subjected to static frictions,the kinetic frictional forces acting on the feet can be written as

After inserting the above equation,Eq.(18)can be solved via a numerical method for ordinary differential equations(ODE).However,when one or both of the feet are sticking on the floor,the LCP scheme will be used to determine the static frictional forces and the stick-slip transitions of the feet in this paper.

3.1 Complementarities between friction saturations and accelerations

To solve the dynamic equations(18)numerically,the frictional forces acting on the feet of the passive dynamic walker must be determined.When˙gτi/=0,the footiis sliding,so its frictional force is given by the first equation of Eq.(6).When,the following three cases are possible:

When,it is difficult to determine the stick-slip transitions and the static frictional forces between the feet and floor.Based on the non-smooth dynamics approach[21],this problem can be transformed as an LCP and solved.

An LCP is a set of linear equations that can be written as

for which the vectoruandvmust be evaluated for givenAandb[38].In other words,the LCP involves finding solutionsuandvof Eq.(19)and conditions(20),whereb,u,andvaren-dimensional vectors,andAis ann-dimensional square matrix.

Whenis split into the positive and negative parts,which are defined as[39]

Consequently,the friction saturationsandare complementary to accelerationsand,respectively.The complementarity conditions can be expressed as

The equations above will be used in the next subsection.

3.2 Calculating the frictional forces in different situations

The tangential velocity of the(potential)contact point of footi,i.e.thexcomponent of the(potential)contact point velocity of footi,can be expressed as

The LCP forms are different according to the different contact situations of the passive dynamic walker and the floor.There are three contact situations:

Situation A:Stick state of stance leg 1

In this situation,leg1 is the stance leg with out slipping,which results in,while leg2 is either the swing leg or the stance leg with slipping,which results inFN2=0,orFN2＞0 withFor foot 1,Eq.(29)can be rewritten as

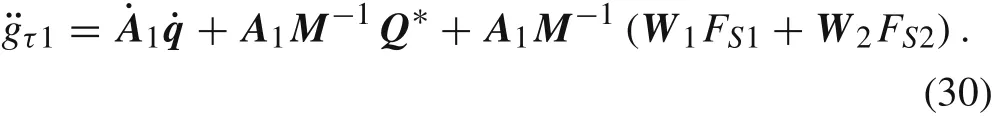
Combining Eq.(30)with Eq.(24)results in

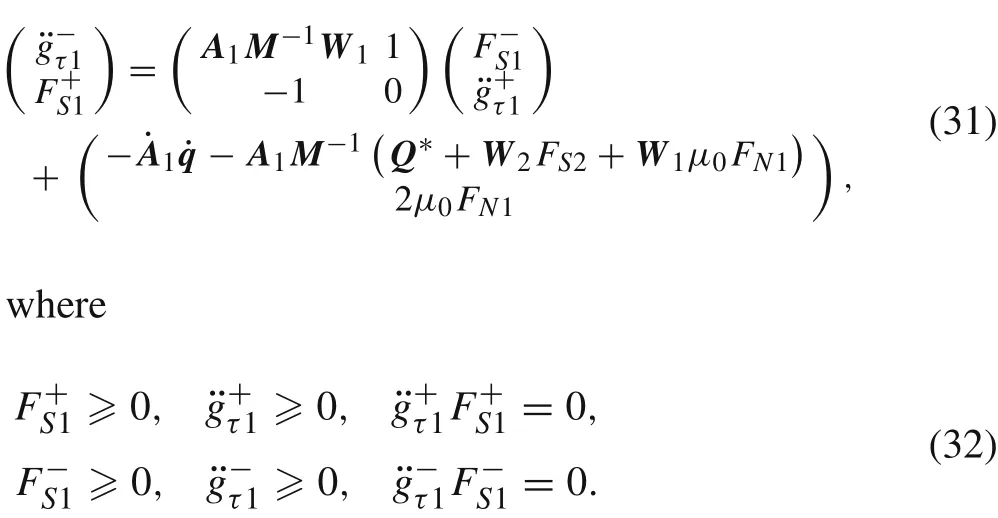
Using the LCP method,Eqs.(31)and(32)can be solved to determine the static frictional force and the stick-slip transition of foot 1.

Situation B:Stick state of stance leg 2

In this situation,leg2 is the stance leg without slipping,which results in,while leg1 is either the swing leg or the stance leg with slipping,which results inFN1=0,or.Then,For foot 2,Eq.(29)can be rewritten as

Using the LCP method,Eq.(34)and conditions(35)can be solved to determine the static frictional force and the stick-slip transition of foot 2.

Situation C:Stick state of two legs

In this situation,two legs stand on the floor without slipping,which meansFNi＞0 with˙gτi=0(i=1,2).Then,Eq.(29)can be rewritten as

Using the LCP method,Eq.(39)and conditions(40)can be solved to determine the static frictional forces and the stickslip transitions of the two feet.

Numerical methods for the LCP such as Lemke’s algorithm can be used to solve Eqs.(31),(34),and(39),along with the corresponding conditions to obtain the solutionSubstitutinginto the second equation of Eq.(24),the static frictional forceFSican be determined,and the dynamic equation(18)can then be solved by the numerical method for ODE.

3.3 Methods for preventing the swing leg from scratching the floor

When the stance leg is in contact with the floor,theswing leg may scratch the floor as it swings forward,affecting the normal walking of the passive dynamic walker.In experiments,Liu et al.[7]built a passive dynamic walker and a special floor in order to prevent the swing leg from scratching the floor,as shown in Fig.4.

Fig.4 The straight leg passive dynamic walker with round feet[7]

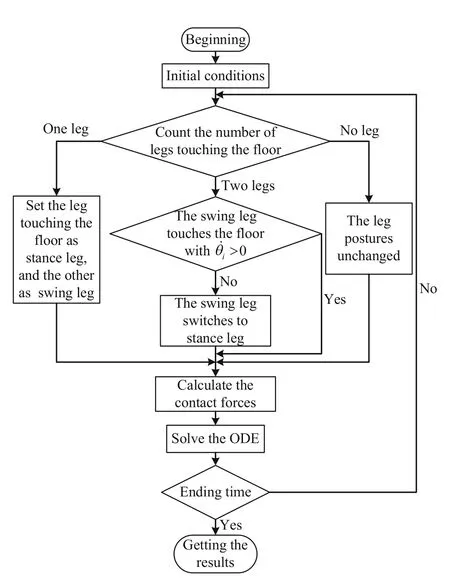
Fig.5 Simulation flow chart

In numerical simulations,we assume that a swing leg is not subjected to the contact forces to avoid scratching the floor.To determine whether legiis a stance leg or swing leg,several possible cases are given,as illustrated in the simulation flow chart of Fig.5.In order to realize walking,the initial conditions in Sect.4 are specially set to guarantee that only one leg touches the floor.

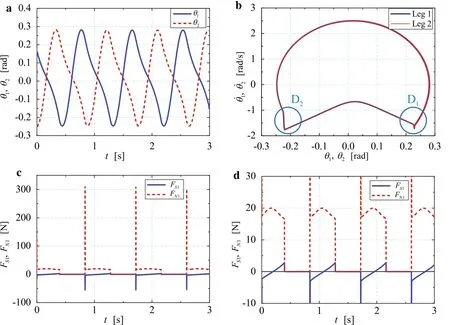
Fig.6 Simulation results of Gait I.a Time histories of swing angles;b Phase diagrams of θi and(i=1,2);c Time histories of contact forces acting on foot 1;d Magnified view of Fig.6c

4 Numerical examples

The parameters of the passive dynamic walker are set as:m=1.0 kg,J=0.0096 kg·m2,l=0.40 m,d=0.10 m,r=0.08 m[13].The gravitational acceleration:g=9.8 m/s2.The exponent of the modified Hertz contact law is set as:n=1.5.When˙gτi≤ε=1×10?5m/s,the contact point of footiis treated as zero.

4.1 Gait I:Stable periodic gait without bouncing and slipping of the stance leg

In the studies by Qi[13,14],the authors found a stable periodic gait of the passive dynamic walker in which the stance leg neither bounces nor slips,and verified their results by experiments.In order to verify the rationality of the contact models and the feasibility of the algorithms in this paper,the parameters and initial conditions from Ref.[13]are used in the simulation,and the simulation results are compared with theirs.The parameters and initial conditions are as follows:

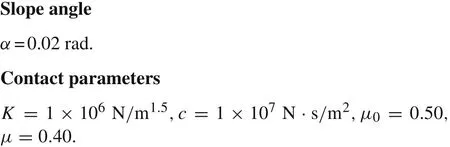
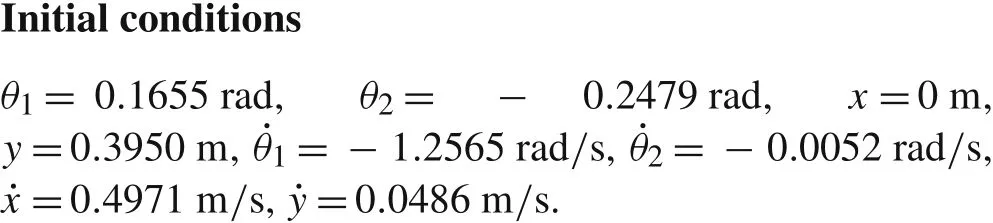
Figure 6a illustrates the time histories of the swing angles of the two legs,which are consistent with the literature results[13].The simulation results show that the motions of the two legs have the same stride and period.Figure 6b provides the phase diagrams ofθiand(i=1,2),which show that the passive dynamic walker enters a stable periodic gait at the very beginning.The region D1in Fig.6b illustrates that when hitting the floor,the swing leg is changed into a stance leg,and its angular velocity changes rapidly.In contrast contrary,the region D2in Fig.6b illustrates the moment when a stance leg switches to a swing leg.

Figure 6c depicts the time histories of contact forces acting on foot 1,and Fig.6d is a magnified view of Fig.6c.These calculation results show that foot 1 is subjected to a large impact both in normal and tangential directions when it hits the floor,and the direction of the friction changes during each step when leg 1 acts as a stance leg[22].The contact forces acting on foot 2 are identical to those of foot 1 except for a certain phase difference,so they are not given here.

Fig.7 Simulation results of Gait II.a Phase diagrams of θ1 and;b Phase diagrams of θ2 and;c Time histories of swing angles;d Tangential velocity of the(potential)contact point of foot 2 and its contact forces

4.2 Gait II:Stable periodic gait with slipping of stance leg

When the frictional coefficients between the feet and floor are small,the stance leg may slip on the floor.Various papers have dealt with this phenomenon[13,17,20,29].By choosing the parameters and initial conditions as follows,the gait in which the stance leg slips without bouncing is simulated in this paper.

Figure7a,b illustrates the phase diagrams of swing angles of the two legs.In order to show that the gaits are stable,the initial conditions are set intentionally away from the limit cycle.The time histories of the swing angles are given in Fig.7c.These simulation results show that the walker moves with a stable periodic gait after adapting several steps,and the motions of the two legs have different strides.Figure 7d depicts the time histories of the contact forces acting on foot2 and the tangential velocity of the(potential)contact point of foot 2.Region D in Fig.7b and region E in Fig.7d show that leg 2 slips forward and sticks during the short periods immediately after impacts[17].In these initial conditions,the foot of leg 1 never slips on the floor.

4.3 Gait III:Stable periodic gait with bouncing of stance leg

In specific contact parameters and initial conditions of the passive dynamic walker,the stance leg may rebound after switching from as wing leg,which is similar to an elastic collision.Researchers have rarely considered this phenomenon.By choosing the parameters and initial conditions as follows,a stance leg bouncing without slipping is simulated in this paper.

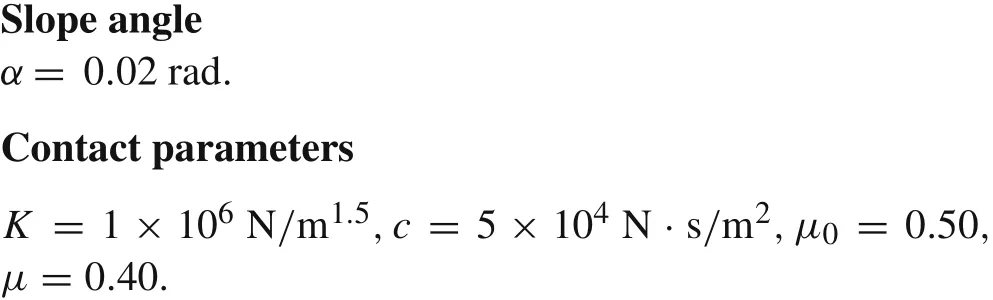
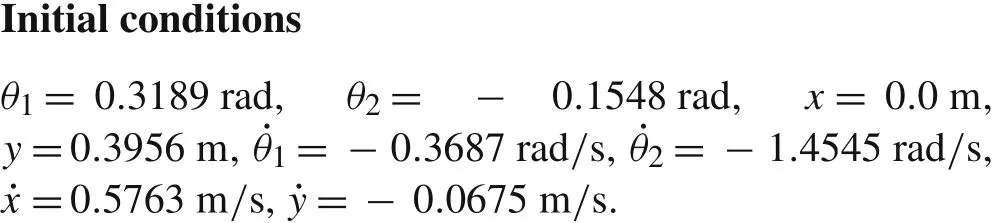
Fig.8 Simulation results of Gait III.a Phase diagrams of θi and(i=1,2);b The trajectory the hip H;c The y-coordinate of the lowest point of each foot;d The normal contact forces acting on each foot

Figure 8a gives the phase diagrams of the swing angles of the two legs.The calculation results show that the two legs of the passive dynamic walker have the same stable periodic gaits,which are different from the gaits shown in Fig.6b.The trajectory of the hipHis depicted in Fig.8b,where we can see that the walker bounces at every step.In order to indicate the stance leg bouncing on the floor more clearly,they-coordinate of the lowest point of each foot,gNi,is given by

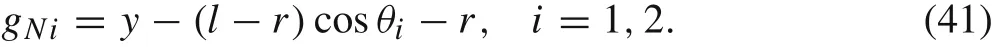
WhengNi＞0,the corresponding penetration depthδi=0,which means that footidoes not touch the floor.WhengNi＜0,the corresponding penetration depthδi= ?gNi＞0,which means footiis or remains in contact with the floor,as shown in Figs.2 and 9.

Fig.9 The y-coordinate of the lowest point of each foot

The time histories ofgNiand the corresponding normal contact forces are illustrated in Fig.8c,d.The region S shows that each stance leg bounces several times after changing from as wing leg.With the initial impact of one leg on the floor at every step,the other detaches from the floor immediately,and a motion in which both feet detach from the floor occurs,as shown in Fig.8c,d.However,this motion still belongs to the “walk”,which is different from the “run”that McGeer studied[40].

4.4 Gait IV:Stance after walking several steps

Fig.10 Simulation results of Gait IV.a Time histories of swing angles;b Time histories of frictional forces

The gaits of the passive dynamic walker are influenced by the slope angle,α.If the slope angle is large or small enough,the passive dynamic walker can barely achieve stable walking.Part of the gravitational potential energy of the walker is transformed into its kinetic energy,and the remainder is dissipated during the contact process between the feet and the floor.If the slope angle is too small,there is not enough gravitational potential energy to be used to walk on the floor,so the walker will fall down or even stand still on the floor.The gait of standing on the floor after walking several steps is simulated by selecting the parameters and initial conditions as follows.Larger frictional coefficients are to prevent the walker from slipping.

Figure 10a gives the time histories of the swing angles of the two legs,which show that after walking a few steps,the passive dynamic walker stands still on the floor.Figure 10b illustrates the time histories of frictional forces acting on the feet.When the walker stands still,the tangential contact forces acting on the feet are static frictional forces which are not zero.

It should be noted that if the modified Coulomb friction law is adopted to describe the tangential contact forces acting on the feet,this gait cannot be simulated,because if the relative tangential velocities of the contact points are zero,the frictional forces are also zero.In our study,the passive dynamic walker can stand still on the floor,so Coulomb’s dry friction model used in this paper can reflect the characteristics of dry friction very well.

5 Conclusions

This paper presented an LCP method for a planar passive dynamic walker with round feet based on an event-driven scheme.First,the normal forces of the contact points were expressed as nonlinear functions of penetration depth and penetration velocity between the feet and floor.In this way,the elastic and dissipative characteristics were well described,and normal forces were not included in the complementarity vectors for the LCP.Therefore,the dimensions of the LCP were reduced,and numerical calculation efficiency was improved.Secondly,Coulomb’s dry friction model was used to describe the tangential frictional forces of contact points.In this way,the stick-slip phenomenon and the static frictional characteristics between the feet and floor were well depicted.Additionally,the dynamic equations of the passive dynamic walker were obtained using the Lagrange equations of the second kind,and the stick-slip transition problem was formulated as an LCP,which was solved using an event-driven scheme.

Four gaits of the passive dynamic walker were simulated to assess the effectiveness of the methodology proposed in this investigation. The numerical results showed that the gaits of the walker were affected by the contact properties and the slope angle of the floor.The walker can realizest able periodic gaits even with slipping or bouncing of the stance leg.If the slope angle is too small,the walker may stand still on the floor after walking several steps.

AcknowledgementsThe project was supported by the National Natural Science Foundation of China(Grants 11372018,11772021).

1.McGeer,T.:Passive dynamic walking.Int.J.Robot.Res.9,62–82(1990)

2.Garcia,M.,Chatterjee,A.,Ruina,A.:Efficiency,speed,and scaling of two-dimensional passive-dynamic walking.Dynam.Stab.Syst.15,75–99(2000)

3.Walsh,C.J.,Paluska,D.,Pasch,K.,et al.:Development of a lightweight,under actuated exoskeleton for load-carrying augmentation.In:IEEE International Conference on Robotics and Automation,ICRA 2006,May 15–19,Orlando,Florida,USA,3485–3491(2006)

4.Collins,S.,Ruina,A.,Tedrake,R.,et al.:Efficient bipedal robots based on passive-dynamicwalkers.Science307,1082–1085(2005)

5.Kuo,A.D.:Biophysics.Harvesting energy by improving the economy of human walking.Science 309,1686–1687(2005)

6.Alexander,M.N.:Walking made simple.Science 308,58–59(2005)

7.Liu,N.,Li,J.,Wang,T.:Passive walker that can walk down steps:simulations and experiments.Acta Mech.Sin.24,569–573(2008)

8.Liu,N.,Li,J.,Wang,T.:The effects of parameter variation on the gaits of passive walking models:simulations and experiments.Robotica 27,511–528(2009)

9.Gritli,H.,Belghith,S.:Computation of the Lyapunov exponents in the compass-gait model under OGY control via a hybrid Poincaré map.Chaos Solitons Fractals 81,172–183(2015)

10.Gritli,H.,Belghith,S.:Bifurcations and chaos in the semi-passive bipedal dynamic walking model under a modified OGY-based control approach.Nonlinear Dyn.83,1955–1973(2016)

11.Gritli,H.,Belghith,S.:Walking dynamics of the passive compassgait model under OGY-based control:emergence of bifurcations and chaos.Commun.Nonlinear Sci.Numer.Simul.47,308–327(2017)

12.Gritli,H.,Belghith,S.:Walking dynamics of the passive compassgait model under OGY-based state-feedback control:Analysis of local bifurcations via the hybrid Poincaré map.Chaos Solitons Fractals 98,72–87(2017)

13.Qi,F.,Wang,T.,Li,J.:The elastic contact influences on passive walking gaits.Robotica 29,787–796(2011)

14.Qi,F.,Bi,L.Y.,Wang,T.S.,et al.:The experimental study on the contact process of passive walking.Acta Mech.Sin.28,1163–1168(2012)

15.Asano,F.:Stability analysis of under actuated compass gait based on linearization of motion.Multibody Syst.Dyn.33,93–111(2015)

16.Asano,F.,Saka,T.,Fujimoto,T.:Passive dynamic walking of compass-like biped robot on slippery downhill.In:IEEE/RSJ International Conference on Intelligent Robots and Systems,Hamburg,Germany,4113–4118(2015)

17.Asano,F.,Saka,T.,Harata,Y.:3-DOF passive dynamic walking of compass-like biped robot with semicircular feet generated on slippery downhill.In:IEEE International Conference on Robotics and Automation(ICRA),Stockholm,Sweden,3570–3575(2016)

18.Asano,F.,Seino,T.,Tokuda,I.,et al.:A novel locomotion robot that slides and rotates on slippery downhill.In:IEEE International Conference on Advanced Intelligent Mechatronics(AIM),Banff,Alberta,Canada,425–430(2016)

19.Pennestrì,E.,Rossi,V.,Salvini,P.,et al.:Review and comparison of dry friction force models.Nonlinear Dyn.83,1785–1801(2016)

20.Gamus,B.,Or,Y.:Dynamic bipedal walking under stick–slip transitions.SIAM J.Appl.Dyn.Syst.14,609–642(2015)

21.Pfeiffer,F.:On non-smooth dynamics.Meccanica 43,533–554(2008)

22.Zhao,Z.,Liu,C.,Chen,B.,et al.:Asymptotic analysis of Painlevé’s paradox.Multibody Syst.Dyn.35,299–319(2015)

23.Zhao,Z.,Liu,C.:Contact constraints and dynamical equations in Lagrangian systems.Multibody Syst.Dyn.38,77–99(2016)

24.Wang,Q.T.,Tian,Q.,Hu,H.Y.:Contact dynamics of elasto-plastic thin beams simulated via absolute nodal coordinate formulation.Acta Mech.Sin.32,525–534(2016)

25.Wang,Q.,Tian,Q.,Hu,H.:Dynamic simulation of frictional multi zone contacts of thin beams.Nonlinear Dyn.83,1919–1937(2016)

26.Zhuang,F.,Wang,Q.:Modeling and simulation of the nonsmooth planar rigid multibody systems with frictional translational joints.Multibody Syst.Dyn.29,403–423(2013)

27.Zhuang,F.F.,Wang,Q.:Modeling and analysis of rigid multibody systems with driving constraints and frictional translation joints.Acta Mech.Sin.30,437–446(2014)

28.Wang,X.,Lv,J.:Modeling and simulation of dynamics of a planarmotion rigid body with friction and surface contact.Int.J.Mod.Phys.B 31,1744021(2017)

29.Duan,W.,Wang,Q.,Wang,T.:Simulation research of a passive dynamic walker with round feet based on non-smooth method.Lixue Xuebao/Chin.J.Theor.Appl.Mech.43,765–774(2011)

30.Johnson,K.L.:One hundred years of Hertz contact.Proc.Inst.Mech.Eng.196,363–378(1982)

31.Johnson,K.L.:Contact mechanics.J.Tribol.108,464(1985)

32.Yigit,A.S.,Ulsoy,A.G.,Scott,R.A.:Spring-dashpot models for the dynamics of a radially rotating beam with impact.J.Sound Vib.142,515–525(1990)

33.Machado,M.,Moreira,P.,Flores,P.,et al.:Compliant contact force models in multibody dynamics:evolution of the Hertz contact theory.Mech.Mach.Theory 53,99–121(2012)

34.Koshy,C.S.,Flores,P.,Lankarani,H.M.:Study of the effect of contact force model on the dynamic response of mechanical systems with dry clearance joints:computational and experimental approaches.Nonlinear Dyn.73,325–338(2013)

35.Wang,Q.,Peng,H.,Zhuang,F.:A constraint-stabilized method for multibody dynamics with friction-affected translational joints based on HLCP.Discrete Cont.Dyn.B 2,589–605(2011)

36.Flores,P.,Leine,R.,Glocker,C.:Modeling and analysis of planar rigid multibody systems with translational clearance joints based on the non-smooth dynamics approach.Multibody Syst.Dyn.23,165–190(2010)

37.Glocker,C.:Set-Valued Force Laws:Dynamics of Non-Smooth Systems.In:Lecture Notes in Applied&Computational Mechanics,Vol.1,Springer-Verlag Berlin Heidelberg(2001)

38.Cottle,R.W.,Dantzig,G.B.:Complementary pivot theory of mathematical programming.Linear Algebra Appl.1,103–125(1968)

39.Leine,R.I.,Campen,D.H.V.,Glocker,C.H.:Nonlinear dynamics and modeling of various wooden toys with impact and friction.J.Vib.Control 9,25–78(2003)

40.M cgeer,T.:Passive bipedal running.Proc.R.Soc.Lond.240,107–134(1990)