A New Calculation of Rotational Bands in Alpha-Cluster Nuclei
N.Roshanbakht and M.R.Shojaei
Department of Nuclear Physics,Faculty of Physics and Nuclear Engineering,Shahrood University of Technology,P.O.Box 36155-316,Shahrood,Iran
1 Introduction
In spite of nuclear systems compliance with quantum mechanical principles,understanding the nature of interparticle bonding forces is crucial for description of a many body system.In this regard,an approximate description of nuclear systems can be achieved by following nuclear physics approaches.One of the popular methods for investigation of nuclear structures is to study their energy spectra.Concentration of rotational bands in the energy spectra of light nuclei such as20Ne and16O is also important.These observations,along with alpha decay from these levels reflect the cluster structure.Previous works have also shown that clustering effects are of crucial importance,in particular for lighter nuclei.[1?5]
Nucleon clustering in the nucleus is one of the interesting topics of nuclear physics. Clustering of the nuclear structure implies that strongly-bound nucleons would form clusters and therefore,the nucleus behaves like a combination of clusters.[6]The advantages of nucleus structure investigation using cluster model are highlighted when the relative motion of clusters becomes the main state of nucleus motion.[7]This phenomenon is based on the increase of the particles energy in the system,which will be followed by reduction of potential energy and increase of nuclei’s stability.In this content,for some nuclei,by increasing energy of the nucleons,they can be regarded as smaller clusters of a mother nucleus.For example,Wuosmaa et al.in 1992,found12C+12C cluster structure in24Mg nucleus.[8]Recently,experimental studies have confirmed cluster structures in Medium-Weight nuclei and cluster structure of36Ar+α was predicted for 40Ca.[9]
In nuclei whose numbers of nucleons are close to those with two magic numbers,valence nucleons can act like a cluster rotating around the magic core. Such cluster structure can present characteristics of rotational spectra.[10?13]For instance,two rotational bands with positive and negative parities exist in20Ne isotopes whose inertial moments are almost the same.Energy of rotational band with negative parity is higher than the positive parity;these bands correspond to rotation of alpha particle around16O cores.Such specific behavior can be also observed in44Ti where alpha particle is rotating around40Ca magic core.
To investigate the clustering phenomenon in nuclei,various models have been proposed.[14?16]However,application of two-particle model including core and cluster is more suitable for studying the rotational levels of nuclei whose clusters are rotating around a core.Through this model,energy spectra of the studied isotopes will be investigated.
2 Calculation of Rotational Bands
So far,numerous methods have been presented for describing the cluster states and calculation of rotational bands e.g.complete shell model[17?18]and Brink-Bloch cluster model.[19]In complete shell model,ground-stateband level would be calculated by considering a singleparticle Hamiltonian.Next by diagonalization of the interactive system of 4 particles out of neutral core,the rest of levels would be calculated.In Brink-Bloch model,alpha particle is considered outside of the core radius,which could be due to large observed widths of alpha.In these models,the potential depth varies for each state.Also,due to numerical processing,potential geometry results could not be guaranteed.Therefore,it is not possible to predict the states whose values have not been measured experimentally.
In this paper,one of the observable properties of nuclei will be precisely calculated and described by consideration of simple assumptions.One assumption is that the components of the structure is alpha particle rotating around a core,which is not necessarily in its ground state.Alpha particle decay formed on the nucleus surface and could be emitted via tunneling.Also,regarding high binding energy and symmetry,it is expected that this cluster can be observed in ground state.Here,by neglecting exchange effects,we will have two real unperturbed nuclei with free properties,which can rotate around each other and create semi-bound states.Therefore,a several-body system can be easily transformed into single-particle system.
Wave functions and energy levels,describing the relative motion of cluster and core,can be obtained by solving Schr?dinger equations through proper selection of principle quantum number,N,and orbital angular momentum,L:

Single particle potential can be defined as V(r)=VN(r)+Vc(r)including a central nuclear potential and a Columbic potential.
For a two-particle system,including a cluster and core,each nucleus can be well described in Su3model.Therefore,by applying Wildermuth condition,shell and cluster models can be related.In other words,given the shell model and Pauli Exclusion Principle,each level would be determined by some quantum numbers where these quantum numbers are also used in the cluster model.This will create a constraint known as Wildermuth condition,which has the following form in its most limited state:[20]
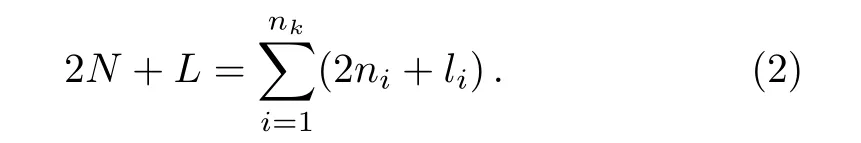
We use this equation as quantum numbers of clusters nucleons related to their internal structure will not be entered into the calculations.In above equation,N and L are the quantum numbers for description of the main nucleus and niand lidenote principle and orbital angular momentum numbers of nucleons composing the cluster.nkshows the cluster nucleons.It must be noted that relative motion with smaller quantum numbers is Pauli-forbidden.Recent studies of Hurichi based on resonance group microscopy(RGM)confirm this model.It was shown that by relying on antisymmetrization,the cluster’s nucleons will occupy the orbitals above the Fermi level.[21?23]
Next,we apply a nuclear potential,which is a combination of Hellmann potential and Deng-Fan potential:
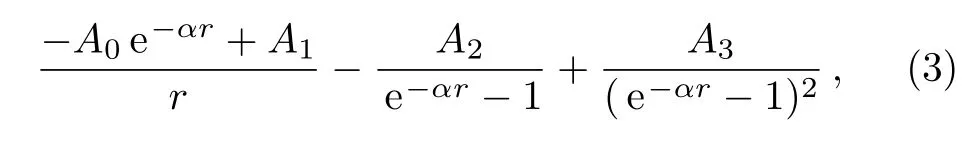
where,A0and A1reflect the strength of each term of potential and α is the screening parameter.Deng-Fan potential has been successful in calculation of two-atom molecules vibrational spectra.[24]It seems that this potential can be also applied in describing nuclei with twocluster structure.Hellman potential is also a combination of Columbic and Yukawa nuclear potential.Therefore,as the experimental results suggest,this combined potential can describe the energy spectra of the studied isotope.
After substitution of central potential(3)in Schr?dinger equation(1)and solving that by Nikiforov-Uvarov(NU)method,[25?27]an eigenvalue equation will be obtained:
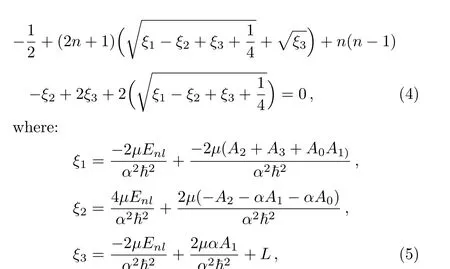
and wave functions of the quantum system will be:
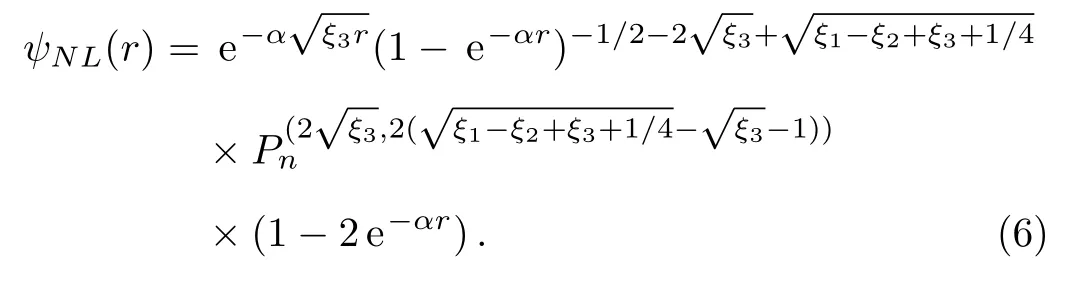
2.1 20Ne Isotope
As the first example of this model,20Ne isotope can be considered as two interactive particles of16O+α.This isotope has an unsymmetrical structure with one rotational band having negative parity and the other rotational band possessing a positive parity.[28]These bands correspond to an alpha particle rotating around a spherical16O core.Hurichi et al.used AMD model to theoretically investigate the clustering degree in different states of20Ne rotational bands.[29]These studies demonstrated a reduction in clustering degree in 8+level of rotational band of ground state.For lower states of the band,isotope has a stretched structure with axial symmetry corresponding to16O+α cluster structure.The cluster structure is completely evident in negative-parity rotational band.For level 7?and above,the tendency to separate the clusters can be observed and emerged in other structures such as12C+α+α.Although these investigations strongly supported cluster structures but they failed to reproduce energy bands of negativeparity bands.
Buck et al.calculated the levels of rotational band of20Ne isotope by considering a two-particle system.[12,30]These calculations,performed through Woods Saxon potential,could not fully reproduce the first states of rotational bands as well as level 7?and above.

Fig.1 Comparison of energy spectra of20Ne with experimental values.[12,17,30?32]
In our model,the lowest assumed level is the ground state of 0+rotational band,which here corresponds to placing 4 nucleons in 1s-0d shell,(2ni+li=2),relative to 0s and 0p.This corresponds to 2N+L=8 in Eq.(2).Calculation of l?rotational bands was conducted with this assumption that there were 3 nucleons in 1s-0d shell and one nucleon went to upper shell 1p-0f;,which resulted in 2N+L=9.Therefore,given the Wildermuth condition and Eq.(4),the first states of rotational bands of 0+and 1?were calculated and then rotational levels were obtained.Calculated energy spectra are shown in Fig.1 and compared with Buck et al.results.It is observed that the head of positive and negative parity bands are located at the ground state and Ex=5.78 MeV,respectively.In this model,α =0.54 fm?1,A0=160.43 MeV,A1=0.83 MeV,A2=10.31 MeV,and A3=6.02 MeV.It can be observed that using our model energy splitting was successfully reproduced in this model.But,calculated value of 8+level has 2 MeV difference with experimental values,which questions cluster structure of this level.
2.2 44Ti Isotope
Based on the investigations,alpha cluster structures are confirmed in light nuclei. But here,by consideration of44Ti isotope as the second example,we will test the performance of the model for the cores with two magic numbers in upper layers;i.e.40Ca where 4 nucleons of valance layer rotate around it in the form of alpha clusters.[30]Therefore,Applied potential is Deng-fan potential combined with Hellman potential whose constants are α =0.74 fm?1,A0=113.20 MeV,A1=21.24 MeV,A2=120.28 MeV,and A3=7.86 MeV.The results for reproducing the levels of two rotational bands with positive and negative parities for44Ti isotope are shown in Fig.2.In Fig.2,we compared our results with the experimental data and the Buck’s results.The bands heads are placed at the ground state and Ex=3.18 MeV in our calculations.The obtained positive-parity bands fits well to the experimental results.This agreement is also observed for negative-parity rotational bands,starting from 3?level.
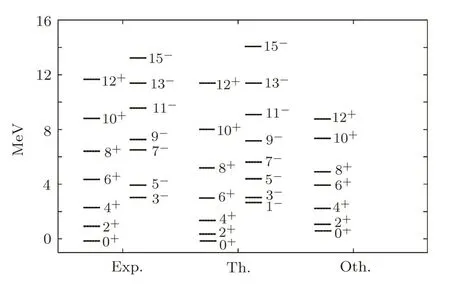
Fig.2 Comparison of energy spectra of44Ti with experimental values.[17,30?32]
In general,the results of44Ti isotope predict denser down-spin states compared to the experimental values.However,the results are better in comparison with Ref.[30].Buck et al.calculated only rotational bands with positive parities,and also their predictions of level 6+and above do not fit well to the experimental data.
3 Conclusion
Here,a model was presented in,which alpha particles act as a cluster in nucleus rather than a series of individual nucleons.Therefore,a several-body problem will be transformed into a single-body problem.By application of Deng-fan potential combined with Hellman potential between the core and shell,proper results were obtained for ground state rotational bands of20Ne and44Ti isotopes.One of the main results of this study is presence of alpha clusters in structure of44Ti isotope and prediction of 1-as the first level of odd-parity rotational band at energy of 2.8 MeV for this isotope.This approach indicates the ability of this simple cluster model in predicting energy levels,which have not been experimentally identified.Moreover,regarding the special characteristics of alpha particles,this model predicts negative-parity bands several mega electron Volts higher than positive-parity ones.
[1]J.A.Maruhn,M.Kimura,S.Schramm,et al.,Phys.Rev.C 74(2006)44311.
[2]R.K.Gupta,S.Kumar,M.Balasubramaniam,et al.,J.Phys.G:Nucl.Part.Phys.28(2002)699.
[3]N.Zoghi-Foumani,M.R.Shojaei,and A.A.Rajabi,Chin.Phys.C 41(2017)14104.
[4]B.Zhou,Z.Ren,C.Xu,et al.,Phys.Rev.C 86(2012)14301.
[5]W.Broniowski and E.R.Arriola,Phys.Rev.Lett.112(2014)112501.
[6]N.D.Cook,Models of the Atomic nucleus,Unification Through a Lattice of Nucleons 2,6(2010)67.
[7]W.Von Oertzen,M.Freer,and Y.Kanada-En’yo,Phys.Rep.432(2006)43.
[8]A.H.Wuosmaa,B.B.Back,I.G.Bearden,et al.,Nucl.Phys.A 553(1993)563.
[9]A.A.Cowley,J.Phys.Conf.Ser.436(2013)12011.
[10]B.Buck,A.C.Merchant,M.J.Horner,and S.M.Perez,Phys.Rev.C 61(2000)24314.
[11]B.Buck,A.C.Merchant,and S.M.Perez,Few-Body Systems 29(2000)53.
[12]B.Buck,C.B.Dover,and J.P.Vary,Phys.Rev.C 11(1975)1803.
[13]B.Buck,J.C.Johnston,A.C.Merchant,and S.M.Perez,Phys.Rev.C 52(1995)1840.
[14]C.Beck,P.Papka,A.Zafra,S.Thummerer,et al.,Clusters in Light Nuclei,arXiv:nucl-ex/1011.3423.
[15]C.A.Bertulani,Nuclear Physics in a Nutshell,Princeton University Press,New Jersey(2007).
[16]M.V.Zhukov,B.V.Danilin,D.Fedorov,et al.,Phys.Reports 231(1993)151.
[17]Y.Akiyama,Nucl.Phys.A 138(1996)273.
[18]E.C.Halbert,J.B.McGrory,and B.H.Wildenthal,Phys.Rev.Lett.20(1968)1112.
[19]Y.C.Tang,Microscopic Description of the Nuclear Cluster Theory,inTopics in Nuclear Physics II A Comprehensive Review of Recent Developments,Springer(1981)pp.571-692.
[20]N.Takigawa and K.Washiyama,Fundamentals of Nuclear Physics,Springer,Tokyo(2015).
[21]H.Horiuchi,J.Phys.Conf.Ser.863(2017)012021.
[22]B.Zhou,Y.Funaki,H.Horiuchi,et al.,Phys.Rev.Lett.110(2013)262501.
[23]Y.Kanada-En’yo,and H.Horiuchi,Prog.Theor.Phys.Supp.142(2001)205.
[24]Z.H.Deng and Y.P.Fan,Journal of Shandong University(Natural Science)1(1957)11.
[25]M.R.Shojaei and N.Roshanbakht,Chin.J.Phys.53(2015)1.
[26]M.Mousavi and M.R.Shojaei,Commun.Theor.Phys.66(2016)483.
[27]A.F.Nikiforov and V.B.Uvarov,Special Functions of Mathematical Physics,Vol.205 Springer,Boston(1988).
[28]P.A.Butler and W.Nazarewicz,Rev.Mod.Phys.68(1996)349.
[29]Y.Kanada-En’yo,M.Kimura,and H.Horiuchi,Comptes Rendus Physique 4(2003)497.
[30]B.Buck,A.C.Merchant,and S.M.Perez,Phys.Rev.C 51(1995)559.
[31]B.Pritychenko,A.A.Sonzogni,D.F.Winchell,et al.,Ann.Nucl.Energy 33(2006)390.
[32]S.M.Wang,J.C.Pei,and F.R.Xu,Phys.Rev.C 87(2013)14311.
 Communications in Theoretical Physics2018年7期
Communications in Theoretical Physics2018年7期
- Communications in Theoretical Physics的其它文章
- Transverse Transport of Polymeric Nano fluid under Pure Internal Heating:Keller Box Algorithm
- Detection of Magnetic Field Gradient and Single Spin Using Optically Levitated Nano-Particle in Vacuum?
- A Numerical Investigation of 3D MHD Rotating Flow with Binary Chemical Reaction,Activation Energy and Non-Fourier Heat Flux?
- Electron Correlations,Spin-Orbit Coupling,and Antiferromagnetic Anisotropy in Layered Perovskite Iridates Sr2IrO4?
- Upshot of Chemical Species and Nonlinear Thermal Radiation on Oldroyd-B Nano fluid Flow Past a Bi-directional Stretched Surface with Heat Generation/Absorption in a Porous Media?
- The Three-Pion Decays of the a1(1260)?
