趙　敏,陳　琴

(中國(guó)計(jì)量大學(xué) 理學(xué)院,浙江 杭州 310018)

1　簡(jiǎn)　介

近三十多年來(lái),圖的控制數(shù)理論已成為圖論的一個(gè)重要研究領(lǐng)域,在相關(guān)學(xué)科領(lǐng)域具有廣泛的應(yīng)用.根據(jù)不同的應(yīng)用背景,人們定義并研究了多種控制參數(shù)[1-9].關(guān)于圖的控制理論的全面研究進(jìn)展可參看文獻(xiàn)[8,9].2002年,Haynes等在文[10]中首先研究了電力網(wǎng)的監(jiān)控問(wèn)題.電力公司為了實(shí)現(xiàn)對(duì)整個(gè)電力網(wǎng)運(yùn)行的監(jiān)控,需要在電力網(wǎng)中選擇一些電力節(jié)點(diǎn)來(lái)放置監(jiān)控設(shè)備(PMU).由于PMU成本的昂貴性,我們希望在保證整個(gè)電力網(wǎng)被完全監(jiān)控的前提下,選擇盡可能少的節(jié)點(diǎn)放置PMU.如果電力網(wǎng)中所有的電力節(jié)點(diǎn)和電力傳輸線都能被放置在電力網(wǎng)中的PMU所監(jiān)控,那么就稱整個(gè)電力網(wǎng)被這些PMU監(jiān)控.Haynes等把這類(lèi)電力網(wǎng)的監(jiān)控問(wèn)題轉(zhuǎn)化到圖論上,發(fā)現(xiàn)它與圖論中經(jīng)典的點(diǎn)覆蓋及控制集問(wèn)題有著密切的關(guān)系.

用G=(V,E)代表整個(gè)電力網(wǎng),G的頂點(diǎn)代表電力節(jié)點(diǎn),邊代表連接兩個(gè)電力節(jié)點(diǎn)的傳輸線.一個(gè)PMU監(jiān)控它所在的電力節(jié)點(diǎn)及與此節(jié)點(diǎn)關(guān)聯(lián)的邊和這些邊的另一個(gè)端點(diǎn)(這些節(jié)點(diǎn)和邊稱為被監(jiān)控).其它被監(jiān)控的規(guī)則如下:

1)如果一條邊被監(jiān)控,則與它關(guān)聯(lián)的點(diǎn)也被監(jiān)控;

2)如果兩個(gè)相鄰的點(diǎn)被監(jiān)控,則連接這兩點(diǎn)的邊也被監(jiān)控;

3)如果一個(gè)點(diǎn)與k條邊關(guān)聯(lián)(k>1),并且這k條邊中有k-1條被監(jiān)控,則這k條邊都被監(jiān)控.我們稱電力控制集具有“傳遞性”.

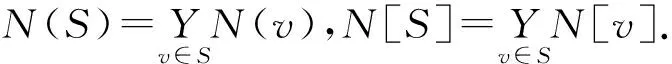
設(shè)S?V(G),若N[S]=V(G),則稱S為圖G的控制集.最小控制集的基數(shù)稱為控制數(shù),記為γ(G).基數(shù)恰為γ(G)的控制集稱為G的γ(G)-集.若S為G的控制集,則稱S控制圖G.根據(jù)電力網(wǎng)中特定的“監(jiān)控”規(guī)則,Hayne等[9]定義了電力控制集的概念.設(shè)S?V(G)是監(jiān)控集,如果G的所有點(diǎn)和邊都被監(jiān)控,則稱S為G的電力控制集,最小電力控制集的基數(shù)稱為電力控制數(shù),記為γP(G).基數(shù)恰為γP(G)的電力控制集稱為G的γP(G)-集.若S為G的電力控制集,則稱S電力控制圖G.文中其它未加定義的術(shù)語(yǔ)和記號(hào)可參看文獻(xiàn)[8]和[9].

本文將研究平方圖的電力控制集問(wèn)題,給出幾類(lèi)電力控制數(shù)為1的平方圖.

2　主要結(jié)果

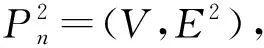
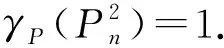
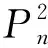
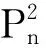
設(shè)圈

C

n

=(

V

,

E

),其中

V

={

v

1

,

v

2

,…,

v

n

},

E

={

v

i

v

i+1

|

i

=1,2,…,

n

}.則

其中

E

2

={

v

i

v

i+1

,

v

i

v

i+2

|

i

=1,2,…,

n

},這里點(diǎn)的下標(biāo)取

n

的模.如圖2所示.

圖2　圖

類(lèi)似定理2.1,可以證明以下結(jié)果:

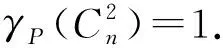
關(guān)于路與圈的k次方圖的電力控制數(shù),我們有下列結(jié)果:

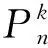
下面我們討論平方格子圖的電力控制數(shù).圖P2□Pn與P3□Pn的平方圖如圖3.我們有下列結(jié)果:

定理2.4:設(shè)Pn是階數(shù)為n≥2的路.那么γP((P2□Pn)2)=1.

證明:設(shè)D={(1,2)},則D監(jiān)控N[(1,2)]={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3)}(圖3(a)中黑色的點(diǎn)).對(duì)于N[(2,2)]={(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(2,4)}中的點(diǎn),除了點(diǎn)(2,4)外,其余點(diǎn)均被D監(jiān)控,所以(2,4)也被D監(jiān)控.同理,對(duì)每個(gè)i=1,2,j=3,4,…,n-2,N[(i,j)]中的點(diǎn),除了點(diǎn)(i,j+2),其余點(diǎn)均被D監(jiān)控,所以(i,j+2)也被D監(jiān)控.因此,D是平方圖(P2□Pn)2的電力控制集,即γP((P2□Pn)2)=1.

圖3　P2□Pn與P3□Pn的平方圖Figure 3　The square graphs of P2□Pn and P3□Pn

定理2.5:設(shè)Pn是階數(shù)為n≥3的路.那么γP((P3□Pn)2)=1.

證明:設(shè)D={(2,2)},則D監(jiān)控N[(2,2)]={(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3)}(圖3(b)中黑色的點(diǎn))對(duì)于N[(1,2)]中的點(diǎn),除了點(diǎn)(1,4)外,其余點(diǎn)均被D監(jiān)控,所以(1,4)也被D監(jiān)控.同理,對(duì)于N[(3,2)]中的點(diǎn),除了點(diǎn)(3,4)外,其余點(diǎn)均被D監(jiān)控,所以(3,4)也被D監(jiān)控.依次考察i=2,1,3,對(duì)每個(gè)j=3,4,…,n-2,因?yàn)镹[(i,j)]中的點(diǎn),除了點(diǎn)(i,j+2),其余點(diǎn)均被D監(jiān)控,所以(i,j+2)也被D監(jiān)控.因此,D是平方圖(P3□Pn)2的電力控制集,即γP((P3□Pn)2)=1.