Axial laminar velocity field calculation and optimization for power-law fluid in eccentric annulus with cutting bed *
Yong-hai Gao (高永海), Ye Chen (陳野), De-jun Cai (蔡德軍), Hua-qing Liu (劉華清),Cheng-gui Liu (劉承貴), Qing-yong Li (李慶永)
1. School of Petroleum Engineering, China University of Petroleum (East China), Qingdao 266580, China
2. National Engineering Laboratory for Testing and Detection Technology of Subsea Equipments, Qingdao 266101, China
3. Drilling Department, CNPC Offshore Engineering Company Limited, Tianjin 300280, China
Abstract: The formation of a cutting bed in an annulus involves safety problems in drilling especially in the horizontal well and the directional well.In this work, three axial laminar velocity field calculation models for the power-law fluid in an annulus are modified by considering the effect of the cutting bed.The proposed models are employed to numerically simulate the annulus flow with the cutting bed.Verified by the experimental data in literature, all of them can be applied to the situation of the annulus flow with the cutting bed.The modified concentric annulus model enjoys the best performance, while the flat channel flow model has the worst performance.
Key words: Eccentric annulus, power-law fluid, axial laminar velocity field, cutting bed
Introduction
The power-law fluid is a kind of non-Newtonian fluid which is widely used in the oil and gas industry[1-3].In the horizontal well and directional well drilling, the majority of the annulus is eccentric due to the gravity of the drilling string.In that case, the flow in the wellbore is an eccentric annulus flow[4-5].The eccentric annulus flow may lead to the formation of a cutting bed[6-7].Therefore, the velocity field for a power-law fluid in an eccentric annulus is a research focus of practical significance for the drilling safety.
In order to seek a reliable method for the design of the hydraulic parameters of the horizontal well and the directional well, unremitting efforts were made in the past decades[8-12].As the eccentric annulus can make the flow region irregular and the constitutive equation of the power-law fluid is nonlinear, it is very difficult to calculate the related parameters.At present,most calculations were based on an approximate method to meet the engineering needs.Among these calculations, the CFD simulation software can be used for the numerical simulation of the velocity field in an eccentric annulus.However, the calculation time is too long and the calculation method is not transplantable, which make it inconvenient in the field application[13].Therefore, it is desirable to find a numerical method to simulate the velocity field in an eccentric annulus accurately.
In this work, three models (the approximate analysis formula model, the flat channel flow model and the concentric annulus model) for the power-law fluid flow in an eccentric annulus are modified to take into account the effect of the cutting bed.Based on this, the axial laminar velocity field calculation models for the power-law fluid in an eccentric annulus with a cutting bed are proposed.Using the numerical calculation method, the models are implemented and the velocity profiles are calculated.The accuracy of the different flow models is analyzed by comparing with the experimental data in literature[14].
1.Numerical model of power-law fluid flowing in annulus
Figure 1 shows a schematic diagram of the cross section of an eccentric annulus with a cutting bed.In Fig.1,Riis the inner radius,R0is the external radius,eis the eccentricity of the inner tube and the outer tube,Rhis the distance from the axle center of the inner tube to the outer tube wall and the cutting bed.The dotted ring is composed by the maximum peak points of the velocity.Rpis the radius of the dotted ring.The value ofRpis variable.
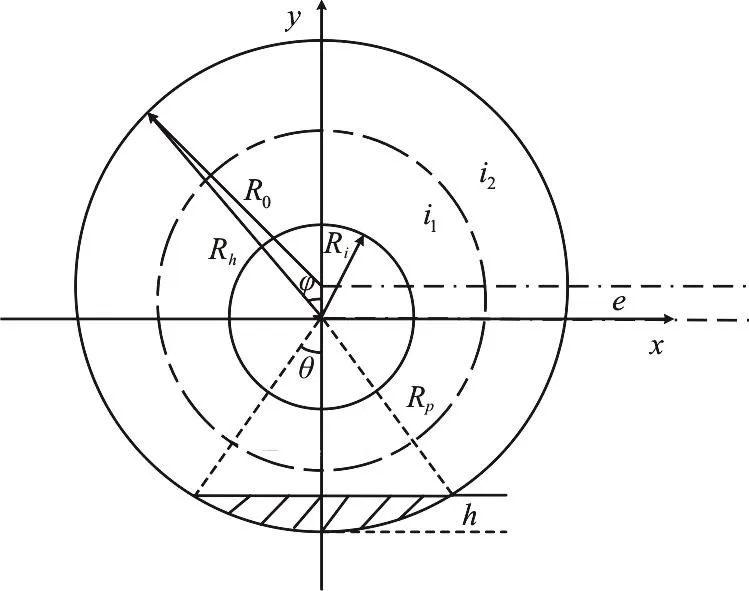
Fig.1 Schematic diagram of the cross section of eccentric annulus with cutting bed
According to the geometric relations, we have

whereR0is the external radius,eis the eccentricity of inner tube and outer tube,his the height of cutting bed,Rhis the distance from axle center of inner tube to outer tube wall and cutting bed.
Assume thatiis an arbitrary point in the eccentric annulus.For the axial direction constant flow, the stress analysis ofiinzaxis is shown in Fig.2, and the summation of forces is

whereFzis the force inzdirection.

Fig.2 Stress analysis of i in the z axis
is an element on the ring.Projecting the force in all directions ofi1to thezaxis, from Eq.(4), we obtain
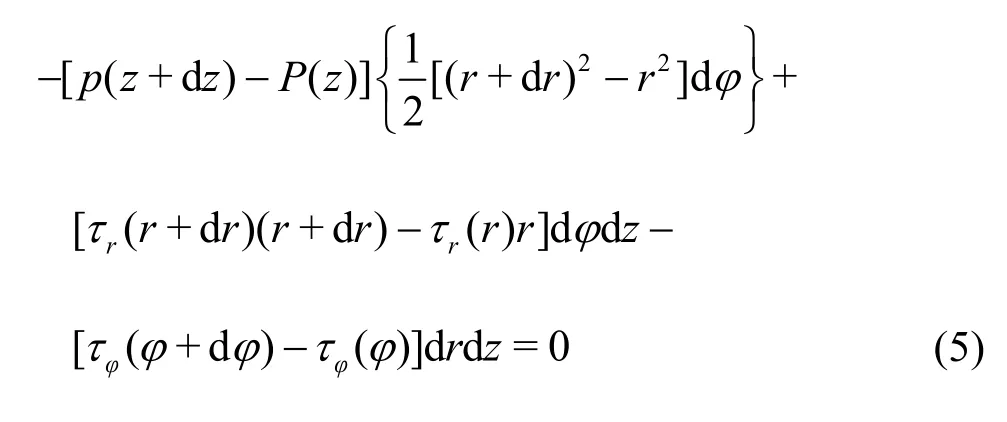
Divide the above equation byrdrdwdzand take the limit, we have

wherepis the pressure,τis the apparent viscosity.
Likewise, the formula for elementi2out of the ring is

In the cylindrical coordinate system for the axial steady laminar fluid in the eccentric annulus, the differential equations of motion are Eqs.(6), (7).
According to the ideal situation, the velocity distribution of the flow field is assumed as(0,0,u(r,φ)).Apparent viscosity calculation formula for the power-law fluid can be obtained as
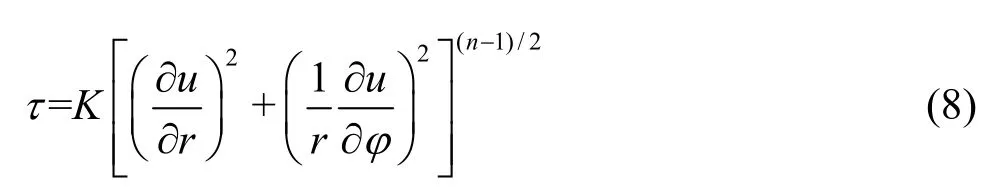
whereKis the consistency coefficient of the power-law fluid,nis the flow behavior index.
In addition, there is no slip on the wall, so the boundary conditions are

Equations (6)-(10) are a quasi-linear elliptic equation set, whose solution region is an irregular eccentric annulus.The solution is considerably difficult.Therefore, a variety of simplified calculation methods were proposed[15-20].Among these methods, the approximate analysis formula model and the flat channel flow model are the most popular.
2.Simplified models
2.1 Approximate analysis formula model
In the approximate analysis formula model[15],the existence of the cutting bed is not taken into account and the term -?τφ|r?φis ignored.A further analysis shows thatτr|ris also ignored.So,the axial laminar velocity field for a power-law fluid in an eccentric annulus is written as:

2.2 Flat channel flow model
In the flat channel flow model[16], the existence of the cutting bed is not taken into account.The floating space of the eccentric annulus is expanded into a flat channel with a variable heighth, and ath/ 2 the maximum velocity of the flat flow is supposed to reach, as shown in Fig.3
Consider a flow field with an arbitrary heighthand a width dφas the flat flow.Its velocity distribution is shown in Fig.4
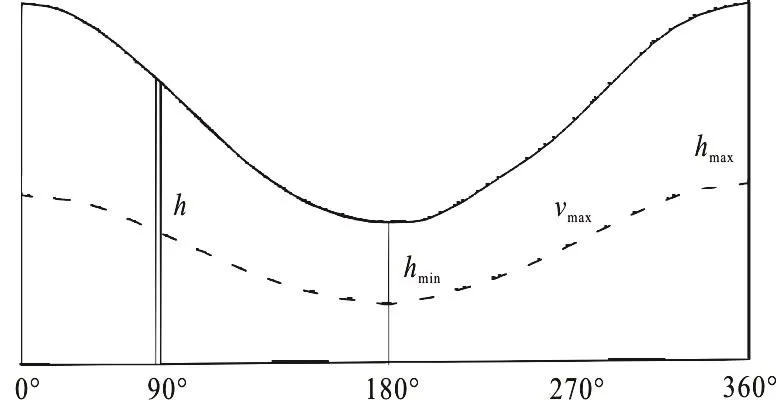
Fig.3 Flat plate diagram with variable height h

Fig.4 Velocity distribution of flat plate laminar flow
Then the velocity field distribution is as follows

2.3 Concentric annulus model
In 1987, Peden and Luo suggested that the eccentric annulus can be considered as a series of concentric annuluses with a constant inner diameter and a variable outer diameter[17].This model transforms the power-law flow problem in an eccentric annulus into that in a concentric annulus.Finally, the model is simplified by letting ?u/?φ= 0.

The general solution of Eq.(13) is

With the boundary conditionτr(Rp) =0, the integral constant, we have

Substituting Eq.(15) into Eq.(8), we have

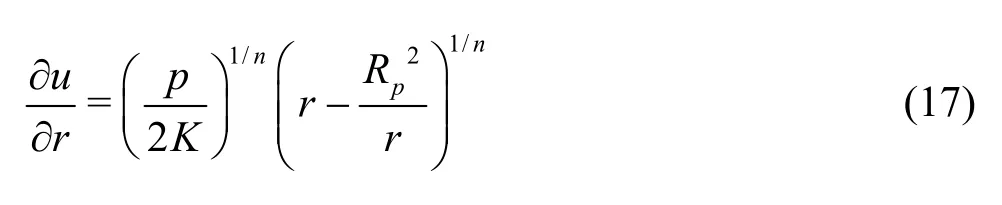
wherenis the flow behavior index.As 0≤n≤1,Eqs.(16), (17) cannot be solved in elementary functions.Therefore, the model is solved by a numerical method.
3.Model modification and numerical implementa tion
None of the above models has taken the effect of the cutting bed into consideration.In this paper, these three models are modified by taking into account the actual situation of the cutting bed.
First of all, the whole ring is divided into three regions.Each region is equally divided intoNparts, and calculated by the numerical method.

wherej=0,1,2,3…3N.
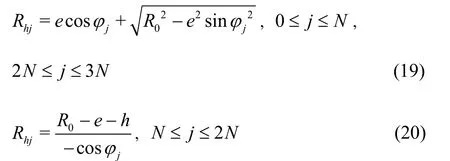
3.1 Modification on approximate analysis formula model
The approximate analysis formula model is modified, within Eqs.(6), (7)ignored, andregarded as the position of the maximum velocity.ForRhjat a general position,the calculation equation of the velocity distribution can be expressed as:

3.2 Modification on flat channel flow model
In the modification of the flat channel flow model, the eccentric annulus is expanded into an arc groove, withRhjeverywhere as a flat flow, andis regarded as the position of the maximum velocity.The velocity distribution can be obtained as
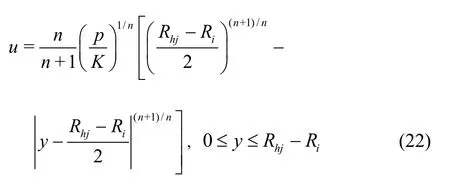
3.3 Modification on concentric annulus model
In order to modify the concentric annulus model,first of all, the maximum velocity for eachNat the position of
should be calculated instead of using the approximate method by taking the value at the middle position in the concentric annulus as the maximum velocity.


Table1 Calculated flow rate and error for different eccentricities
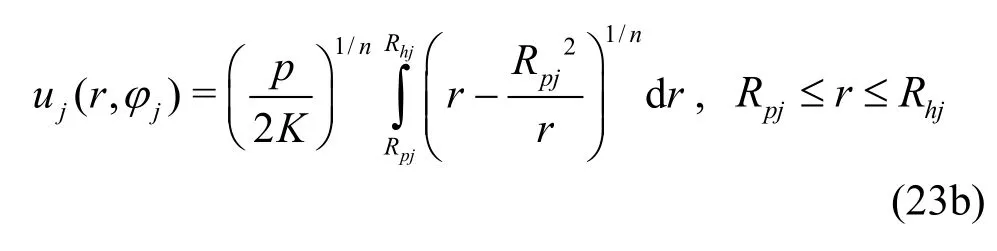
whereRpjis the position of the maximum velocity at(Ri,Rhj), which satisfies the following continuity equation of the power-law fluid

Equations (23) involves a complex integral, with the dependent variable not only in the integrand, but also in the upper and lower limits of the integral.So the analytical solution cannot be obtained.Using the numerical method to calculate eachRpj(with a predetermined calculation accuracy) and the velocity fielduj(r,φj).Then the flow rateQin the whole eccentric annulus can be calculated by these three models with the numerical integration.
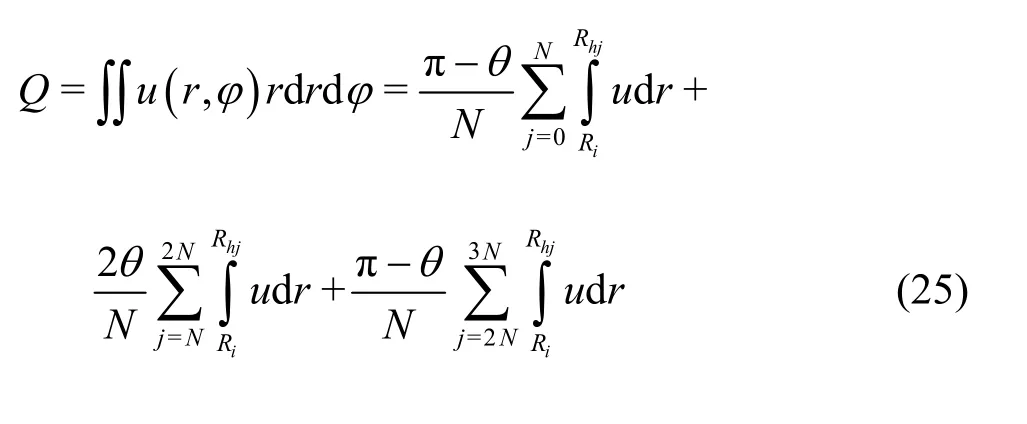
4.Main results and discussions
4.1 Comparison of the three modified models
In order to verify the reliability of the model, the existing examples of takinghas 0 are adopted to do a comparative analysis[17].The wellbore diameter is 0.1 m, the drilling string diameter is 0.07 m, the consistency coefficient is 0.05 Pa?Sn, the flow behavior index is 0.81, and the pressure gradient is 240 Pa/m.The calculation results are shown in Table1.
From the above table, it is obviously seen that the results of three improved models are very close to those of existing examples.The error of the concentric annulus model is the smallest, followed by the approximate analysis formula model, and the flat channel flow model is the last.
4.2 Comparative results of calculation and experiment
We compare the calculated results using the improved models with those of the examples in the published literature, verified by experiments[14,18].
The wellbore diameter is 0.1270 m, the drilling string diameter is 0.0508 m, the eccentricity is 0.0250 m, the consistency coefficient is 0.2638 Pa?Sn,the flow behavior index is 0.736, and the pressure gradient is 120.6474 Pa/m.According to the experiment,the average linear velocity maintains as 0.5822 m/s.At this moment, a laminar flow is formed and its flow rate is 0.0248 m3/s.The calculated flow rates and errors of three models are listed in Table2.Obviously,in this paper, the concentric annulus model is more accurate than the others.
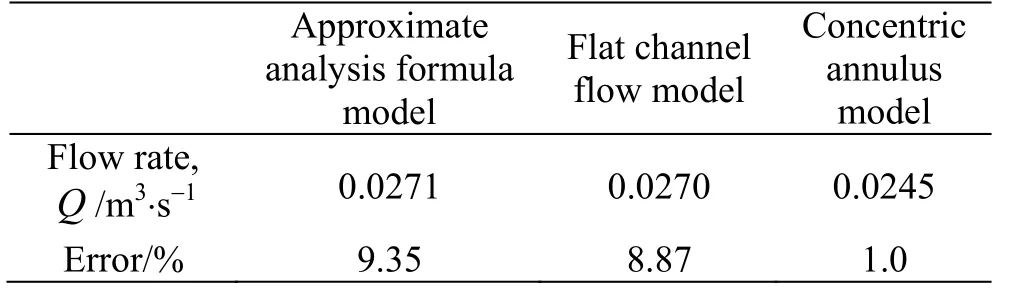
Table2 Calculated flow rate and error of three models
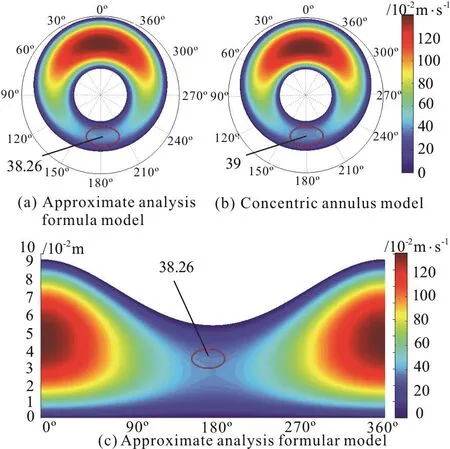
Fig.5 (Color online) Velocity distribution cloud pictures of three models
According to the velocity profiles obtained by using the concentric annulus model, the flat channel flow model and the approximate analysis model in this example, in the red oval area, the calculated velocity field results by using the approximate analysis model and the flat channel flow model are very close.The maximum velocities obtained by using the approximate analysis model and the flat channel flow model are both 0.3826 m/s at 180°.By using a more accurate concentric annulus model, its maximum velocity is 0.3900 m/s at 180°.The velocity distribution cloud of the three models are shown in Fig.5.
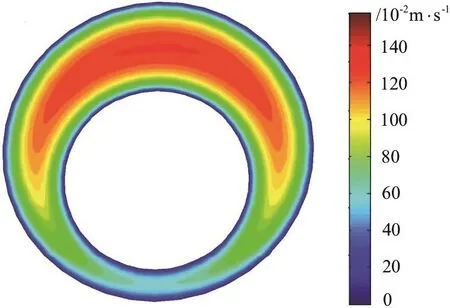
Fig.6 (Color online) Velocity distribution cloud picture calculated by Fluent (CFD software)

Fig.7 (Color online) Velocity cloud pictures obtained by using three models with 0.4 in cutting bed
In addition, the velocity profile calculated by using the Fluent, a common CFD software for hydromechanics, is shown in Fig.6.It indicates that the velocity distributions obtained by using the three models are similar to that obtained by using the Fluent.However, the calculations by using the three models are much easier than by using the CFD software and take a shorter calculation time.
Based on the analysis without the cutting bed,several experiments with various cutting bed thicknesses of 10.16 mm, 20.32 mm and 25.40 mm have been performed[19].The flow rate is kept as 0.0248 m3/s, the pressure drop is 122.1555 Pa/m, 123.6636 Pa/m and 124.4177 Pa/m, respectively.A comparison of the results between the predictions obtained by using the three modified models and the experimental results is shown in Table3.
According to Table3, the most accurate model is the concentric annulus model, the next is the approximate analysis formula model, while the last one is the flat channel flow model.
According to the velocity profiles predicted by the concentric annulus model, the flat channel flow model and the approximate analysis model with a cutting bed thickness of 10.16 mm, the calculated velocity fields see a good agreement between the approximate analysis model and the flat channel flow model in the red oval area.The maximum velocities obtained by using the approximate analysis model and the flat channel flow model are both 0.1809 m/s at 180°.By using the more accurate concentric annulus model, the maximum velocity is 0.1835 m/s at 180°,as shown in Fig.7.
5.Conclusions
In the present study, three modified models, the approximate analysis formula model, the flat channel flow model and the concentric annulus model, for the axial laminar velocity field calculation of power-law fluid in an annulus are developed.The published experimental tests are employed to verify these three models, and the main conclusions can be drawn as follows:
(1) The eccentric annulus power-law flow model can be applied to analyze the horizontal wellbore flow field with a cutting bed.Its calculated results are close to those obtained by using the CFD software, and its use is much easier and takes a shorter time.
(2) For the eccentric annulus flow with a cutting bed,
the calculation result obtained by using theconcentric annulus model is the most accurate with the largest maximum velocity at 180o, followed by the approximate analysis model and the flat channel model.

Table3 Calculation flow rate and error obtained by using three improved models with different cutting bed thicknesses
 水動(dòng)力學(xué)研究與進(jìn)展 B輯2018年5期
水動(dòng)力學(xué)研究與進(jìn)展 B輯2018年5期
- 水動(dòng)力學(xué)研究與進(jìn)展 B輯的其它文章
- Call For Papers The 3rd International Symposium of Cavitation and Multiphase Flow
- Improving the real-time probabilistic channel flood forecasting by incorporating the uncertainty of inflow using the particle filter *
- A selected review of vortex identification methods with applications *
- Tracer advection in an idealised river bend with groynes *
- Simulation of the overtaking maneuver between two ships using the non-linear maneuvering model *
- The effect of downstream resistance on flow diverter treatment of a cerebral aneurysm at a bifurcation: A joint computational-experimental study *
