Kinetic Simulation of Nonequilibrium Kelvin-Helmholtz Instability?
Chuan-Dong Lin(林傳棟) Kai H.Luo? Yan-Biao Gan(甘延標(biāo))and Zhi-Peng Liu(劉枝朋)
1Center for Combustion Energy,Key Laboratory for Thermal Science and Power Engineering of Ministry of Education,Department of Energy and Power Engineering,Tsinghua University,Beijing 100084,China
2Department of Mechanical Engineering,University College London,Torrington Place,London WC1E 7JE,UK
3North China Institute of Aerospace Engineering,Langfang 065000,China
4Department of Physics,School of Science,Tianjin Chengjian University,Tianjin 300384,China
AbstractThe recently developed discrete Boltzmann method(DBM),which is based on a set of uniform linear evolution equations and has high parallel efficiency,is employed to investigate the dynamic nonequilibrium process of Kelvin-Helmholtz instability(KHI).It is found that,the relaxation time always strengthens the global nonequilibrium(GNE),entropy of mixing,and free enthalpy of mixing.Specifically,as a combined effect of physical gradients and nonequilibrium area,the GNE intensity first increases but decreases during the whole life-cycle of KHI.The growth rate of entropy of mixing shows firstly reducing,then increasing,and finally decreasing trends during the KHI process.The trend of the free enthalpy of mixing is opposite to that of the entropy of mixing.Detailed explanations are:(i)Initially,binary diffusion smooths quickly the sharp gradient in the mole fraction,which results in a steeply decreasing mixing rate.(ii)Afterwards,the mixing process is significantly promoted by the increasing length of material interface in the evolution of the KHI.(iii)As physical gradients are smoothed due to the binary diffusion and dissipation,the mixing rate reduces and approaches zero in the final stage.Moreover,with the increasing Atwood number,the global strength of viscous stresses on the heavy(light)medium reduces(increases),because the heavy(light)medium has a relatively small(large)velocity change.Furthermore,for a smaller Atwood number,the peaks of nonequilibrium manifestations emerge earlier,the entropy of mixing and free enthalpy of mixing change faster,because the KHI initiates a higher growth rate.
Key words:discrete Boltzmann method,Kelvin-Helmholtz instability,nonequilibrium effect
1 Introduction
The Kelvin-Helmholtz instability(KHI),named after Lord Kelvin and Hermann von Helmholtz,arises at the perturbed interface between fluids in shear motion,and leads to the formation of vortices and turbulence.[1?2]KHI phenomena are ubiquitous in nature and engineering.[3?5]Examples include waves on a windblown ocean or sand dune,swirling cloud billows,the stream structure of solar corona,the helical wave motion in ionized comet tails,the Great Red Spot in Jupiters atmosphere,the Eagle Nebula in astrophysics,the reacting mixing layers in combustion,and the ignition in inertial confinement fusion.The KHI is one of the most fundamental and famous instabilities in fluid dynamics,and it is often coupled with other instabilities,such as Rayleigh-Taylor instability,[6?7]Richtmyer-Meshkov instability,[8?9]etc.Hence,due to its great importance,the KHI has been studied extensively in experimental,[7,10?11]theoretical,[6]and numerical fields.[12?13]
Particularly,with the rapidly improving computational facilities and algorithms,numerical simulation has achieved more and more successes in scientific research and engineering application. Roughly speaking,there are three kinds of numerical methods:microscopic,[14?15]mesoscopic,[13,16]and macroscopic approaches,[17]respectively. Microscopic models,such as molecular dynamics[14]and direct simulation Monte Carlo,[15]describe the location and motion of particles in detail,but usually demand too high computational cost.Macroscopic schemes,such as direct numerical simulation,large eddy simulation,and Reynolds-averaged Navier-Stokes(NS)equations,improve computational efficiency significantly,but lose various thermodynamic nonequilibrium information which plays an essential role in interfacial dynamics.To reach a compromise between the computational cost and physical fidelity,a promising method is mesoscopic kinetic modelling based on the Boltzmann equation.
In the last three decades,the kinetic-based lattice Boltzmann method(LBM)[18?20]has been developed and become a powerful tool for investigating coherent structures and detailed nonlinear dynamics of complex flows,including the KHI.[21?26]However,most researchers were more likely to take the LBM as a numerical solver of hydrodynamic equations rather than a kinetic model of nonequilibrium systems.Therefore,little consideration has been given to the kinetic nature of related systems.As a novel variant of the LBM,the discrete Boltzmann method(DBM)overcomes the above issue.[27?32]It has the capability of simulating the dynamic process of KHI properly by incorporating essential nonequilibrium effects.[27?32]In 2011,Ganet al.proposed a kinetic model for compressible systems and studied the KHI under the influence of velocity and density gradients.[27]This model recovers the Euler equations in the continuum limit,and works for single-component flows.In 2016,Linet al.developed a DBM for two-component systems.[31]This model recovers the compressible NS equations when the Knudsen number approaches zero,[31]and provides more accurate physical information than the former.[27]In the current work,we employ the two-component DBM to study the nonequilibrium process of KHI.
This paper is organized as follows:In Sec.2,we introduce the DBM that provides detailed nonequilibrium information and high parallel efficiency.In Sec.3,we use the DBM to study the nonequilibrium effects,entropy of mixing,and free enthalpy of mixing in the KHI process.Finally,conclusions are given in Sec.4.
2 Discrete Boltzmann Model
The discrete Boltzmann equations with single collision term take the form,

wheretindicates the time,vkithe discrete velocity,σthe fl uid species,the discrete(equilibrium)distribution function,andτσthe relaxation time.Note that,for a two-component system(σ=AandB),the relaxation of the two species should be equal in order to ensure the local momentum conservation,i.e.,τA=τB=τ.[33]The relaxation time is specified as a function of species concentration in Ref.[33].For simplicity,it is given a constant value here.Additionally,two-dimensional simulations are carried out in the present study,although the formulation can be easily extended to three dimensions.We adopt the second Runge-Kutta scheme for the time derivative and the second order nonoscillatory and nonfree-parameter dissipative finite difference scheme[34]for the space derivatives in Eq.(1).
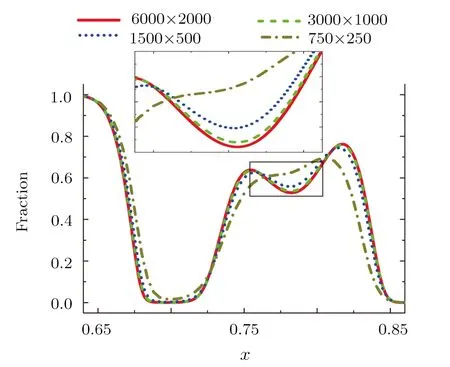
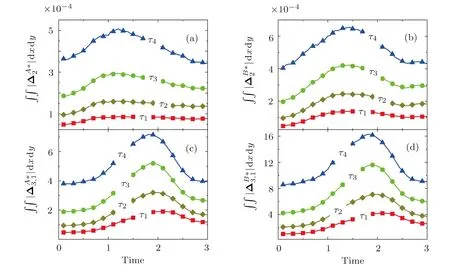
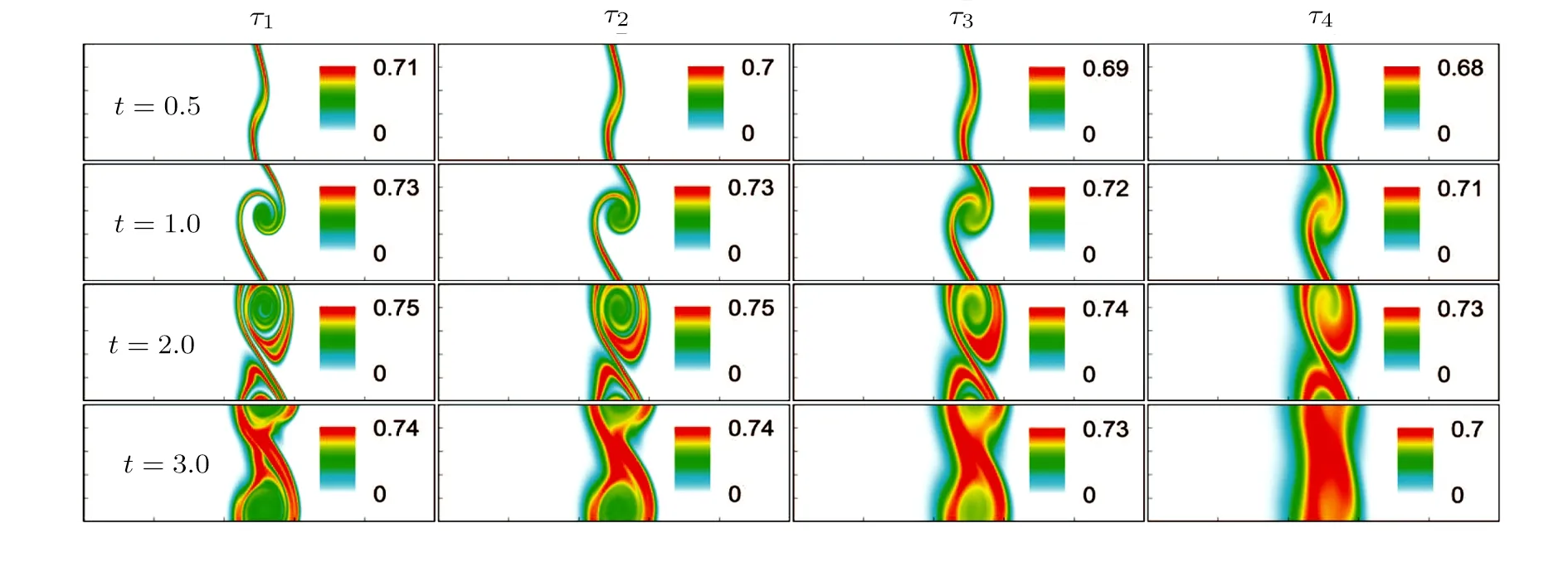
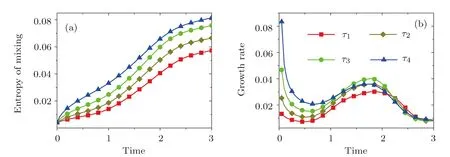
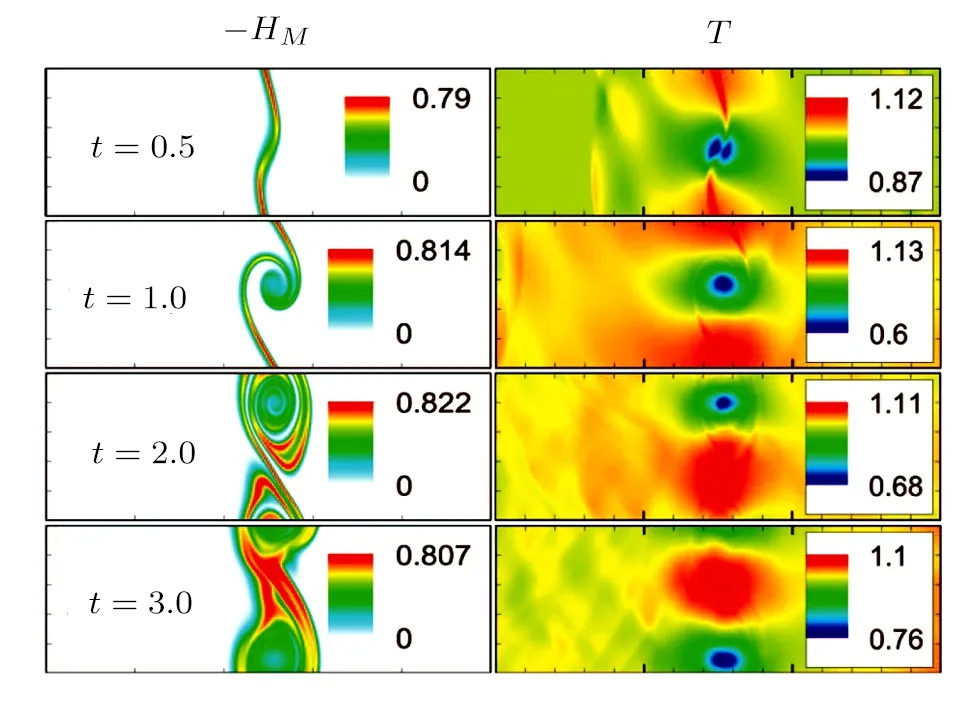
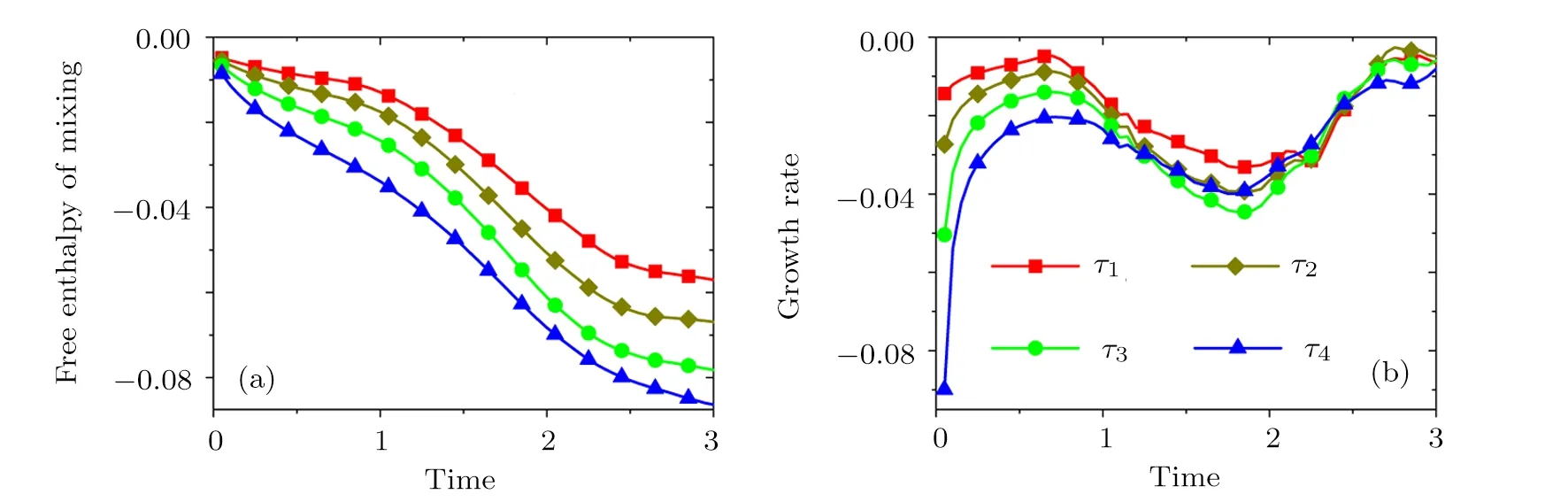
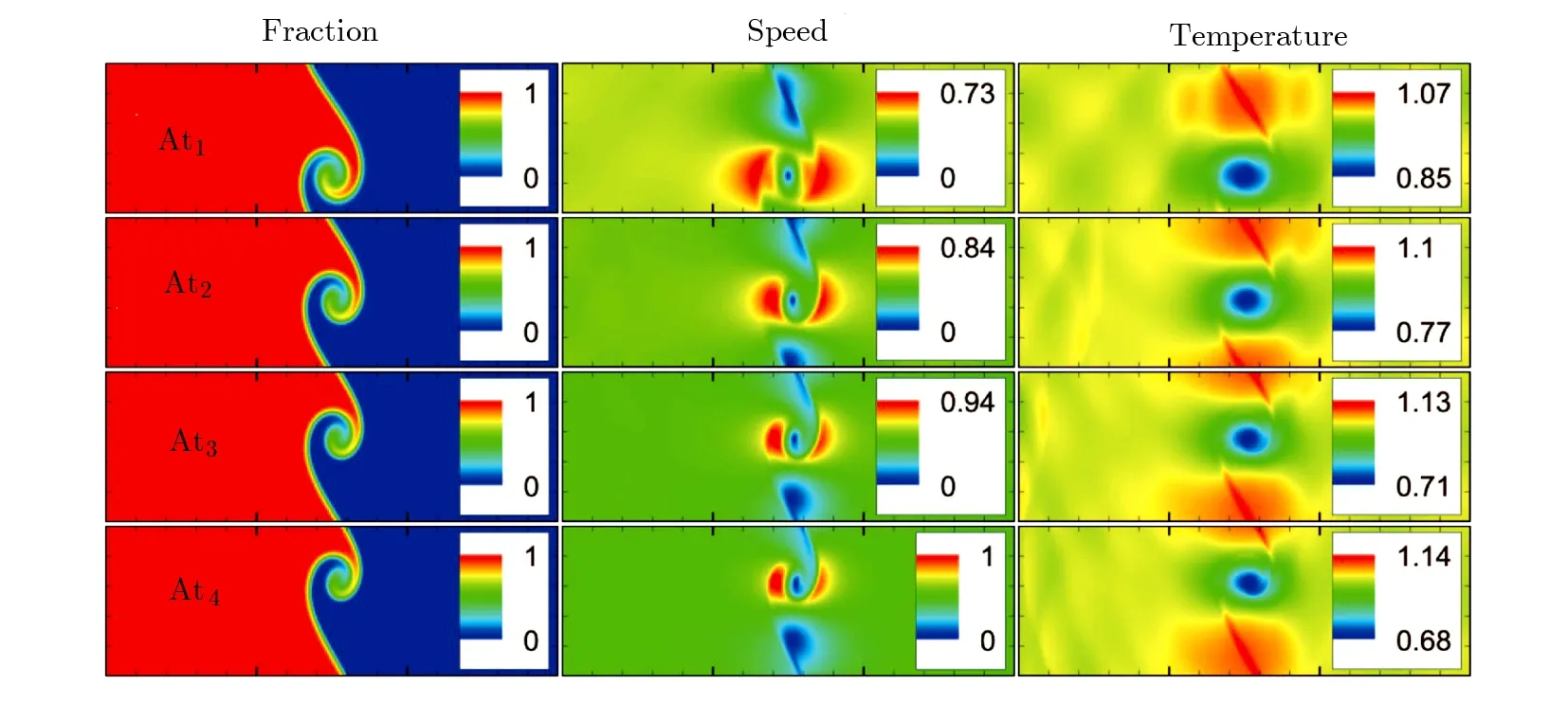
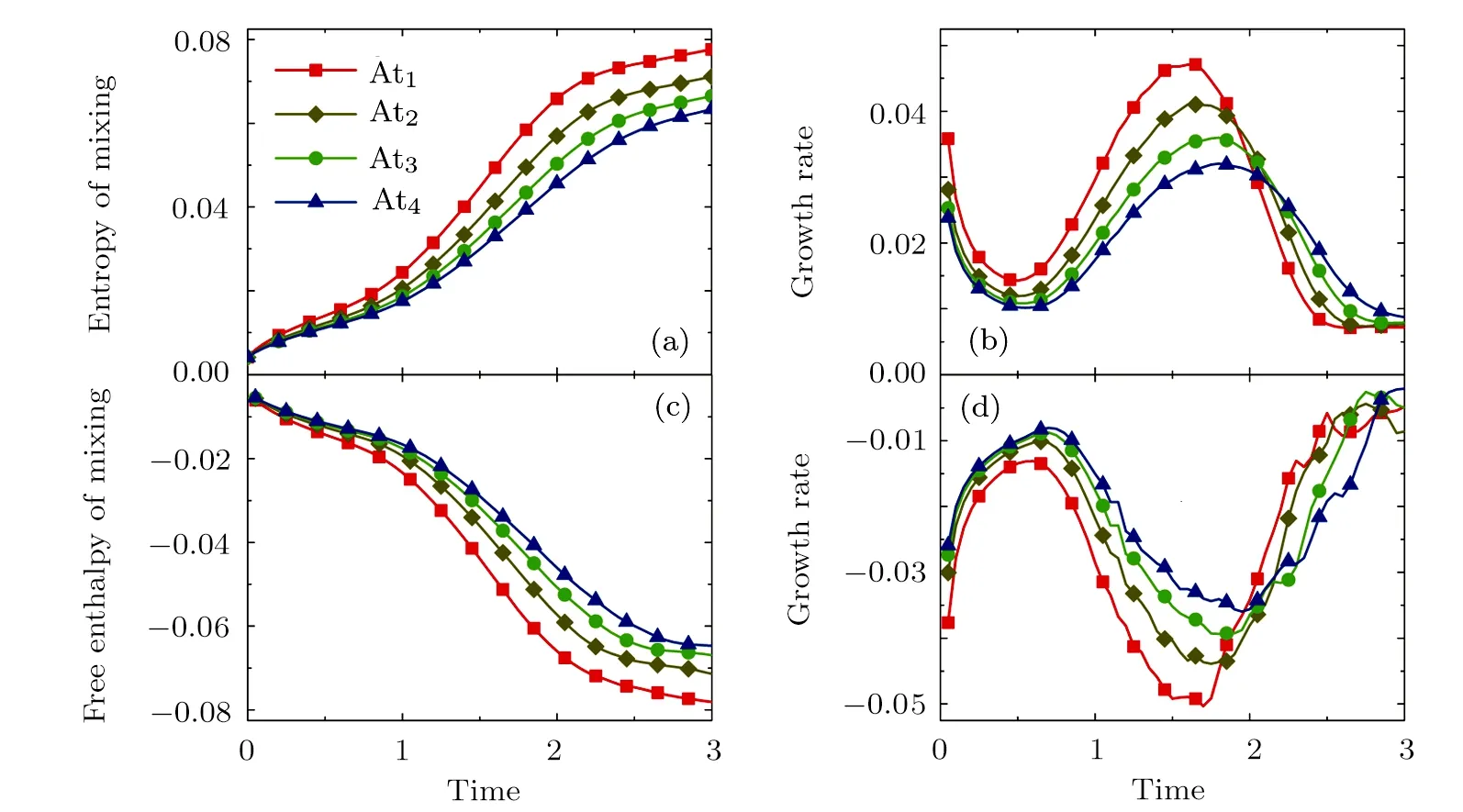
The discrete velocity reads,vki=vkixex+vkiyey,withvkix=vkcos(2πi/8),vkiy=vksin(2πi/8).The suffixiindicates the direction of the discrete velocity,andkindicates thek-th group of the particle velocities whose speed isvk.To be specific,i=1,2,...,8 andk=0,1,...,4.To ensure the simulation robustness,an optimal choice is 0=v0 Fig.1 Sketch of the discrete-velocity-model. The expression ofreads, with the flow speedu,andθσ=T/mσ,wheremσrepresents the molar mass,Tthe temperature.The weighting coefficients are, where the suffixes The mole concentration,mass density,flow velocity,and energy of speciesσare calculated as below The mole concentration,mass density,flow velocity and temperature of the mixing areandrespectively.Mathematically,the coupling between the Boltzmann equations for the two species is achieved achieved via the flow speedu=|u|and temperatureTwhich enter the expression of the equilibrium distribution functions in Eq.(2).In this way,the cross-collisions of speciesAandBexchange physical information between them. It is easy to prove that the DBM could recover the NS equations in the hydrodynamic limit.[31]Moreover,the DBM can be employed to measure the following nonequilibrium manifestations, Theoretically,similar to the standard LBM,the DBM has the outstanding merits of simplicity for programming and high parallel efficiency,because the discrete Boltzmann equation is uniformly linear and all the information transfer in DBM is local in time and space.However,the parallel efficiency of our DBM has never been demonstrated in a numerical way.To this end,we conduct simulations using parallel programming based on the Message-Passing Interface standard.Calculations are carried out on the supercomputer ARCHER.Table 1 exhibits the parallel efficiency.Eight tests are performed using the number of processing cores,Np=1×1,2×2,4×4,8×8,16×16,32×32,64×64,and 128×128,respectively.The mesh is chosen asNx×Ny=3200×3200.The other parameters are identical to those for Fig.4.After 8000 iterative steps,the running time ist1=755840,t2=198112,t3=55120,t4=13792,t5=3476,t6=881,t6=221,andt8=59 seconds,respectively.De fine the parallel efficiency asEp=Npti/t1,withi=1,2,...,6.Then the efficiency is 100%,95.4%,85.7%,85.6%,84.9%,83.8%,83.5%,and 82.0%for the eight tests,respectively.It is evident that the parallel efficiency of the DBM is quite high. Table 1 Parallel efficiency study of the DBM. Fig.2 Mole fractions YAin the binary diffusion at time instants:t=0.005,0.020,and 0.060,respectively.Symbols stand for DBM simulation results,and solid lines for the corresponding analytical solutions. To validate its capability of describing the interaction between two species,this DBM is used to simulate binary diffusion.Initially,the mole concentration is described by the following step function,(nA,nB)L=(0.9,0.1)and(nA,nB)R=(0.1,0.9),where the suffixesLandRindex the left and right parts,respectively.The temperature isT=1,the velocityu=0,the molecular massmσ=1,the relaxation timeτ=10?3,the temporal step ?t=10?5,the spatial step ?x= ?y=5×10?4,the mesh gridNx×Ny=100×1.Figure 2 displays the mole fraction of speciesAat three time instants.Symbols are for DBM results,and solid lines for the analytical solution where?Yσ=0.8 is the initial mole fraction difference,and andχ=10?3the diffusion coefficient.We can find a satisfying agreement between the two sets of results. In this section,let us focus on the KHI.The initial field configuration is delineated in Fig.3.The left part is occupied by speciesAwith an upward velocityuL=uLeyand a mole concentrationthe right part is full ofBwith a downward velocityuR=?uReyand a mole concentrationBetween them is a perturbed interface with a transition layer.Mathematically, whereDρ(Du)represents the width of density(velocity)transition layer,x0denotes the averagedxposition of the cosine-shaped interface,Wandkare the perturbation amplitude and wave number,respectively.The pressurepis equal at the two sides of the interface.The two species have an identical velocity and temperature at the same location.The length and width of the physical domain areLx=1.5 andLy=0.5,respectively.The parameters are chosen asuR=0.5,Dρ=Du=Lx/300,W=Lx/200,x0=Lx/2,k=2π/Ly.Furthermore,boundary conditions are as follows:the inflow/outflow(zero gradient)boundary conditions in thexdirection,the periodic boundary conditions in theydirection.In addition,all quantities are expressed in nondimensional forms,i.e.,the widely accepted LB units,[27]in this work. Fig.3 Field configuration. Grid convergence is one of the most important issues in numerical simulations.To verify the validity of the simulation,a grid convergence test is firstly carried out using various grids:Nx×Ny=750×250,1500×500,3000×1000,and 6000×2000,respectively.The time step is?t=2.5×10?5,the relaxation timeτ=2×10?4,the molar massmA=3,andmB=1.Figure 4 delineates the molar fractionYA(=nA/n)along the liney=Ly/2 at the timet=1.As one can see,with increasing mesh grids,the numerical errors become smaller and smaller.The differences between simulations with grids 6000×2000 and 3000×1000 are small enough.Taking account of both accuracy and efficiency,we carry out this simulation on the gird 3000×1000. Fig.4 Grid convergence test:molar fraction of species A along the line y=Ly/2 at the time t=1.The solid,dashed,dotted,and dot-dashed lines denote the mesh grids Nx×Ny=6000×2000,3000×1000,1500×500,and 750×250,respectively.The inset enlarges the outlined rectangular region. Fig.5 Contours of physical quantities at time instants t=0.5,1.0,2.0,and 3.0,respectively.The leftmost,middle,and rightmost columns show the snapshots of the molar fraction of A,pressure,and vorticity,respectively. Figure 5 depicts the molar fractionYA,pressurep(=nT),and vorticityω(=?xuy??yux)at time instantst=0.5,1.0,2.0,and 3.0,respectively.It is evident that the perturbed interface begins to wiggle due to the velocity shear att=0.5.After the initial linear growth stage,a rolled-up vortex emerges around the interface att=1.0.Then,att=2.0,a larger vortex is observed in the snapshot.Att=3.0,the thickening interfacial layer indicates that KHI promotes the mixing and penetrating of the miscible fluid components.Comparing pressure contours with vorticity,we can find that the minimum pressure is located at the vortex center,and the maximum pressure is at the position where two opposite direction flows encounter each other.The flow field varies with space and time.In fact,the pressure gradient offers the centripetal force required by the rotating flows.Moreover,the interface is continuous and smooth,as shown in Fig.5.The coherent structures demonstrate that the DBM has a good ability of capturing interface deformation. As an initial application,we preliminarily study two kinds of nonequilibrium e ff ects,andin the evolution of KHI.To give an intuitive impression,Fig.6 depicts the contours of them at the momentt=2.0.The values ofare greater than zero around the vortex where the shear is significant,while they are close to zero far away from the interface where the velocity di ff erence is low.Meanwhile,values ofare large at the contact between the two media,while they approach zero where the interaction between the fluids is weak. Fig.6 Contours of nonequilibrium quantities, and at the moment t=2.0. Fig.7 Evolution of nonequilibrium quantities with various relaxation times: τ1=10?∫∫4(squares), τ2=2×10?4(diamonds),τ3=4×10?4(circles),and τ4=8×10?4(triangles),respectively.(a) dxdy.(b) To investigate the influence of relaxation time on the nonequilibrium KHI,we conduct four runs with various relaxation times,τ1=10?4,τ2=2×10?4,τ3=4×10?4andτ4=8×10?4,respectively.Let us de fine the Reynolds number aswhere the characteristic density isthe characteristic velocity(uL+uR)/2,the characteristic lengththe dynamic viscosityCorrespondingly,Re=3750,1875,937.5,and 468.75,for the four runs,respectively.Taking into account of both numerical accuracy and computational efficiency,we chose the spatial step as?x=?y=2.5×10?4,5×10?4,10?3,and 2×10?3,respectively.And the temporal step is?t=1.25×10?5,2.5×10?5,5×10?5,and 10?4,respectively. Figure 7 plots the evolution of nonequilibrium quantitiesxdyandrespectively,where the integral is extended over all physical spaceLx×Ly.Actually,dxdyanddxdyindicate the global nonequilibrium effect(GNE)of speciesσin the physical region from two different points of view.dxdystands for the global strength of the viscous stress,whiledxdyrepresents the global intensity of the heat flux.The lines with squares,diamonds,circles,and triangles stand for the relaxation timesτ1,τ2,τ3,andτ4,respectively.It is evident that the GNEs become stronger for larger relaxation times.The evolution of GNE shows firstly increasing then decreasing trends.dxdyanddxdydo not reach their peaks simultaneously,anddxdyreaches the maximum earlier thanPhysically,there are competitive mechanisms in the evolution of GNEs.The GNE is associated with the local nonequilibrium effect and the nonequilibrium area.On the one hand,the interface is lengthened with the development of the vortex.The increasing interface enhances the GNEs.On the other hand,the interface is widened in the process of the binary diffusion and thermal conductivity,hence the physical gradients become smooth.The reducing physical gradients weaken the local nonequilibrium effects. In thermodynamics,entropy of mixing is part of the increasing entropy when separate systems with different components contact and mix,before the establishment of a thermodynamic equilibrium state.The statistical concept of randomness is utilized for statistical mechanical explanation of the entropy of mixing.Mathematically,the entropy of mixing per unit volume takes the form, whereYσis the molar fraction of speciesσ.The entropy of mixing is a typical thermodynamic nonequilibrium variable.It indicates the mixing extent and nonequilibrium process in various miscible fluid systems. Fig.8 Contours of the entropy of mixing at time instants t=0.5,1.0,2.0,and 3.0,respectively.The four columns,from left to right,correspond to the relaxation times τ1=10?4,τ2=2 × 10?4,τ3=4 × 10?4,and τ4=8×10?4,respectively. Figure 8 illustrates the snapshots of entropy of mixing in the evolution of KHI.The four columns,from left to right,correspond to cases with relaxation timesτ1,τ2,τ3,andτ4,respectively.The four rows,from top to bottom,correspond to the time instantst=0.5,1.0,2.0,and 3.0,respectively.It is clear in each column that the mixing area increases in the evolution of KHI.The rolled-up vortex lengthens the interface and promotes the mixing process.Meanwhile,it can be found in every row that the mixing area is larger for a larger relaxation time,because the diffusion coefficient,which enhances the mixing process is proportional to the relaxation time.[36] For the purpose of a quantitative study,we probe the temporal evolution of entropy of mixing with various relaxation times.Figure 9(a)shows∫∫SMdxdy,where the integral is extended over all physical region,and Fig.9(b)plots its growth rate.Obviously,in Fig.9(a),the entropy of mixing is higher for a larger relaxation time,which is consistent with Fig.8.Moreover,it is interesting to see in Fig.9(b)that the evolution of its growth rate shows three trends,i.e.,firstly reducing,then increasing,and f inally decreasing trends.Physically,there are competitive mechanisms in the evolution of the entropy of mixing.(i)The binary diffusion is fast when the gradient of molar fraction is sharp.The transition layer of the initial interface is relatively narrow,hence the diffusion and mixing is relatively fast.The mixing rate reduces with the increasing width of the transition layer in the early stage.(ii)The mixing process is promoted by the increasing length of material interface with the development of the vortex.In the evolution of KHI,the interface becomes longer and longer,hence the mixing rate increases in the second stage.(iii)With the ongoing diffusion,the material interface becomes wide and the gradients are smoothed.The mixing rate reduces and begins to approach zero,when the gradient becomes smaller and smaller around the vortex,in the final stage.It is of interest to find that the fast diffusion promotes the mixing process directly and initially,but slows the mixing rate indirectly and finally,in the dynamic process of KHI. Fig.9 Evolution of entropy of mixing and its growth rate with various relaxation times: τ1=10?4(squares),τ2=2 ×10?4(diamonds),τ3=4× 10?4(circles),and τ4=8 ×10?4(triangles),respectively. In thermodynamics,free enthalpy of mixing is another interesting thermodynamic nonequilibrium variable.Let us introduce Gibbs free enthalpy of mixing per unit volume as below, Note thatHM≤0 since 0≤Yσ≤1 and lnYσ≤0.In other words,free enthalpy of mixing is always nonpositive,and it is opposite to entropy of mixing that is nonnegative.Mathematically,HM=?SMT. Figure 10 depicts the fields of free enthalpy of mixing and temperature at time instantst=0.5,1.0,2.0,and 3.0,respectively.The case corresponds to the first column in Fig.8 with the relaxation timeτ1=10?4.In order to make a clear comparison to the entropy of mixing,the minus free enthalpy of mixing is shown.Since the free enthalpy of mixing is the function of the entropy of mixing and temperature,the contours of temperature are plotted aside.A comparison between Figs.8 and 10 gives two points.On the one hand,the entropy of mixing and minus free enthalpy of mixing exhibit similar contours,as both of them are located at the interface between the two species.On the other hand,the entropy of mixing and minus free enthalpy of mixing show some different values due to the spatio-temporal variation of temperature in the evolution of KHI. Fig.10 Contours of minus free enthalpy of mixing(?HM)and temperature(T)with the relaxation time τ=10?4at time instants t=0.5,1.0,2.0,and 3.0,respectively. Fig.11 Evolution of the free enthalpy of mixing and its growth rate with various relaxation times: τ1=10?4(squares),τ2=2× 10?4(diamonds),τ3=4 ×10?4(circles),and τ4=8× 10?4(triangles),respectively. Atwood number is an important parameter that affects the growth of KH instability.It is defined as withρσ=nσmσandnσ=1 in this section.Let us consider four cases,i.e.,mA=1,2,3,and 4,with fixedmB=1.The corresponding Atwood numbers are At1=0,At2=1/3,At3=1/2,and At4=3/5,respectively.The other parameters are the same as those in Fig.5. Figure 12 depicts the snapshots of the molar fractionYA,the speedand the temperatureTat timet=1 with various Atwood numbers.We can find an upward movement in the vortex center with the increasing Atwood numbers.Physically,the average flow velocity in theydirection,uy,is zero around the interface for the casemA=mB,and it increases with the increasing mass ratio of speciesAtoB,i.e.,Rm=mA:mB.Hence the vortex goes up as the flow speeduyincreases with the increasing Atwood numbers.Moreover,it is clear in the first column that the vortex becomes wider in thexdirection for a smaller Atwood number.The second column shows that the maximum flow speed increases with the increasing Atwood number.It can be obtained from the first and second columns that the light mediumBhas larger speed than the heavy oneAaround the vortex.Finally,the third column shows that,with the increasing Atwood number,the maximum temperature increases and the minimum temperature reduces.It is seen from the first and third columns that the minimum temperature is located at the vortex center,while the maximum temperature is located at the interface where the conversion from the shear kinetic energy to the internal energy is intense.In sum,the vortex has a smaller area,the light medium has faster speed,and the temperature has sharper gradients for a larger Atwood number. Fig.12 Contours of physical quantities at time t=1.The leftmost,middle,and rightmost most columns are for the molar fraction of A,flow speed,and temperature,respectively.The four rows from top to bottom correspond to Atwood numbers At1=0,At2=1/3,At3=1/2,and At4=3/5,respectively. Figure 13 exhibits the evolution of nonequilibrium quantities with various Atwood numbers.Figure 13(a)shows that,for speciesA,the global strength of viscous stress,dxdy,is smaller for a larger Atwood number.On the contrary,for speciesB,the global strength of the viscous stress,dxdy,increases with the increasing Atwood number,as shown in Fig.13(b).Physically,with the increasing mass ratio of speciesAtoB,the flow velocity of the heavy mediumAhas a relatively small change,while the flow velocity of the light oneBhas a relatively large change,during an interval.In addition,Fig.13(c)shows that the global intensity of the heat flux,dxdy,decreases with the increasing Atwood number.While in Fig.13(d),the peak of the global intensity of the heat flux,dxdy,is similarly high for different Atwood numbers.Because,mathematically,is roughly inversely proportional tomσ.[32]Furthermore,for a larger Atwood number,the peaks of eitherdxdyordxdyemerge later,because the amplitude of the perturbed interface grows more slowly.[6] Fig.13 Evolution of nonequilibrium quantities with various Atwood numbers:At1=0(squares),At2=1/3(diamonds),At3=1/2(circles),and At4=3/5(triangles),respectively.(a) dxdy,(b) dxdy, Fig.14 (a)Entropy of mixing and(b)its growth rate,(c)free enthalpy of mixing and(d)its growth rate,with the Atwood number:At1=0(squares),At2=1/3(diamonds),At3=1/2(circles),and At4=3/5(triangles),respectively. Figure 14 illustrates the evolution of entropy of mixing,free enthalpy of mixing,and their growth rates with the Atwood number:At1=0(squares),At2=1/3(diamonds),At3=1/2(circles),and At4=3/5(triangles),respectively.It is evident in Fig.14(a)that the entropy of mixing is lower for a larger Atwood number.Figure 14(b)shows that,for each Atwood number,the growth rate of entropy of mixing has three trends,i.e., firstly reducing,then increasing,and finally decreasing trends.In contrast,as shown in Figs.14(c)and 14(d),the free enthalpy of mixing is higher for a larger Atwood number,and its growth rate shows firstly increasing,then reducing,and finally increasing trends.The trough(peak)in Fig.14(b)and the peak(trough)in Fig.14(d)take place almost simultaneously.Both the trough and peak emerge earlier for a smaller Atwood number in either Fig.14(b)or Fig.14(d).Because the growth rate of the perturbed interface is higher and the mixing area is wider for a smaller Atwood number,as shown in Fig.12. As a mesoscopic kinetic method,the discrete Boltzmann method(DBM)not only recovers the traditional NS equations in the continuum limit,but also gives various nonequilibrium information.Besides,the discrete Boltzmann equations are in a uniform linear form,which are easy to code with high parallel efficiency.In this work,we adopt the DBM to investigate the nonequilibrium process of Kelvin-Helmholtz instability(KHI).First of all,two kinds of nonequilibrium manifestations,i.e.,the viscous stresses and heat fluxes,are preliminarily studied.It is found that the global intensities of viscous stresses and heat fluxes become stronger for a larger relaxation time,and they firstly increase then decrease in the KHI process.Physically,the increasing nonequilibrium area enhances the GNEs,while the reducing physical gradients weaken the nonequilibrium effects. In addition,the entropy of mixing is higher for a larger relaxation time,and its growth rate shows firstly reducing,then increasing,and finally decreasing trends in the KHI process.On the contrary,the free enthalpy of mixing is lower for a larger relaxation time,and its growth rate has firstly increasing,then decreasing,and finally increasing trends.Physically,there are competitive mechanisms.(i)The binary diffusion is fast when the gradient of molar fraction is sharp.The mixing rate reduces with the increasing width of the transition layer in the early stage.(ii)The mixing process is promoted by the increasing length of material interface in the second stage.(iii)As physical gradients are smoothed due to the binary diffusion,the mixing speed reduces and begins to approach zero in the final stage.It is of interest to find that the diffusion promotes the mixing process directly and initially,but hinders the mixing rate indirectly and eventually. Moreover,we study the influence of Atwood number on the growth of the nonequilibrium KHI.With the increasing Atwood number,the global strength of viscous stress on the heavy medium reduces,while the one on the light medium increases.Physically,with the increasing mass ratio,the heavy medium has a relatively small velocity change,while the light one has a relatively large velocity change,in the dynamic process.Since the heat flux is roughly inversely proportional to the molar mass,the global intensity of the heat flux reduces with the increasing molar mass.Furthermore,the growth rate of the perturbed interface increases with the decreasing Atwood number.Consequently,for a smaller Atwood number,the peaks of nonequilibrium manifestations emerge earlier,and the entropy of mixing and free enthalpy of mixing change faster.
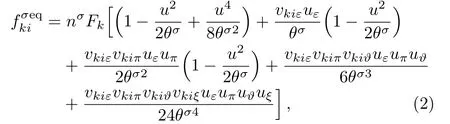
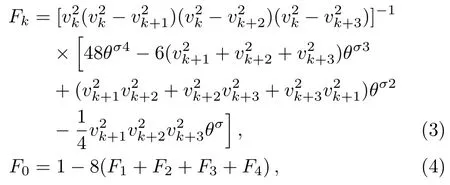
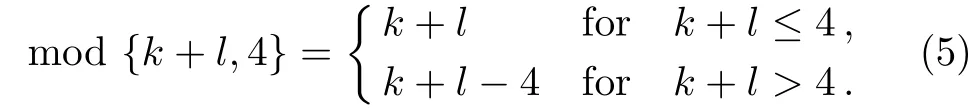
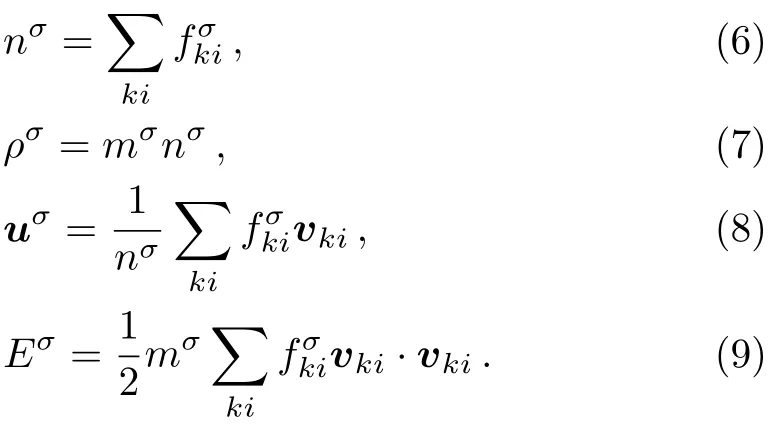
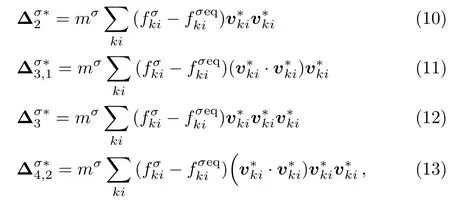
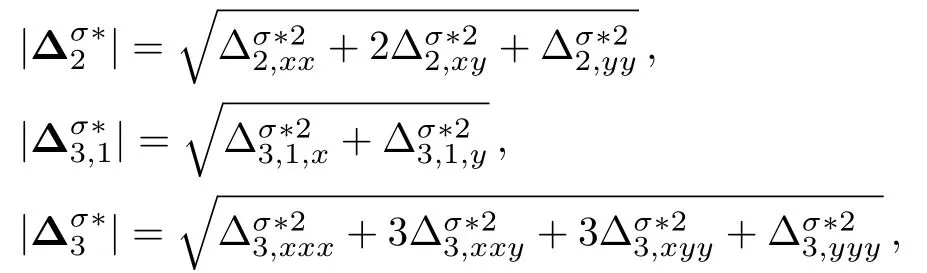



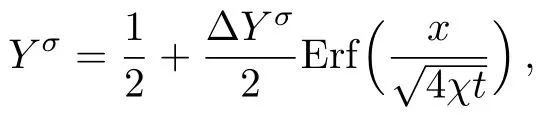
3 Simulation and Investigation
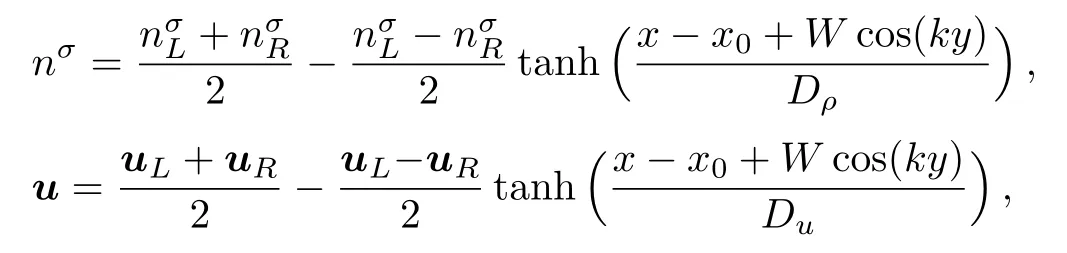
3.1 Grid Convergence Test

3.2 Nonequilibrium Effects

3.3 Entropy of Mixing

3.4 Free Enthalpy of Mixing
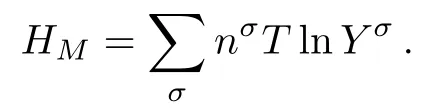
3.5 Atwood Number


4 Conclusions and Discussions
 Communications in Theoretical Physics2019年1期
Communications in Theoretical Physics2019年1期
- Communications in Theoretical Physics的其它文章
- Nontrivial Effect of Time-Varying Migration on the Three Species Prey-Predator System?
- A One-Dimensional Discrete Boltzmann Model for Detonation and an Abnormal Detonation Phenomenon?
- Impact of Colored Noise on Population Model with Allee Effect?
- Improved Five-Parameter Exponential-Type Potential Energy Model for Diatomic Molecules?
- Dynamically Tunable and High-Contrast Graphene-Based Terahertz Electro-Optic Modulator?
- Multipolar Structure of Equilibrium Shear Flow Field in Toroidal Plasmas?
