Ying-Ke Lei (雷瑩珂) and Chun Liu (劉純)

CAS Key Laboratory of Theoretical Physics, Institute of Theoretical Physics, Chinese Academy of Sciences,Beijing 100190, China

School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China

(Received January 2, 2019; revised manuscript received January 19, 2019)

Abstract CP violation in the lepton sector, and other aspects of neutrino physics, are studied within a high scale supersymmetry model.In addition to the sneutrino vacuum expectation values(VEVs),the heavy vector-like triplet also contributes to neutrino masses.Phases of the VEVs of relevant fields, complex couplings, and Zino mass are considered.The approximate degeneracy of neutrino masses mν1 and mν2 can be naturally understood.The neutrino masses are then normal ordered, ～0.020 eV, 0.022 eV, and 0.054 eV.Large CP violation in neutrino oscillations is favored.The effective Majorana mass of the electron neutrino is about 0.02 eV.

Key words: fermion mass hierarchies, neutrino oscillation, CP violation charged lepton

1 Introduction

Neutrino physics, like leptonic CP violation, is an interesting topic[1]in the current research of particle physics.Among other things, it might be the final place where experiments of particle physics will give definite results in the near future.The results will check various theoretical models about the fermion masses of the Standard Model(SM).

We proposed that supersymmetry (SUSY)[2]can be the theory underlying the fermion masses in Refs.[3–5].The basic idea is the following.It assumes a flavor symmetry.The flavor symmetry is broken after the sneutrinos obtain nonvanishing vacuum expectation values (VEVs).(In this way, SUSY is motivated.)These VEVs result in a nonvanishing neutrino mass.The empirical smallness of neutrino masses needs very large SM super partner masses to be understood which are about 1012GeV.Thus, our SUSY is of high scale breaking.[6?8]

A further natural assumption is that the flavor symmetry breaks softly.Namely the soft SUSY breaking masses of the sfermions do not obey the flavor symmetry either.The theoretical reason is that the soft masses are due to the supergravity effect which generically breaks any global symmetry.Soft breaking of the flavor symmetry implies that the lepton number violation due to sneutrino VEVs is explicit instead of being spontaneous.Therefore there is no any massless Nambu-Goldstone boson related to nonvanishing sneutrino VEVs.Actually the large masses of the model make the low energy effective theory just the SM via Higgs mass fine tuning,except for that we have an understanding of the hierarchical pattern of the charged lepton masses, or that of the SM Yukawa coupling constants.

Let us briefly review the model in a simple way.The SM is SUSY generalized.The flavor symmetry isZ3cyclic among the three generation SU(2)Llepton doubletsL1,L2andL3.The other fields are trivial underZ3.TheZ3invariant combinations areand?αβ(Lα1Lβ2+Lα2Lβ3+Lα3Lβ1)withαandβdenoting the SU(2)Lindices.In terms of the following redefined lepton superfields,the aboveZ3invariant combinations areLτand?αβLαe Lβμ, respectively.The superpotential is then

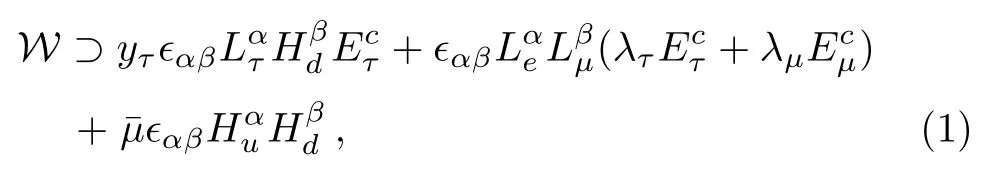
whereHuandHdare the two Higgs doublets, the righthanded lepton singletEcτis defined as the one which couples toLτ, andEcμis that orthogonal toEcτand with a coupling toLeLμ.yτ,λτandλμare coupling constants.(Note that considering the mixing betweenLτandHdgives the same form of the above superpotential.[4])It is seen that the electron is massless, becauseEceis always absent in the Lagrangian.This is true whenever SUSY is conserved,the nonvanishing electron mass is due to SUSY breaking (together with electroweak gauge symmetry and flavor symmetry breaking via loops).Note that all the coupling constants in our superpotential are assumed to be natural values, say typically～0.01-1, and the mass parameteris taken to be large～1012GeV.The SM fermion mass hierarchy is due to symmetries and their breaking.

In addition, a heavy vector-like SU(2)Ltriplet fieldT()with hypercharge 2(?2)needs to be introduced so as to make the Higgs mass realistic.[5?6]This triplet field also contributes to neutrino masses.In terms of the redefined fields, the flavor symmetric superpotential relevant to the tripletTandfields is

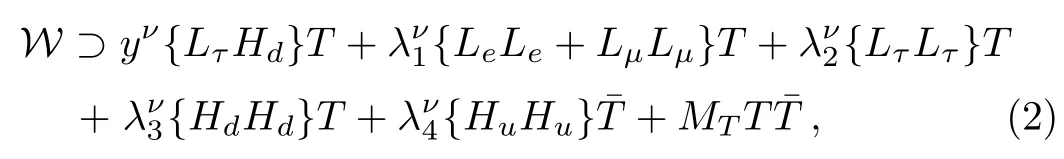
withMTthe mass～1013GeV.The braces denote that the two doublets form an SU(2)Ltriplet representation.

The soft SUSY breaking terms in the Lagrangian are in general form, which also break the flavor symmetry.[3?5]All the mass parameters of the model are taken to be about (1012–1013)GeV.The spontaneous gauge symmetry breaking of the SM occurs.Through fine tuning, the right electroweak vacuum is obtained.By including contribution due to the triplet field, this model can give reasonable neutrino spectrum and the mixing pattern, and predicted the right order ofθ13.[4?5](The quark sector was considered in Ref.[4].)

Roughly speaking about the electroweak symmetry breaking.There are five scalar doublets, the mass parameters are all large～1012GeV.Eigenvalues of their mass-squared matrix are generically large.However, one of these values can be exceptional,because it is a difference between two large parameters.It is this difference that makes the fine-tuning possible.Whence the difference is tuned to be about?(100 GeV)2,correct electroweak symmetry breaking occurs.The corresponding eigenstate field is one superposition of the five doublets.It is the only light scalar doublet, and is just the SM Higgs field from the point of view of the low energy effective field theory.The SM Higgs gets a VEV is equivalent to that the original two Higgses and sleptons get their VEVs.[4?5]

2 Complex Couplings and Sneutrino VEVs

In this paper, we will carefully consider CP violation of the lepton sector, and completely analyze the neutrino masses and mixing.In general,the coupling constants are complex, however, because of the flavor symmetry, many of them can be made real via field phase rotation.In the superpotential Eq.(1)for charged leptons, all the couplings can be adjusted to be real.On the other hand, in the superpotential Eq.(2)for neutrino masses, the couplings cannot be all taken real, as can be seen in the following way.The mass parametersandMTare taken real,thusHuandHdalways have opposite phases,and so doTand.λν2is real via rotating the phase ofLτ,λν4is real via rotatingHu(or),yτis real viaEcτ,λτreal viaLeLμrotating, andλμreal viaEcμ.In such a phase convention, onlyyν,λν1andλν3can be complex.Theλν1term will contribute to the neutrino masses, which was omitted in our previous analysis.[5]

In the soft SUSY breaking terms,the mass parameters and coupling constants are generally complex, and there is no enough freedom to rotate all of the phases away.

The scalar potential relevant to the electroweak symmetry breaking is

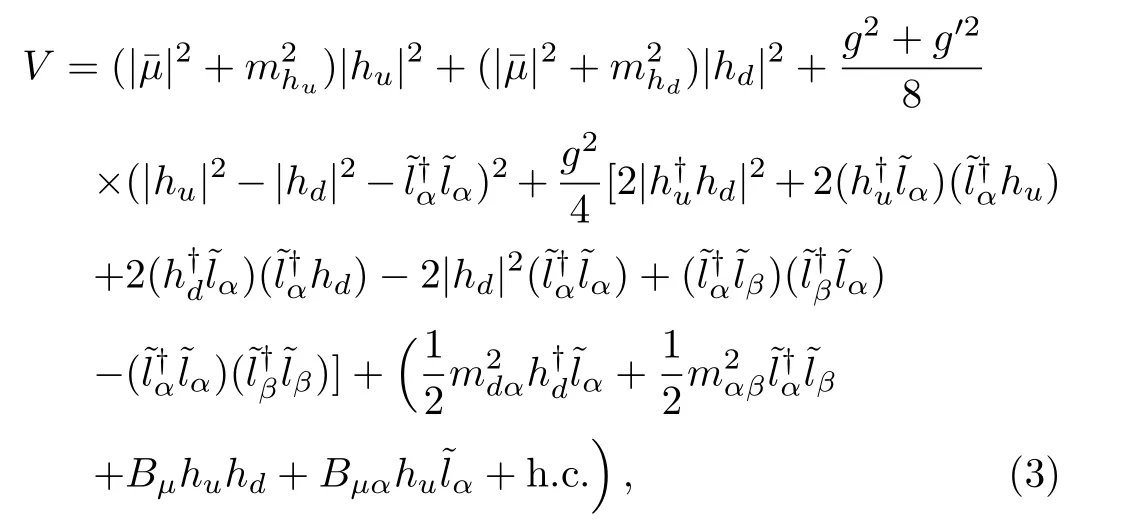
wheregandg′are SM gauge coupling constants.huandhddenote the scalar components ofHuandHd, respectively, and’s left-handed sleptons.m2h(u,d),m2dα,m2αβandBμ,Bμαare soft squared masses.

In considering CP violation of the scalar potential,the essential point lies in the soft bilinear terms where the mass parameters are complex.Field redefinition ofhdand ?lαmay remove phases ofBμandBμαrespectively, however,the phases ofm2dαand off-diagonal terms ofm2αβare still there.This means that after the electroweak symmetry breaking, Higgs and sneutrino VEVs are complex in general.(Previously we took all the VEVs real.)In the analysis, we still have the freedom to choose the VEV of Higgs fieldhuto be real, and VEVs of the Higgs and the sneutrino fields are denoted aswhere the phases have been explicitly written down.These VEVs enter the lepton mass matrices and thus contribute to CP violation in the leptonic mixing.

3 Neutrino Masses

The sneutrino VEVs result in a nonvanishing neutrino mass,

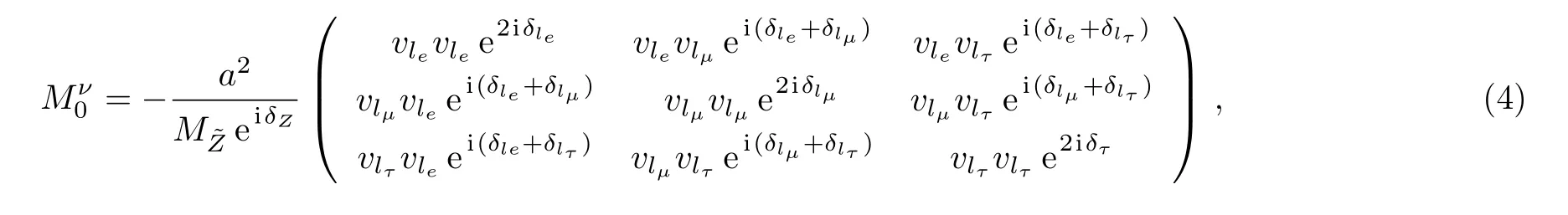
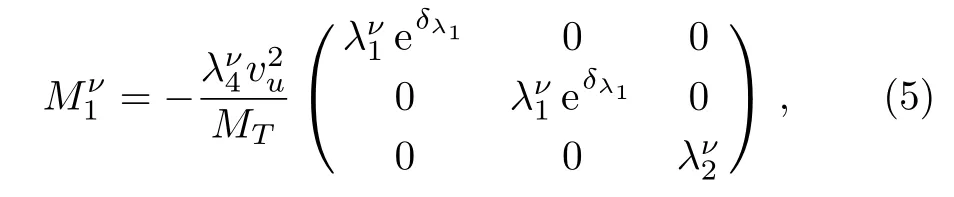
where the phase of couplingλν1has been explicitly written.This part of neutrino mass generation is realization of the type-II seesaw mechanism.[10]

The full neutrino mass matrix is

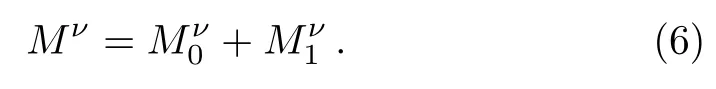
Note this is the full neutrino mass matrix of the model.It is due to tree level contribution of lepton number violation.The loop level contribution due to R-parity violation is negligible,[4]because the sparticles in the loops are very heavy.

The physics analysis includingλν1is different from our previous one.[5]We observe that it is natural to take thatMν1is numerically dominant overMν0, then there appears a degeneracy between the first two neutrinos.This roughly fits the neutrino spectrum obtained from neutrino oscillation experiments.This degeneracy is perturbed byMν0which also contributes neutrino mixing.Furthermore,it is interesting to note that inclusion ofλν1in certain cases does not really increase difficulty in the analysis becauseMν1is diagonal.

We rewriteMνby adjusting the diagonal partMν1to be proportional to identity matrix,

where

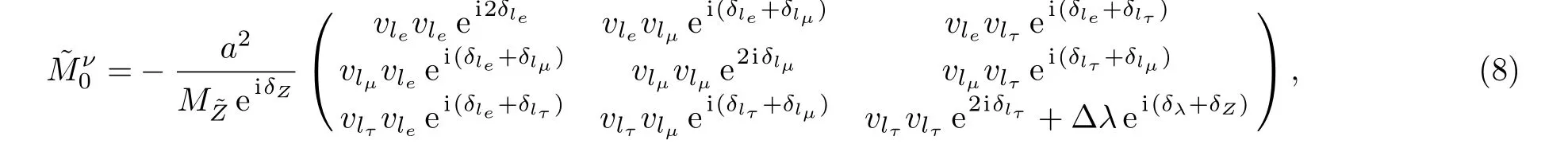
and

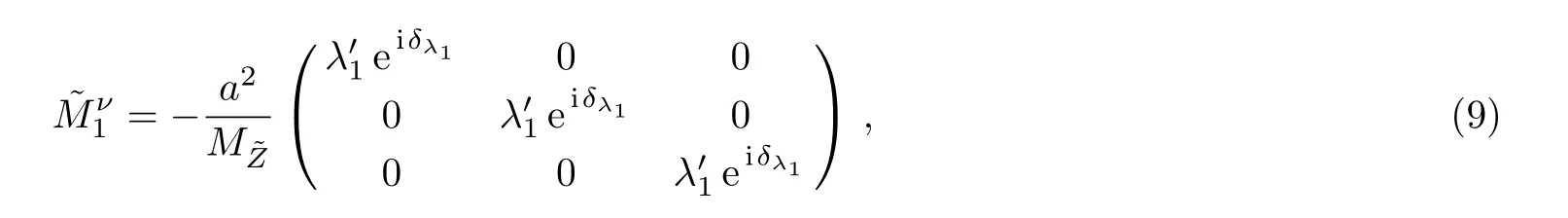
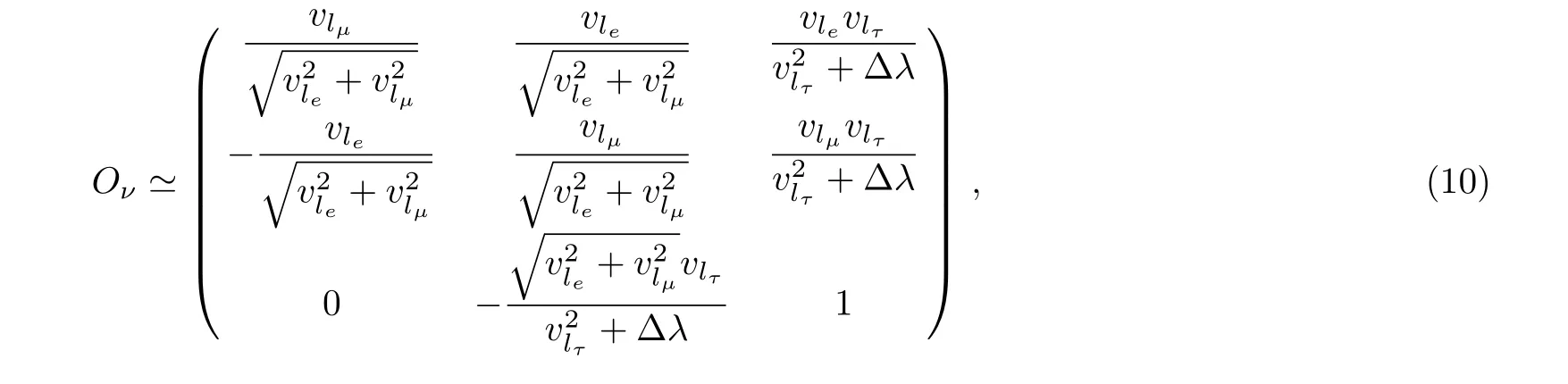
with eigenvalues

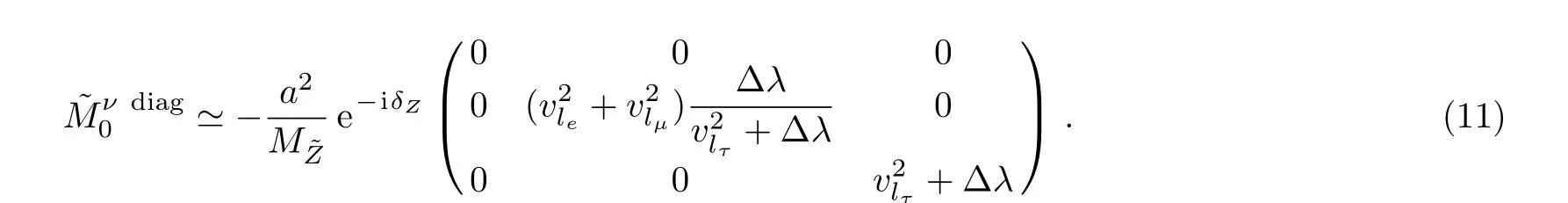
In fact,OνdiagonalizesMν,

Noticing that the diagonalized matrix is still complex, we further write that

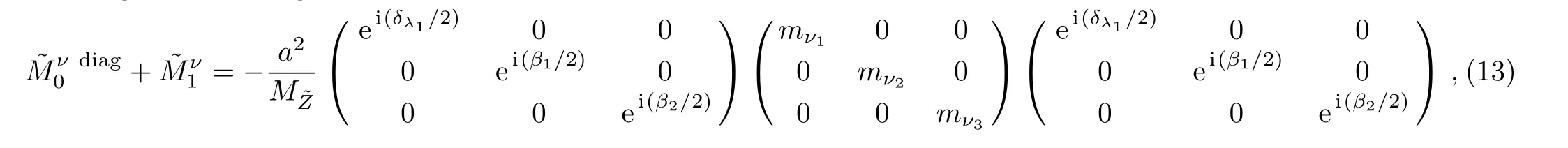
the neutrino masses in our model are

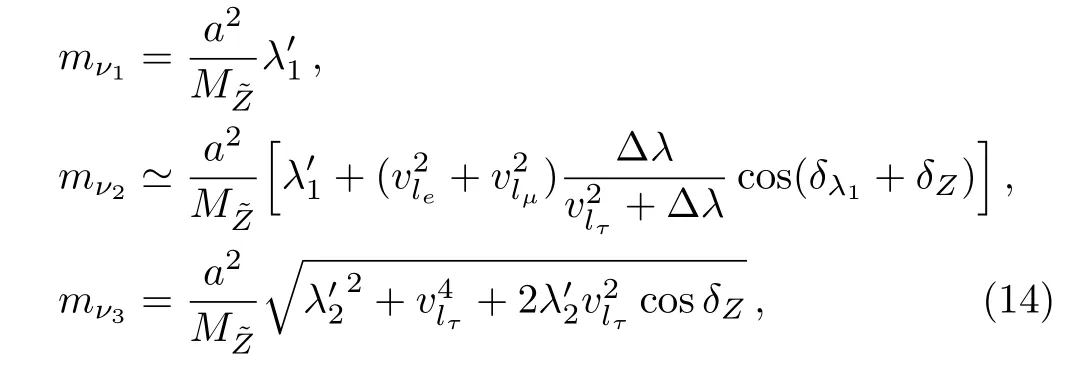
with the phases

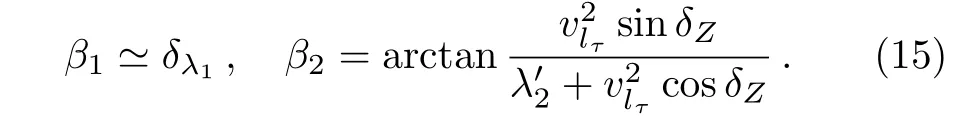
It is clear thatν1andν2are almost degenerate with a massTheir mass splitting is aboutv2lτ+ ?λand ?λhave the same order of magnitude by definition, and we take (v2le+v2lμ)?(λ′1/10).According to neutrino oscillation experiments,[12]?m212= 8.0×10?5eV2and|?m223|=2.4×10?3eV2, this model typically gives that

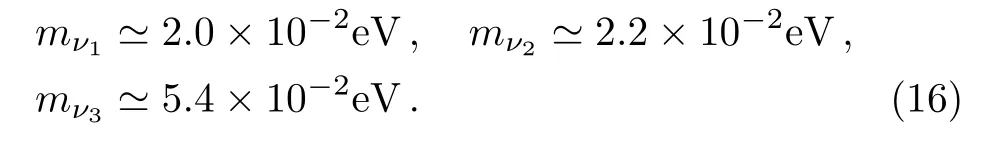
Naturally the phases in above formulae areO(1).This makes us to take all the cosines to beO(1)for simplicity in estimating the neutrino masses.Andmν3is numerically fixed by choosingλ′2andv2lτ.

Finally, we obtain the unitary matrixUνwhich diagonalizesMν,

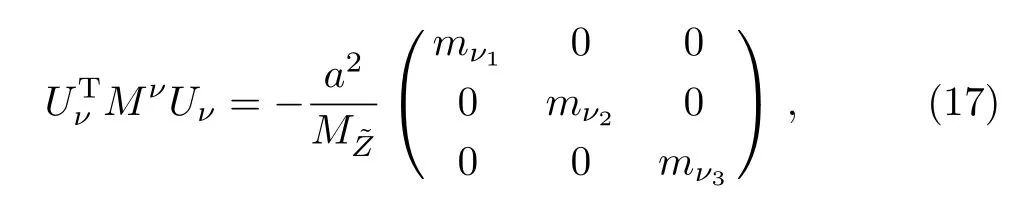
withPbeing the pure phase matrix appearing in Eq.(13).

4 Charged Lepton Masses

From Eq.(1), the charged lepton mass matrix is obtained.Considering the sneutrino and Higgs VEVs are complex, it is

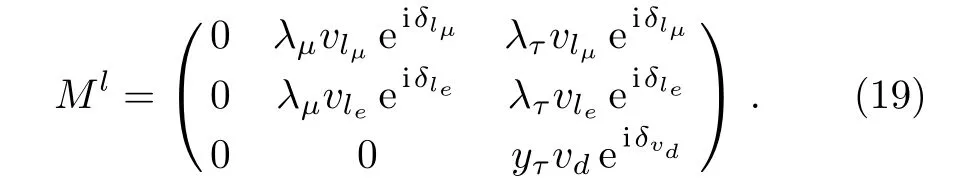
Here the electron mass is neglected.In this model, the electron mass would be a loop contribution of SUSY breaking terms,which also break the flavor symmetry and the electroweak symmetry.[3?4]The analytical expressions ofmτandmμare obtained as

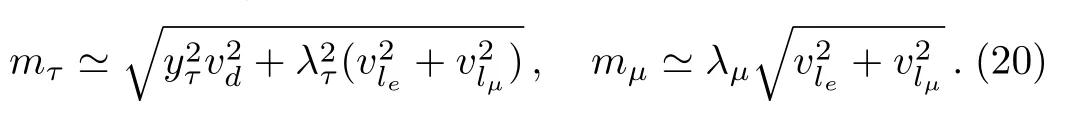
The mass matrixMlbasically fixes the mixing due to charged leptons with a precision ofme/mμ.It is standard to find the unitary matrixUlwhich diagonalizesMlMl?,

It can be expressed as

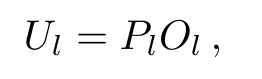
where

5 Lepton Mixing Matrix

Theνμ?ντmixing is

Theνe ?ντmixing is

Experimental data for best values of these mixings are|Ve2|?0.54,|Vμ3|?0.65, and|Ve3|?0.15.[12]Obviously,takingvlμ ?2vle,|Ve2|is in agreement with data.The value ofvlτis taken to be larger and still in the natural range,vlτ ?3vlμ.Choosing ?λ ?0.3v2lτ, it is easy to get|Ve3|?0.3|Ve2|.

For|Vμ3|, there are two terms in Eq.(25), neglecting the first term for simplicity,this mixing would be maximal ifnamelyλτ ?0.8.Of course, a smallerλτis more natural.That is to say,the atmospheric neutrino angle tends to be thatθ23<45?.However ifλτis larger,θ23>45?is also achievable.Therefore this model just slightly favors the atmospheric neutrino angle to be in the first octant.

The important CP violation in neutrino oscillations is given through the invariant parameterJ,[13]

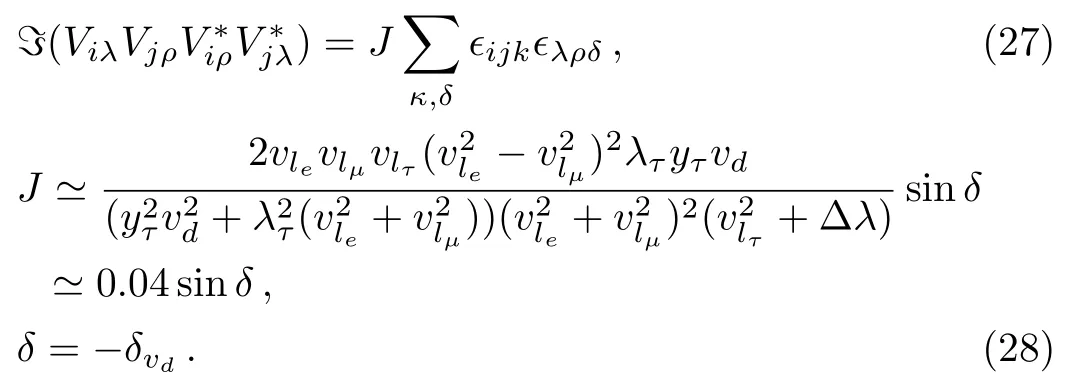
δvdis expected to be large, namely|sinδ| ～0.1–1.This agrees with current preliminary experimental results.[15]

6 Majorana Neutrino Mass

The effective Majorana mass in the neutrinoless double beta decay is

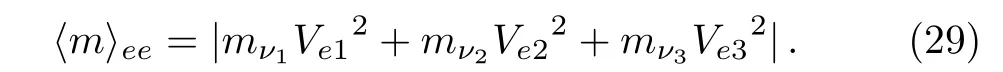
In this work, it is

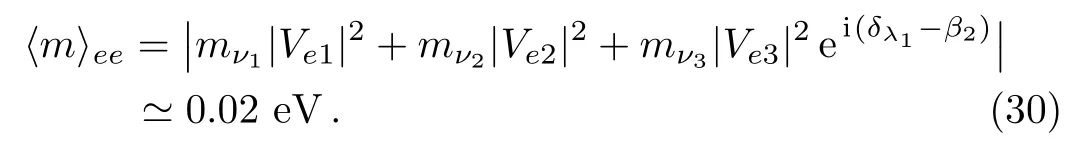
In the above formula, theVe3term has a Majorana phase dependence, which is negligibly small anyway.

7 Discussions

Like gauge theories which are used to describe the elementary particle interactions, SUSY is used for fermion masses.Our model is the minimal SUSY SM with a vector-like triplet field extension, but SUSY breaks at a high scale and the R-parity (lepton number)is not required.The sneutrino VEVs result in a neutrino mass,which is suppressed by the Zino mass.This is a nice realization of the type-I seesaw mechanism which, even does not need to introduce any right-handed neutrino.The triplet field is originally for the realistic Higgs mass.However, it also contributes to neutrino masses through a type-II seesaw mechanism.The Zino related seesaw mechanism results in only one massive neutrino.By including the triplet contribution,the neutrino masses can be realistic.Compared to our previous studies,[4?5]a more natural pattern for neutrino masses is obtained.

To be numerically natural, let us return back to the original superpotential in the beginning.The couplings are assumed to be taken natural values.The field VEVs are mainly fixed by the soft parameters in the Lagrangian,in addition to those in the superpotential.To fit the lepton spectrum and mixing, we takevle ?1 GeV,vlμ ?2 GeV,vlτ ?6 GeV,vd ?10 GeV,andvu ?228 GeV.Notevlτdoes not break the flavor symmetry, it is natural that its value is more close tovd.And the largevu/vdratio is for explaining the top quark mass.[4]Whenλ′1,λ′2andv2lτare in the same order, the correct neutrino spectrum is obtained.In terms of parameters in the superpotential,we haveM?Z ?3×1011GeV.MT ?(1–10)M?Z, andλ’s?(0.01–0.1).

It is necessary to check the reliability of our approximation in estimating the neutrino masses.That approximation about the phases can be good when the quantities appear in the mass formulae are hierarchical, say ifλ′1?v2le+v2lμ.As it has been seen that this is indeed the case formν2.Inmν3(Eq.(14)),λ′2,λ′1, andv2lτare of the same order.This allows us to look at an extreme case where the phase isπ.In this case, there is a possibility of inverted neutrino mass hierarchy, namely a very smallmν3.But this is achieved through a large cancellation betweenλ′2andv2lτ.Although this is possible, it is unnatural.

The physics of neutrinos in this work is quite different from that in Refs.[4–5].This is mainly due to the triplet.In Ref.[4], we introduced a singlet, the neutrino mass matrixMν1was that with only the 33 matrix element nonvanishing.And in Ref.[5], the triplet replaced the singlet for the Higgs mass in the beginning, however,in the neutrino mass analysis,we tookλν1to be zero which essentially was the same as that for the singlet case.Takingλν1to be zero was actually unreasonable because our principle is to treat all the basic couplings close to 0.01?1.As a result, in Refs.[4–5], there was always one massless neutrino.That led to that the Majorana mass﹤m﹥eeis about 10?3eV.In addition, in Ref.[5] it was wrong to say CP violation is small in the lepton sector.

8 Summary

In summary, in the model of high scale SUSY for understanding the fermion mass hierarchies, we have studied CP violation in the lepton sector,and other aspects of neutrino physics in detail.In the analysis, the phases of the Higgs and sneutrino VEVs,and contribution of theλν1term in superpotential(2),have been included.This analysis is more complete than previous consideration.The neutrino mass matrix, and the charged lepton one, are fixed by the model.Its specific feature is the triplet contribution,the approximate degeneracy of neutrinosν1andν2can be naturally explained.

This model could not predict exact values of the fermion masses because of the flavor symmetry breaking as well as SUSY breaking.However, the principle we follow is that all the coupling constants should be in the natural parameter range which is about (0.01–1).Taking triplet contribution dominant, and inputting relevant experimental data on leptons, we obtain that (i)mν1?0.020 eV,mν2?0.022 eV,mν3?0.054 eV.This normal ordering neutrino spectrum is to be checked in JUNO experiment.[14](ii)CP violation in neutrino oscillation most probably is large.There have been some experimental hint on this.[15]CP violation in neutrino oscillations is a great study task experimentally.[16](iii)The effective Majorana neutrino mass in the neutrinoless double beta decay is about 0.02 eV, it is within the detection ability of future measurements.[17](iv)θ23is only slightly favored being in the first octant.(v)The electron neutrino mass to be measured inβdecays is about 0.02 eV.This is,however, still one order of magnitude lower than the future limit of direct measurements.[18](vi)The sum of three neutrino masses is close to ∑mν ?0.1 eV.If the standard cosmology is correct, astrophysics measurements on the cosmic microwave background have constrained this sum to be<0.15 eV.[19]It is interesting to note that a recent analysis showed the sum is about～0.11 eV.[20]Most of the above predictions are close to their experimental limits, therefore, this model will soon be checked experimentally.

Acknowledgements

We would like to thank Gui-Jun Ding and Zhen-Hua Zhao for very helpful discussions.