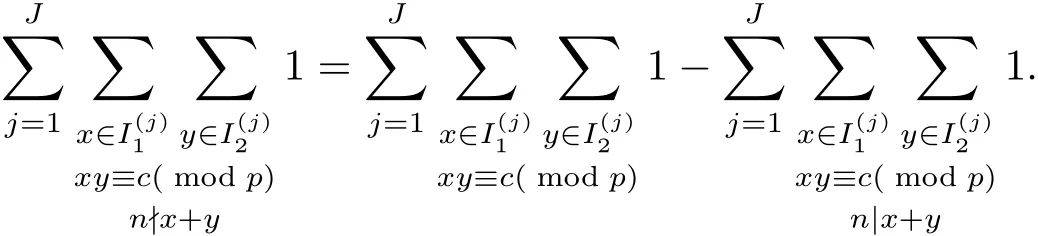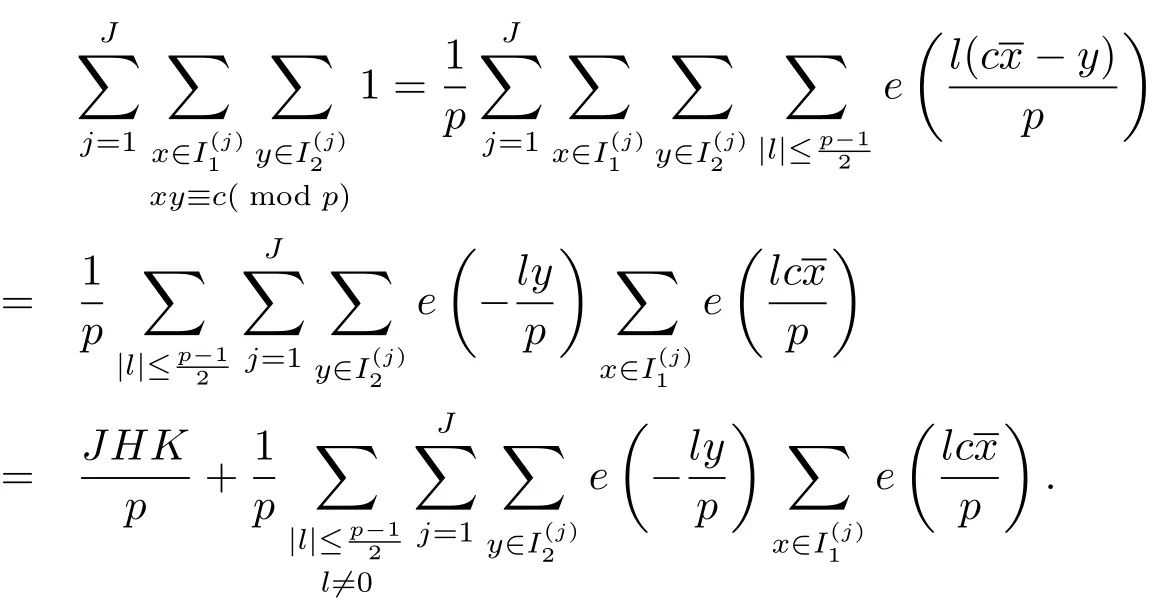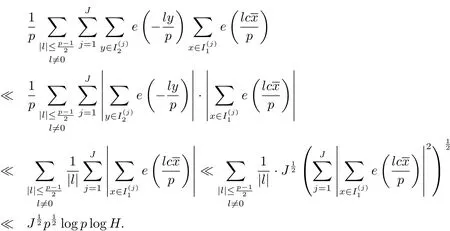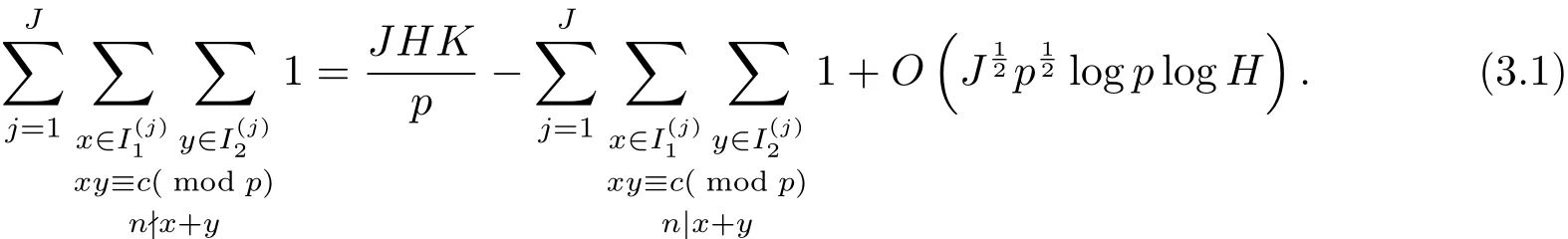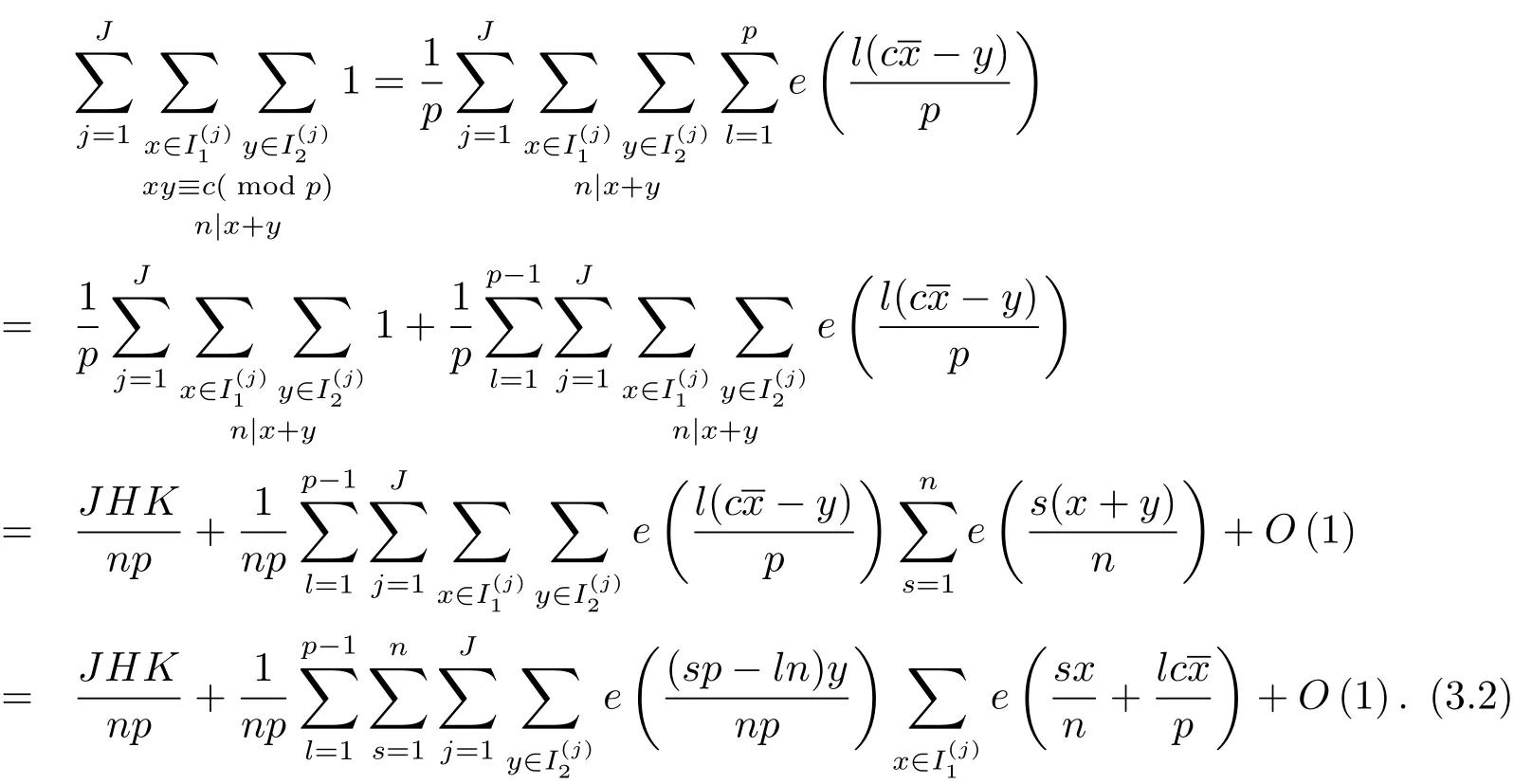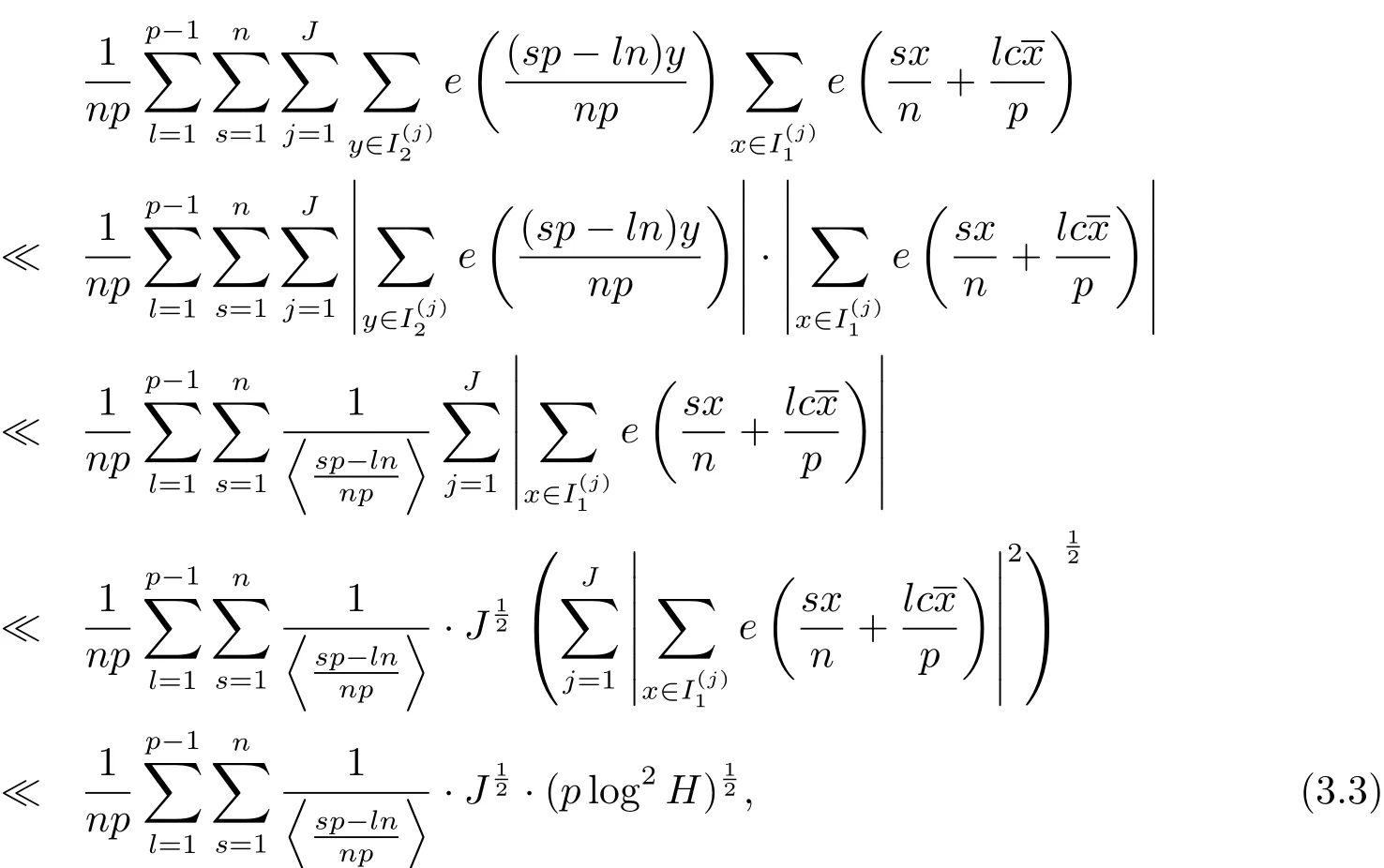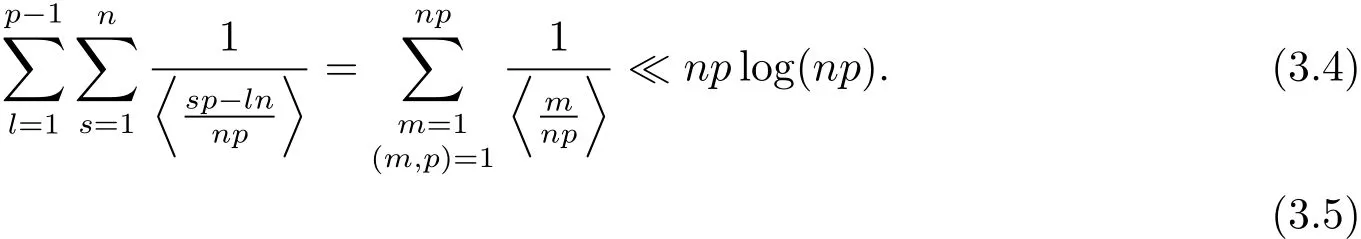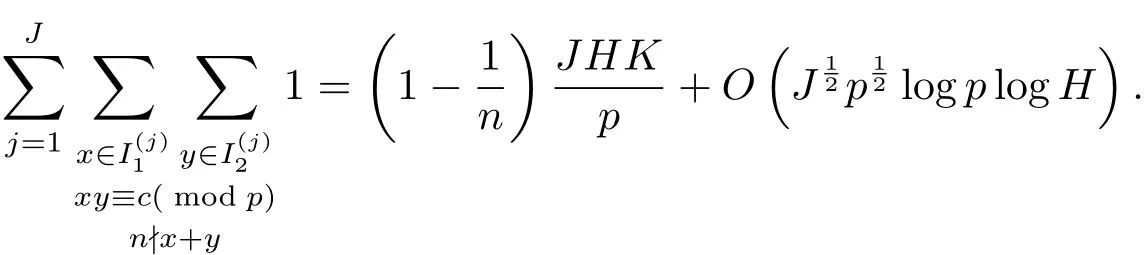關(guān)于短區(qū)間的并集中D.H.Lehmer問題的一個推廣
王曉瑛,曹艷梅
(西北大學(xué)數(shù)學(xué)學(xué)院,陜西西安 710127)
1 引言
設(shè)整數(shù)q>2.對任意與q互素的整數(shù)a,存在唯一的整數(shù)b滿足1≤b≤q以及ab≡1(mod q).D.H.Lehmer[1]建議研究a與b的奇偶性不同的情形.當(dāng)q=p為奇素數(shù)時,張文鵬[2]證明了
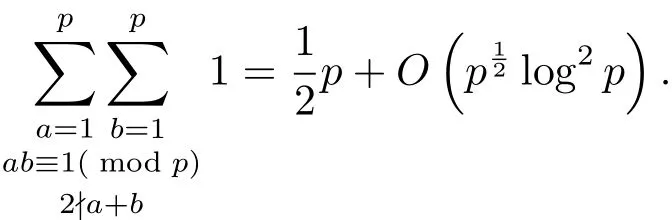
隨后在文獻[3,4]中,張文鵬還得到了漸近公式
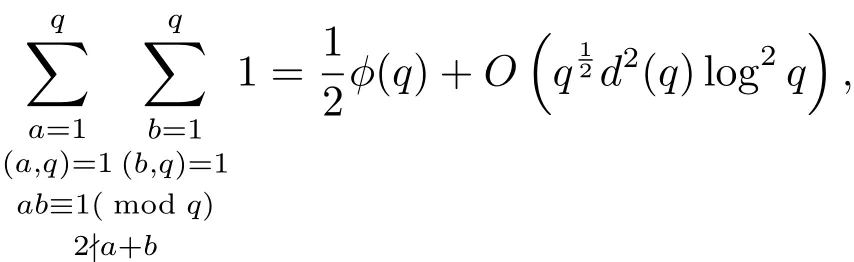
其中φ(q)為Euler函數(shù),d(q)是除數(shù)函數(shù).
設(shè)k為非負整數(shù).張文鵬[5]進一步證明了
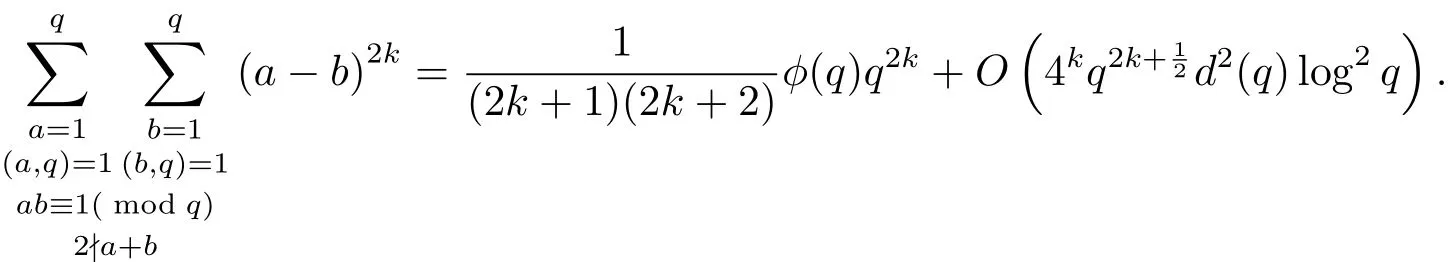
此外設(shè)0≤x,y≤1,文獻[5]中還得到了
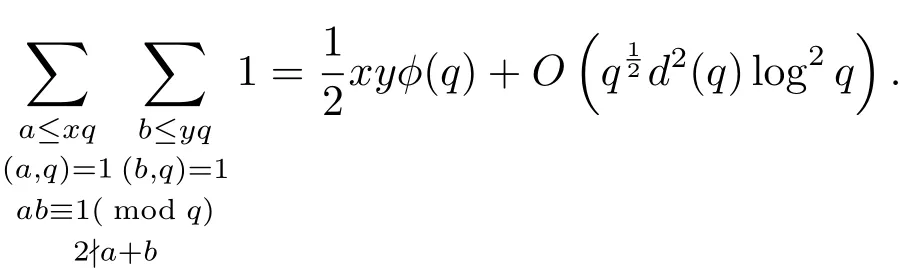
設(shè)實數(shù)l,δ滿足l≥0與0<δ≤1.王曉瑛與趙秋紅在文獻[6]中給出了漸近公式
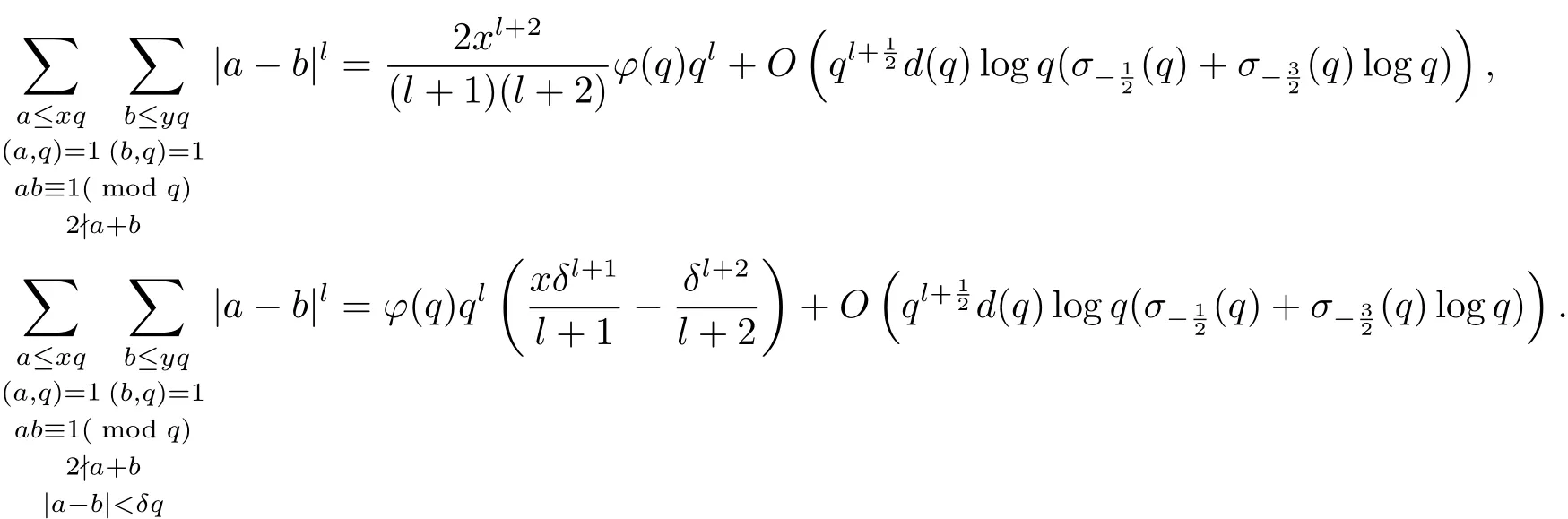
設(shè)q,c,n為整數(shù),滿足n≥2,q≥3以及(n,q)=(c,q)=1.設(shè) 0<δ1,δ2≤1.陸亞明與易媛[7]給出了D.H.Lemher問題的推廣
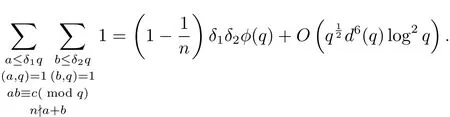
本文進一步考慮D.H.Lemher問題在短區(qū)間的并集上的推廣.主要結(jié)論如下.
定理1.1設(shè)p是奇素數(shù),H>0,K>0,并設(shè)是(0,p)的子區(qū)間,1≤j≤J,滿足當(dāng)j 6=k時.設(shè)c,n為整數(shù),滿足n≥2以及(n,p)=(c,p)=1.則有
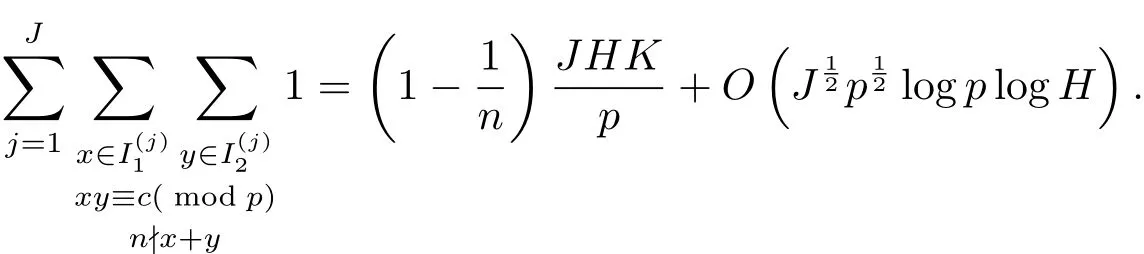
推論1.1當(dāng)時,存在j∈{1,2,···,J},使得方程xy≡c(mod p),n-(x+y)有解.
2 Kloosterman和的估計
設(shè)p>2為素數(shù),m與n為任意整數(shù).經(jīng)典的Kloosterman和的定義為
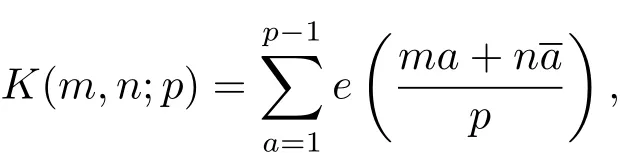
Browning和Haynes[9]給出了短區(qū)間的并集上的Kloosterman和的某種估計式.
引理 2.1設(shè) p是奇素數(shù),H 為正整數(shù),I1,···,IJ是(0,p)的互不相交的子區(qū)間,且對任意j滿足H/2<|Ij|≤H.設(shè)整數(shù)l與p互素,則有
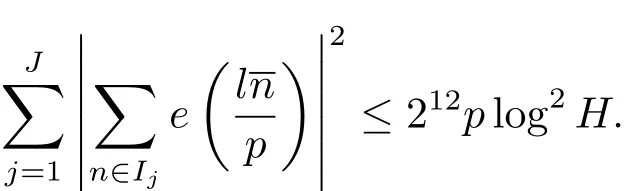
為了證明本文的定理,需要進一步考慮短區(qū)間的并集上的Kloosterman和的估計.
引理2.2設(shè)p是奇素數(shù),H,n,s,l為整數(shù),滿足1≤H≤p,n≥2以及(n,p)=(l,p)=1.則有
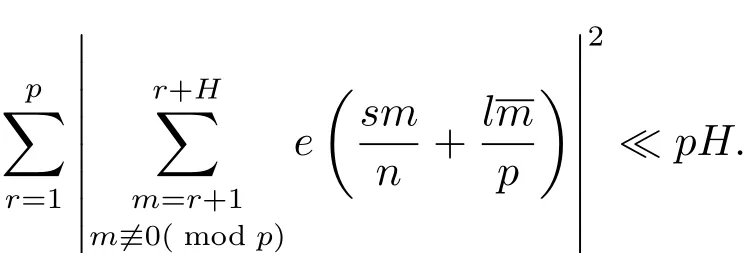
證由剩余系的性質(zhì)可得
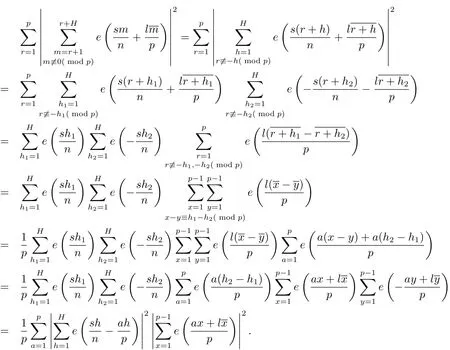
再由Kloosterman和的經(jīng)典估計,可得
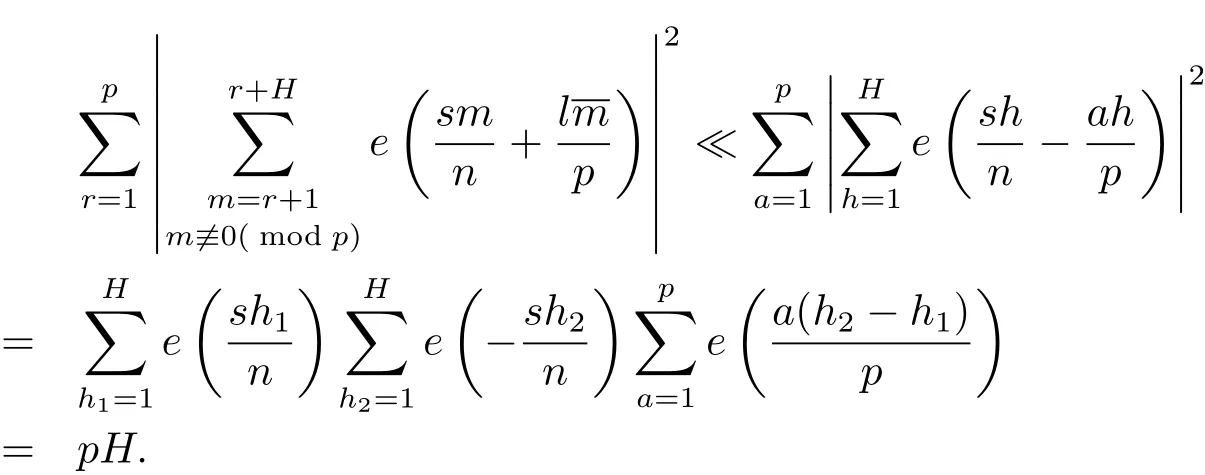
引理2.3設(shè)p是奇素數(shù)是互不相交的子區(qū)間,且對任意的j滿足其中H ≤p為正整數(shù).設(shè)n,s,l為整數(shù),滿足n≥2以及(n,p)=(l,p)=1.則有
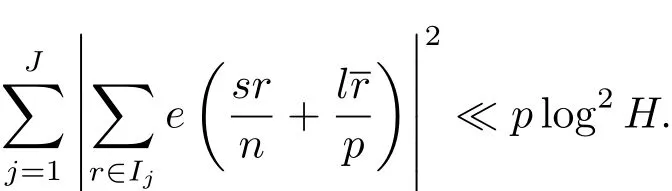
證利用引理2.2以及文獻[9]中的方法,不難證明引理2.3.為了完整起見,在此給出詳細的證明.
設(shè)Rj為集合Ij中的最小正整數(shù),并假設(shè)R1 容易證明 由1≤h≤H與Rj?H 因此有 再由柯西不等式,可得 對h取最大值,并對j求和,有 利用柯西不等式,有 上式兩邊對r求和,并結(jié)合引理2.2,有 結(jié)合(2.1)–(2.3)式,立即可得 易證 由三角恒等式,有 再由柯西不等式以及引理2.1可得 因此 另一方面,由三角恒等式有 再由柯西不等式以及引理2.3可得 其中 hαi=min({α},1?{α}).記m=sp?ln.則當(dāng)s取遍模n的完全剩余系,l取遍模p的簡化剩余系時,m取遍模np的完全剩余系中與p互素的整數(shù).因此 結(jié)合(3.1)–(3.4)式,立即可得 定理1.1證畢.
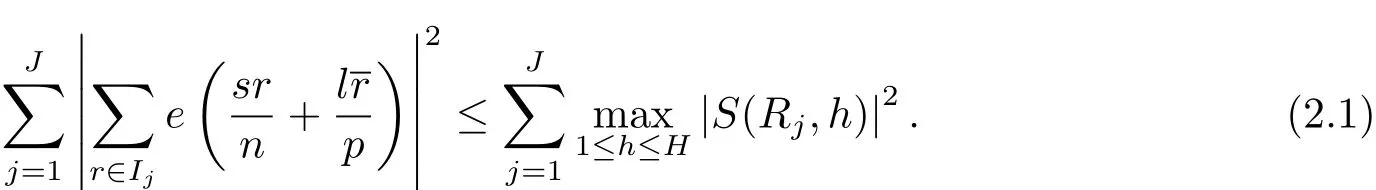
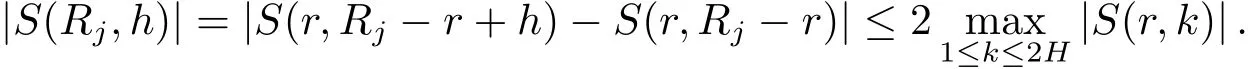
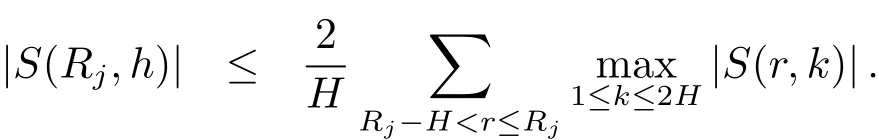

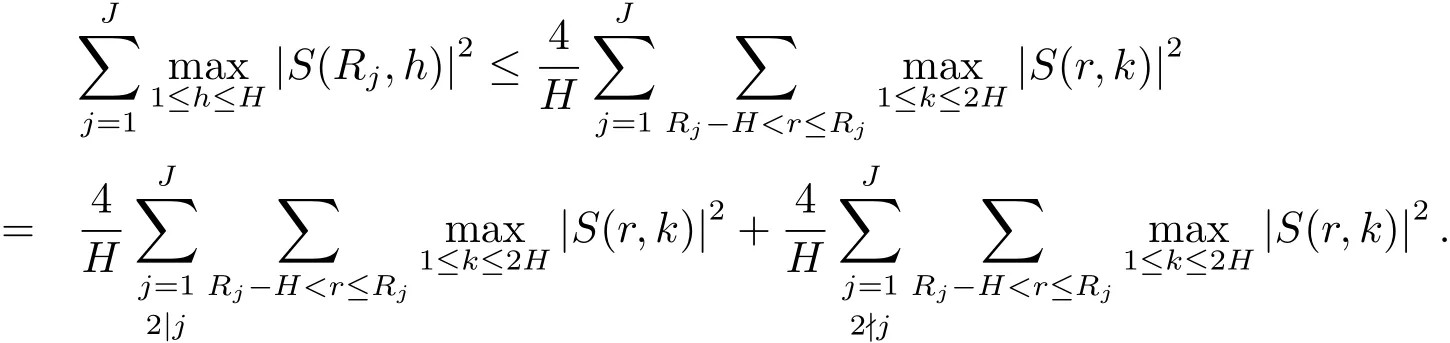
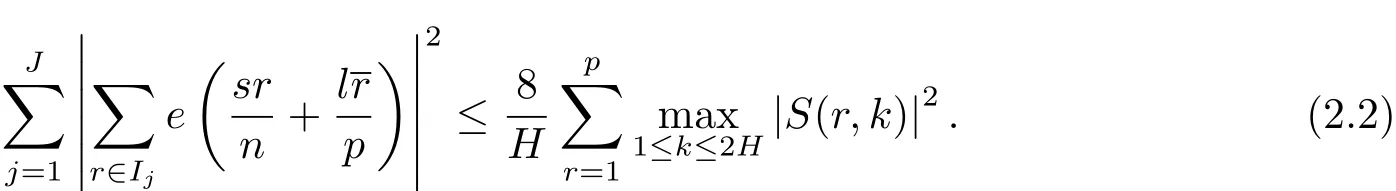
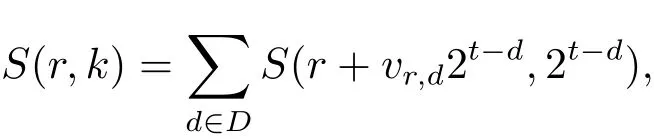
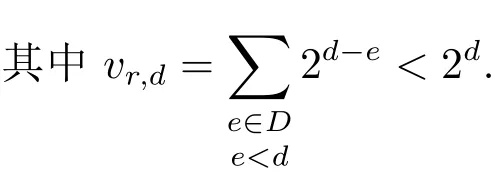
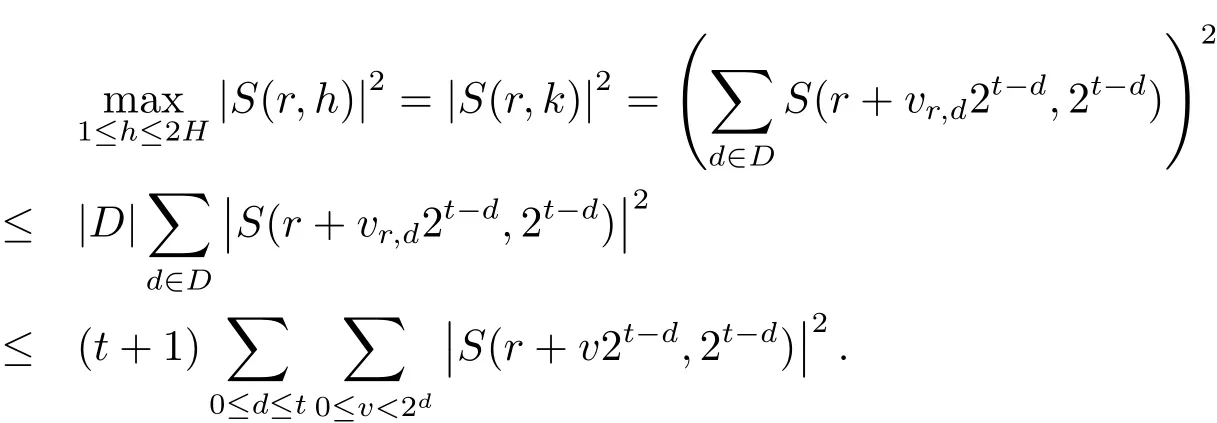
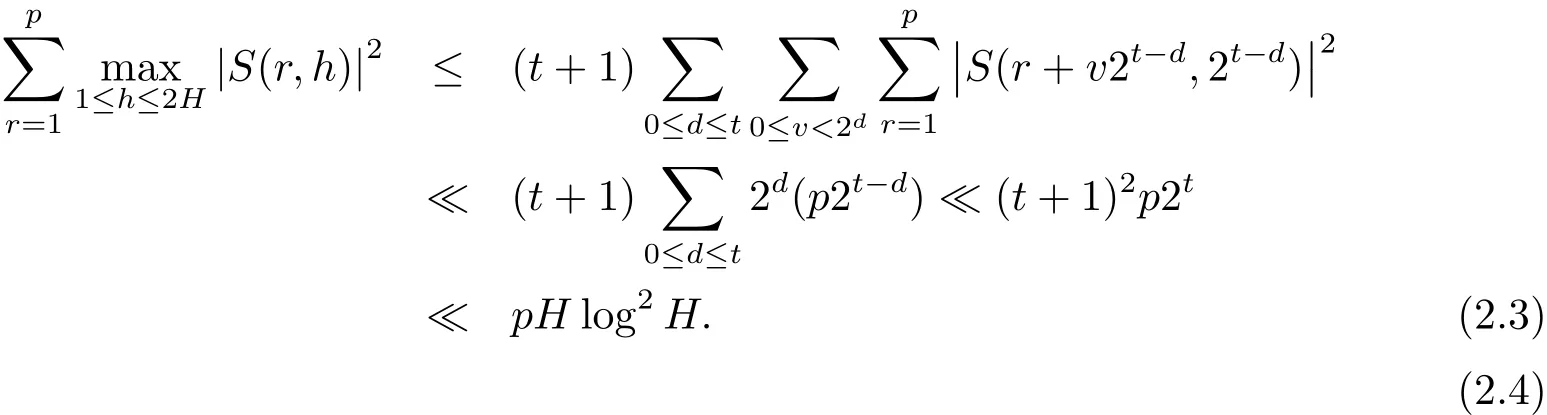
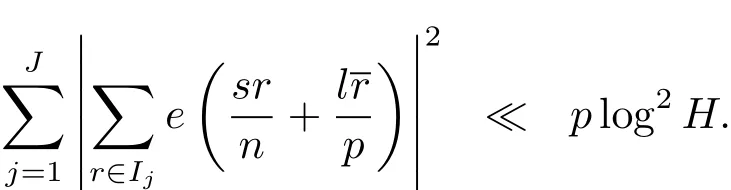
3 定理1.1的證明