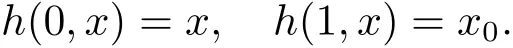MULTIPLICITY OF POSITIVE SOLUTIONS FOR QUASI-LINEAR ELLIPTIC EQUATIONS INVOLVING CONCAVE-CONVEX NONLINEARITY AND SOBOLEV-HARDY TERM
DU Ming, LIU Xiao-chun
(School of Mathematics and Statistics, Wuhan University, Wuhan 430072, China)
Abstract: In this paper, we investigate the quasi-linear elliptic equations involving concaveconvex nonlinearity and Sobolev-Hardy term. By using the theory of the Lusternik-Schnirelmann category and the relationship between the Nehari manifold and fibering maps, we get some improvement on existence and multiplicity of positive solution.
Keywords: subcritical Sobolev-Hardy exponent; Nehari manifold; sign-changing weight;concave-convex nonlinearity
1 Introduction
In this paper, we consider the following equation

(A1)with f±(x) = ±m(xù)ax{±f(x),0}0 and there exists a positive constant rfsuch that

(A2) g ∈C(RN) withand there exists constants rg1,rg2with 0 and Such kind of problem arised from various fields of geometry and physics and was widely used in the applied sciences. We refer to [1–3] for details on the description about the background. Elliptic problems on bounded domains involving concave-convex nonlinearity were studied extensively since Ambrosetti, Brezis and Cerami [4] considered the following equation where 1 < q < 2 < p2?, μ > 0. They found that there exists μ0> 0 such that (1.2)admits at least two positive solutions for μ ∈(0,μ0), a positive solution for μ = μ0and no positive solution exists for μ > μ0(see also Ambrosetti, Azorero and Peral [5, 6] for more references therein). In recent years, several authors studied semilinear or quasilinear problems with the help of Nehari manifold (see [7–9]). In particular, Lin [9] studied the following critical problem where ? ?RN(N3) is a bounded domain with smooth boundary,and 1 Actually,Fan and Liu[10]established multiple positive solutions of standard p-Laplacian elliptic equations without Hardy term on a bounded domain ? in RN. Some other theorems for p-Laplacian elliptic equations without Hardy term can be found in [11, 12]. Hsu and Lin[13] studied the following critical problem via generalized Mountain Pass Theorem [14] However, little is done on RNfor the operatorinvolving the concave-convex nonlinearity. Since the embedding is not compact on RNand the weight functions f and g are sign-changing, we will discuss the concentration behavior of solutions on the corresponding Nehari manifold to overcome these difficulties. Moreover,we get some improvement on multiplicity of positive solutions via the theory of Lusternik-Schnirelmann category (see [15]). Throughout our paper,we denote bythe completion ofwith respect to the standard norm. The functionis said to be a solution of problem (1.1) if u satisfies Then Iμ(u) is well-defined onand belongs to Problem (1.1) is related to well-known Caffarelli-Kohn-Nirenberg inequality in [16] If b=a+1, then p?(a,b)=p and the following Hardy inequality holds [17] which is equivalent to the usual norm We get our main result as follows. Theorem 1.1Suppose that the functions f and g satisfy condition(A1)and(A2). Let where Sλis the best Sobolev constant for the embedding ofinto Lr(RN) and defined by Then (i) for μ∈(0,L2), (1.1) has at least two positive solutions incorresponding to negative least energy; (ii) there exists μ0∈(0,L2) such that for μ ∈(0,μ0), (1.1) has at least three positive solutions inincluding two with positive energy. The paper is organized as follows: in Sections 2–4, based on some related preliminaries,we develop the description of Palais-Smale condition and the estimate of corresponding energy functional Iμ; in Section 5, we discuss the concentration behavior of solutions on Nehari manifold; in Section 6, we complete the proof of Theorem 1.1. Since the energy functional Iμin (1.6) is unbounded below onwe consider the functional on Nehari manifold Note that Nμcontains all nonzero solutions of (1.1) and u ∈Nμif and only if Lemma 2.1The energy functional Iμis coercive and bounded below on Nμ. ProofFor u ∈Nμ, by the H?lder inequality and Sobolev embedding theorem, we can deduce where C is a positive constant depending on N,q,Sλand. This completes the proof. Define Then for u ∈Nμ, we have As in [18], we divide Nμinto three parts Then we have the following result. Lemma 2.2 ProofBy (2.1) we can easily derive these results. Then the following lemma is essential for the main result. Lemma 2.3(i) For all μ∈(0,L1), we haveand α+<0. (ii) If μ < L2, then we have α?> c0for some c0> 0. In particularfor all μ∈(0,L2). Proof(i) Suppose the contrary. We may assume that there exists μ?∈(0,L1) such thatThus,for each,by the H?lder and Sobolev inequalities,we can obtain that is, and so But (2.1) implies that which means Combined (2.4) and (2.5), we have This contradicts to μ?∈(0,L1). Therefore,andfor μ ∈(0,L1). and so or Then for μ∈(0,L2), we have wher e This implies, for μ∈(0,L2), α+<0 Now we introduce the following function mu:R+→R in the form Clearly, tu ∈Nμif and only ifand It is obvious that if tu ∈Nμ, thenHence,if and only if(or <0). and mustrictly increases on (0,tmax) and decreases on Furthermore, since μ∈(0,L1), we have Thus, we have the following lemma. Lemma 2.4For each u ∈){0}, we have Proof(i) The equationadmits a unique solution t?>tmaxandholds by Lemma 2.3. (iii) By the uniqueness and extremal property of t?(u), we have t?(u) is a continuous function for u ∈ Thus, the proof is completed. Remark 2.5If μ=0, by Lemma 2.4 (i),=?and so Now we consider the limiting problem and the corresponding energy functionalis defined by Proposition 3.1Forproblem (3.1) has radially symmetric ground states satisfying where ci(i=1,2) are positive constants and a(λ),b(λ) are the zeros of the function Furthermore, there exist the positive constants c3,c4such that ProofAs in [19], we can prove that the limiting problem (3.1) has radially symmetric ground states, by which Sλcan be achieved. Let u(ξ) be a radial solution to (3.1). Then we get that Set Then we can obtain the following system The rest of the proof follows exactly the same lines as that of the limiting problem (3.1) in[19], here we omit it. By Proposition 3.1, we can easily derive the minimizing problem where For our purpose,the functional Iμis said to satisfy the(P.S.)ccondition if any sequencesuch that as n →∞, contains a convergent subsequence inThen the following proposition develops a precise description for the (P.S.)c-sequence of Iμ. Proposition 3.2(i) If μ∈(0,L1), then Iμhas a (P.S.)α-sequence (ii) If μ∈(0,L2), then Iμhas a (P.S.)α?-sequence ProofThe proof is similar to the argument of Proposition 3.3 in [20]. Now, we establish the existence of a local minimizer for Iμon Nμ. Proposition 3.3Forμ∈(0,L1),the functional Iμhas a minimizersatisfying ProofBy Proposition 3.2 (i), there exists a minimizing sequence {un}n∈N?Nμsuch that where o(1) →0 as n →∞. Since Iμis coercive on Nμ, we get that {un} is bounded inIf necessary to a subsequence, there existssuch that as n →∞, Moreover, by the Egorov Theorem and Hlder inequality, we have Consequently, passing to the limit in, by (3.7) and (3.8), we have Furthermore, since un∈Nμ, we can deduce that which implies that Next, we will show, up to a subsequence, thatstrongly inandIn fact, by the Fatou’s lemma, it follows that which is a contradiction. Sinceand, we may assume thatis a nontrivial nonnegative solution of (1.1). By Harnack inequality, it follows thatin RN. Finally, by (2.1) and the H?lder inequality, we can obtain Let ul=u0(x+le),for l ∈R and e ∈SN?1,where u0(x)is a radially symmetric positivesolution of (3.1) such that Then we have the following result. Lemma 3.4 We refer to the argument of Lemma 4.2 in He and Yang (see [21]). The following statement is paramount to prove our main result. Proposition 4.1For μ∈(0,L2), we have ProofLetbe a positive solution of (1.1) in Proposition 3.3. Then we obtain Since and There exist 0 Thus we only need to show that there exists l0>0 such that for l>l0, we have For u,v >0, we can remark that (u+v)r?ur?vr0, and so From condition (A1), (A2) and (3.5), we can obtain and Since 0 < rg2< min{rf?N,rg1?N} and t1tt2, by (4.1)–(4.8), we can find l0> 0 such that In order to complete the proof of Proposition 4.1, it remains to show that there exists a positive number t?such that. Let Next we claim that there exists t0> 0 such thatIn fact, we find a constant c > 0 such thatfor each t > 0. If not, then we may assume that there exists a sequence {tn}n∈Nsuch that tn→∞and Then we have which contradicts the fact that Iμis bounded below on Nμ. Let By (4.4) and Lemma 3.4, we have, as l →∞, Thus there exists l0>0 such that for l>l0, we get Then we have the following result. Theorem 4.2For μ ∈(0,L2), (1.1) has a positive solutionsuch that ProofBy Ekeland’s variational principle [22], there exists a minimizing sequencesuch that In this section, we discuss the concentration behavior of solutions to (1.1) so that we can get the proof of Theorem 1.1 (ii). Lemma 5.1We have Furthermore,(1.1)does not admit any solution w0∈such that I0(w0)= ProofBy Lemma 2.4, there exists the unique t?(ul) > 0 such that t?(ul)ul∈N0for all l>0, that is, Since and By (5.2)–(5.4), we have t?(ul)→1 as l →∞. Thus Then we can obtain For u ∈N0, by Lemma 2.4 (i), Moreover, there exists a unique t∞>0 such that t∞u ∈N∞. Thus, In order to show that (1.1) does not admit any solution w0such thatwe argue by the contrary. By Lemma 2.4(i), we haveMoreover, there exists a unique tw0>0 such that tw0w0∈N∞. Thus we obtain By the Lagrange multiplier and the maximum principle, we may assume that tw0w0is a positive solution of (1.1). This contradiction completes the proof. Lemma 5.2Assume that {un} is a minimizing sequence in N0for I0. Then Furthermore, {un} is a (P.S.) ProofFor each n, there exists a unique tn>0 such that tnun∈N∞, that is, By Lemma 2.4 (i), we have and Next, we will show that there exists M > 0, c0> 0 such that tn> c0for n > M. Suppose the contrary. Then we may assume tn→0 as n →∞. As in the proof of Lemma 2.3, we know thatis uniformly bounded and so→0 or I∞(tnun)→0. This contradicts the factfrom Lemma 5.1. Then we have and This implies andso Let be the filtration of the Nehari manifold Nμ. Then we have the following lemmas. Lemma 5.3There exists d0<0 such that for u ∈N0(d0), we have ProofSuppose the contrary. We may assume that there exists a sequence {un}n∈N?N0such thato(1). By Proposition 3.2 and the concentration-compactness principle (see [23, Theorem 4.1]), there exists a sequence {xn}n∈N?RNsuch that Now we will show that |xn|→∞as n →∞by contradiction. We may assume that {xn} is bounded and xn→x?for some x?∈RN. Then by (5.11), this contradicts the result of Lemma 5.2 (i). Hence we may assumee as n →∞,where e ∈SN?1. By the Lebesgue dominated convergence theorem, we have This contradiction completes the proof. By (2.1) and Lemma 2.4 (i), for eachthere exists the uniquesuch thatandThen we have the following result. Lemma 5.4Let For each μ∈(0,L2) and, we have ProofForwe distinguish from the following distinctive cases. Case(i)Since T >1, we have Case(ii)Since and by Lemma 2.2 (iii), we have Moreover, from the argument in the proof of Lemma 2.2, we have Thus, by (5.12)–(5.14), we have This completes the proof. Lemma 5.5There exists μ0∈(0,L2) such that for each μ∈(0,μ0) and ProofForby Lemma 2.4 (i), there existssuch thatN0. Moreover, by Lemma 5.4 and the H?lder inequality and Sobolev embedding theorem,we have or so by Lemma 2.1, for μ ∈(0,L2) and, there exists c?independent of μ such thatThus, Then by Lemma 5.3, we have and this implies The proof is completed. In this section, we will follow an idea in [24] to prove our main result. For c ∈R+, we denote Then we try to show that for a sufficiently small σ >0, we have Here‘cat’means the Lusternik-Schnirelmann category[15]. First,let us recall its definition. Definition 6.1A non-empty, closed subset Y is contractible in a topological spaceXif there exists h ∈C([0,1]×Y,X) such that for some x0∈X, Definition 6.2Let Y1,Y2,··· ,Ykbe closed subsets of a topological spaceX. The category ofXis the least integer k such that Yjis contractible inXfor all j anddenoted by cat(X). When there do not exist finitely many closed subsets Y1,Y2,··· ,Yk?Xsuch that Yjis contractible inXfor all j and=X, we denote cat(X)=∞. We need the following lemmas (see Theorem 2.3 in [25] and Lemma 2.5 in [24]). Lemma 6.3LetXbe a Hilbert manifold and F ∈C1(X,R). Assume that there are c0∈R and k ∈Nsuch that (i) F satisfies the Palais-Smale condition for energy level Then F has at least k critical points in Lemma 6.4LetXbe a topological space. Assume that there are ? ∈C(SN?1,X)and ψ ∈C(X,SN?1) such that ψ ?? is homotopic to the identity map of SN?1, that is,there exists h ∈C([0,1]×SN?1,SN?1) such that h(0,x) = (ψ ??)(x), h(1,x) = x. Then cat For l>l0, we define a mapby Lemma 6.5There exists a sequence {σl}?R+with σl→0 as l →∞such that ProofBy Proposition 4.1, for l>l0, we haveand Since ?μ(SN?1)is compact andthe conclusion holds. From Lemma 5.5, we define a barycenter map,by Then we have the following result. Lemma 6.6Letμ0be as in Lemma 5.5. Then forμ∈(0,μ0),there exists l?>l0such that the map is homotopic to the identity operator. ProofDenote as an extension of ψμ. Since ul∈supp ψμfor all e ∈SN?1and large enough l, we may assume γ :[s1,s2]→SN?1is a regular geodesic between ψμ(ul) andsuch that By an argument similar to Lemma 5.3, there exists l?l0such that for all e ∈SN?1, l>l?and θ ∈We define by as θ →1?. and for all e ∈SN?1and l>l?. This completes the proof. Lemma 6.7For μ ∈(0,μ0) and l > l?, the energy functional Iμadmits at least twocritical points in ProofIt is easy to deduce from Lemmas 6.3, 6.4, 6.6 and Proposition 3.2. Proof of Theorem 1.1Now we can complete the proof of Theorem 1.1 (i) by Proposition 3.3 and Theorem 4.2; (ii) from Proposition 3.3 and Lemma 6.7, (1.1) has at least three positive solutions









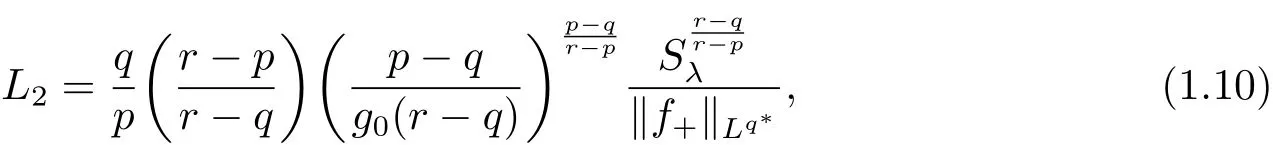

2 Preliminaries





























3 Palais-Smale Condition























4 The Estimates of Energy

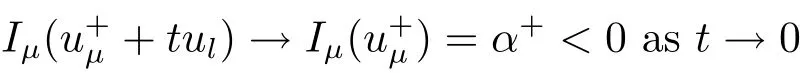

















5 Concentration Behavior













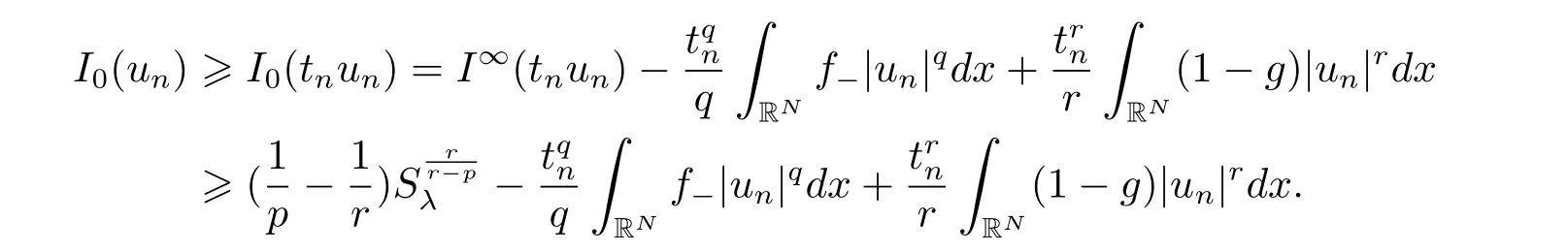






















6 Proof of Theorem 1.1