非緊區(qū)域上算子值再生核的Mercer定理
陳文健
(煙臺(tái)大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院, 山東 煙臺(tái) 264005)
1 引言及預(yù)備知識(shí)
眾所周知,再生核與再生核Hilbert空間理論已經(jīng)被廣泛的應(yīng)用到機(jī)器學(xué)習(xí)領(lǐng)域,尤其在單任務(wù)學(xué)習(xí)領(lǐng)域的應(yīng)用更為成功[1-5].隨著數(shù)據(jù)維數(shù)的不斷提高,多任務(wù)學(xué)習(xí)已經(jīng)漸漸的成為機(jī)器學(xué)習(xí)領(lǐng)域重要的研究課題.本文研究多任務(wù)學(xué)習(xí)中的算子值再生核以及向量值再生核Hilbert空間理論,其中被重構(gòu)的函數(shù)來自一個(gè)Hilbert空間[6-8].先簡單回顧一下算子值Mercer核的概念,這是本文主要研究的對(duì)象.令(X,ρ)表示一個(gè)度量空間,其中度量為ρ.令H表示上的Hilbert空間,其內(nèi)積為〈·,·〉H;B(H)表示由所有H上的連續(xù)線性算子構(gòu)成的Banach空間.如果映射K:X×X→B(H)滿足:
(i)K是對(duì)稱的,即對(duì)于任意的x,y∈X都有K(x,y)=K(y,x);
(ii)K相對(duì)于由度量ρ誘導(dǎo)的拓?fù)湓赬×X上是連續(xù)的;
(iii)K是正定的,即對(duì)于任意的{x1,…,xn}?X和{v1,…,vn}?H都有
那么K稱為B(H)值Mercer核.
根據(jù)Riesz表示定理知道對(duì)于任何一個(gè)B(H)值Mercer核K,存在唯一的Hilbert空間HK,其包含X上所有H值函數(shù),內(nèi)積和范數(shù)分別為〈·,·〉HK和‖·‖HK,且滿足
K(·,x)v∈HK, ?x∈X,v∈H
(1)
和
〈f(x),v〉H=〈f,K(·,x)v〉HK,
?f∈HK,x∈X,v∈H.
(2)
稱HK為向量值再生核Hilbert空間,K為其算子值再生核,且稱等式(2)為HK的再生性質(zhì).
對(duì)于數(shù)量值再生核有著名的Mercer定理[9],而對(duì)于算子值再生核以及其對(duì)應(yīng)的向量值再生核Hilbert空間的研究可以追溯到文獻(xiàn)[10].另外,文獻(xiàn)[11-13]對(duì)各種底空間X也進(jìn)行了深入地研究.特別地,在文獻(xiàn)[13]中,Mercer定理被推廣到具有有限測度的非緊區(qū)域上的算子值再生核上.本文的主要目標(biāo)是建立具有σ有限的非緊區(qū)域上的算子值再生核上的Mercer定理.對(duì)于具有σ有限的非緊區(qū)域上的數(shù)量值再生核上的Mercer定理可參考文獻(xiàn)[14].
多任務(wù)學(xué)習(xí)近幾年已經(jīng)成為機(jī)器學(xué)習(xí)領(lǐng)域熱門的研究領(lǐng)域,其中要學(xué)習(xí)的函數(shù)大多都是非緊區(qū)域上的向量值函數(shù).本研究結(jié)果可以給多任務(wù)學(xué)習(xí)領(lǐng)域提供一些堅(jiān)實(shí)的數(shù)學(xué)理論基礎(chǔ)和新的研究方向.
為了給出主要結(jié)果,先回顧一下向量值函數(shù)的積分的概念.對(duì)于向量值函數(shù)的積分更多的理論可以參考文獻(xiàn)[15-16].假設(shè)X是一個(gè)局部緊的度量空間,以及(X,F,μ)為一個(gè)測度空間,其中μ是F上的Borel測度.先從向量值函數(shù)的Bochner積分開始,函數(shù)f:X→H稱為是H值簡單函數(shù),如果
(3)
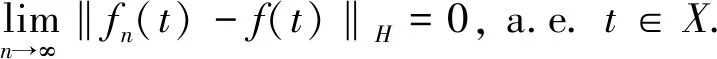
(4)

與數(shù)量值函數(shù)的Lebesgue空間類似,有下面的向量值函數(shù)情形的Lebesgue空間的定義.令L2(X,μ;H)表示包含所有X上H值Bochner可積的函數(shù)f的集合,且滿足
2 非緊區(qū)域上算子值再生核的Mercer定理
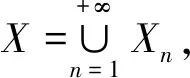
對(duì)于B(H)值Mercer核K,定義算子LK如下:
算子LK稱為由算子值核K定義的積分算子.假設(shè):
A1: 對(duì)于任意的x∈X和v∈H,K(x,·)v∈L2(X,μ;H);
A2:LK是L2(X,μ;H)上的有界正定算子;
A3:LK有可數(shù)個(gè)正特征值{λj},其對(duì)應(yīng)的標(biāo)準(zhǔn)正交特征向量為{φj}.
在上面的假設(shè)下,有命題1.
命題1 如果函數(shù)f:X→H是連續(xù)的且支撐在某個(gè)Xn0上,那么LKf∈HK.另外,對(duì)于任意的h∈HK都有
(5)
證明對(duì)于任意的x∈X,有
對(duì)于任意的x∈X,由K(x,·)和f都是連續(xù)的可得K(x,·)f也在X上連續(xù).因此對(duì)于任意的Φ∈H*有Φ(K(x,·)f)是可測的,從而K(x,·)f是弱可測的.另外,由H是可分的和Pettis定理得K(x,·)f是可測的.所以由Xn0的緊性有K(x,·)f在Xn0上是Bochner可積的.

對(duì)于任意x∈X,因?yàn)镵(x,·)f在Xn0上連續(xù)以及Xn0是緊的,所以K(x,·)f在Xn0上一致連續(xù).所以對(duì)于任意>0,存在δ>0使得只要ρ(s,t)<δ就有‖K(x,s)f(s)-K(x,t)f(t)‖H
-K(x,t)f(t)‖Hdμ(t)<,
這就推出對(duì)于任意的x∈X有
(6)
這里,tn,j是在En,j中任意選取的點(diǎn).
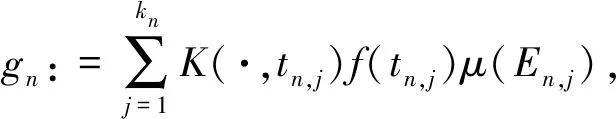
〈gn,gn〉HK-2〈gn,gm〉HK+〈gm,gm〉HK.
利用式(2)得
〈gn,gm〉HK=
其當(dāng)m,n→∞時(shí)收斂到
類似地,有
所以,推出序列{gn}是HK中的Cauchy列.從而結(jié)合式(6)得到LKf∈HK.

〈LKf,h〉HK=
其等于
即要證的結(jié)論成立.
引理1 設(shè)Cc(X;H)表示由所有具有緊支集的連續(xù)函數(shù)f:X→H構(gòu)成的線性空間,那么Cc(X;H)在L2(X,μ;H)中是稠密的.
證明設(shè)f為L2(X,dμ;H)中任意一個(gè)元素,只需證明對(duì)于任意>0,存在一個(gè)g∈Cc(X;H)使得
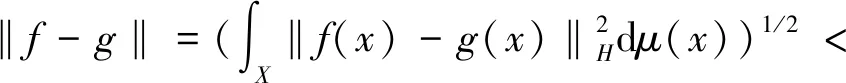
其中第二個(gè)等式由單調(diào)收斂定理得到.因此,存在一個(gè)正整數(shù)N使得
成立,而這可以推出
(7)
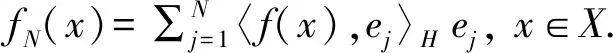
另一方面,顯然有fj∈L2(X,dμ),j∈.由Cc(X)在L2(X,dμ)中是稠密的,故存在gj∈Cc(X)使得
(8)

上式結(jié)合式(7)就完成了我們的證明.
命題2 對(duì)于任意的g∈L2(X,μ;H),有LKg∈HK,且
(9)
另外,對(duì)于任意的h∈HK∩L2(X,μ;H)有
〈LKg,h〉HK=〈g,h〉L2(X,μ;H).
(10)
證明由g∈L2(X,μ;H),可以選取Cc(X;H)中的序列{gn}使得{gn}在L2(X,μ;H)中收斂到g.由命題1有LKgn∈HK.另外,有
gm(s)-gn(s)〉Hdμ(s)=
這意味著{LKgn}是HK中的Cauchy列,從而在HK中有極限f.注意到再生性質(zhì)(1)和(2)得
〈LKgn-f,K(·,x)(LKgn(x)-f(x))〉HK≤
即
‖(LKgn)(x)-f(x)‖H≤
(11)
由Xm的緊性、K的連續(xù)性以及式(11)得{LKgn}在每個(gè)Xm上都一致收斂到f.

為了證明式(9)和(10),我們由式(5)計(jì)算得
以及
即要證明的結(jié)論成立.


有了上面的準(zhǔn)備工作,現(xiàn)在證明主要定理,即非緊區(qū)域上算子值再生核的Mercer定理.
定理1 設(shè)A1,A2和A3成立,那么對(duì)于任意的x,y∈X和u,v∈H有
〈K(x,y)v,u〉H=
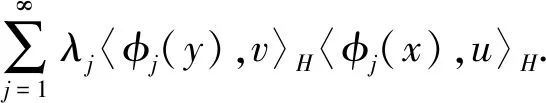
(12)
另外,固定u,v∈H,則上面的級(jí)數(shù)在Y1×Y2上一致和絕對(duì)收斂,這里,Y1和Y2都是X中的緊子集.

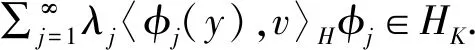

(13)
因?yàn)閧φj}是LK的標(biāo)準(zhǔn)正交特征向量,其對(duì)應(yīng)的特征值為{λj},有λj=〈λjφj,φj〉L2(X,μ;H)=〈LKφj,φj〉L2(X,μ;H)≤‖LK‖.結(jié)合式(13)得到

令
由上面的討論立即得到F(·,y,v)∈HK∩L2(X,μ;H).因此,對(duì)于任意的j有
0=〈F(·,y,v),φj〉HK=
由{φj}的完備性得F(x,y,v)=0對(duì)于變量x在X上幾乎處處成立.注意到μ是非退化的以及F(·,y,v)是連續(xù)的,有F(x,y,v)=0對(duì)于任意的x,y∈X和v∈H成立,即
再由內(nèi)積的連續(xù)性就得到式(12).
特別地,對(duì)于任意的x∈X和v∈H有
(14)
由K和φj的連續(xù)性,以及Dini定理[17]得式(14)右端的級(jí)數(shù)在任意緊子集Y1上一致收斂.另外,由Cauchy-Schwartz不等式得
由此得級(jí)數(shù)(13)在Y1×Y2上一致和絕對(duì)收斂,其中Y1和Y2為任意的緊子集.定理1得證.

