A prediction method for the performance of a low-recoil gun with front nozzle
Cheng Cheng, Chong Wang, Xiaobing Zhang
School of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing, 210094, China
Keywords:Interior ballistic Low recoil Rarefaction wave Prediction method Two-dimensional
ABSTRACT One of the greatest challenges in the design of a gun is to balance muzzle velocity and recoil, especially for guns on aircrafts and deployable vehicles.To resolve the conflict between gun power and recoil force,a concept of rarefaction wave gun (RAVEN) was proposed to significantly reduce the weapon recoil and the heat in barrel,while minimally reducing the muzzle velocity.The main principle of RAVEN is that the rarefaction wave will not reach the projectile base until the muzzle by delaying the venting time of an expansion nozzle at the breech. Developed on the RAVEN principle, the purpose of this paper is to provide an engineering method for predicting the performance of a low-recoil gun with front nozzle.First, a two-dimensional two-phase flow model of interior ballistic during the RAVEN firing cycle was established. Numerical simulation results were compared with the published data to validate the reliability and accuracy. Next, the effects of the vent opening times and locations were investigated to determine the influence rules on the performance of the RAVEN with front nozzle.Then according to the results above, simple nonlinear fitting formulas were provided to explain how the muzzle velocity and the recoil force change with the vent opening time and location. Finally, a better vent venting opening time corresponding to the vent location was proposed. The findings should make an important contribution to the field of engineering applications of the RAVEN.
1. Introductions
In the new modern military, weight reduction and power increase are the leading directions of future developments for guns.However, with the increasing muzzle velocity of guns, heavier mount is required to absorb the recoil during the firing cycle.One of the greatest challenges in the design of a gun is to balance the muzzle velocity and the recoil,especially for guns on aircrafts and deployable vehicles.To resolve the conflict between gun power and maneuvering characteristics, lots of reducing recoil weapons and devices have been developed over the last several decades,including [1e3]: soft recoil, Davis balance gun, muzzle brake,magnetorheological fluid technology.
The concept of rarefaction wave gun(RAVEN) was proposed by Dr. Kathe et al. [4,5] to balance the muzzle velocity and the recoil while firing.RAVEN is by the reason of rarefaction wave theory and has the similar structure to recoilless gun. It can significantly reduce the weapon recoil and the heat in barrel, while minimally reducing the projectile velocity.The main principle of RAVEN is that the rarefaction wave will not reach the projectile base until the muzzle by delaying the venting time of an expansion nozzle at the breech.
Studies over the past two decades have provided important results on RAVEN by experiments and theories.The first analysis of a RAVEN launcher on a 120 mm gun could theoretically impose 75%less recoil momentum and reduce 50% barrel heating [6,7]. Experimental validation using NATO standard 35 mm anti-aircraft ammunition was presented in the PhD thesis of Kathe [4]. It demonstrated that recoil reduction of RAVEN could reach more than 50%and overall barrel heating reduction can reach about 40%.A new 1-D code was written by Coffee [8] to model the firing process of RAVEN. A series of simulations were compared to the experiments of a 35 mm RAVEN.Then the 1-D code with a correct model of the nozzle was updated by Coffee [9] and applied to a 105 mm RAVEN. Zhang and Wang et al. carried out a number of investigations into the rarefaction wave gun with an expansion nozzle at the breech, for example, the two-phase flow analysis of RAVEN [10], the venting time of RAVEN [11], the back blast mechanism of different nozzles [12]and dynamic characteristics during the firing cycle of RAVEN [13]. Combining the rarefaction wave concept with front orifice recoilless rifle,several experimental and numerical attempts were made to a small caliber automatic weapon by Liao et al. [14]. The rarefaction wave gun with a font nozzle can maintain the muzzle velocity and reduce the recoil significantly, without changing the breech structure. But there are still some worth areas worth studying such as opening device,opening time, vent location, nozzle structure, multi-dimensional flow behavior, parameters influence law, etc.
Recently, investigators have examined several parameters which can affect the travel role of rarefaction wave.The rarefaction wave is seriously influenced by the opening times for the RAVEN with breech nozzle. However, in additional to the influence of the opening times,the rarefaction wave is affected by the vent locations for the RAVEN with front nozzle.Much uncertainty still exists about the relationship between the vent opening times and locations.The best opening time of vent without reducing the muzzle velocity can be confirmed by the vent location and the rarefaction wave propagation. But sometimes reducing the recoil impulse is a more important fact relative to the muzzle velocity. The number of combinations of different influence factors increases geometrically.All of these make the traditional numerical simulation of twophase flow interior ballistic has very huge calculation burden.
Nowadays advanced numerical simulation techniques of twophase flow have been developed to improve the computational performance [15e20] including computing efficiency, high-order accuracy, model simplification, especially for the non-equilibrium two-phase flow problem. However, the non-equilibrium phenomena such as velocity difference and temperature difference between two phases should be considered in the interior ballistic models of guns.The solid velocity is depended not only by the flow drag but also by the intergranular stress. Current advanced numerical techniques are not yet able to apply to the dense gas solid flow in guns directly and easily[21e24].In addition,until now very little attention has been paid to the rapid prediction method for the RAVEN performance, especially for the RAVEN with front nozzle.Moreover, multi-dimensional studies are necessary for the rarefaction wave gun with front nozzle. The rapid prediction method with multi-dimensional model will become even more important in the engineering applications of the RAVEN.
The purpose of this paper is to provide an engineering method for predicting the performance of a low-recoil gun with front nozzle.Firstly,A two-dimensional two-phase flow model of interior ballistic during the RAVEN firing cycle is established. The simulation results are compared with the published results to validate the reliability and accuracy.Next,the effects of the vent opening times and the locations are investigated to determine the influence rules on the performance of the RAVEN with front nozzle. Then simple nonlinear fitting formulas are provided to explain how the muzzle velocity and the recoil force change with the vent opening times and locations.Finally,a better vent opening time corresponding to the vent location for the RAVEN with front nozzle is suggested.
2. Theoretical models
The schematic of a typical rarefaction wave gun with front nozzle is shown in Fig.1. In contrast to traditional guns, there is a front Laval nozzle connected with the barrel.The propellant gas can flow through the orifice in the barrel. The orifice only opens at a specific time for the RAVEN structure shown in Fig. 1, unlike the front orifice recoilless rifle.The rarefaction wave can be controlled by this method.
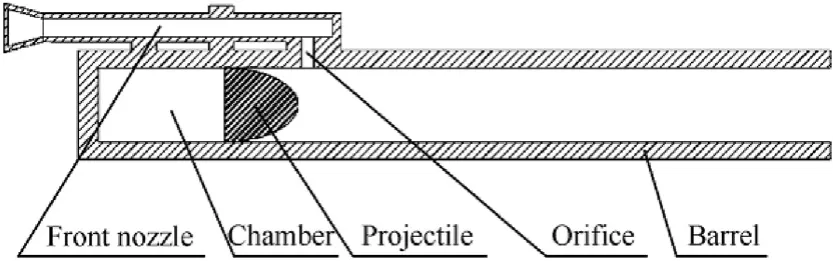
Fig.1. Schematic of a typical rarefaction wave gun with front nozzle.
The dense gas-solid reactive flow in guns should consider the differences between two phases,such as non-equilibrium velocity,non-equilibrium temperature, etc. The solid velocity is depended not only by the flow drag but also by the intergranular stress.In this paper,a unified mathematical model based on a modified two-fluid theory was established to describe the non-equilibrium two-phase flow characteristics in both barrel and nozzle. The conservation equations of mass and momentum were considered for both gas and solid phases.The energy conservation equation was considered for gas phase.The energy transfer for solid equation was considered in the solid temperature equation. The generalized governing equations of the multi-dimensional problem are given below.
The mass conservation equation of the gas phase

The mass conservation equation of the solid phase
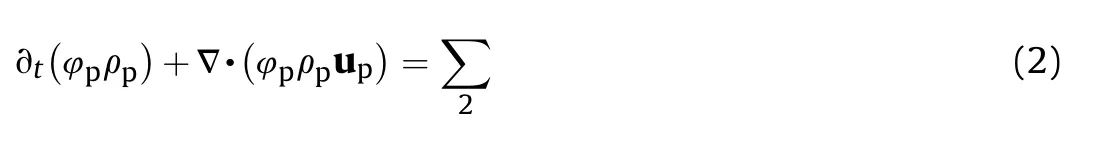
The momentum conservation equation of the gas phase
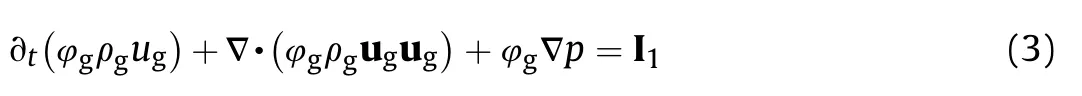
The momentum conservation equation of the solid phase
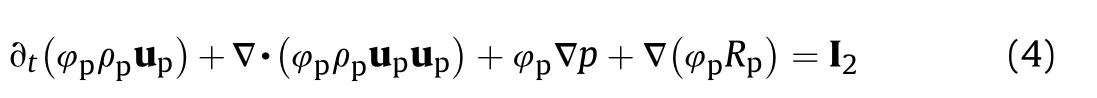
The energy conservation equation of the gas phase

where 4gand 4pare the gas and solid porosity,rgand rpare the gas and solid density,ugand upare the gas and solid velocity,p is the pressure, et_g?egt ug,ug=2 is the total energy per unit mass for gas,egis the gas internal energy, Rpis the intergranular stress.
The right terms are given by following equations,
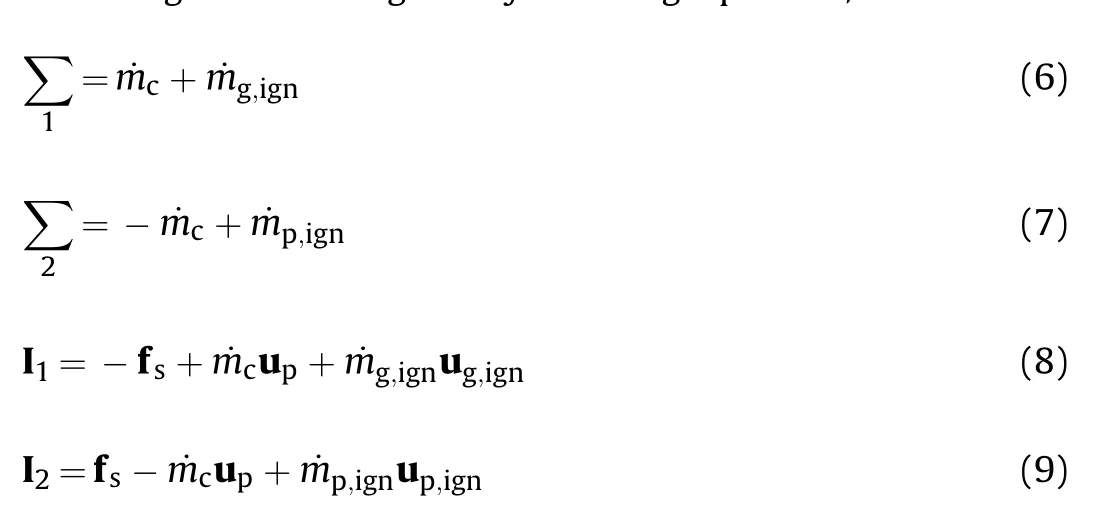
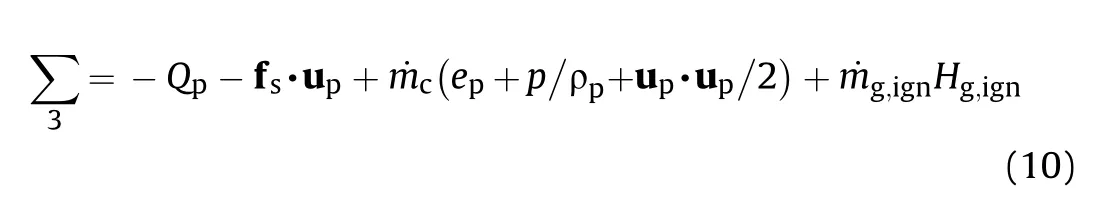
Considering the propellant is incompressible, the energy equation is obtained by the solid phase temperature calculation due to the heat transfer between two phases. The propellant begins to burn when the surface temperature reaches an ignition temperature.

where q is the interphase heat transfer per unit volume, apis the coefficient of temperature conductivity, lpis the thermal conductivity of particle,dt is the time step,and t is the total reaction time.
The interphase heat transfer includes convective heat transfer and radiative heat transfer, which are obtained by

where hcis the convective heat transfer coefficient, εpis the emissivity constant and s is the Stefan-Boltzmann constant.
Although the solid phase is assumed as incompressible, the propellant bed is still strongly compressed by the gaseous products and it could produce the deformation and relative movement.The intergranular stress equations are used to describe the compressible character between particles. The intergranular stress equation is given as following:

where cpis intergranular sound-speed,40is the settling porosity,c1is the sound speed in solid at settling porosity 40,K is the factor of stress attenuation. 4*represents the porosity value above when granular wave speed is zero.
The mass transfer between two phases is due to the propellant combustion. And the decomposition rate of propellant is obtained by
where Sp,Vpare the current surface area and volume of a propellant grain. _r is the burning rate, which can be given by following empirical linear burning law.

where a, b, n are constant obtained by experiments of propellant material.
A real gas equation of state is required to describe the thermodynamic model of propellant gas due to the high gas densities in
the chamber. The Noble-Abel equation provides a simple and reasonably accurate for combustion gas at the high densities and temperatures in guns [25].

where R is the specific gas constant,Tgis the gas temperature,b is the co-volume parameter.
A model for drag force proposed by Gough is used to calculate the interphase drag.

where dpis the effective diameter, Cfis the empirical coefficient.
3. Numerical methods
3.1. ALE model
As described physical process above,the two-dimensional twophase flow in the rarefaction wave gun is different from traditional gas and solid flow problem. It should consider the motion of the projectile. To reduce the computational cost and improve the accuracy, arbitrary Lagrangian-Eulerian (ALE) approach was applied to the specific problem interior ballistics in our previous work[26,27]. The arbitrary LagrangianeEulerian (ALE) approach which combines the advances of the Eulerian and Lagrangian descriptions is developed to deal with this moving boundary problem.
In this paper, a two-dimensional computational model in ALE form was used to describe the mass, momentum and energy equations of two-phase reactive process. The generalized governing equations for the two-dimensional two-phase flow problem should be expressed as conserved vectors in different directions for programming codes. The above governing equations are also transformed into ALE models with a two-dimensional axisymmetric form.

where r and z are the radial and axial directions respectively, flux vectors in vector directions F and G, the axisymmetric transform vector H are given in the following ALE forms.
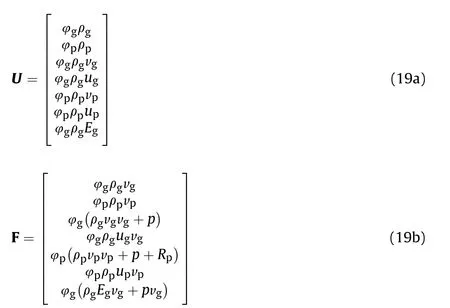
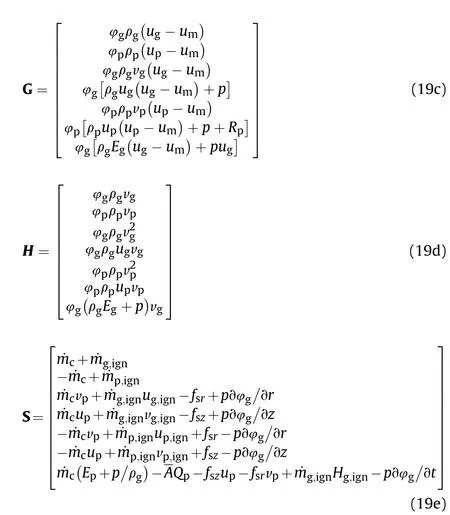
where ug,vg,upand vpare the gas and solid velocity in the axial and radial directions respectively,umare the moving boundary velocity in the axial direction. Here the moving boundary velocity should only be considered as the projectile velocity.
3.2. Numerical methods
The conservation equations for the specific interior ballistic problem are partial differential equations and contain convective parts and source terms respectively. In order to improve the simulation accuracy, these two parts were treated separately.Firstly, the convective terms were solved using finite volume method with two-dimensional discretization. Second order accuracy was achieved by using the monotonic upwind scheme for conservation laws [28]. The semi-implicit method for pressurelinked equations algorithm with a density correction is used to calculate the unsteady advection part [29e31]. To avoid spurious oscillations around discontinuities or shock,a limiter function was used. Based on the calculation results of convective terms, the fourth-stage and four-order Runge-Kutta method was used to calculate the source terms. Then the calculation for the next time step was carried out until the entire simulation ended.
3.3. Meshes and boundaries
Two-dimensional quadrangular meshes were generated for the entire fluid region. Two layers of fictitious cells surrounded the fluid region to keep second-order precision at the boundaries and be solved by the upwind scheme directly. Once the projectile begins, the computational domain should expand. The height of the cells adjacent to the projectile base increases as well. When the height of the layer reached a given limit,the layers of cell adjacent to the moving boundary were split and a layer was added.
Unlike a traditional gun, the specific condition should be considered at the nozzle exit. A fixed outlet pressure was held for the subsonic flow and the extrapolated condition for supersonic flow. The reflective boundary was used at all walls of the computational domain, even though the projectile started to move. The velocity of the projectile base was considered in the calculate variable values at the fictitious cells [28], as shown in following equation.

The projectile velocity was calculated by the Newton's second law involving the resistance loss.

where A is the cross-section area of the barrel,pbaseis the pressure at the base of projectile,41is the coefficient of resistance loss,m is the projectile mass.
4. Results and discussions
4.1. Validations
During the code programming, several validation tests were used to test the accuracy and reliability,such as the shock tube test,the source term test, the virtual AGARD gun. The AGARD gun has been widely used as a standard test to aid the development of interior ballistics in several countries. The detailed AGARD parameters can be found in the paper by Woodley [32] and comparisons of internal ballistics simulations of the AGARD gun from different countries were collected in this paper. Here simulation results from our code are compared with some published codes and detailed comparisons can be found in our other paper [33]. Comparisons between predicted and published results for the AGARD Gun are shown in Table 1. The predicted time histories of the AGARD Gun are shown in Fig. 2. The predicted results are in agreement with the expected ones. The differences between various codes are caused by the different grids and submodels including intergranular stress, interphase drag, etc. This has been studied by several researchers[34,35].
The grid convergence studies were also investigated to discuss the effect of the gird size in Fig. 3. The grid spacing varied from 2 mm to 10 mm. The relative error is decreased with the grid spacing. When the grid spacing is 4 mm, the relative error for the muzzle velocity is less than 0.3%. Although further increasing the grid size can reduce the error a bit, the computational time increases significantly. By balancing the computational time and numerical accuracy, the gird spacing size 4 mm is sufficient to ensure the numerical accuracy and the grid independent results.
4.2. Simulations of RAVEN with front nozzle
Based on the AGARD gun with a connected front nozzle which is like the structure in Fig.1,a rarefaction wave gun with front nozzle was designed to study the interior ballistic performance. The interior ballistic process of RAVEN with front nozzle is the same as the process of AGARD until the vent opens. These simulations in detail can be found in Ref.[33].Here only the simulation results in the barrel after the vent opens are provided.
4.2.1. Velocity distributions
Fig.4 and Fig.5 present velocity and streamline distributions of gas and solid phase at different times after the vent opening,respectively. In each diagram, the left part shows the velocity distribution and the right part shows the streamline. It is found thatthe radial effect is extremely obvious at the region near the vent.The gas and solid phases flow through the vent from the directions of both base and breech.Lagging of the solid phase velocity behind the gas velocity is clearly observed since the particles are dragged by the gas and the inertia of the particles is greater than that of the gas.Due to the flows in the opposite directions,there is an obvious region between the base and vent where the velocity equals zero.

Table 1 Results of different codes for the AGARD Gun.
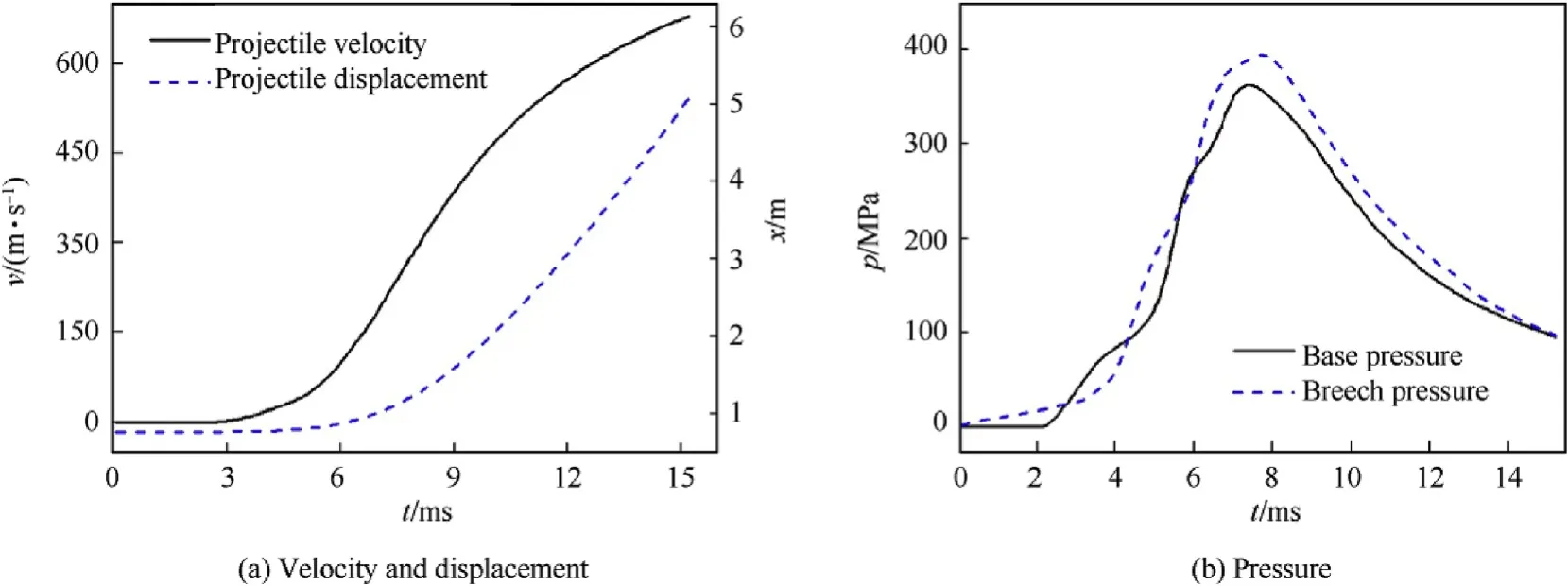
Fig. 2. Predicted results of the AGARD Gun.
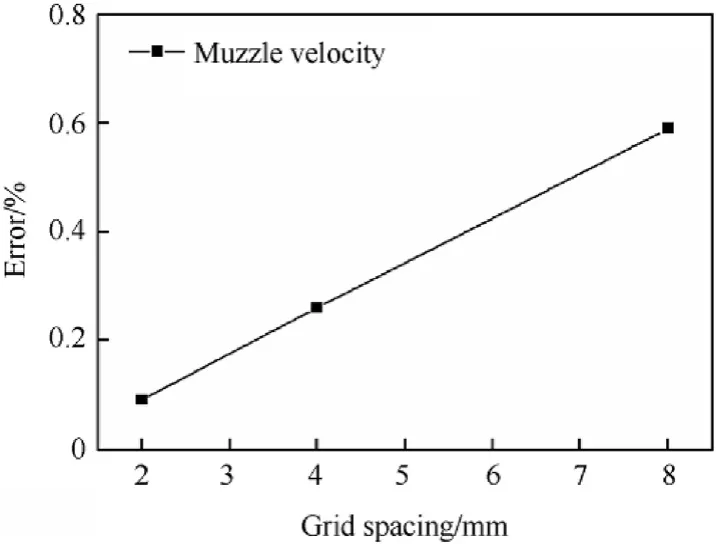
Fig. 3. Grid convergence curves.

Fig. 4. Contours and streamlines of gas velocity.
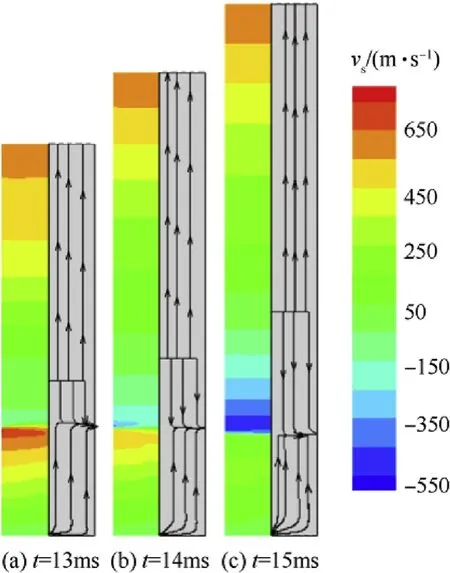
Fig. 5. Contours and streamlines of solid velocity.
4.2.2. Pressure distributions
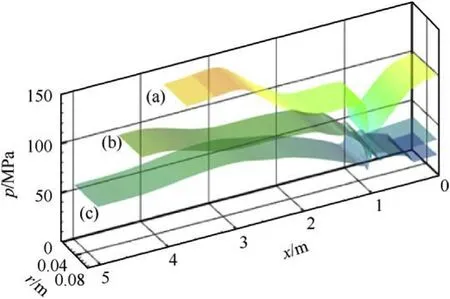
Fig. 6. Pressure distributions at different times.
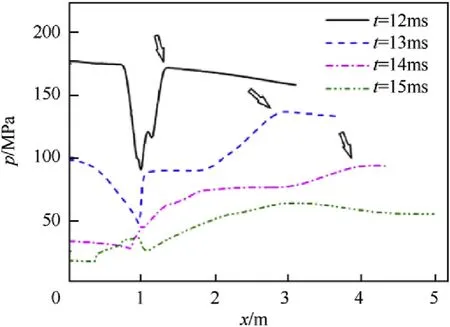
Fig. 7. Pressure distributions along the axis at r?0.04 m
The pressure distributions in the chamber at different times are shown in Fig. 6. The pressure distributions along the axis at r?0.04 m are shown in Fig. 7. With the projectile motion and the completing of some propellant combustion, the pressure in the chamber decreases with time.In particular,the pressure in the vent region drops rapidly.The obvious decrease can be easily found,and it also travels to the projectile base with time,which is identified by arrows in Fig.7.The rarefaction wave location can be tracked by this pressure development as well.Where the rarefaction wave reaches,the pressure will decrease rapidly. Before the rarefaction wave front, there is no obvious pressure change. If the rarefaction wave reaches the projectile base when the projectile just exits the muzzle, the muzzle velocity will not decrease. This is the key to realize the low recoil without reducing muzzle velocity.
4.2.3. Rarefaction wave and ballistic characteristics
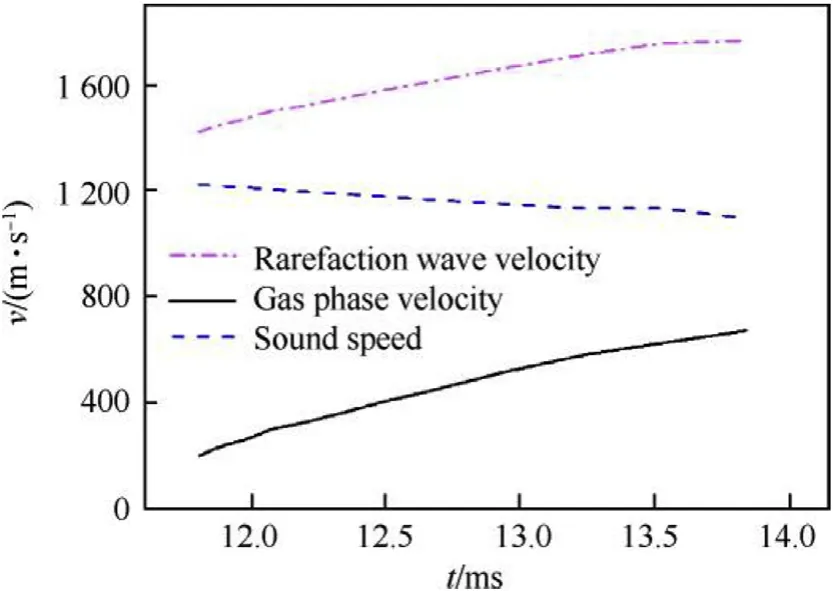
Fig. 8. Velocities at the rarefaction wave front.
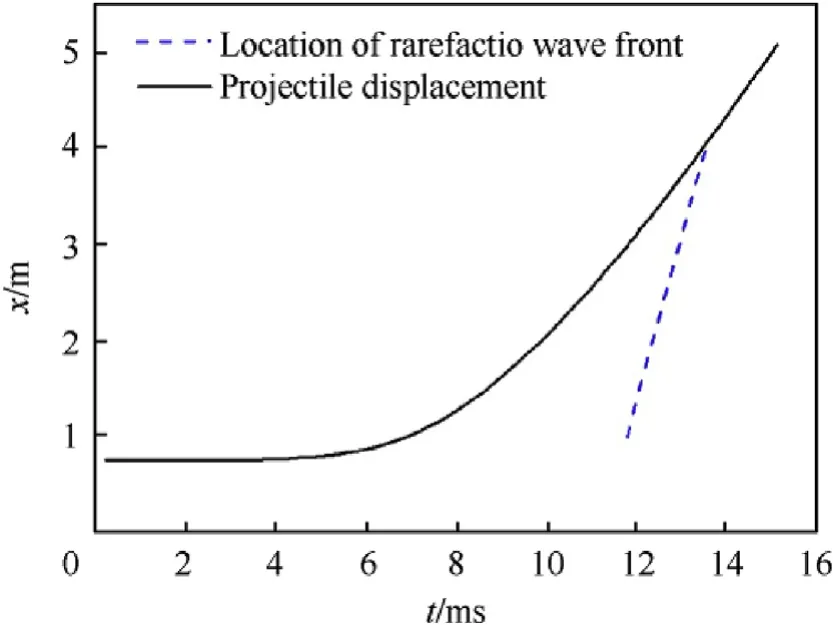
Fig. 9. Time histories of projectile and rarefaction wave front positions.
As described above,the rarefaction wave front position seriously affects the pressure and muzzle velocity Fig.8.The rarefaction wave velocity increases constantly due to both contributions from gas phase velocity and sound speed, even the sound speed decreases with time.Fig.9 shows the time histories of the projectile and the rarefaction wave front positions. The vent opened at time t?11.8 ms and the rarefaction wave reached the projectile base at 14.2 ms. At this time the projectile was still in the barrel, so the muzzle velocity should be reduced by the function of the rarefaction wave. Hence the current commonly used method for the prediction of vent opening time is not suitable for the RAVEN with front nozzle.
Fig.10 shows the comparisons of the projectile motion between the AGARD and the RAVEN. Fig.11 shows the comparisons of the recoil impulse between the AGARD and the RAVEN. Due to the rarefaction wave function, the muzzle velocity was reduced from 680 m/s to 667 m/s.There was about a 1.92%decrease in the muzzle velocity,but a 35.91%decrease in the recoil impulse was achieved.It can be also found that the muzzle velocity decrease was behind the recoil impulse drop. This is because the gas escaped from the vent nozzle immediately when the vent opened and the recoil impulse decreased soon. But the rarefaction wave took some time to reach the projectile base. This is how the RAVEN works.
4.3. Effects of different vent opening times and locations
The parameters of the additional chamber (such as the vent opening time and the vent location) can directly influence on the RAVEN performance. In this section, the effects of different parameters are discussed to guide the optimization design of the RAVEN and a new predicted method is proposed for engineering design.
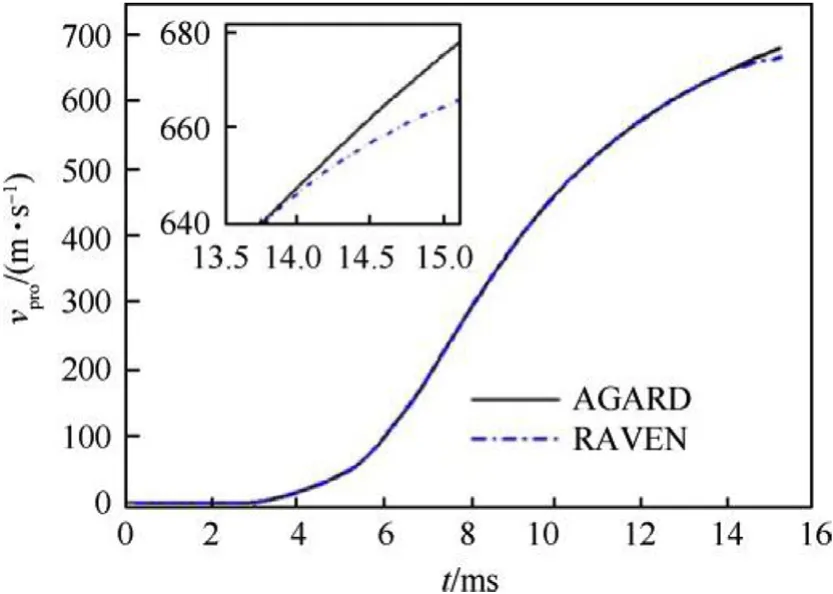
Fig.10. Comparisons of projectile motion between AGARD and RAVEN.
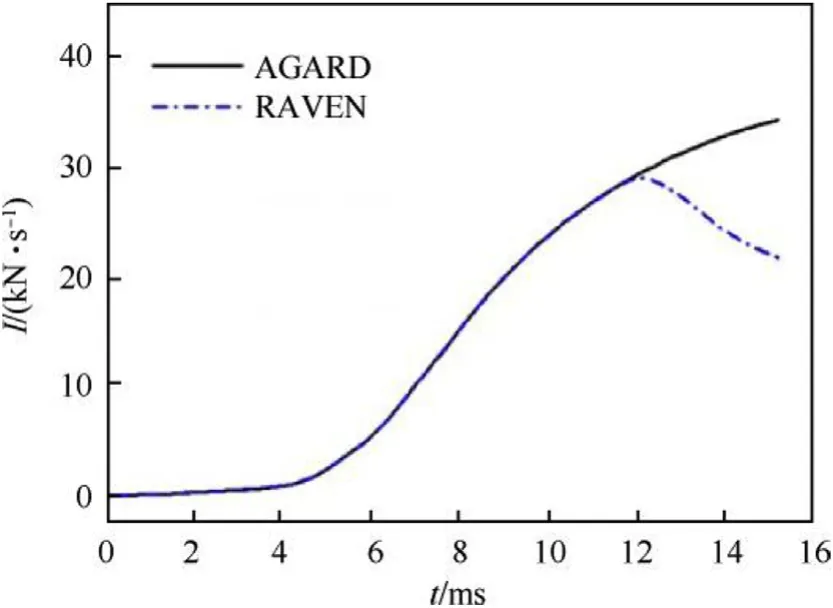
Fig.11. Comparisons of recoil impulse between AGARD and RAVEN.
4.3.1. Vent location
The vent usually located at the breech of the normal RAVEN and the vent location is a specific factor for the RAVEN with front nozzle.Hence the effect of the vent location was studied by increasing it from 1 m to 2.4 m, which means the distance from the vent to the breech. The vent opening times for different cases were the same.Fig.12 compares time histories of the muzzle velocity and the recoil impulse at different vent locations respectively.Some characteristic parameters and their rates of change such as the muzzle velocity,the recoil impulse at different vent locations are shown in Fig.13.With the increase of the distance from the breech to the vent, the muzzle velocity decreases and the recoil impulse increases. It is obviously not good for improving ballistic characteristics. Therefore,decreasing the distance between the vent and the breech will improve the interior ballistic characteristics of the RAVEN with front nozzle. But if the front nozzle located in the region of the chamber, it could cause the safety problem.
4.3.2. Vent opening time
It is obvious that the rarefaction wave propagation greatly depends on the vent opening time.The effect of the vent opening time was studied in Figs.14 and 15 by changing the vent opening time from 8.8 ms to 14.8 ms.With the increase of the vent opening time,the recoil impulse increased, and the muzzle velocity increased before about t?13 ms. After t?13 ms, the muzzle velocity remained almost the same.It means the rarefaction wave could not travel to the projectile base before the projectile left the muzzle.It is obvious that increasing the venting opening time can improve the muzzle velocity of RAVEN with front nozzle. Nevertheless, it goes against the improvement of the recoil impulse. Hence, the vent opening time should be chosen to match with the balance of muzzle velocity and recoil impulse.
4.3.3. Predicted method and optimized parameters

Fig.12. Time histories of ballistic characteristic at different vent locations.
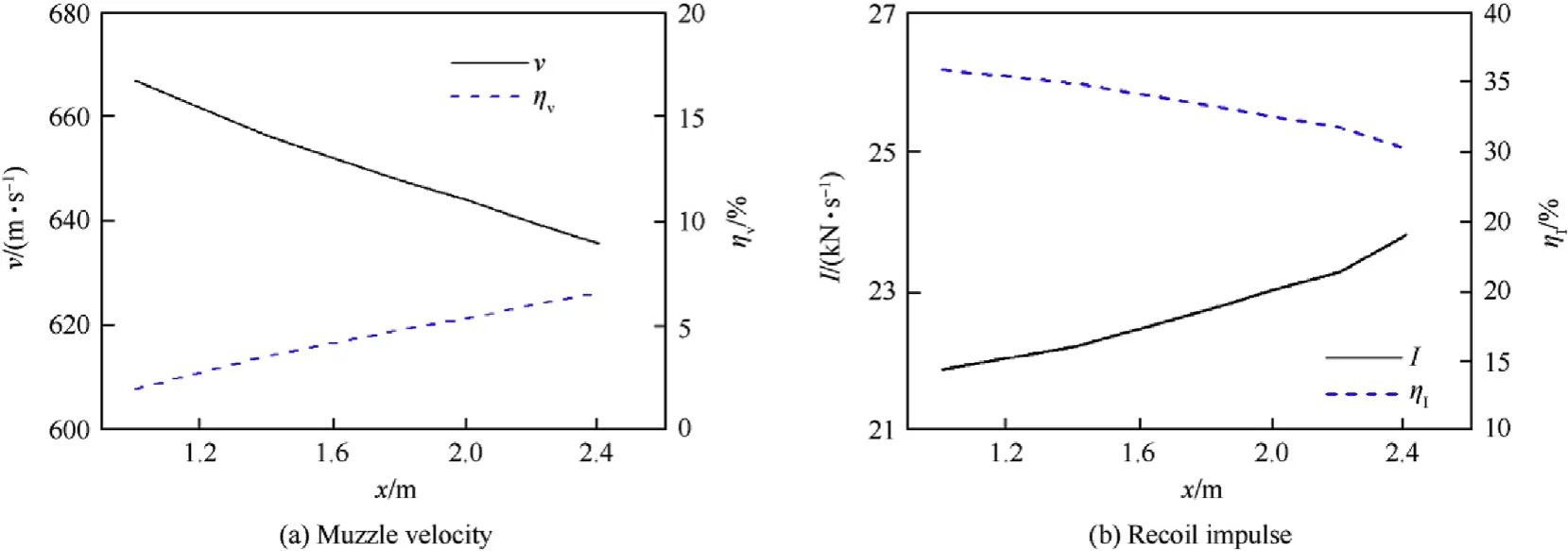
Fig.13. Ballistic characteristic and its rate of change at different vent locations.
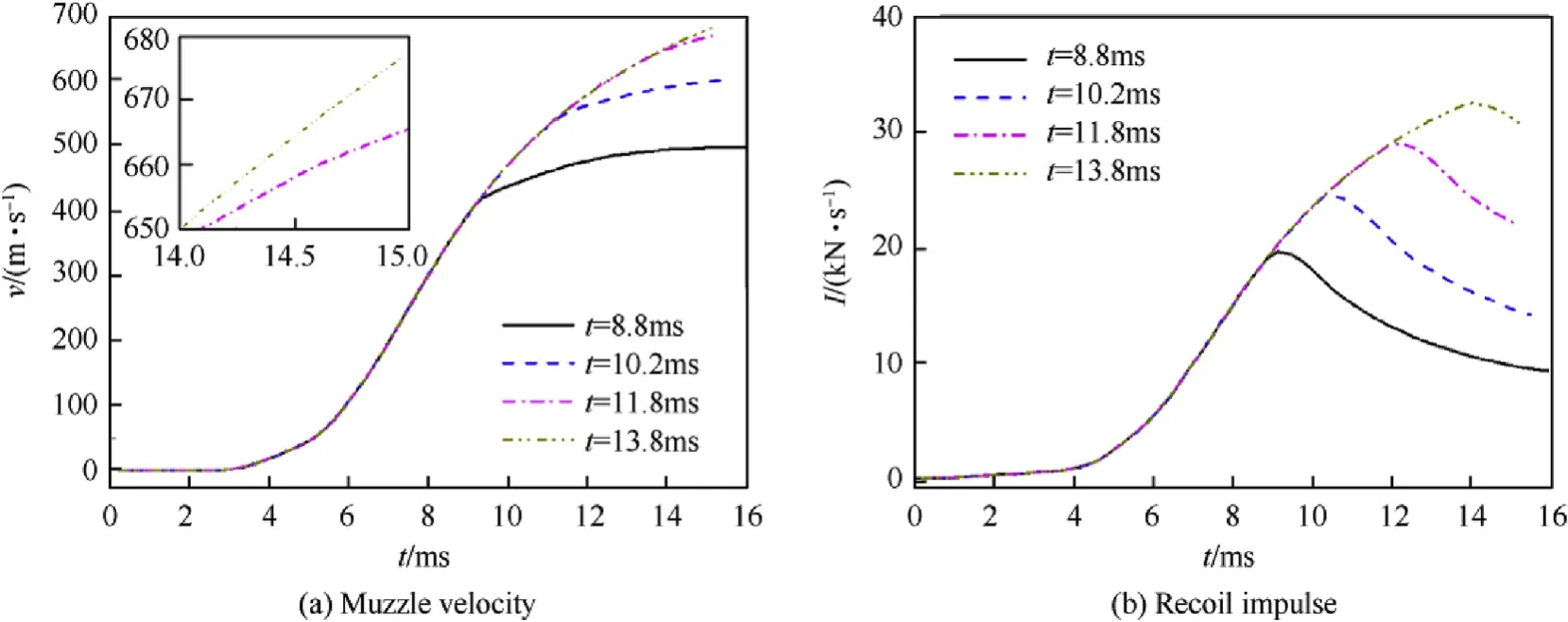
Fig.14. Time histories of ballistic characteristic at different vent opening times.
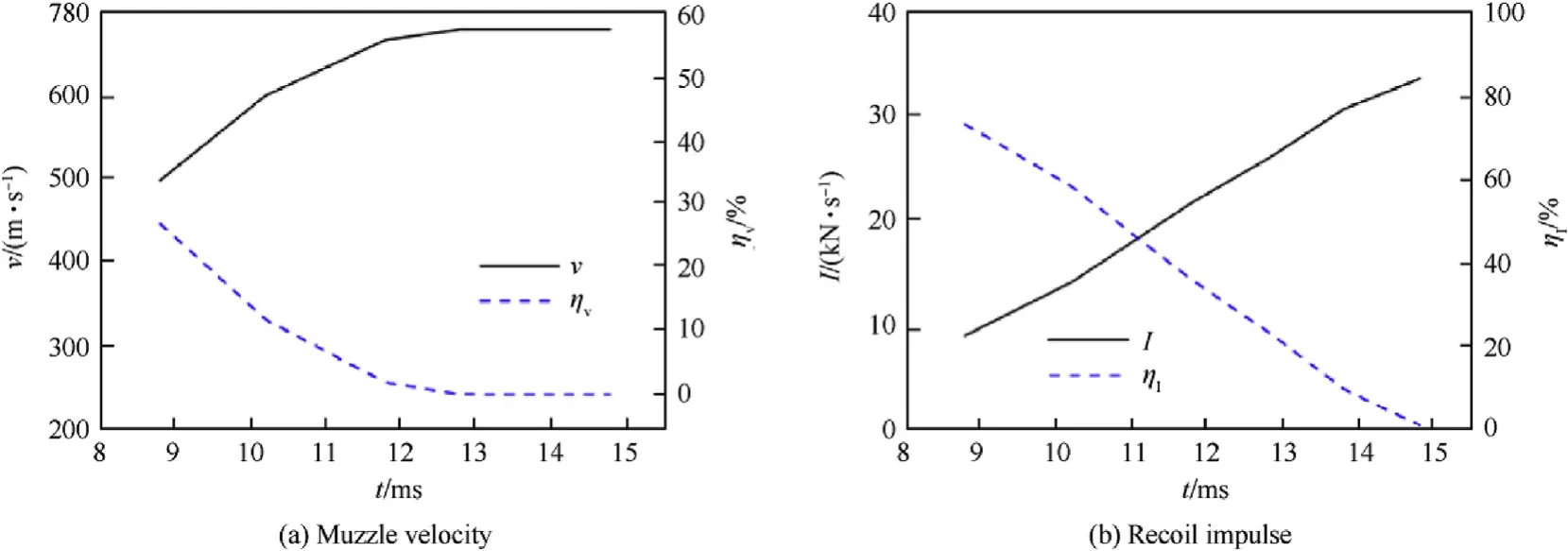
Fig.15. Ballistic characteristic and its rate of change at different vent opening times.
Through the previous discussions of two factors affecting the ballistic performance of the RAVEN with front nozzle, there are various combinations between the vent opening times and vent locations. The perfect launch performance cannot be obtained by changing one or two factors. The current predicted method is usually used to obtain the best vent opening time without muzzle velocity reduction. From the previous discussion, the current commonly used method for the prediction of the vent opening time is not particularly suitable for the RAVEN with front nozzle.Sometimes reducing the recoil impulse is a more important fact relative to the muzzle velocity. Hence, here a new predicted method is proposed based on the great number of numerical simulations. The muzzle velocity and recoil impulse can be quickly predicted by the following nonlinear fitting formulas, which are just related to the vent opening time and location.

where I is the recoil impulse, v is the muzzle velocity,t is the vent opening time, x is the distance between vent location and the breech.
Furtherly several cases were used to validate the reliability of the proposed formulas. Validation results of the new predictedmethod for different cases are shown in Table 2.vsimand Isimare the muzzle velocity and recoil impulse by the two-phase flow simulations, respectively.nd ErrI are the errors between results from the proposed formulas and the two-phase flow simulations.It is obvious that the results by the proposed formulas are very close to the results by the two-phase flow simulations.

Table 2 Validation results of the new predicted method.

Fig. 16. Time histories of projectile and rarefaction wave front position at suggested parameters.
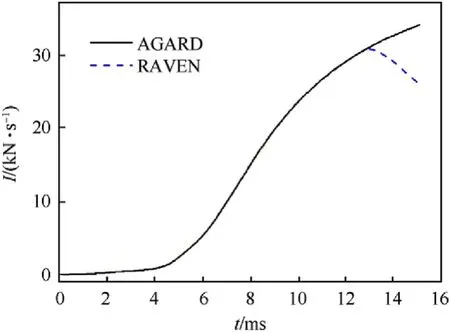
Fig. 17. Comparisons of recoil impulse between AGARD and RAVEN at suggested parameters.
The proposed formulas can be used to suggest the optimization parameters as well.Here suggested parameters are provided by the proposed formulas for the RAVEN with front nozzle in this paper.The suggested vent location is 1 m distance from the breech and the suggested vent opening time is 12.8 ms. Time histories of the projectile and rarefaction wave front position at suggested parameters are shown in Fig.16.Comparisons of the recoil impulse between the AGARD and the RAVEN at suggested parameters are shown in Fig.17. The rarefaction wave reached the projectile base when the projectile just left the muzzle. And the recoil impulse can be reduced 23.62%, almost without reducing muzzle velocity.
5. Conclusions
Numerical simulations in the RAVEN with front nozzle were carried out by using the transient two-dimensional two-fluid theory. The propellant combustion, interphase drag, intergranular stress,and heat transfer between two phases were considered in all regions of the RAVEN with front nozzle. To reduce the computational cost and improve the simulation accuracy, the arbitrary Lagrangian-Eulerian approach was used to describe the motions of the projectile. And the second-order finite volume method was implemented efficiently to describe both gas and solid phases.The main conclusions of the study are as follows:
(1) The simulation method was validated by a commonly used the AGARD gun. Comparisons of the predicted results of the AGARD gun by our code and other different codes in 參考文獻 demonstrate the accuracy and reliability of our present numerical method.
(2) Based on the condition of the AGARD gun, a RAVEN with front nozzle was proposed and numerical simulations were provided to describe and understand the physical phenomenon of the interior ballistic process in the RAVEN with front nozzle.
(3) The lower muzzle velocity and the lower recoil impulse are formed by shorter vent opening time. The rarefaction wave will reach the projectile base faster. The shorter distance between vent location and breech can increase the propagation length of the rarefaction wave. The muzzle velocity will increase and the recoil impulse will decrease.
(4) Furthermore,based on the discussions of various cases,new nonlinear fitting formulas were proposed to predict the muzzle velocity and recoil impulse. The suggested parameters were provided to make the rarefaction wave to reach the projectile base when the projectile just left the muzzle. In fact, further studies should be carried out to establish a relationship between the RAVEN performances and more parameters. This is the future direction for this work.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 11502114) and the Fundamental Research Funds for the Central Universities (Grant No.30918011323).
- Defence Technology的其它文章
- Comparative analysis of the effects of gunpowder and plasma ignition in closed vessel tests
- Numerical simulation on the pressure wave in a 30 mm electrothermal-chemical gun with the discharge rod plasma generator
- Design optimization for a launching system with novel structure
- Influence of multiple structural parameters on interior ballistics based on orthogonal test methods
- Design and manufacture of a 100 kA coaxial pulsed power cable for plasma generator and PPS in ETC guns
- Effect of the firing position on aiming error and probability of hit

