GPR Wave Propagation Model in a Complex Geoelectric Structure Using Conformal First-Order Symplectic Euler Algorithm
Man Yang,Hongyuan Fang,,Juan Zhang,Fuming Wang,Jianwei Lei and Heyang Jia
Abstract:Possessing advantages such as high computing efficiency and ease of programming,the Symplectic Euler algorithm can be applied to construct a groundpenetrating radar (GPR)wave propagation numerical model for complex geoelectric structures.However,the Symplectic Euler algorithm is still a difference algorithm,and for a complicated boundary,ladder grids are needed to perform an approximation process,which results in a certain amount of error.Further,grids that are too dense will seriously decrease computing efficiency.This paper proposes a conformal Symplectic Euler algorithm based on the conformal grid technique,amends the electric/magnetic fieldupdating equations of the Symplectic Euler algorithm by introducing the effective dielectric constant and effective permeability coefficient,and reduces the computing error caused by the ladder approximation of rectangular grids.Moreover,three surface boundary models (the underground circular void model,the undulating stratum model,and actual measurement model)are introduced.By comparing reflection waveforms simulated by the traditional Symplectic Euler algorithm,the conformal Symplectic Euler algorithm and the conformal finite difference time domain (CFDTD),the conformal Symplectic Euler algorithm achieves almost the same level of accuracy as the CFDTD method,but the conformal Symplectic Euler algorithm improves the computational efficiency compared with the CFDTD method dramatically.When the dielectric constants of the two materials vary greatly,the conformal Symplectic Euler algorithm can reduce the pseudo-waves almost by 80% compared with the traditional Symplectic Euler algorithm on average.
Keywords:Symplectic Euler algorithm,conformal grid,complex geoelectric model,ground-penetrating radar,pseudo-reflection wave.
1 Introduction
As a rapid and highly efficient underground target detection approach,ground penetrating radar (GPR)has been widely applied in the detection of structures such as roads,tunnels,and underground pipes.By establishing a GPR wave propagation numerical model for complex underground structures,GPR wave propagation can be studied,not only providing a theoretical basis for the explanation of the measured GPR signal,but also creating a precise and highly efficient forward model for the back-analysis of underground target parameters.Currently,the effect of wave focusing on displacement and pore pressure has been studied[Liu,Liang and Wu (2016)] and a fast multi-pole accelerated indirect boundary element method for broadband wave scattering has also been proposed [Liu,Sun,Cheng et al.(2018);Liu,Wang,Liang et al.(2018)].It is widely applied GPR numerical simulation approaches include the finite-difference time-domain (FDTD)approach [Bendouba,Djebli,Aid et al.(2015);Cherief,Elmeguenni and Benguediab (2016);Choudhury and Jha (2013)]the alternating direction implicit FDTD (ADI-FDTD)approach [Datta and Ray (2015);Dincel and Akbarov (2017);Dong,El-Gizawy,Juhany et al.(2014);Dong,Haynes and Atluri (2015);Essam,Mhamed and Thamar (2015)],and finite element analysis [Fan,Zhang,Dong et al.(2015);Khellafi,Meddah,Chikh et al.(2015);Lam and Pan (2015);Liu,Zhang and Xia (2017);Ma,Sato and Takada (2015);Miao,Chen and Wang (2014)].Ghasemi et al.[Ghasemi,Park and Rabczuk (2018)] have proposed a method for calculating the topological optimization of a multi-material flexible electric composite material,and the obtained design sensitivity is applied to the Hamilton-Jacobi (H-J)equation,and the LS function is modified.Ghasemi et al.[Ghasemi,Park and Rabczuk (2017)] have provided numerical examples showing that topology optimization can improve mechatronic coupling coefficient significantly.Nanthakumar et al.[Nanthakumar,Lahmer,Zhuang et al.(2016)] have proposed a method to solve the inverse problem of interface detection of inclusions in piezoelectric structures.Yakhno et al.[Yakhno and Cicek (2014)] have come up with approximate calculation method of electromagnetic Green's function for time Harmonic Maxwell equations for an approximate General Electrorotational anisotropic Materials.
The Symplectic Euler algorithm is a time-domain electromagnetic field numerical computing method proposed in recent years that maintains a constant overall energy of the Hamilton system,has the advantage that only two functions are needed to fully describe the electromagnetic field in the two-dimensional case.Although the propagation of GPR waves in pavement structure cannot be regarded as a classical Hamiltonian system due to the energy dissipation of pavement materials,the Symplectic Euler algorithm is still applicable [Fang and Lin (2012)].With respect to the classic time-domain finite difference method,this reduces computing time by 25% without sacrificing computing precision[Fang and Lin (2012);Fang,Lin and Zhang (2013)].Anitescu et al.[Anitescu,Jia,Zhang et al.(2015)] have developed improvement of Gilleville abscess with external point collocation.However,the Symplectic Euler algorithm is still a difference algorithm.When using rectangular grids to perform two-dimensional spatial dispersion for a complex underground target,the grids need to be encrypted in order to precisely simulate the surface boundary,and are subject to the Courant-Friedrichs-Levy (CFL)stability condition.Thus,grids that are too dense will greatly lower the computing efficiency [Chen,Stang and Moghaddam (2016);Feng and Dai (2011);Gao and Zhai (2017);Ghasemi and Abrishamian (2007)].
To improve computing precision and efficiency when modeling complex underground targets,approaches such as the sub-grid technique [Berenger (2005);Diamanti and Giannopoulos (2009);Georgakopoulos,Birtcher and Balanis (2002)] and the grid-free method [Feng,Guo and Wang,(2015)] have been utilized.The sub-grid technique uses relatively fine grids at the surface boundary and relatively coarse grids in other regions,thus shortening the computing time.Singular boundary method [Tang,Fu,Zheng et al.(2018)] and singular boundary method [Fu,Chen,Chen et al.(2014);Fu,Chen,Wen et al.(2018)] for wave propagation analysis in periodic structures has been used in periodic structures and the SBM has been used to solve the infinite domain problems.This approach,however,leads to pseudo-reflection waves at the interface between the coarse and fine grids.The grid-free approach relies on the moving least squares (MLS)method to fit the field function.Although it eliminates the constraints on the units,it is relatively difficult to establish near-field functionality when the geoelectric structure is complex.
The conformal grid technique is a parameter processing method that processes grids at the medium interface where one grid contains several media.Recently,Hamdia et al.[Hamdia,Ghasemi,Zhuang et al.(2018);Hamdia,Silani,Zhuang et al.(2017)] have applied sensitivity analysis to determine the key input parameters affecting the energy conversion coefficient(ecf)of flexible materials.Vu-Bac et al.[Vu-Bac,Lahmer,Zhuang et al.(2016)] have provided a sensitivity analysis toolbox consisting of a set of Matlab functions.During the numerical computing process,the grid density is not increased,the size of the local grids of the model is not altered,and the effective amendment of the medium parameter is only performed on grids containing non-uniform medium [Dai,Wang,Feng et al.(2012);Feng and Dai (2011);Fang and Lin (2013);Feng and Dai (2010);Guo,Chen and Xu (2017)].This method is easy to derive and program,and has been applied in the processing of electromagnetic signals on the surfaces of invisible airplanes and invisible clothing,as well as in the optimization of various antenna designs by the military [Dai,Feng,Wang et al.(2004);Uduwawala (2006);Yang,Li,Cheng et al.(2018);Zhong,Zhang and Xie (2011)].Using two-dimensional transverse magnetic (TM)waves as an example,this study combines the conformal grid technique and the Symplectic Euler algorithm to establish a forward numerical model for the wave propagation of GPR electromagnetic wave in a complex geoelectric structure,where transmitting boundary conditions are applied.Using the underground circular void and undulating stratum models,the computing precision of the conformal Symplectic Euler algorithm is validated.The conformal Symplectic Euler algorithm have almost the same level of accuracy as the CFDTD method,the conformal Symplectic Euler algorithm dramatically improves the computational efficiency compared with the CFDTD and when the dielectric constants of the two materials vary greatly,conformal Symplectic Euler algorithm can reduce the pseudo-waves almost by 80%compared with the traditional Symplectic Euler algorithm on average.This paper adopts matlab R 2014a software for numerical simulation.
2 Symplectic Euler algorithm
2.1 Expression of the Symplectic Euler algorithm
We let Ωto be a domain (i.e.,a non-empty,open,simply connected set)in the oriented Euclidean spaceR2nof the pointHis a sufficiently smooth real function defined inΩ,then the n-dimensional Hamilton system can be expressed as[ Sun (1995);Huang and Wu (2006)]:

For a special type of Hamilton system,i.e.,the divisional Hamilton system,the Hamilton function can be expressed as

where H(p,q)denotes the Hamiltonian functions,V(q)and U(p)represent two directional components ofH(p,q).
Eq.(1)can be simplified as

The above equations are ordinary differential equations,which are often solved using the Runge-Kutta methods.Assuming Eq.(3)is solved by a Runge-Kutta method,and Eq.(4)is solved by another Runge-Kutta method,such a computing technique may be classified as a partitioned Runge-Kutta method.Each L-stage partitioned Runge-Kutta method can have an independent Butcher expression.
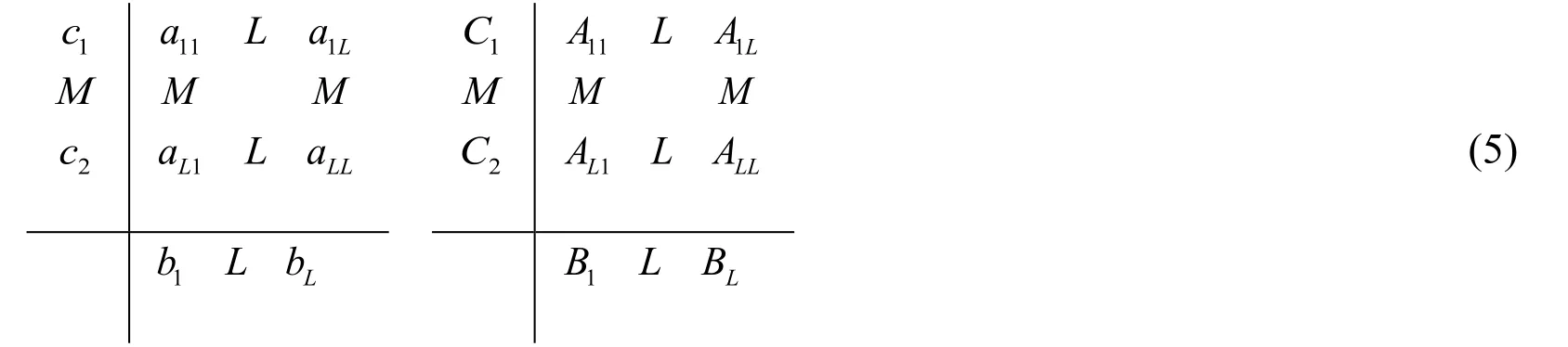
Substituting Eq.(5)into Eq.(3)and Eq.(4)yields

whereτis time increment.If the coefficients of the Eq.(6)satisfy

The Butcher expression is Symplectic,and the Butcher expression of the first-order Symplectic Euler method is as follows.

Major reasons to use this method include:(1)Among the single-step Symplectic algorithms belonging to the same order,it requires the least amount of computation;(2)For the damping system,it is still in an explicit format.
2.2 The iterative format of the Symplectic Euler algorithm
In isotropic media,the differentiation formats of the time-domain Maxwell equations are expressed as

The constitutive relation is

where D represents the dielectric flux density,B represents the magnetic flux density,E and Hrepresent the vectors for electric field and magnetic field,respectively,Jis the current density,andε,μandσrepresent the relative dielectric constant,the relative permeability,and the relative conductivity,respectively.Because the medium is isotropic,ε,μ,andσare all constants.Substituting Eq.(11)into Eq.(9)and Eq.(10)yields


By letting the magnetic vector potential H = ?×A,and E = -U,A andUrepresent the vectors for electric field and magnetic field,respectively,the general Hamilton function in the lossy system can be expressed as
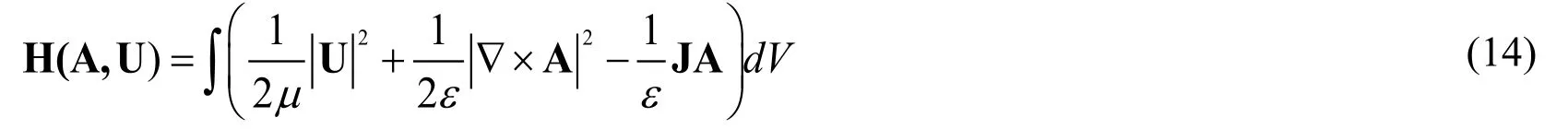
By combining Eq.(14)with Eq.(3)and Eq.(4),we obtain

When only considering TM waves,Eq.(15)and Eq.(16)can be simplified as

In these equations.,AzandUzrepresent the vector components of the fields A and U along the directionZ,where ?2is the Laplace operator.
Substituting Eq.(8)into Eq.(17)and Eq.(18)yields:

From the above,the iterative formats of the first-order Symplectic Euler method are found to be

From Eq.(23)and Eq.(24),the differential iterative equations of the first-order Symplectic Euler algorithm become
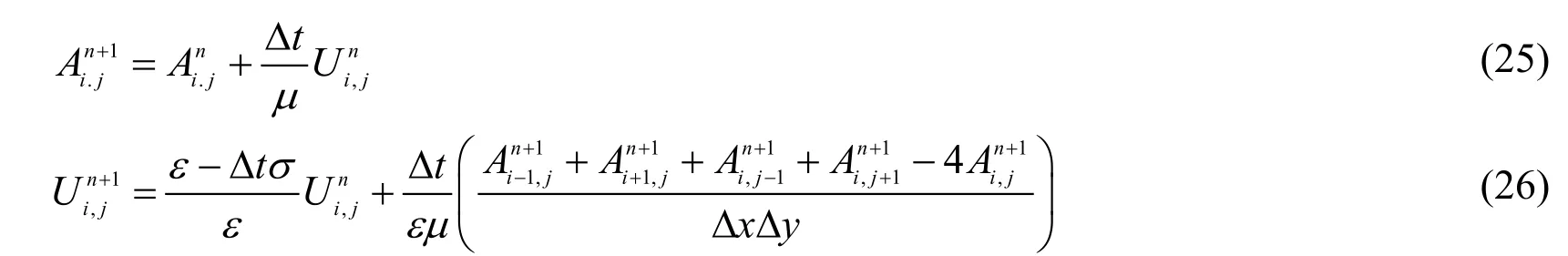
In the equation,Δxand Δyrepresent the grid lengths along directionxand directiony,respectively.
The components of the electric and magnetic fieldsEZ,Hx,andHyare defined in Eq.27.

2.3 The iterative format of the conformal Symplectic Euler method
Using the two-dimensional quadrangle as an example,in Fig.1,Fig.1(a)is the actual subdivision diagram of the model grids,Fig.1(b)is a subdivision diagram of the conventional ladder approximation,and Fig.1(c)is the processing subdivision diagram of the conformal grids.In particular,grids that are entirely inside the quadrangle or entirely outside of the quadrangle are classified as normal grids,while the remainder are classified as conformal grids.The conformal grids are processed using the effective medium parameters,while the non-conformal grids are processed in the staircase way.
Using TM waves as an example,a cell is extracted from Fig.1(c)to illustrate the equivalent parameter processing of the conformal grids.
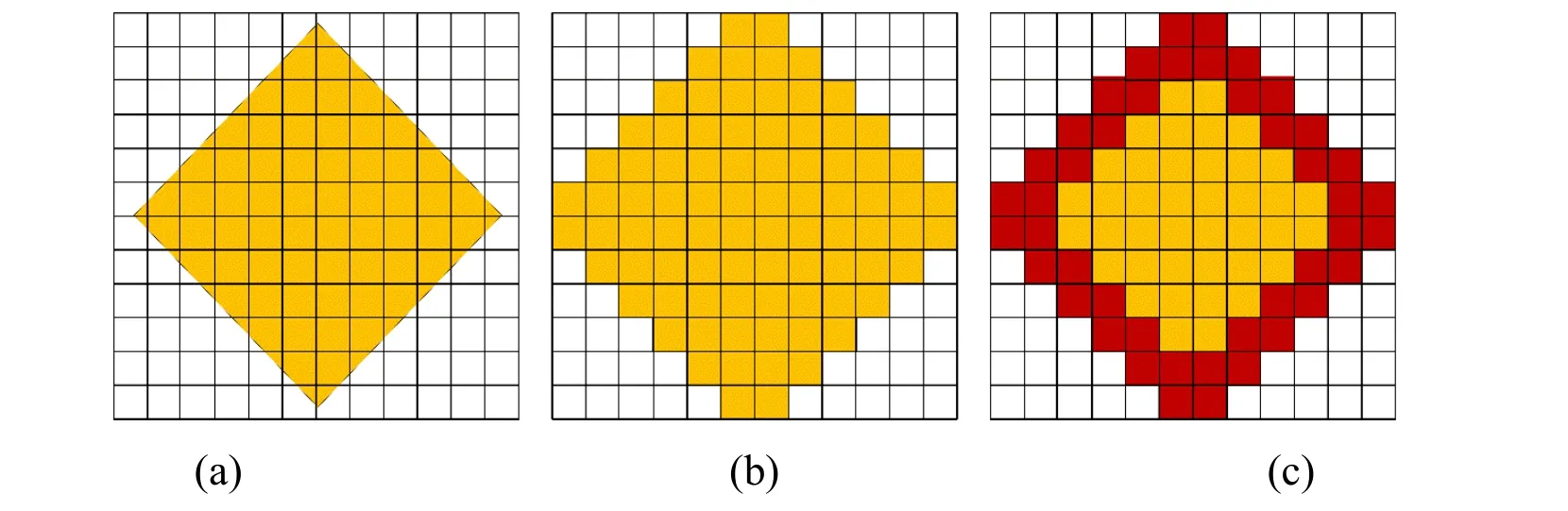
Figure1:Schematic view for subdivisions.(a)Actual model grids,(b)Conventional ladder approximation,(c)Conformal grids
In the Symplectic method,the field componentsUand Aare defined at the same spatial grid nodes and the same time steps.Sxy1andSxy2represents the area of medium 1 and medium 2,respectively.The calculation of the conformal grids of the medium in orthogonal coordinates is shown in Fig.2,whereFis the sampling point of the field components U and A.We assume that the electromagnetic parameters of medium 1 areε1,σ1,μ1,andσm1,and the electromagnetic parameters of medium 2 areε2,σ2,μ2,andσm2.From Fig.2,it can be seen that the field components U and A are located at the center of the grids.Therefore,the effective values of the dielectric constant,the conductivity,the permeability coefficient,and the permeability can be obtained by weighted averaging of the areas on adjacent surfaces occupied by different media.

Figure2:Equivalence of the medium parameters in conformal grids.(a)Before equivalence,(b)After equivalence
The equivalent dielectric constant,the equivalent conductivity,the equivalent permeability coefficient,and the equivalent permeability,at sampling point F of the field component in Fig.2 are as follows:

whereeffdenotes equivalent.
Substituting Eq.(28),Eq.(29),Eq.(30)and Eq.(31)into Eq.(25)and Eq.(26),we obtain the differential iterative equations for the first-order conformal Symplectic Euler method.However,the conformal Symplectic Euler algorithm can deal with the medium in this paper at present,and when the material is metallic conductor,we need special treatment of the Eq.(32)and Eq.(33).
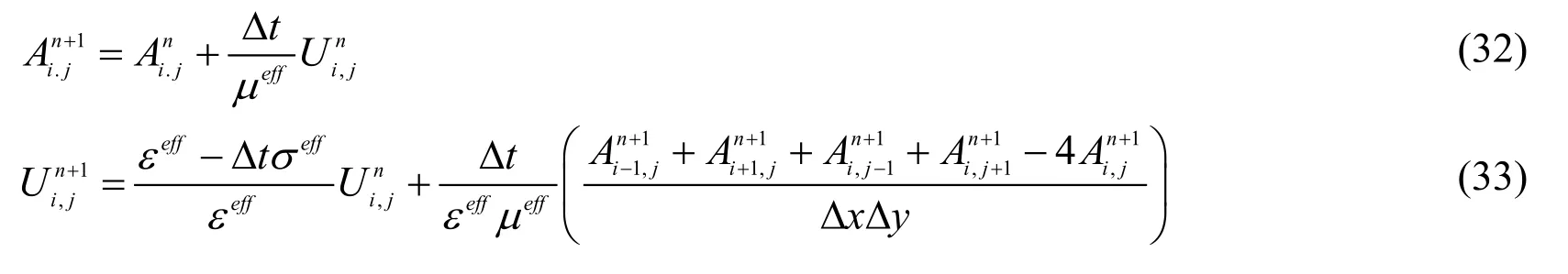
3 Numerical stability
In order to ensure the computational stability of the conformal Symplectic Euler algorithm,the selection of space interval and time step of the conformal Symplectic Euler algorithm also needs to meet the stability conditions requirement.In this paper,the stability of Symplectic computation was analyzed by the amplification matrix method.It is assumed that all materials are loss-free.The two-dimensional line wave source can be expressed as Eq.(34)[Fang,Lin and Zhang (2013)].

Eq.(33)can be expressed as
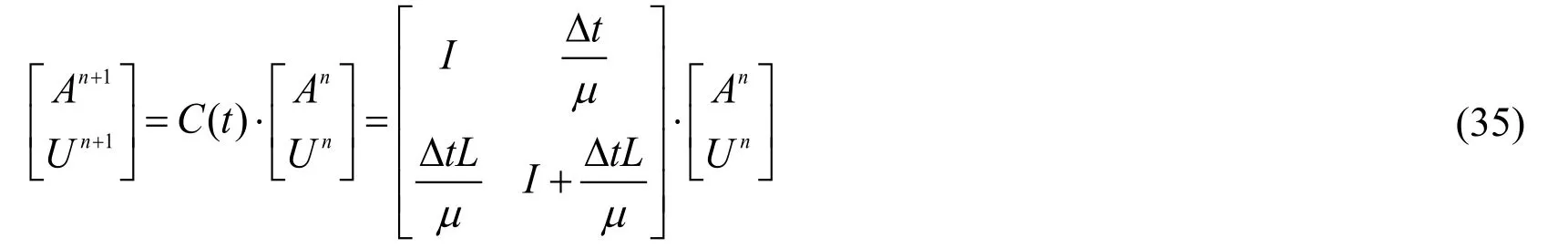
whereC(t)defines the amplification matrix,Substitute Eq.(34)into Laplace operator and then carry out difference discretization to obtain Eq.(36).

The characteristic equation of the amplification matrix can be shown in Eq.(37).

when the absolute value of all eigenvalues of the characteristic Eq.(37)are less than or equal to unity “1”,the conformal Symplectic Euler algorithm is stable.
Therefore,if Δx= Δy=δand the two-dimensional stability condition of the first-order conformal Symplectic Euler algorithm can be expressed as Eq.(38):

Wherecis velocity of light.
4 Transmitting boundary conditions
4.1 Differential equations
The key function of the transmitting boundaries [Liao (1996);Liao,Wong,Yang et al.(1984)] is to represent the one-way fluctuation of any point that propagates outwards along the normal direction at the cut-off boundary of the computing region as the superposition of a series of outgoing plane waves.

wherefn(cnt-x)represents thenth one-way fluctuation propagating along thex-axis,andcnrepresents the apparent velocity.Eq.(39)is one-dimensional,but the one-side fluctuation can be two-dimensional as well as three-dimensional.It can also be the ordinary expression of any linear one-side fluctuation.In recent years,because the precision of the equation is controllable and the programming is straightforward,it has been widely applied to numerical simulation issues in various types of engineering fluctuations.
As shown in Fig.3,the N-order transmitting boundary condition equation (MTF)at the left cut-off boundary is expressed as

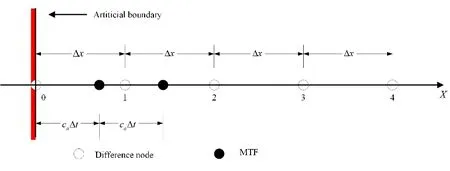
Figure3:Schematic view of the MTF computing points and spatial grid nodes at the leftside boundary
This paper adopts the second-order transmitting boundary,i.e.,

From Fig.3,it can be seen that the spatial grid nodejΔxdoes not need to coincide with the pointjcΔx.Differential calculation is performed onusing the field values at theaspatial grid node.ThenΔtmoment is defined,and the field value at the spatial grid nodejΔxis

First,the field values at pointsx=0,x= Δx,andx= 2Δxat the momentnΔtundergo secondary differentiation,to obtain the field valueU1nat the pointx=caΔtat the momentnΔt.

whereN1,1= (2 -s)(1 -s)/2,N1,2=s(2 -s),N1,3=s(s-1)/2ands=caΔt/ Δx.
Similarly,differentiation is performed onto obtain

Similar calculations can be performed on other boundaries.
4.2 Validation of the boundary conditions
A 2m× 2mmodel is selected,where the excitation signal source is located at its center,the Ricker sub-waves with an antenna frequency of 1 GHz are applied,the time step is selected to be 0.01 ns,and the spatial step length is selected to be 0.005 m.The computing region is filled with air,which has a relative dielectric constant of 1 and relative conductivity of 0 mS/m.The model and the absorption effects are shown in Fig.4.

Figure4:Validation of the adsorption effects in the uniform medium.(a)Snapshot of the wave field at 2.5 ns,(b)Snapshot of the wave field at 5 ns,(c)Snapshot of the wave field at 7.5 ns,(d)Snapshot of the wave field at 10 ns
From Fig.4,it can be seen that the absorption effects under the transmitting boundary conditions are satisfied,and there are no apparent reflection waves at the boundaries.
5 Numerical simulations
5.1 Example 1
The schematic view of the model is illustrated in Fig.5,where the media in the model consist of two layers [ Hamdia,Ghasemi,Zhuang et al.(2018);Hamdia,Silani,Zhuang et al.(2017);Fang,Lin and Zhang (2013);Vu-Bac,Lahmer,Zhuang et al.(2016)]:the first layer is air,with a relative dielectric constantε0of 1 and a conductivityσ0of 0;the second layer has a relative dielectric constantε1of 6 and conductivityσ1of 1 mS/m.Further,a circular void with a diameter of 15 cm is introduced into the second layer,in which the location of the circular center is (1 m,0.5 m).By varying the dielectric constant of the circular void medium,the impacts of conformal grid and non-conformal grid processing on the GPR signals in media with different dielectric constants can be analyzed.The relative dielectric constants of media in the circular void are designed to be 1,3,6.4,10,16,and 20.All media are assumed to be non-magnetic;in other words,we assume that their relative permeabilityμis 1.Each time step is 0.01 ns,the spacing between each spatial grid is 0.005 m,the total number of simulated time steps is 5000,the Ricker subwaves with frequency 1 GHz are selected at the center of the transmitting antenna,the reflection waves are received atx= 1m,and the distance from the transmitting location to the ground is 1 grid.We have used the same parameters between the CFDTD method and the conformal Symplectic Euler Algorithm.Fig.6 shows the comparison between conformal Symplectic Euler algorithm and CFDTD reflection waves (the relative dielectric constant of the circular void portion is 3).Fig.7 shows the absolute error of the amplitude of the reflection waves by the CFDTD method and the conformal Symplectic Euler algorithm (the relative dielectric constant of the circular void portion is 3).Fig.8 shows the relative error of the amplitude of the reflection waves by the CFDTD method and the conformal Symplectic Euler algorithm (the relative dielectric constant of the circular void portion is 3).The reflection waveforms in the simulated computation are shown in Figs.9,10,11,12,13 and 14.
Fig.7 and Fig.8 give the quantitative comparison of the difference in amplitude of the two methods.The maximum absolute difference between the two methods is no more than 0.00002 V/m,and the maximum relative difference between the two methods is 14.8%,the average relative difference between the two methods is 2.9%,the relative difference equals 0.00015% for the first peak at 0.81 ns,0.079% for the secondary peak at 3.26 ns and 0.1% for the third peak at 5.86 ns,and in short,95% of the relative error is within plus or minus 5%.Based on comparison Fig.6 and Fig.7,we can obtain the accuracy of the two algorithms is the same,but the computational time of the conformal Symplectic Euler algorithm is 3.99 s,and the other computational time of the CFDTD method is 5.32 s.In conclusion,the conformal Symplectic Euler algorithm greatly improves the computational efficiency[Anitescu,Jia,Zhang et al.(2015)] compared with the CFDTD method.
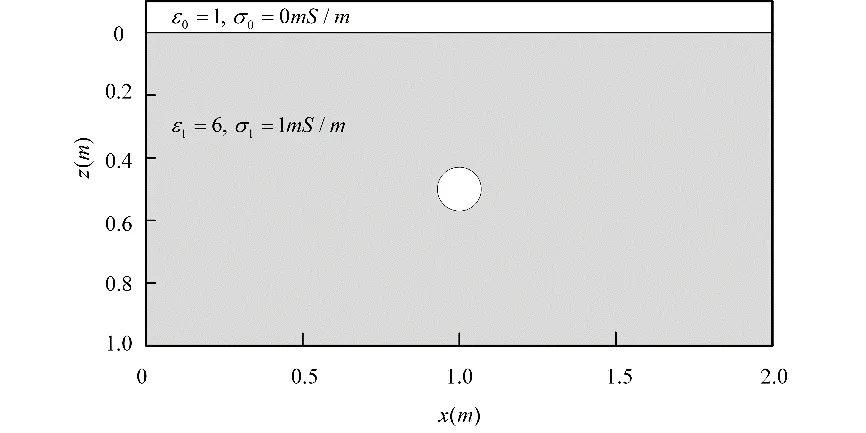
Figure5:Schematic view of the circular void model

Figure6:Comparison between conformal Symplectic Euler algorithm and CFDTD reflection waves (the relative dielectric constant of the circular void portion is 3)
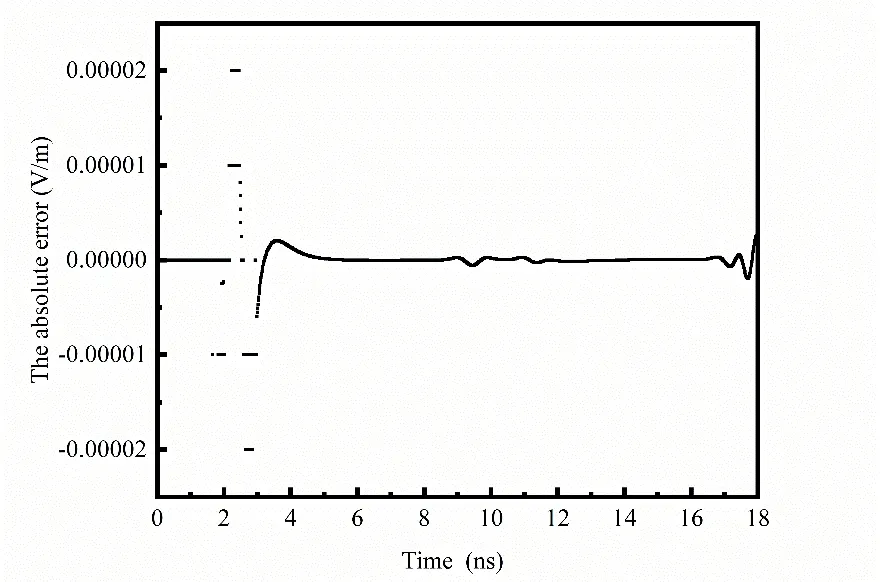
Figure7:Absolute error of the amplitude of the reflection waves by the CFDTD method and the conformal Symplectic Euler algorithm (the relative dielectric constant of the circular void portion is 3)
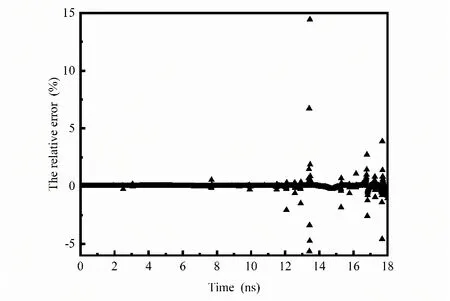
Figure8:The relative error of the amplitude of the reflection waves by the CFDTD method and the conformal Symplectic Euler algorithm (the relative dielectric constant of the circular void portion is 3)
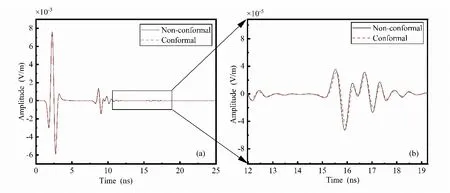
Figure9:Comparison between conformal and non-conformal Symplectic Euler algorithm reflection waves (the relative dielectric constant of circular void portion is 1)
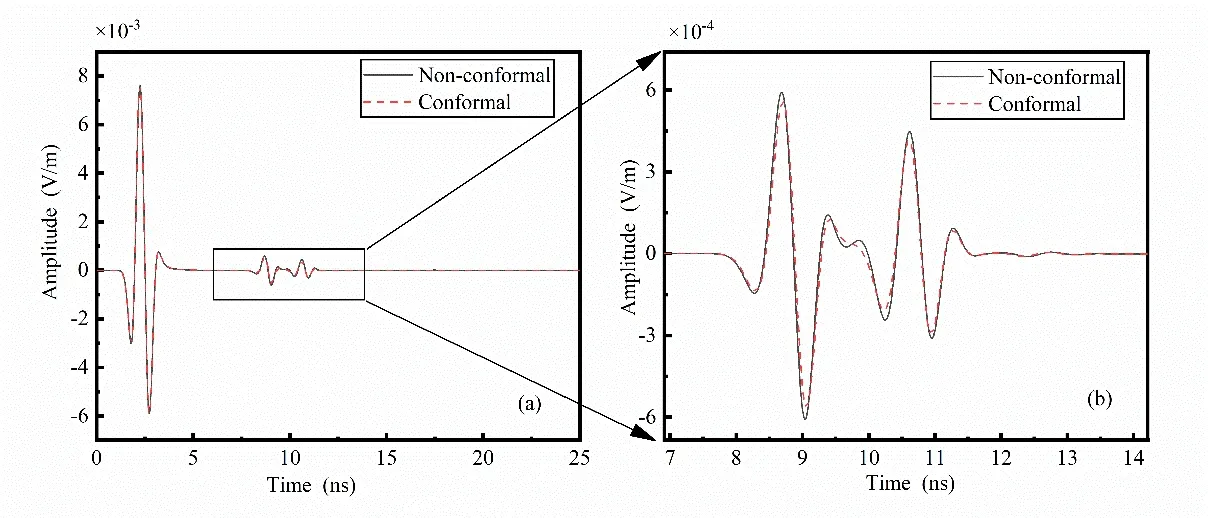
Figure10:Comparison between conformal and non-conformal Symplectic Euler algorithm reflection waves (the relative dielectric constant of circular void portion is 3)

Figure11:Comparison between conformal and non-conformal Symplectic Euler algorithm reflection waves (the relative dielectric constant of circular void portion is 6.4)
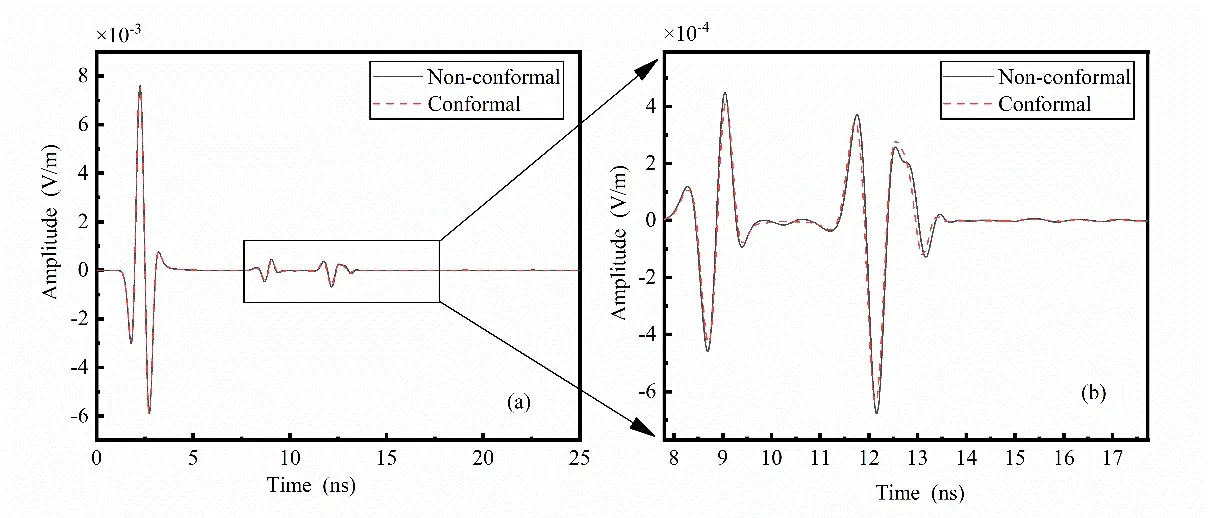
Figure12:Comparison between conformal and non-conformal Symplectic Euler algorithm reflection waves (the relative dielectric constant of circular void portion is 10)
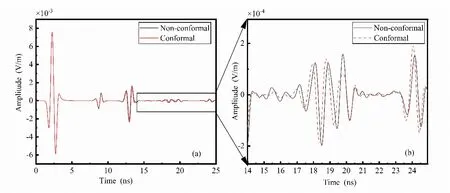
Figure13:Comparison between conformal and non-conformal Symplectic Euler algorithm reflection waves (the relative dielectric constant of circular void portion is 16)
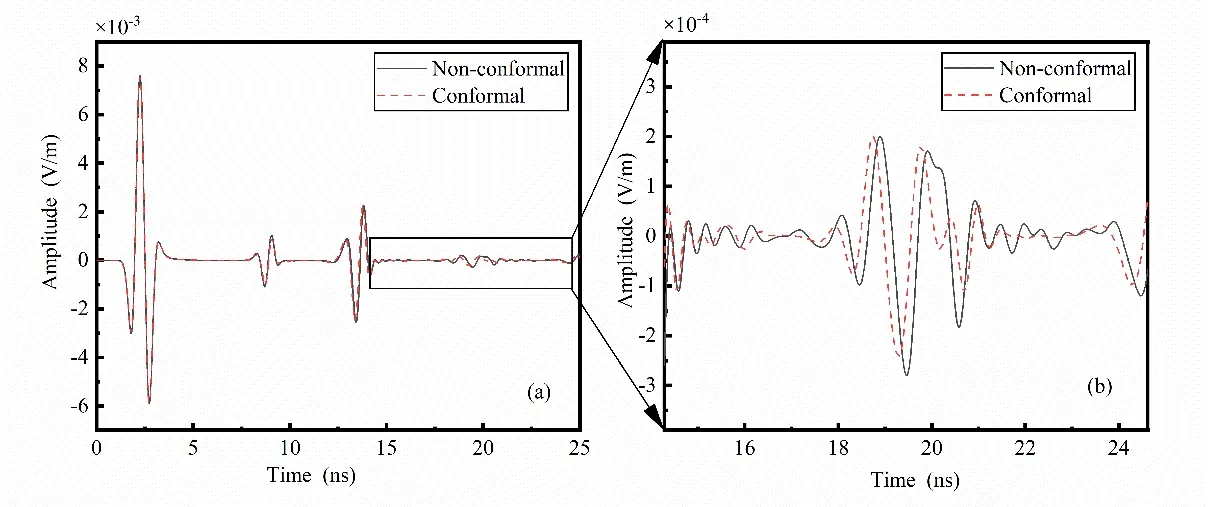
Figure14:Comparison between conformal and non-conformal Symplectic Euler algorithm reflection waves (the relative dielectric constant of circular void portion is 20)
From Figs.9-14,it can be seen that the greater the difference between the dielectric constant of the material filling the circular void portion and that of the medium of the second layer,the more diffracted waves are generated by non-conformal processing.Fig.14 shows the comparison between conformal and non-conformal Symplectic Euler algorithm reflection waves (the relative dielectric constant of the circular void portion is 20).Fig.14(b)shows the amplitude of the virtual wave was reduced by 96.18% for the first peak at 19.77 ns,59.51% for the second peak at 21.31 ns and 87.35% for the third peak at 22.54 ns.On average,80% of the diffraction wave can be eliminated by the conformal Symplectic Euler algorithm.
Therefore,it is concluded that conformal processing can effectively remove artificial waves generated by the ladder approximation approach.The greater relative difference between the dielectric constants of the two materials,the more necessary to adopt the conformal Symplectic Euler algorithm.
5.2 Example 2
An undulating geoelectric model is selected,as shown in Fig.15.The first layer is air,with a relative dielectric constantε0of 1 and conductivityσ0of 0 mS/m [Hamdia,Ghasemi,Zhuang et al.(2018);Hamdia,Silani,Zhuang et al.(2017);Fang,Lin and Zhang (2013);Vu-Bac,Lahmer,Zhuang et al.(2016)];the second layer has a relative dielectric constantε1of 6 and conductivityσ1of 1 mS/m;the third layer has a relative dielectric constantε2of 14 and conductivityσ2of 2 mS/m.The entire computing area has a size of 20m× 10m.We assume all media are non-magnetic,i.e.,their relative permeabilityμis 1,and the spacing between spatial grids is selected to be 0.05 m.The manners of self-excitation and self-receiving are applied,and synchronous movement is performed from left to right,in which the time step is 0.1 ns,the total number of simulated time steps is 3000,and the Ricker sub-waves with a frequency of 100 MHz are selected at the excitation source center,whose location is 1 grid away from the ground surface.Figs.15,16 and 17 are comparison and wiggle diagrams of the reflection waveforms obtained by conformal and nonconformal Symplectic Euler algorithm grid processing.

Figure15:Schematic view of the undulating geoelectric model
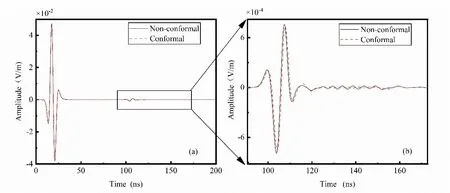
Figure16:Comparison diagram of reflection waves between conformal and nonconformal Symplectic Euler algorithm grid processing

Figure17:Subdivision diagram of the GPR by the non-conformal Symplectic Euler algorithm
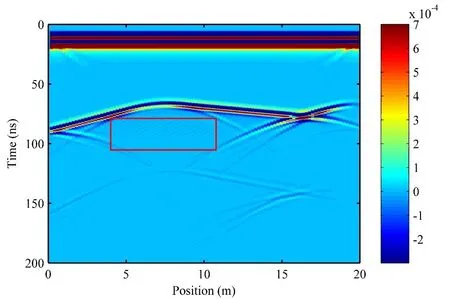
Figure18:Subdivision diagram of the GPR by the conformal Symplectic Euler algorithm
From Figs.16,17 and 18,it can be seen that,in comparison to the conventional Symplectic Euler algorithm,the conformal Symplectic Euler algorithm greatly reduces the pseudowaves generated by the ladder approximation (see red box in Fig.17 and Fig.18).
5.3 Example 3
In order to verify the effect of the example 1 and example 2,in the laboratory we dug a 1m×1m×1msquare hole filled with dry sand,and a plastic pipe was buried at a depth of 15.2 cm.The center frequency of the ground penetrating radar (GPR)is 2.5 GHz,the number of sampling points is 512,the time window is 12 ns,and the antenna movement step is 0.004 m.The GPR measures along the dotted line.Fig.19 shows the diagram the GPR measurement schematic.Fig.20 shows the comparison diagram of the single-channel wave of the actual value of the radar measurement and the simulated value.
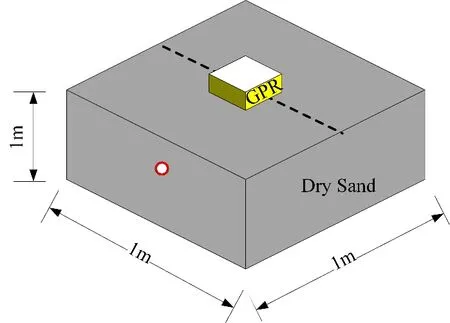
Figure19:The diagram the GPR measurement schematic
It can be seen from Fig.20 that the actual measured data are basically consistent with the conformal Symplectic Euler algorithm and the CFDTD method,indicating that the accuracy and error of the conformal Symplectic Euler algorithm are small,and this algorithm is effective in reducing the diffraction wave in GPR imaging.In Fig.20,the computational time of the conformal Symplectic Euler algorithm is 1.22 s,and the other computational time of the CFDTD method is 1.89 s.In short,the conformal Symplectic Euler algorithm greatly improves the computational efficiency compared with the CFDTD method.
6 Conclusions
This study combined the conformal grid technique and the Symplectic Euler algorithm,established a numerical model illustrating the wave propagation of GPR electromagnetic in a complex geoelectric structure,validated the adsorption effects under the transmitting boundary conditions,and compared the reflection waveforms simulated by conformal and non-conformal processing for the circular void and undulating stratum models,and compared with the actual measurement data and conformal Symplectic Euler algorithm.The conformal Symplectic Euler algorithm achieves almost the same level of accuracy as the CFDTD method,but the conformal Symplectic Euler algorithm improves the computational efficiency enormously compared with the CFDTD method.When the dielectric constants of the two materials vary greatly,conformal Symplectic Euler algorithm can reduce the pseudo-waves almost by 80% compared with the traditional Symplectic Euler algorithm.The results indicate that the conformal Symplectic Euler algorithm can effectively reduce pseudo-reflection waves and decrease the error brought about by the ladder approximation at the surface boundary of the underground structure.The further theoretical study of conformal symplectic Euler algorithm and the application of more interesting engineering problems including conductor materials are still the research topics in the future.
Acknowledgments:This research was funded by the National Key Research and Development Program of China (No.2017YFC1501204),the National Natural Science Foundation of China (Nos.51678536,41404096),the Scientific and Technological Research Program of Henan Province (No.171100310100),Program for Innovative Research Team (in Science and Technology)in University of Henan Province(19HASTIT043),the Outstanding Young Talent Research Fund of Zhengzhou University(1621323001).
 Computers Materials&Continua2019年11期
Computers Materials&Continua2019年11期
- Computers Materials&Continua的其它文章
- Efficient Computation Offloading in Mobile Cloud Computing for Video Streaming Over 5G
- Geek Talents:Who are the Top Experts on GitHub and Stack Overflow?
- Implementing the Node Based Smoothed Finite Element Method as User Element in Abaqus for Linear and Nonlinear Elasticity
- Dynamics of the Moving Ring Load Acting in the System“Hollow Cylinder + Surrounding Medium” with Inhomogeneous Initial Stresses
- Human Behavior Classification Using Geometrical Features of Skeleton and Support Vector Machines
- Improvement of Flat Surfaces Quality of Aluminum Alloy 6061-O By A Proposed Trajectory of Ball Burnishing Tool
