Measure-Resend Semi-Quantum Private Comparison Scheme Using GHZ Class States
Lili Yan,Yan ChangShibin ZhangQirun Wang,Zhiwei Sheng and Yuhua Sun
Abstract:Quantum private comparison is an important topic in quantum cryptography.Recently,the idea of semi-quantumness has been often used in designing private comparison protocol,which allows some of the participants to remain classical.In this paper,we propose a semi quantum private comparison scheme based on Greenberge-Horne-Zeilinger (GHZ)class states,which allows two classical participants to compare the equality of their private secret with the help of a quantum third party (server).In the proposed protocol,server is semi-honest who will follow the protocol honestly,but he may try to learn additional information from the protocol execution.The classical participants’ activi ties are restricted to either measuring a quantum state or reflecting it in the classical basis In addition,security and efficiency of the proposed schemes have been discussed.
Keywords:Quantum private comparison,semi-quantum protocol,semi-honest third party,GHZ class states.
1 Introduction
Since Bennett and Brassard proposed the first quantum key distribution (QKD)protocol[Bennett and Brassard (1984)],various facets of secure communication have been explored using quantum technology,such as QKD [Ekert (1991);Bennett (1992)],Quantum secret sharing (QSS)[Long and Liu (2002);Guo (2002);Karlsson,Koashi and Imoto (1999)],Quantum secure direct communication (QSDC)[Deng,Gui and Liu(2003);Deng and Gui (2004);Zhong,Liu and Xu (2018);Man and Xia (2004)] and quantum private comparison (QPC).The main goal of QPCs is to compare the equality of parties’ private information in pubic without revealing their information.The first QPC protocol was proposed by Yang et al.[Yang and Wen (2009)] using Einstein-Podolsky-Rosen (EPR)pairs.Many QPC protocol have been proposed with different quantum states in recent years,such as single particles [Yang,Gao and Wen (2009);Chen,Su,Niu et al.(2014);Liu,Gao,Jia et al.(2013);Yang,Xia,Jia et al.(2012)],Bell states [Yang and Wen (2009);Liu,Wang and Cui (2012);Tseng,Lin and Hwang (2012);Wang,Xu and Yang (2013);Lin,Yang and Hwang (2014)],GHZ states [Chen,Xu,Niu et al.(2010);Liu and Wang (2012);Chang,Tsai and Hwang (2013)] and multiple particle state.A pioneering work of Lo [Lo(2007)] pointed out two-party secure QPC is not possible.This implies that to implement secure QPC,we must have a third party,who would assist the users to compare the equality of their secrets.
It is easy to find out that all above QPC protocols require all the participants to have quantum capabilities.That is,all the participants equip advance quantum devices such as qubit generating devices and quantum memory,unitary operation and so on.So,how much quantumness is needed for participants? Alternatively,whether all the participants are required to have quantum capabilities? However,such expensive quantum resources and operations cannot be afforded by all parties.In this case,it will be difficult to apply these protocols in real environments.In 2007,Boyer et al.[Boyer,Kenigsberg and Mor(2007)] proposed the first semi-quantum key distribution.There are two participants in Boyer et al.’s schemes.One is a powerful quantum operator and the other one has only classical capabilities.The classic party can either reflect the qubits without disturbed or perform measurement and prepare a new qubit in the classical basis {0,1}.In Boyer’s protocol,it assumes that the classical party has access to a segment of the quantum channel that leads from the lab of the powerful quantum operator to the outside world and then goes back.
Soon after,many researches based on the semi-quantum have been proposed,such as semi-quantum secret sharing (SQSS),semi-quantum key distribution (SQKD),semiquantum secure direct communication (SQSDC)and semi-quantum private comparison(SQPC).Recently,Chou et al.[Chou,Hwang and Gu (2016)]put forward a SQPC protocol based on Bell states.But the protocol employs quantum entanglement swapping.Thapliyala et al.[Thapliyala,Sharmab and Pathak (2016)] proposed a SQPC protocol using Bell entangled states,and Lang[Lang (2018)] proposed a SQPC protocol using single photons.Ye et al.[Ye and Ye (2018)] designed a multi-user SQPC protocol based on two-particle product states.Moreover,two classical participants need to prepare a shared key before work in the SQPC protocols [Thapliyala,Sharmab and Pathak (2016);Lang (2018);Ye and Ye (2018)].
Traditionally,it is assumed that a classical party can only perform a restricted set of classical operations over a quantum channel.Specifically,a classical party can measure a qubit in the classical basisand reflect a qubit back without disturbance.Furthermore,the classical user does not require quantum memory.In the paper,we propose a two-party semi-quantum private comparison protocol based on GHZ states.There are three participants in the protocol,where server has all quantum powers,but Alice and Bob are classical.Alice and Bob compare the equality of their private secret with the help of server.Furthermore,server is semi-honest which means that he will follow the protocol honestly,but he may try to learn additional information from the protocol execution.
The rest of this paper is outlined as follows.In the next section,we give the description of the two-party semi-quantum private comparison protocol in detail.Section 3,we demonstrate the security and efficiency of our protocol.Finally,a conclusion is given in Section 4.
2 Protocol for two-party semi-quantum private comparison
In this section,we propose a two-party semi-quantum private comparison scheme.There are three participants in the protocol Alice,Bob and server.Alice and Bob are classic.They want to compare the equality of their private secret.Server is a semi-honest third party who may try to disclose the secret key during executing of the protocol,but he cannot public a fake result or collude with the participants.
Before giving our scheme,we first describe three-particle GHZ states which will be used in our protocol.
The three-particle GHZ states can be denoted as
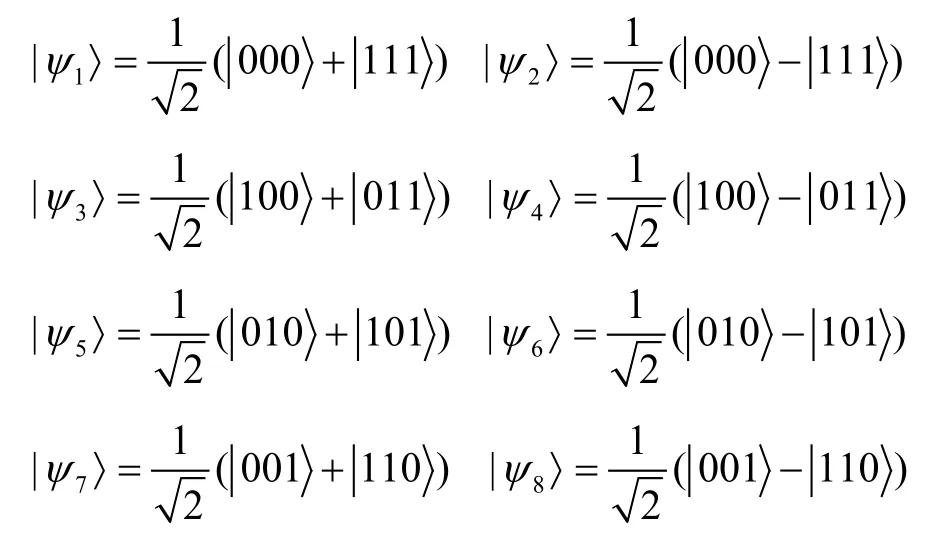
It is assumed in the proposed protocol that the quantum channels is ideal (i.e.,non-lossy and noiseless)and an authenticated classical channel is shared among all the legitimate participants.An adversary can eavesdrop a message communicated through this channel.Based on the scenario described above,the process of the proposed scheme will be described in steps as follows.
Step 1:Server prepares4nGHZ states,each of whichiswherei= 1 to 8.He extracts allthefirst particlesin the GHZ states,and formsa sequenceS1inorder.The second particles form a sequenceS2in order,and the third particles form a sequenceS3in order.
Server keeps the sequenceS1,sendsS2to Alice andS3to Bob.S1,S2andS3containN=4nqubits.
Step 2:Upon receiving the particles from server,Alice and Bob can perform one of the following operations (Measure or Reflect).
Measure:Measures the particle in the classical basisand saves the measurement results.
Reflect:Reflects the qubits back without disturbance.
Step 3:eavesdropping checking Server restores the returning qubits.Alice and Bob announce their operations on all qubits.In the same position ofS2andS3,only one of them perform a measurement,they need to announce the measurement result.If both of them perform a measurement,they must keep the measurement results confidential.
Based on the announcement of Alice and Bob,server begins to detect eavesdropping.If both Alice and Bob reflect the qubits,server will perform a GHZ measurement on the reflected particles with his own one (i.e.,the original entangled GHZ state).In other word,if one of them measures the qubit,server will measure his own particle and the reflected particle in the classical basis.Finally,server checks his measurement results,if the error rate exceeds a pre-defined threshold,they proceed to the next step,otherwise terminate the protocol.
Step 4:After ensuring that there is no eavesdropping,Alice and Bob discard the decoy photons.For the remaining qubits,Alice and Bob perform a measurement in the same positon ofS2andS3.They can use them measurement resultsrAandrB(each of n bit length)to compare their private secret.
To ensure that Alice and Bob secretly compare their information without exposing their actual contents,Alice and Bob employ the one-way hash function [Damgard (1990)](i.e.,h():{0,1}m→{0,1}n,where m denotes the length of the inputted data,and n denotes the length of the hash code)on their binary representation of secret messageMAandMBto obtain two hash codesh(MA)andh(MB),each of n bit length.Finally,they compute theRA=rA⊕h(MA)andRB=rB⊕h(MB).Finally,Alice and Bob publishRAandRBto server,whereRAandRBcontain n bit.
Step 5:Server generates a classical bit stringCof n-bits corresponding to the choice of the initial GHZ states,for the ith GHZ state beinghe generatesith bit value inCas 0 (1).Server computesR,which is now exclusive-OR result ofRA,RBandCasR=C⊕RA⊕RB.The bit value 0 (1)ofRicorresponds to the same (different)values ofandThus,if server found out thatRi=0for all,he will public 0,otherwise public 1.
The process of the proposed protocol is shown in Fig.1,and Tab.1 demonstrates the detailed process,where the parameters “M” and “R” denote measurement and reflection,“GHZ” denotes GHZ measurement.
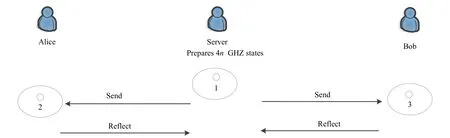
Figure1:The process of the proposed protocol
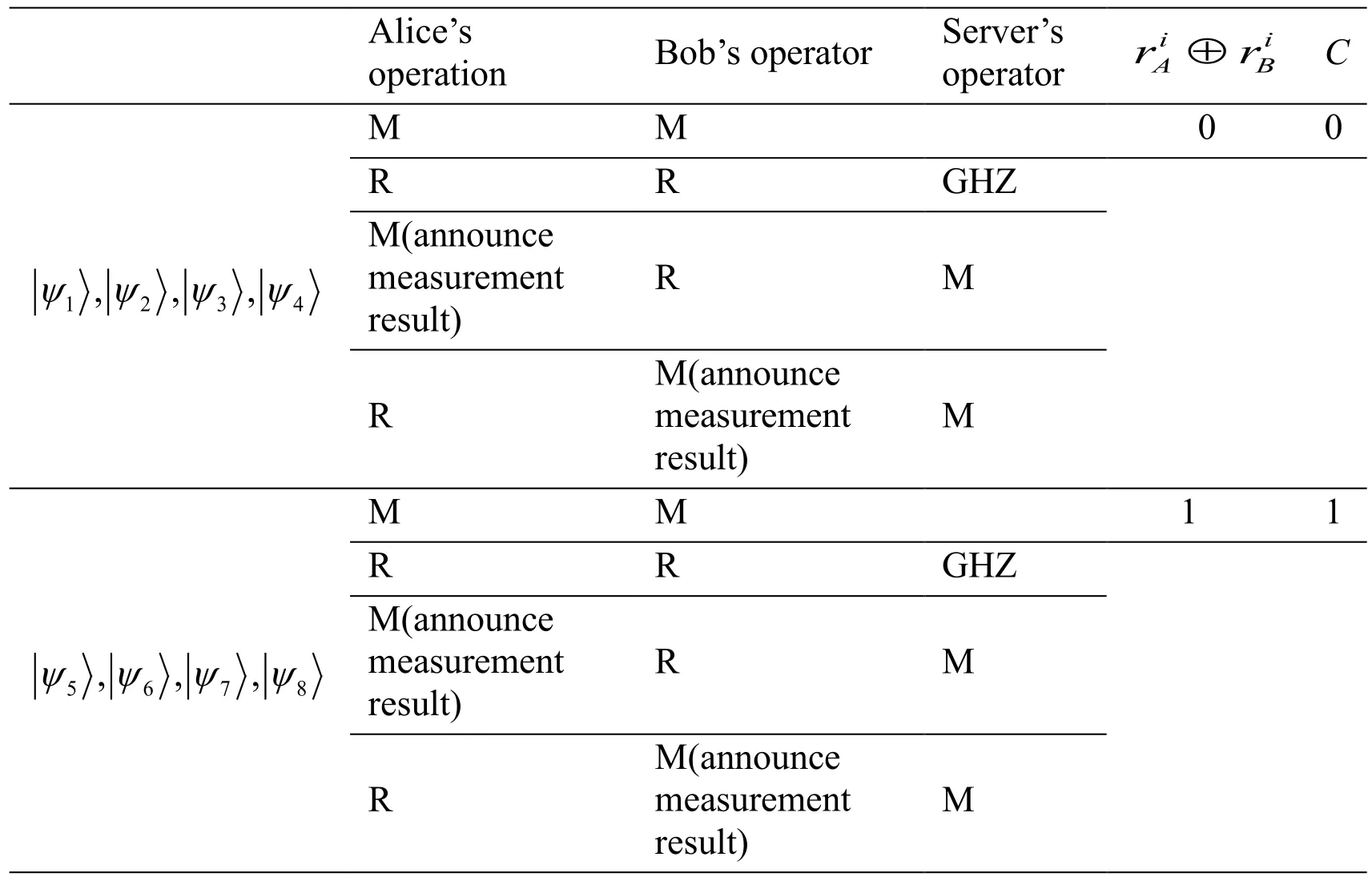
Table1:The detailed process of the proposed protocol
Here it is important to note that Alice and Bob cannot announce the measurement results when both of them perform measurement operation in the same position.
3 Security and efficiency analysis
In this section,we first analyze the security of the eavesdropping detection to show that the proposed protocol can avoid the outside attacks.Therefore,the efficiency of the protocol is analyzed.
3.1 The detection probability of eavesdropping information
Now,let us analyze the efficiency of the eavesdropping detection in the proposed protocol.If there is an outside eavesdropper (Eve)who attempts to derive the session key.She can only use the chance of the transmission ofS2andS3to steal qubits,Eve performs the unitary attack operationon the composed system firstly,and then Alice,Bob and server perform the corresponding operation on these qubits.All the transmitted particles are sent together before eavesdropping is detected.Because Eve does not know which particles are used to detect eavesdropping,she can only perform the same attack operation on all the particles.As for Eve,the state of qubits is distinguishable from the complete mixture,so all qubits are considered in either of the states |0> or |1> with an equal probabilityp=0.5.
Generally speaking,suppose there is a group of decoy photons in GHZ states |ψ1〉.And we assume that after the attack operationis performed,the state |0> and |1> become

where |xi>and |yi>are the pure ancillary states determined byuniquely,and

Then let us compute the detection probability.After attacked by Eve,the state of the composed system becomes
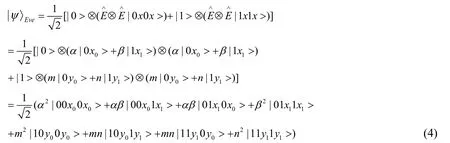
Obviously,when Alice,Bob and server perform measurement on the decoy photons,the probability without an eavesdropper is

So the lower bound of the detection probability is

Suppose |α|2=aand |n|2=b,whereaandbare positive real numbers,anda=b= 1.
Then
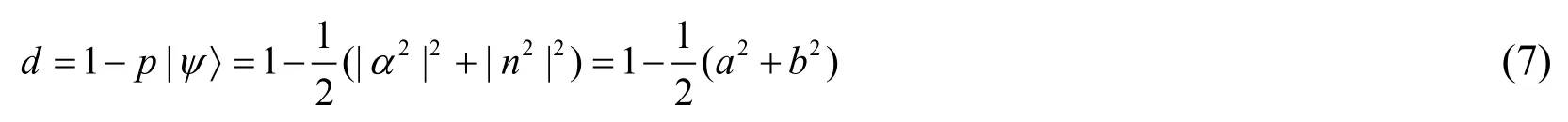
In the case ofp0=p1=0.5,the maximal amount of information is equal to the Shannon entropy of a binary channel [Gisin,Ribordy and Tittel et al.(2002)],

After some simple mathematical calculations,we can get

The maximumIis

The above results show that if Eve wants to obtain the full information (I=1),the probabilities of the eavesdropping detection isd=0.75.When Eve gains the information,the detection probability is shown in Fig.2.
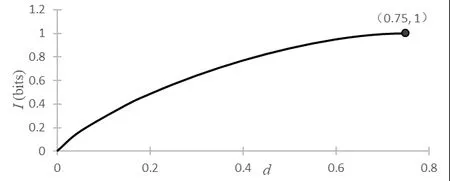
Figure2:Detection probability of eavesdropping information
3.2 Intercept-measure-resend attack
In the proposed protocol,Alice and Bob randomly perform measurement and reflected operation.Without knowing the position of these operation,Eve will be detected inevitably if Eve performs a projective measurement on them.
Supposed server prepares Bell statesand send the first and second photon to Alice and Bob,respectively.If Eve intercepts this qubit and performs a measurement on it in the basiswill collapsed intoEve retransmits this result state to Alice and Bob.Accordingly the protocol,Alice and Bob choose randomly either Measurement or Reflected.If one of Alice and Bob decides to Measurement,Eve induces no error.In view ofif both Alice and Bob decide to Reflected,server performs GHZ basis measurement and obtainsoreach with probability of 1/2.Thus,the error rate introduced by Eve is 50%.Therefore,the probability for Eve to pass the security checking isAnd Eve only can obtain the valuable information when both Alice and Bob perform measurement operation,the probability is 1/4.Thus,the probability for Eve to pass the security checking and obtain the valuable information isfor Eve’s interceptmeasure-resend attack,the probability of being detected isThis probability is approximate to 1,ifnis large enough.
3.3 Flip attack
When the sequenceS2andS3are transmitted from server to Alice and Bob,Eve can cause Alice and Bob to obtain the wrong bit value of the message by flipping some particles in the sequence.Suppose server prepares GHZ statesand sends the first and second photon to Alice and Bob respectively.Eve intercepts and flips the qubit.Accordingly the protocol,Alice and Bob choose randomly either measurement or reflected operation.If both Alice and Bob decide to measure,Eve induces no error.If one of them decides to reflect,server can find the flip attack with the help of the announcement of Alice and Bob.Thus,the error rate introduced by Eve is 100%.
Therefore,the probability for Eve to pass the security checking is.Thus,fornencoded message qubits,the probability of being detected isWith the increase ofn,the probability of Eve being detected is also increasing.
3.4 Man-in-the-middle attack
If Eve captures the qubit from server to Alice and Bob.She prepares another Bell statesends them to Alice and Bob.Then Eve also catches that qubits back to server.Because we just send back the reflected qubits,and the order of the reflected particle sequence is completely secret to Eve.Even if Eve catches these qubits,she also cannot obtain any secret information.
3.5 Trojan horse attack
Since the proposed protocol is a two-way communication protocol,Eve may implement a Trojan horse attack to get the secret message.In order to resist the attack,a photon number splitter (PNS)and a wavelength filter could be added before Alice and Bob’s devices [Cai (2006);Li,Deng and Zhou (2006);Deng,Li,Zhou et al.(2005)].
3.6 Server’s attack
Our proposed protocol is considered in semi-honest model.Server may try to learn additional information from the protocol execution.In the protocol,server knows the state of GHZ states and Alice and Bob’s operations on each qubit.From these information,server can only correctly obtain Alice and Bob’s measurement results with probabilityIf the length of the secret message isn,server will have a probability ofto get secret message.When the length of the secret message is large enough,the probability that server correctly obtains Alice and Bob’s secret message is negligible.Thus,the protocol is unconditionally secure against the server.
3.7 Efficiency analysis
Performance of a quantum protocol can be characterized using qubit efficiency [Cabello(2000)],wherecis the number of secret bits received by the legal receiver,qdenotes the number of transmitted qubits,andbis the number of classical bits for decoding of the message (classical communications used for checking of eavesdropping are not counted).In our protocol,in order to make the Alice and Bob obtainnbits message,server should prepare 4nGHZ states photons and send 4nphotons to Alice and Bob,respectively.Then Alice and Bob reflect 2nphotons back to server.In addition,2nclassical bits are needed for Alice and Bob to inform server their operations on photons,nclassical bits are needed for Alice and Bob to publicRAandRB.Therefore,totalq=4n+4n+2n+2n= 12n,b=2n+n+n+n= 5n,c=n.Thus the efficiency of the proposed protocol would bewhich is 5.88%.
4 Conclusion
In the paper,a two-party semi-quantum private comparison scheme is proposed based on GHZ states.In the protocol,Alice and Bob are classical,they are restricted to either measuring a quantum state or reflecting it in the classical basisCompared with the previous SQPC protocols,the advantage of our protocol lies in that the classical participants only send the reflected qubits back to server,it avoids measurement results leakage,and it also does not need the pre-shared key and quantum entanglement swapping.According to the security analysis,the protocol can resist the outside attacks and semi-honest server attack.It can be used to solve a real application problems,because end users are expected to be classical in reality.Therefore,our proposed protocol is more practical and feasible with current technique.
Acknowledgement:The work was supported by the National Natural Science Foundation of China (Grant No.61572086),Major Project of Education Department in Sichuan (Grant No.18ZA0109),and Web Culture Project Sponsored by the Humanities and Social Science Research Base of the Sichuan Provincial Education Department(Grant No.WLWH18-22).
 Computers Materials&Continua2019年11期
Computers Materials&Continua2019年11期
- Computers Materials&Continua的其它文章
- Efficient Computation Offloading in Mobile Cloud Computing for Video Streaming Over 5G
- Geek Talents:Who are the Top Experts on GitHub and Stack Overflow?
- Implementing the Node Based Smoothed Finite Element Method as User Element in Abaqus for Linear and Nonlinear Elasticity
- Dynamics of the Moving Ring Load Acting in the System“Hollow Cylinder + Surrounding Medium” with Inhomogeneous Initial Stresses
- Human Behavior Classification Using Geometrical Features of Skeleton and Support Vector Machines
- Improvement of Flat Surfaces Quality of Aluminum Alloy 6061-O By A Proposed Trajectory of Ball Burnishing Tool
